C++ Bubble Sort Algorithm

Introduction to Bubble Sort Algorithm

In the bubble sort technique, the largest element is placed in its proper place in the list at the end of each iteration. In other words, the largest element in the list bubbles up.

The main disadvantage of this algorithm is that the performance of bubble sort is not suitable for large data sets.

The average and worst-case complexity of Bubble sort is $O(n^2)$, where n is the number of elements in the Array.

Below is the algorithm for the bubble sort algorithm, where we traverse the list using two iterative loops.

In the outer loop, we start iterating from the first element (0th index), while in the inner loop, we start from the adjacent element. We compare the adjacent elements in the inner loop and swap them if they are not in order. At the end of each outer loop iteration, the largest element bubbles up to the end of the array.

Working of Bubble sort Algorithm

Let's take an unsorted array to understand the working of the bubble sort algorithm.

The elements of the array are: [12, 7, 20, 1, 14].

First Pass:

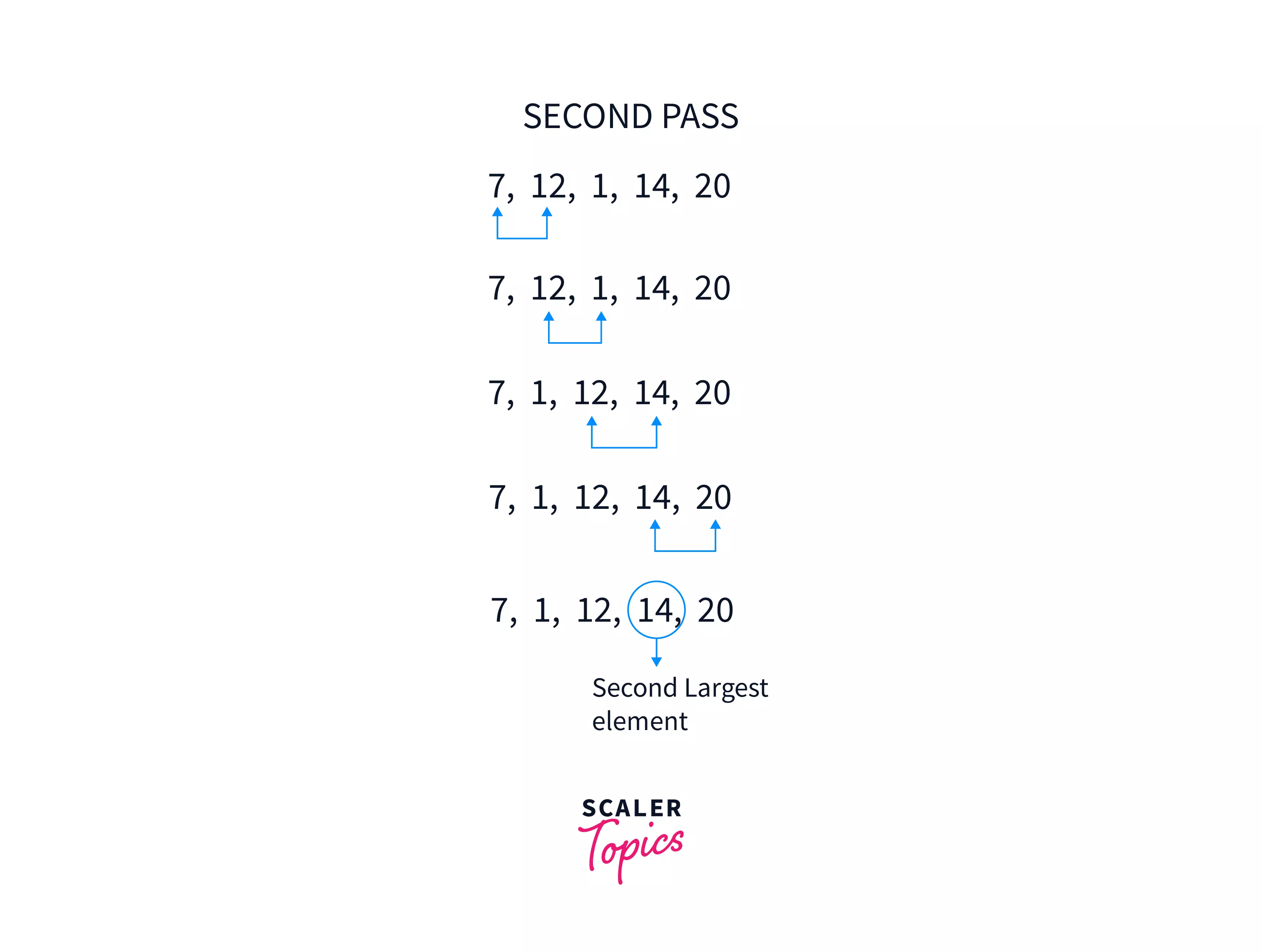
Second Pass:

Third Pass:

As shown in the above illustration, the largest element bubbles up to the last, thus sorting the array. Each element is compared to its adjacent element in every pass and swapped if not in order.

Since we are sorting the array in ascending order, at the end of the first pass, the largest element is placed at the end of the array. For the second pass, the second largest element is placed at the second last position in the list, and so on.

Implementation of Bubble Sort in C++

Output

In the above implementation of Bubble Sort in the C++ program, we initialized an array arr containing 5 elements in the main function. We then sorted it using the bubble sort algorithm implemented in the bubbleSort function.

In the bubbleSort function, we used two for loops to iterate through the adjacent elements of the array. At the end of each iteration of the outer loop, the largest element in the array is bubbled up to the end of the array. Thus after repeating these steps, the final result is a sorted array.

Bubble Sort Complexity

• Time Complexity

  In this sorting algorithm, (N-1) comparisons are made in the first pass, (N-2) comparisons in the second pass, and so on. Hence the total number of comparisons in bubble sort is calculated as:

  Let us now discuss the best case, average case, and worst case time complexity of bubble sort.

  • Best Case - Irrespective of whether the array is sorted fully or partially or not at all, Bubble Sort takes O(n^2) comparisons. Hence, the best-case time complexity is $O(n^2)$.
  • Average Case - This occurs when elements in the array are in some random order, i.e., neither ascending nor descending. Hence the average case time complexity is $O(n^2)$.
  • Worst Case - This occurs when the array to be sorted has elements in reverse order. Hence worst, the case time complexity is $O(n^2)$.

• Space Complexity

  The Bubble Sort algorithm requires only one additional memory space to create a temp variable to implement the swapping of elements. Therefore, the auxiliary space complexity for the bubble sort algorithm is O(1).

Optimized Bubble Sort Algorithm

In the traditional bubble sort technique, we make comparisons even if the elements in the array are sorted, which as a result, increases the execution time of the algorithm.

So, to get rid of this problem, we create an extra variable, isSwap, and set it to True if swapping is required. Else False.

The above change can be really helpful, as if no swapping is required in the current iteration, we can set isSwap to False, which means that the array is already sorted. No further iterations are required, so we can break the loop and stop the program's execution, thus reducing the execution time.

Algorithm for Optimized Bubble Sort

The above algorithm will optimize the bubble sort technique by reducing its execution time.

Optimized Bubble Sort Complexity

• Time Complexity

  Let us discuss the best case, average case, and worst case time complexity of bubble sort.

  • Best Case - If the array is already sorted, after the 1st operation, when we would have done O(N) operations, swapped will remain false, and we will not process the 2nd iteration. Hence, the best-case time complexity is $O(n)$.
  • Average Case - This occurs when elements in the array are in some random order, i.e., neither ascending nor descending. Hence the average case time complexity is $O(n^2)$.
  • Worst Case - This occurs when the array to be sorted has elements in reverse order. Hence worst, the case time complexity is $O(n^2)$.

• Space Complexity

  The Bubble Sort algorithm requires two additional variables, first, to create a temp variable(Here we have used std::swap function, but internally it uses a temporary variable), and second, a boolean variable swapped. Therefore, the auxiliary space complexity for the bubble sort algorithm is O(1).

Characteristics of Bubble Sort

1. In-place Sorting - Bubble sort is an in-place sorting algorithm because it does not require any auxiliary space to perform the sorting. However, a small amount of extra storage space is allowed for auxiliary variables.

2. Stable - Bubble sort is a stable sorting algorithm because two elements with equal values appear in the same order in the sorted array output as in the input array.

3. Boundary Cases - Bubble sort takes up a minimum time of order of n (i.e., linear) when elements in the array are already sorted.

4. When is bubble sort used -

   • when we are not concerned about the time complexity of the program
   • when we want the program to be short and simple to understand.