Container with Most Water

Problem Statement

You are given an array $height[n]$ of integers of size n, where each value represents a coordinate position $(i, height[i])$. n vertical lines are drawn such that the endpoints of line i are at $(i, 0)$ and $(i, height[i])$. Find the container that is formed by two lines along with the x-axis, where the container contains the most water.

Example

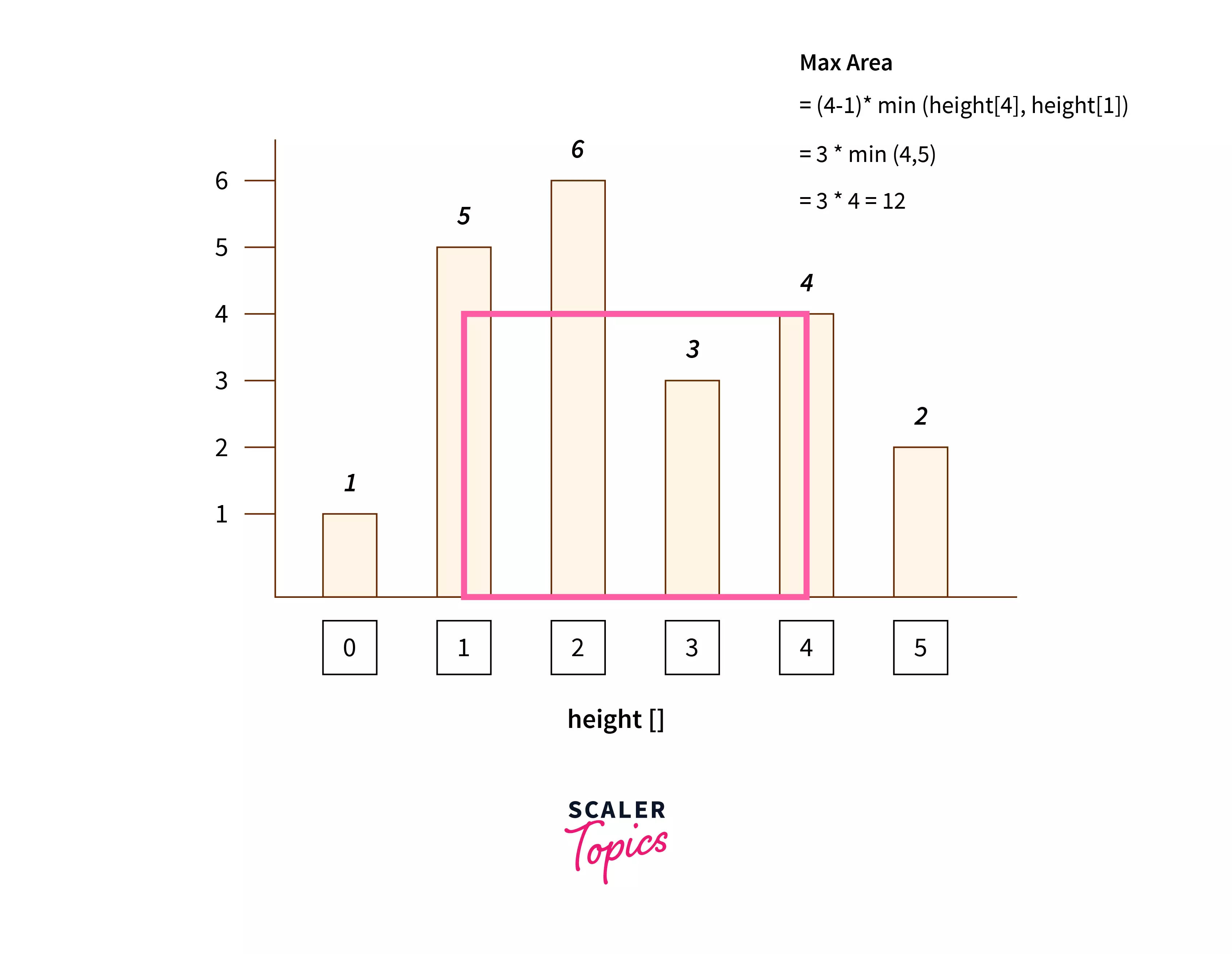
Input - 1

Output - 1

Explanation

The area shown in the blue section is the maximum area.

• 1 and 4 are distance 3 apart.
• Therefore, the size of the base = 3.
• Height of the container will be a minimum of $(5, 4)$ $= 4$
• Hence, The total area becomes $3 * 4$ $= 12$ units.

Input - 2

Output - 2

Explanation

Since there are only two endpoints, the area becomes $1 * 1$ $= 1$.

Constraints

Algorithm - 1 : Naive Approach - Using Nested Loops

Intuition

The most basic and straightforward approach for a container with the most water is to check all the possible pairs of boundaries and find out a team that has a maximum area.

Algorithm

1. Initialize a variable maxArea to track the current maximum area.
2. Run a nested loop, the outer loop from $i = 0$ to end $(n-1)$.
3. While the inner loop runs from $i+1$ to end $(n-1)$ with loop counter j.
4. Find the area for every pair of boundaries i and j, and store the area in the variable maxArea, where maxArea= $(j -i)$*$min(height[i], height[j])$. Update the variable maxArea, if the current area is greater than the maxArea.
5. Return the maxArea.

Code Implementation

Code in C++ :

Code in Java :

Code in Python :

Output :

Time Complexity :
The time complexity is $O(n^2)$. Since two nested loops traverse the array.

Space Complexity :
The space complexity is $O(1)$. Since no extra space is used in the solution of the container with the most water.

Algorithm - 2 : Efficient Approach - Using Two Pointers

Intuition

We take two pointers, one at the start and one at the end of the array, and we keep track of the maximum area between the lines in a variable maxArea. At each step, we calculate the area formed by the two pointers, update the maximum area, and move the pointer pointing to the shorter line by one to the opposite end.

Check the below illustration of two pointer approach to solving container with most water problem :

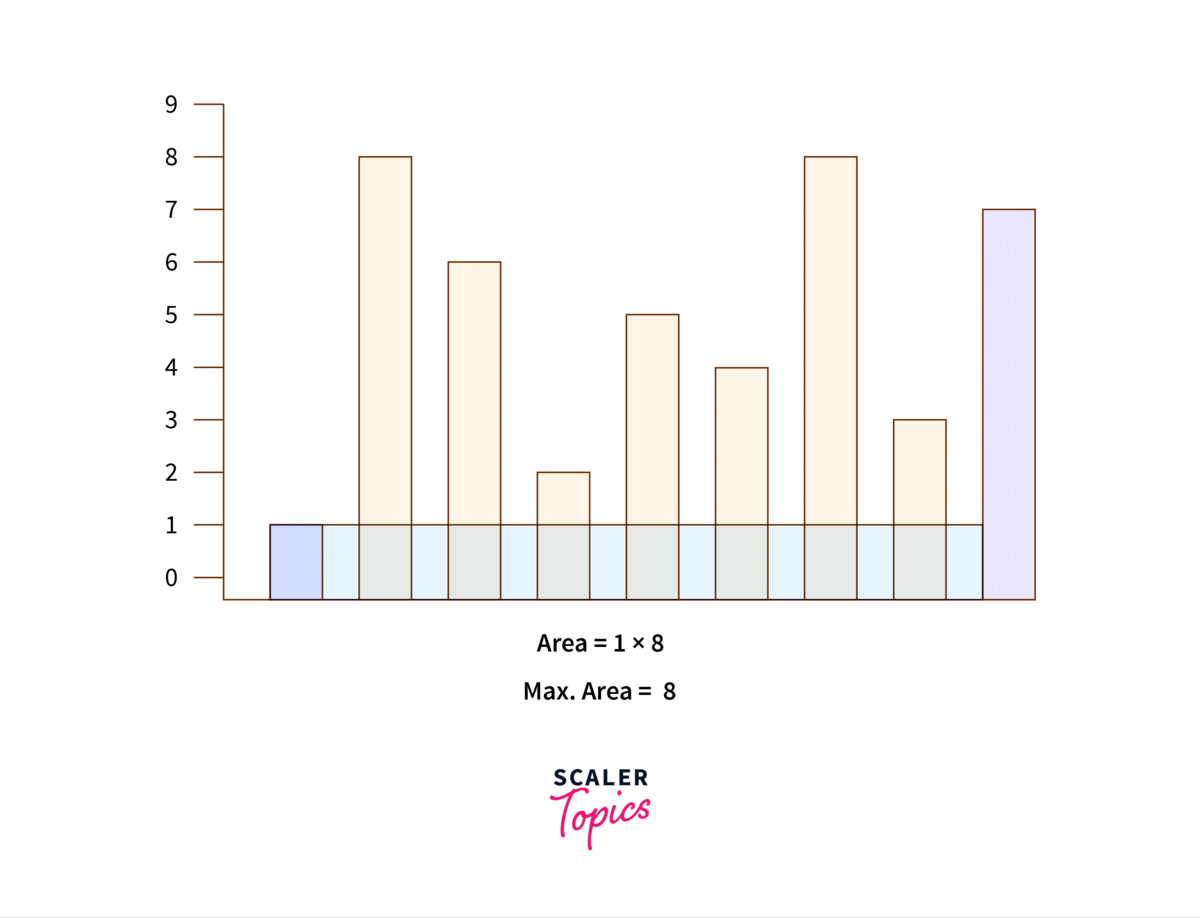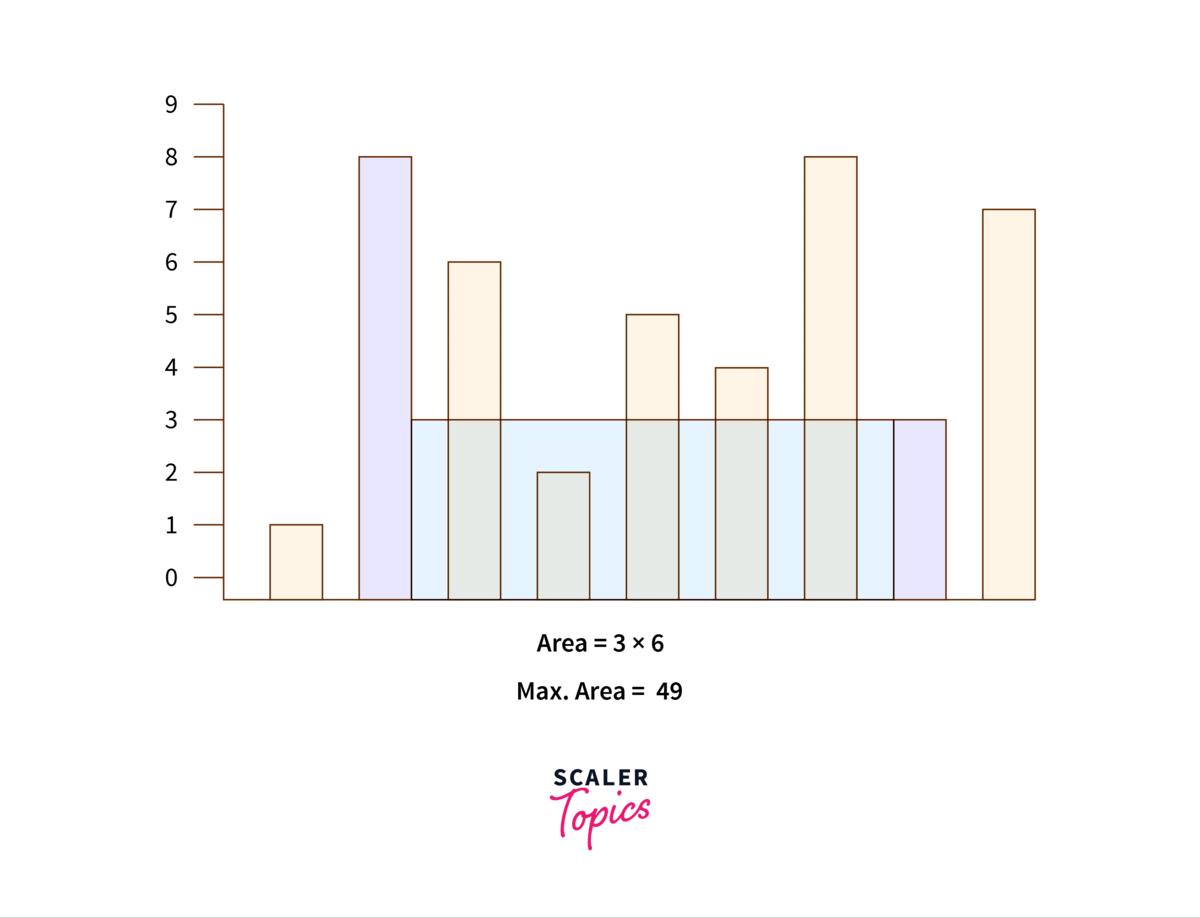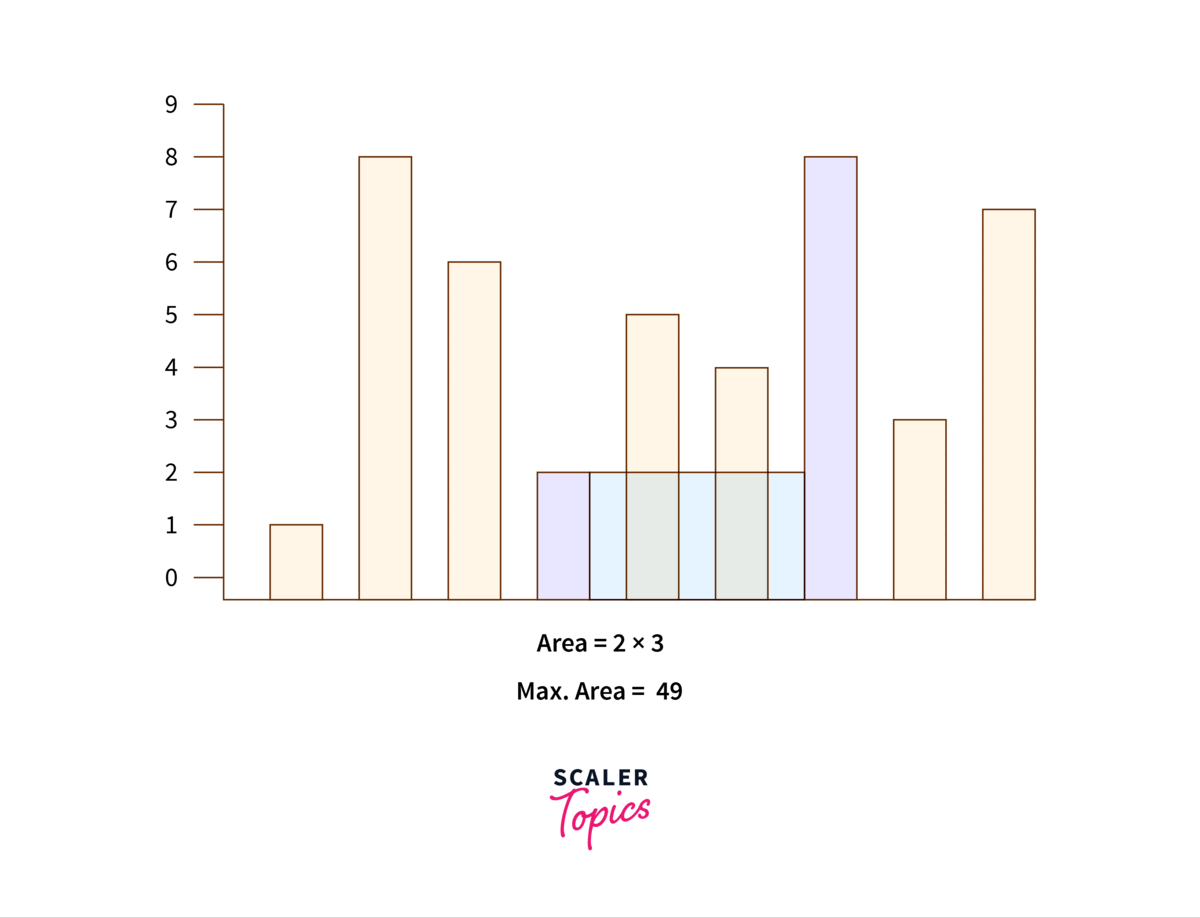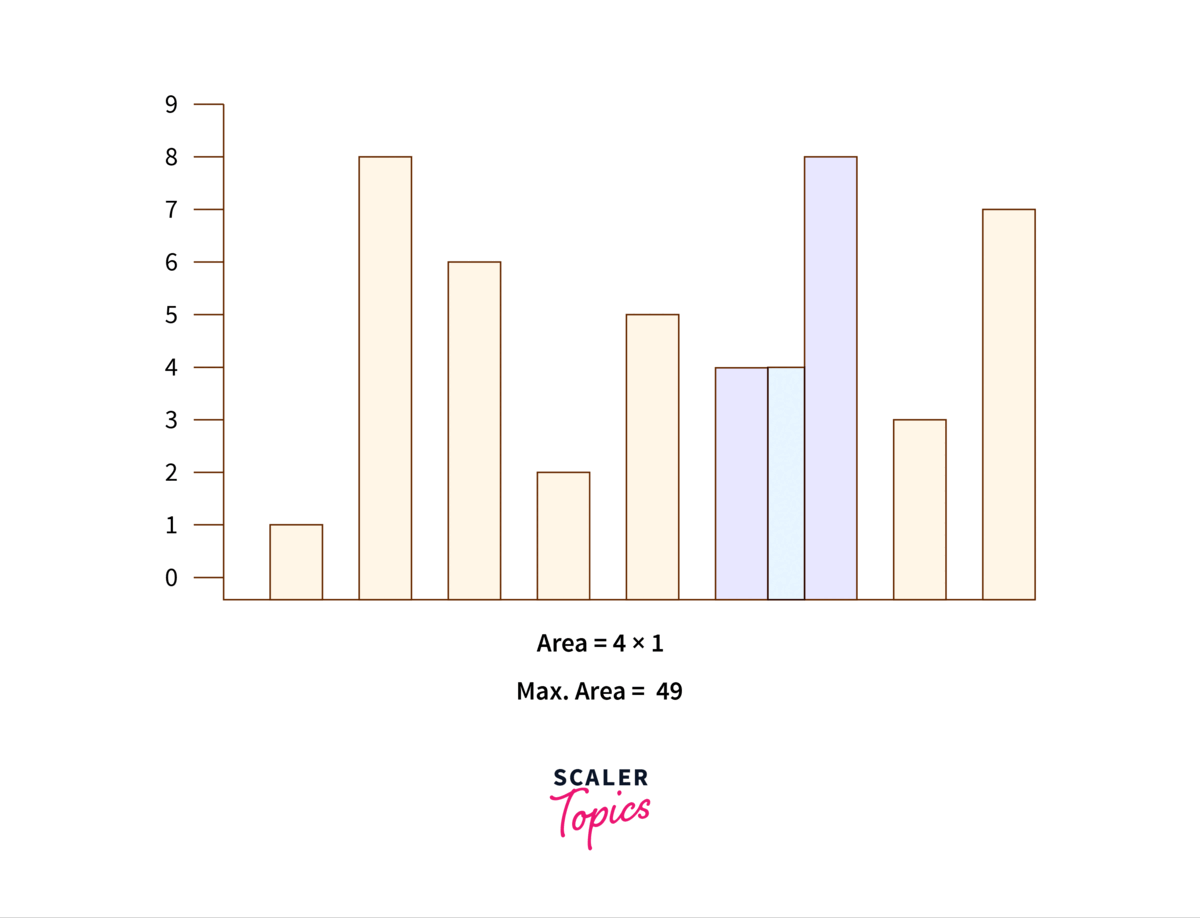
Algorithm

1. Initialize a variable maxArea to track the current maximum area of a container with the most water.
2. Keep two indices, $i$ and $j$ initialized at 0 and $n-1$, respectively.
3. Run a loop until the left index i is less than the right index j.
4. Calculate the area formed between indices i and j, where area $= Math.min(height[i], height[j]) * (j - i))$ and update the maxArea.
5. If the value at $height[i]$ is lesser than $height[j]$ then move index i by one right. Else move index j by one left.
6. Return the maxArea.

Code Implementation

Code in C++ :

Code in Java :

Code in Python :

Output :

Time Complexity :
The time complexity is $O(n)$. Since only one traversal of the array is required.

Space Complexity :
The space complexity is $O(1)$. Since no extra space is used in the solution of the container with the most water.