Binary Representation of A Given Number in C++

Binary Numbers are represented by two digits, 0 (zero) and 1 (one). Binary numbers are represented in the base-2 numeral system. Every digit in the binary system is called a bit. Decimal numbers refer to the base-10 numbering system.

Generally, a decimal can be anything based on the number 10. In C++, we can convert a decimal number to a binary number using the Iterative method or recursive method. We can also do it using Bitwise Operator, and Bitset class.

C++ program to convert Decimal Number to Binary Number

We will discuss two methods to convert from decimal two binary.

Let us discuss the Binary Representation of a number:

Iterative Method

Algorithm: Let us take a temporary variable named binarynumber which would help us to store the binary representation of the decimal number. Also, let us take another variable, i, which would help us to move the digit to the appropriate place value.

Step 1: Initialize the values binarynumber = 0, i = 1;
Step 2: Use the modulus operator % to get the remainder of the given decimal number by 2. We perform modulo to get the least significant bit (lsb)
Step 3: Use the division operator / to divide the number by 2. We perform this step to get the next least significant bit (2nd lsb)
Step 4: Compute binarynumber += remainder * i; this step helps us to store the computed binary numbers till the time here we are multiplying remainder * i to achieve the place value
Step 5: Multiple the value of i by 10; this step is essential as it increases the place value of the binary number
Step 6: Repeat the above steps until the given decimal number becomes zero.

Let's see the implementation of the above algorithm:

Output:

Explanation for the above Implementation

• In the above program, we have taken a decimal number, n=11, and we used a while loop to iterate over the decimal number to get the Binary Representation of a number. The while loop in C++ will terminate when n becomes 0 (zero).
• In the while loop, we store the remainder of the given decimal number by computing n%2, we update the binary number by computing binarynumber += remainder* i, for every turn of this step place value increases as we are multiplying the remainder with i, please note that we multiply i value with 10 ($i=i*10$) for every iteration to increase the place value.

Recursive Method

Algorithm:

Create a function that lets its name be bintodec. It is for converting the decimal number to a binary number.

Step 1: From the main function, call bintodec function with a passing decimal number as an argument.
Step 2: recursively call bintodec function by dividing the number by2 while the parameter/current number is greater than 1.

Step 4: In the bintodec function, print the binary representation of a number by performing a modulo operation with 2 on the decimal number

Let’s see the implementation of the above algorithm:

Output:

Explanation for the above Implementation

• In the above program, we have taken a decimal number n=13, and we have also created a bintodec function for converting the given decimal number to a binary number
• We call the bintodec function from the main function. In the bintodec function, we are checking whether the decimal number is greater than 1. If it is greater than 1, then we call the bintodec function by dividing the decimal number by 2. Once the if condition becomes false, we start printing the binary representation of a number by performing a modulo operation on the decimal number by 2.

C++ Program to Convert Decimal to Binary Using Bitwise Operator in Recursive Mode

• Binary operators can convert a given decimal number to a binary number.
  • Binary Shift Right Operator (>>) takes two operands, say x and y, where x denotes the actual integer while y denotes the number of places to shift
  • For example, x>>y means shifting the bits of x by y positions towards the right, or we can remove the last y bits which are equivalent to dividing x by 2 to the power y.
  • For example, say n = 14, the binary format is 1110. By performing the operation, n >> 2, we remove the last two bits from n. So we get 11 or in decimal format 3.

Let us see how we could convert a decimal number to a binary number using a bitwise operator.

Algorithm

Step 1: Execution starts from the main function; we have taken a decimal number and passed this decimal number to the convert function.
Step 2: Repeat step 3 while the decimal number is greater than 1.
Step 3: Call the convert function by performing a right shift on the decimal number to gain the place value.
Step 4: In the convert function, we print the binary number by computing the decimal number with Bitwise AND operator.

Let us see the implementation of the above approach

Output:

Explanation for the above Implementation

In the above code, we have taken the number 13, passing this number to a convert function which helps us convert decimal format to binary format. In the convert function, we check if the number is greater than 1 or not. If it is greater than 1, then we again call the convert function by performing the right shift on the decimal number. When the decimal number is not greater than 1, we print the least significant bit of the number by computing the Bitwise AND using Bitwise AND operator & to check if the last bit is 1 or 0.

Using Bitset Class of C++ to Convert Decimal Number to Binary Number

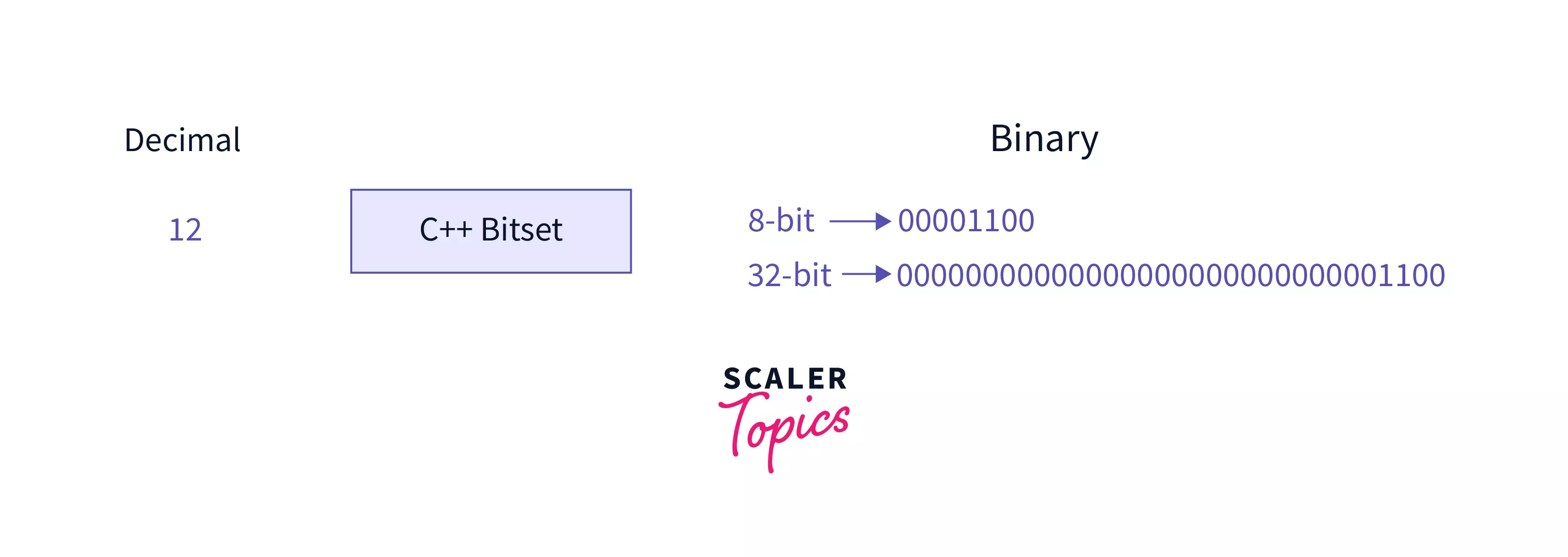
Bitset class in C++ stores only boolean values 0, 1, i.e., true or false. Bitset class stores the negative integers as well as the positive integers. The major advantage of the Bitset class is that it allows us to store the binary representation of a given decimal number in 8-bit, 32-bit, or an n-bit representation, which is to be defined while writing the program. In the bitset class, each bit can be accessed individually with the help of the array indexing operator. Indexing in the Bitset class starts from backwards with 0 as the right-most digit index. The bitset size is fixed at the compile time itself, so it cannot be changed during runtime.

Implementation of Bitset Class

Output:

Explanation for the above Implementation

In the above code, execution starts from the main function, and we have taken two variables, num1 and num2, with the values 10 and 21, respectively.

• bitset<8> denotes the decimal number in 8-bit binary format.
• bitset<32> denotes the decimal number in 32-bit binary format.

C++ Program to Convert Binary Numbers to Decimal Numbers

Until now, we have seen how to convert a number from decimal to binary. Now let us look at converting a given number from binary format to a decimal format.

Algorithm:

Let us take a variable named bin to store the binary number and another variable as number to store the computed decimal number.

Step 1: Initialize the number variable with zero.
Step 2: Store the remainder by computing bin%10; we perform this step to get the equivalent decimal number for the binary number.
Step 3: Use the division operator and divide the binary number by 10; this step helps compute the next least significant bit.
Step 4: We compute number += rem * pow(2, i) to get the decimal number and store it in the number variable.
Step 5: Increment the value of i to increase the place value of the decimal number.

Implementation of the above approach:

Output:

Explanation for the above Implementation

Let us understand the process of converting a number from Binary to Decimal. We perform the modulo operation on the input number to extract the right-most binary digit of it; then, we multiply them by their place values in the base2 number system starting from zero. Then we add all the multiplied values to get its equivalent decimal number.