C++ Recursion

Syntax of Recursive Function

The syntax of a general recursion function is shown below,

Working of Recursion

Using recursion, it is possible to solve a complex problem with very few lines of code, dividing the input of the problem statement with each function call until finally stopping to return/provide the combined solution. Let us discuss the working of recursion in C++. Initially program calls a particular function, and then subsequently that function calls itself, again and again. When this process gets interrupted due to some terminating base condition, the return statement of the function (the most recently called) gets executed and returns the appropriate value. Finally, the remaining lines of code for the last called function gets executed followed by the return statement. This procedure continues until the flow of the program reaches the particular function that has initiated the call. The example given below will make this description clear.

Output:

Explanation:

• As we all know the program starts from the main function, so printNumbers(6) will be called first.
• Inside the printNumbers(6), condition of if block will be evaluated as false hence, printNumbers(5) will be called, and so on. This process will be repeated till the call of printNumbers(0).
• Now, the condition inside if block will be evaluated to true. Hence invocation of printNumbers(0) will finish execution with a void return value.
• After then the control will go to printNumbers(1) and the remaining lines of code will get executed. Hence, 1 will be printed.
• This process will continue until the execution of the last line of code for the invocation of printNumbers(6).

Diagramatic Representation of Recursion

The entire recursion flow starts from the first function call and then stops at some condition followed by the return statement.

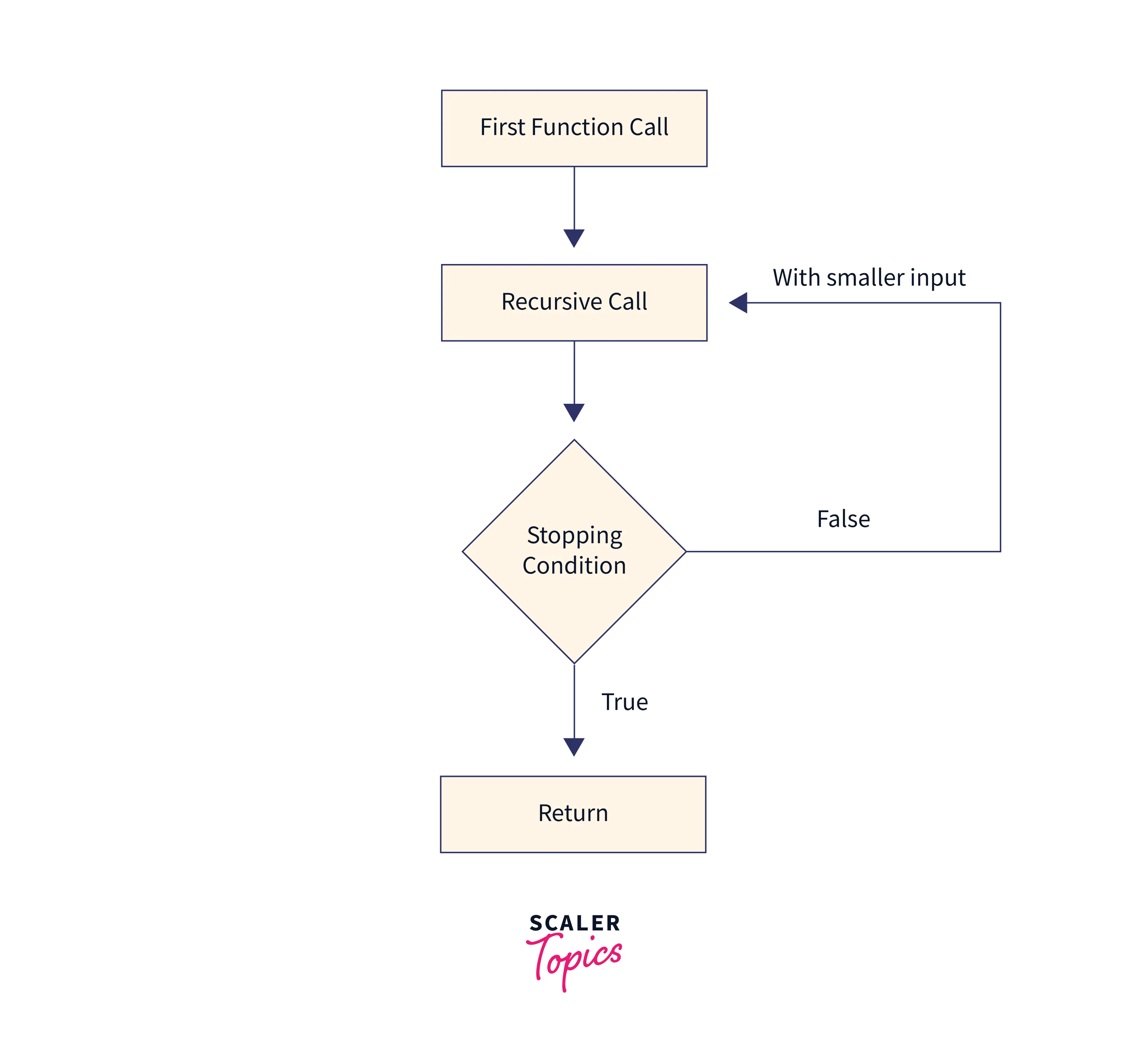
What is a Base Condition in Recursion?

Till now, you might have got an idea about what recursion is. It is just a function calling itself again and again. Have you wondered when the function will stop calling itself? There must be some endpoint, otherwise our program will get stuck in the infinite loop. So the condition which is written inside the recursive function definition to stop the recursive calls is called the base condition. It is responsible to avoid the infinite loop in recursive functions.

Memory Allocation for the Recursive Call

In C++, there exists a concept of the function call stack, which is responsible for the maintenance and storage of all variables according to the code execution of the function. The element of the call stack includes automatic variables, activation record/local variables of a function, return location, etc. If there are multiple nested calls, the functions are pushed into the stack in the same order as they were called, and after successful execution, the function gets popped out from the stack by providing the return value to the next top function in the call stack. The diagram shown below will make these things clear.

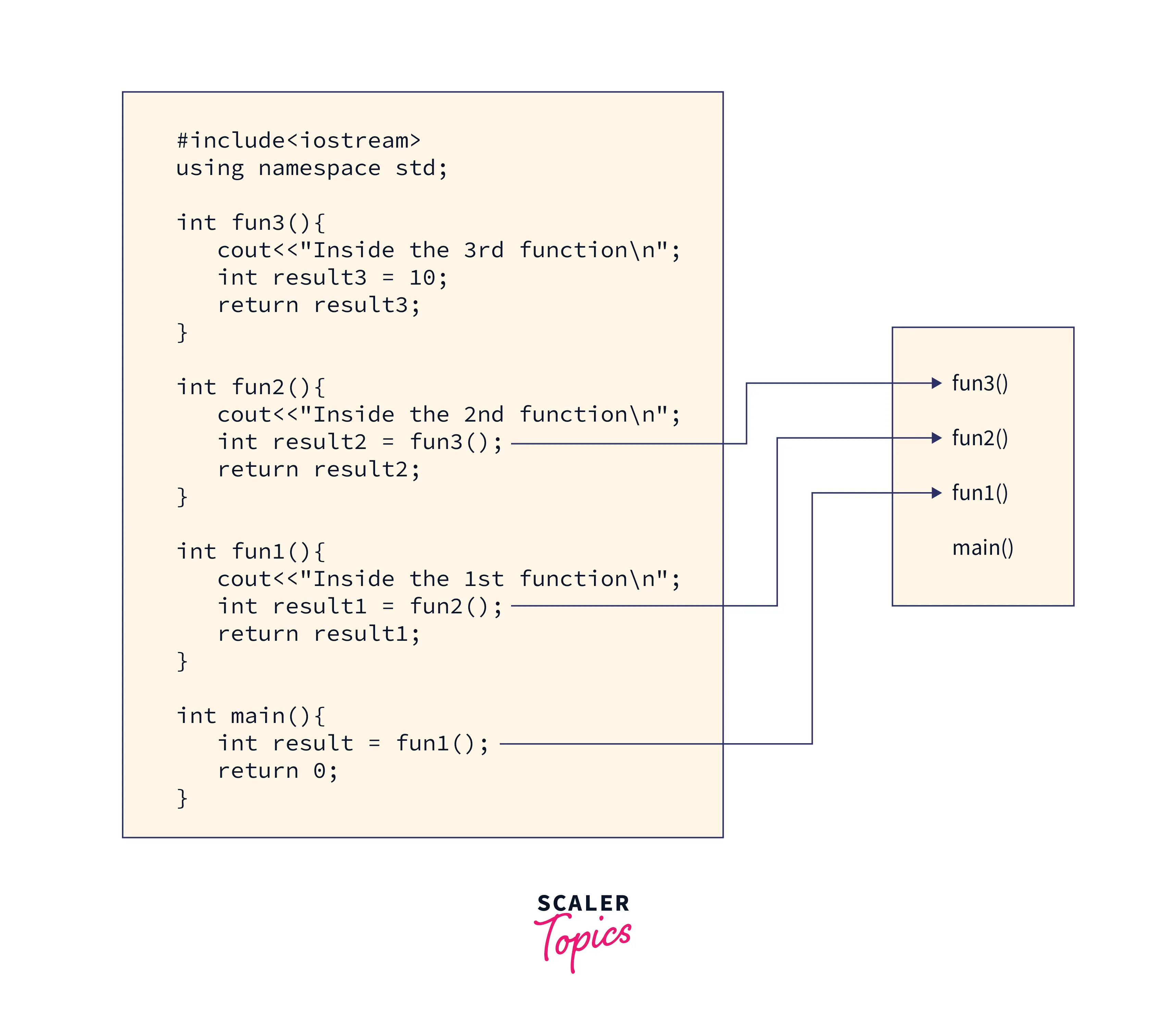
How to Solve a Particular Problem Using Recursion?

While solving a problem with recursion first thing we need to make sure is to search for a similar pattern in the different-different inputs of the same problem. If the solution for smaller input somehow contributes to the original solution, then recursion could be used to solve the problem.

As you can see, recursion generally consists of two components, namely a base condition and simple code with a recursive call.

• Look at the smallest possible valid input for the base condition.
• For the code, assume that the problem has already been solved for some smaller input, but it needs to be concatenated according to some manipulations in the current input and recursive call.
• Generalize the technique being explained in the above point.

Consider the example below to understand the concept.

Find the Factorial of a Number

1. Search for a similar pattern: The factorial exhibits a pattern which you can see in the image below.
2. Find Base Condition: The factorial exists only for whole numbers. Hence, 0 is the smallest valid input.
3. Now, as we have discussed the base condition and a similar pattern for the problem, it is time to think about a generalized pattern of the solution. See the next point for more description.
4. Suppose you've already calculated factorial(5) and now you have to calculate factorial(6). So, you just need to multiply 6 with the result of factorial(5). Notice that, here we are solving our big problem (factorial of 6) with the help of the result of a smaller problem (factorial of 5).
5. Generalization: Factorial of n = n * Factorial of (n-1)

Input:

Output:

Stack Overflow Error in Recursion

Recursion in C++ uses an internal stack to store information about the execution of the function. Each function call gets pushed onto the stack one after another, then the execution of the function definition begins. The function that is being executed is popped out of the stack when its base condition is met. This pop process is accompanied by providing the return value to the last immediate function call. So, when recursion takes too many steps/calls, the stack could fill up. In this case, the next immediate recursive call will be accompanied by a stack overflow error. It usually occurs either due to a lack of terminating condition in the recursive function, or sometimes it might be caused due to deep recursion technique, which means many calls have to be stored in the stack in order to reach the final solution.

Difference between Direct and Indirect Recursion

In the direct recursion technique, one function calls the same function from the function body.

While in the indirect recursion, the function can call a function X (let's say) and then this X can call another function Y and finally Y can call the original function.

Example: Print Natural Numbers

Again we have taken a simple example to print natural numbers. The recursive function will print numbers from 1 to given limit N.

1. Direct Recursion

Output:

Explanation:

• The directRecursion() recursive function is calling itself again and again hence it is direct recursion.

2. Indirect Recursion

Output:

Explanation:

• The indirectRecursion1() recursive function it is printing a number and then calls the indirectRecursion2() to print the next number, again the indirectRecursion2() is calling the indirectRecursion1() function. Hence, this is an example of indirect recursion.
• In the indirectRecursion function, one function is printing either odd or even numbers only, it depends on which function you have called first. In the main function we are calling the indirectRecursion1() first, so, it will always print odd numbers and indirectRecursion2() will print even numbers.

Difference between Tailed and Non-Tailed Recursion

Tailed Recursion

Recursive functions are referred to as tail recursive if they return some function call directly, meaning that the last statement in the body of the function is the recursive call. In this case, the compiler can perform some optimization while allocating the resources for the next recursive call. Here, compiler does not need to store the previous state of the last function call because that has finished execution. The function call can get executed in constant memory space so there is no possibility of a stack overflow error.

Example: Print Numbers till N

In this example, we are printing numbers up to N starting from a start point (default 1). This is a tail recursive function since the recursive call is the last statement of the function definition.

Output:

Explanation:

• Initially, we have defined a variable to store the start of the print, which is 1 in our case.
• In the recursive function, first of all, we are checking the base condition, i.e., stop recursion when the number is greater than N.
• After printing n at each call, we are calling the function with n+1 as a parameter. As the function call is the last statement of the function body, the example falls in the category of tailed recursion.

Non-Tailed Recursion

In the non-tailed recursion technique, the return is not the last statement in the function body. So here, compiler needs to store the previous state even after the return statement because there is something written in the function which might be dependent on the previous state.

Example: Summation of N Natural Numbers

In this example, we will find the sum of numbers from 1 to N. Although, it is quite simple to do with a straightforward loop, let's see how we can use a recursive function here. This is an example of non-tailed recursion in C++ because n + sumTillN(n-1) is being returned here instead of a recursive call.

Input:

Output:

Explanation:

• Initially, we have defined a variable to store the number to be passed in the recursive function.
• In the recursive function, first of all, we are checking the base condition, i.e., stop recursion when the number is equal to 1.
• A statement containing a recursive call is being returned from the function. The solution is the (sum from 1 to n-1) + n, which, in turn, provides the sum from 1 to n.

As we know tailed recursion is an efficient technique, let's see how we can turn a non-tailed recursion into a tailed one.

Conversion of Non-Tailed Recursion into Tailed Recursion

The basic idea to convert non-tailed recursion into tailed recursion is to pass an argument to store the result of each function call instead of keeping it on the stack.

Input:

Output:

Explanation:

• Initially, we have defined two variables to store the number to be passed in the recursive function and the one in which the sum will be stored.
• In the recursive function, first of all, we are checking the base condition, i.e., stop recursion when the number is equal to 0.
• Before returning the recursive call we are adding n in the currentSum variable.

Basic Overview of Iterative VS Recursive Code

Recursion and iteration are somewhat similar to each other. In recursion, there exists a call to the same function again and again to execute the function code. And in iteration, there exists a block of code that gets executed repeatedly. They both get terminated according to some specified condition.

It is easier to write recursive code since a lot of stuff is handled internally. It makes debugging difficult since the entire recursive tree, function call stack, and return values of recursive function calls need to be examined. Recursive functions do not usually follow a linear flow of code. On the other hand, loops are complex to write, but they're easier to debug because we can see the code that's running and the flow of code remains linear.

Recursion has overhead in terms of space and time complexity, including frame allocation in the stack for a function call, function call switching, memory allocation, and deallocation. Iteration does not have these overheads, making it better for this context.

Printing n^th Fibonacci Number

See this example to visualize the difference between the Iterative and Recursive code for the same problem statement.

Output:

Explantion:

• We have two functions to find n^th fibonacci number one is recursive and the other is iterative.
• In the recursive one, at each step, we are finding the Fibonacci number by calling the same function for $n-1$ and $n-2$ as a parameter and then summing them up.
• In the iterative one, at each step, we are finding the $nth$ fibonacci by the summation of ($n-1$)^th fibonacci and ($n-2$)^th fibonacci by reinitialising the value secondLast and last fibonacci numbers.
• Therefore, from the perspective of code execution, everything remains the same. You just need to figure out the logic of the problem. Both recursion and iteration can be used if the same code needs to be run multiple times. The choice is yours to determine how to express that logic through programming.

Advantages of Recursion

Less Code: One of the amazing advantages of using recursive functions is that we have to write less code to complete the complex tasks. Also, there exists several problem statements for which iterative code is much more difficult to write but recursion solves them within 8-10 lines.

Helpful in Non-Linear Data Structures: When there is a task to operate on non-linear data structure like tree, graph, etc. recursion provides an easy way to manipulate them.

No need to Implement Explicit Stack: If the function requires a stack to maintain some kind of order or something related information, the recursion could be the best choice because it provides us an inbuilt stack managed by the compiler. For example, postfix, and infix calculations become easy with recursion because we don't need to declare and manage an external stack.

Disadvantages of Recursion

Complicated Debugging: As recursion works in less code, everything happens underneath so it is difficult to analyze and resolve the bug in recursive code because it needs a recursive tree to be drawn to see the root cause of the bug.

Complexity Overhead: Recursive solutions are a little bit costlier in terms of space and time complexity because of the control switch between functions, information storage for several function call pushed into the stack, memory allocation and deallocation, etc.

Other Recursion Examples

After the entire discussion, it is time to explore some of the prominent examples of recursion.

Example 1: GCD of Two Numbers

In this example we are finding the greatest common divisor of two numbers by recursion. The euclidean algorithm is being used here.

Input:

Output:

Example 2: Power Function: xⁿ

Here our objective is to find xⁿ, let's see how recursion in C++ can help us.

Input:

Output:

Explanation:

• Initially, we had a variable and we passed it to a function which is recursively finding the power.
• The fact which is being utilized here as a common pattern is, $x$^$n$ = $x$ $*$ $x$^$n-1$.

See Also:

• Recursion in Java
• Euclidean Algorithm for GCD