Hyperparameters Tuning in Neural Networks

Introduction

Hyperparameter tuning is the process of finding the optimal values for the hyperparameters of a neural network. Hyperparameters affect the model's performance and are set before training. Hyperparameter tuning can improve a neural network's accuracy and efficiency and is essential for getting good results.

For example, the learning rate of a model can determine how fast the model learns. The model only fits the data well if the learning rate hyperparameter is too small or too big. Therefore, the right balance of Neural Network hyperparameters is important for the model's performance.

Several approaches to hyperparameter tuning include manual tuning, grid search, and random search.

What is Hyperparameter Tuning?

Hyperparameter tuning involves testing various combinations of hyperparameter values and returning the combination that produces the best performance.

What does it Do?

Hyperparameter tuning uses algorithms and tools and searches for the values of Epochs, Batch size, learning rate, etc. to find the best value combinations.

For example, suppose the range of epoch values to test is $50-500$. In that case, the hyperparameter tuning process will evaluate the model's performance with each value and return the optimal epoch value.

How does it Work?

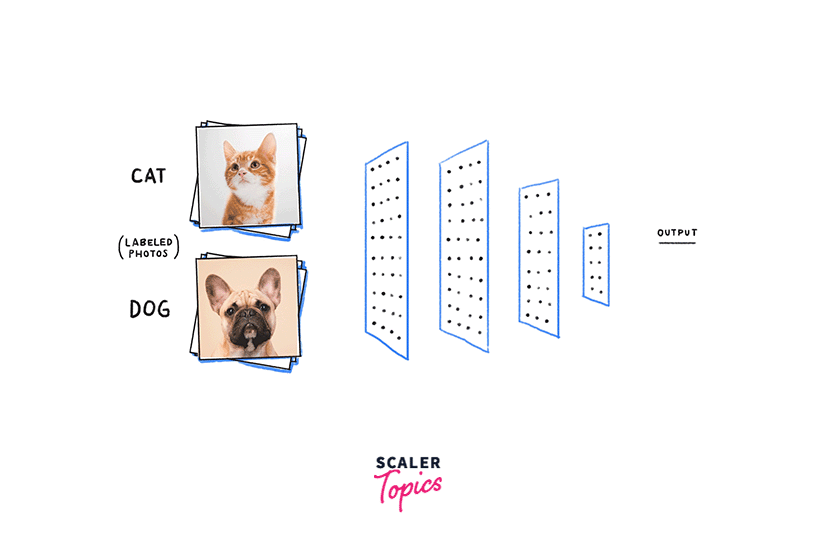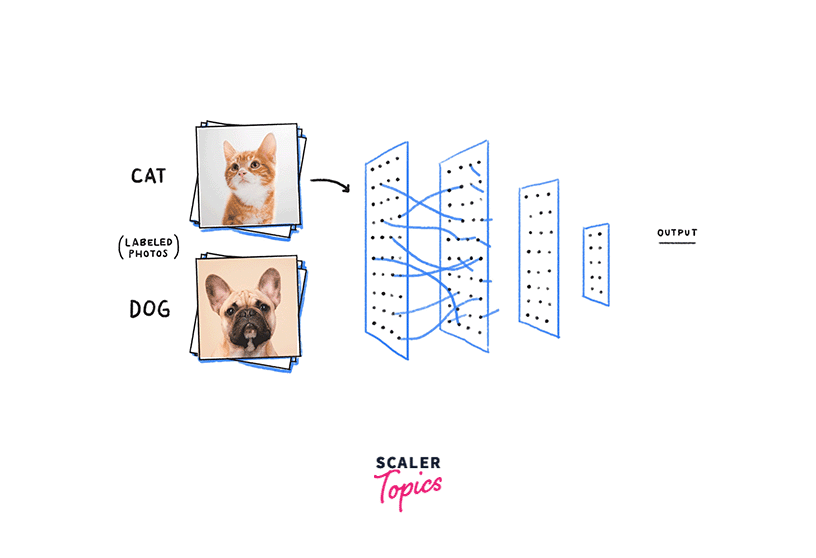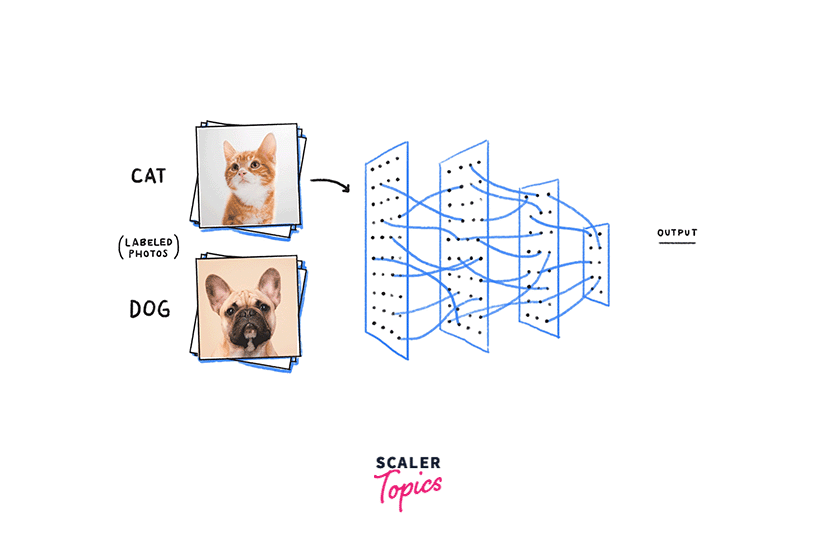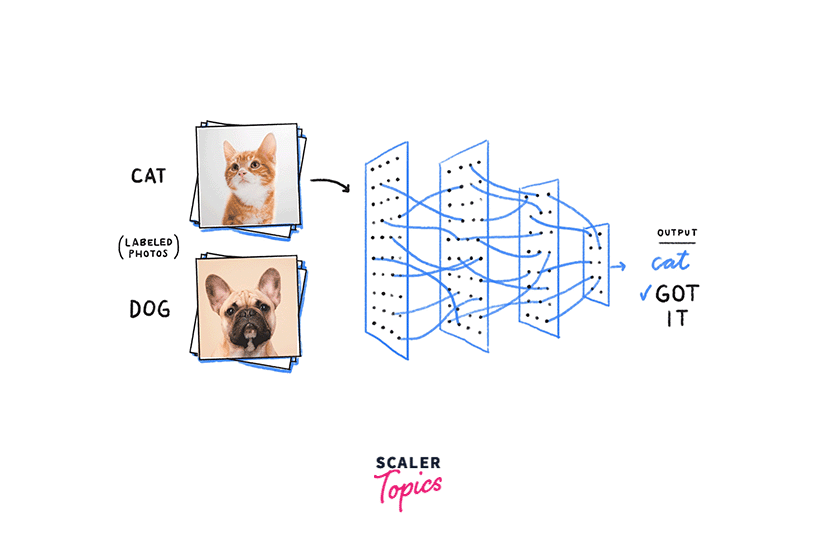
Let's say we are building a neural network to classify images of animals. Some Neural Network hyperparameters we want to tune include the learning rate, the number of layers in the network, and the batch size.

We can use grid search to find the optimal values for these hyperparameters. To do this, we first define a range of values for each hyperparameter we want to tune. For example, we might define the following ranges:

• Learning rate: 0.001 to 0.1.
• Number of layers: 1 to 5
• Batch size: 32 to 128

Next, we create a grid of all possible combinations of these values. For example, if we have the following values:

• Learning rate: 0.001, 0.01, 0.1
• Number of layers: 1, 3, 5
• Batch size: 32, 64, 128

Then the grid will have $27 (3 x 3 x 3)$ total combinations. We then train our neural network, evaluate a model for each combination, and record the results. For example, we might record the accuracy of each model on a validation set.

Finally, we chose the combination that produced the best results. Combining a learning rate of 0.01, 3 layers, and a batch size of 64 produced the highest accuracy. This combination would be the optimal values for the hyperparameters, and we would use these values to train the final model.

Tuning

Number of Hidden Layers

The number of hidden layers is a hyperparameter that can significantly impact the model's performance. Increasing the hidden layers can allow the model to learn more complex relationships in the data. Still, it can also increase the risk of overfitting and require more computational resources.

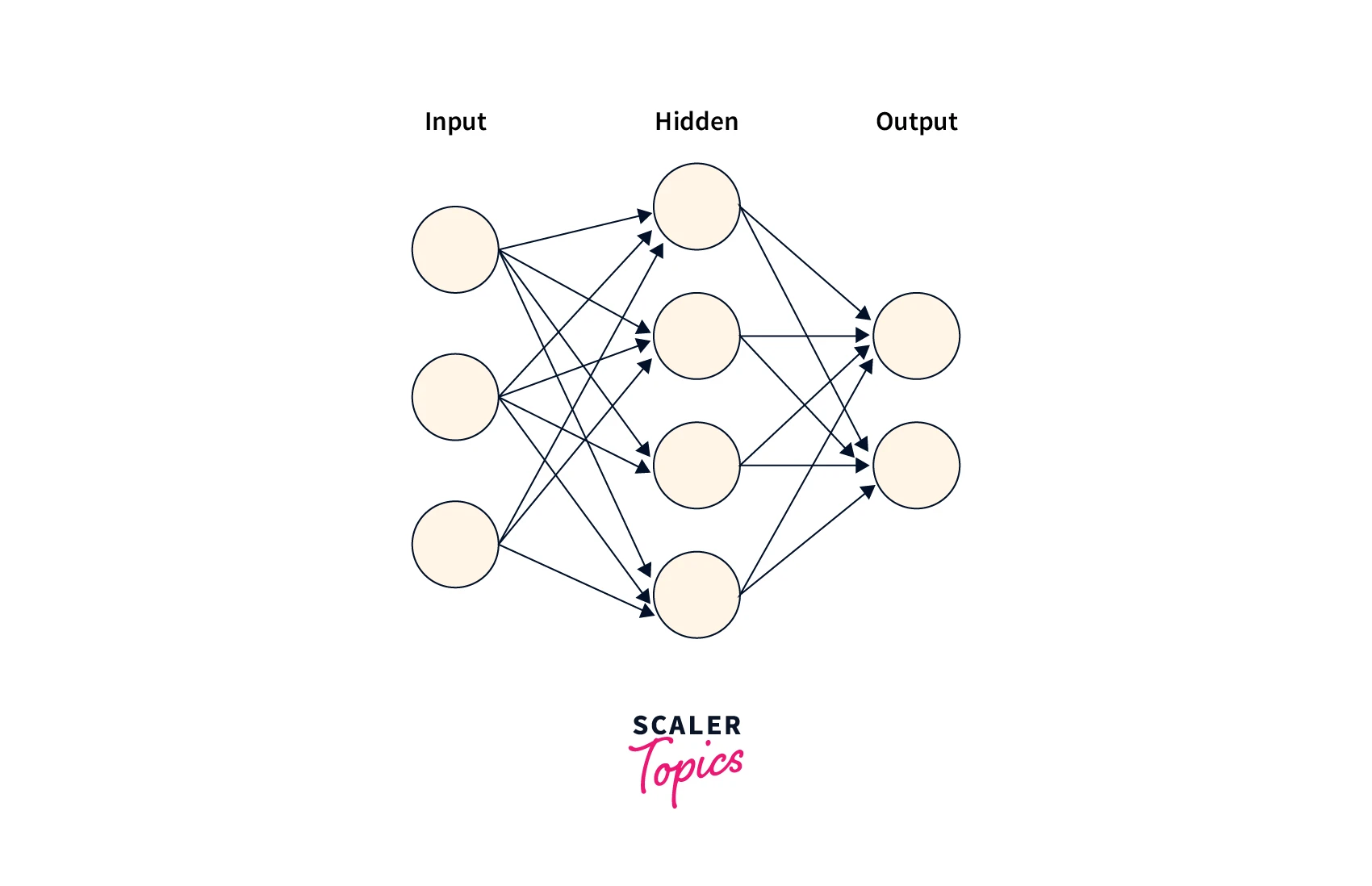
The optimal number of hidden layers can vary based on the problem's complexity and the dataset's size. Generally, a larger dataset and a more complex problem require a deeper network with more hidden layers. A smaller dataset and a simpler problem may require fewer hidden layers.

Number of Neurons Per Hidden Layer

The Number of Neurons per Hidden Layer behaves similarly to the number of layers. The number of Neurons increases with the complexity of the data. The number of Neurons in a Neural Network can vary with the chosen architecture. Increasing Neurons helps fit data better. While reducing layers can help reduce bias and faster training. Generally, the number of Neurons is increased until there is no improvement in performance. It is important to note that this parameter is also prone to overfitting.

Learning Rate

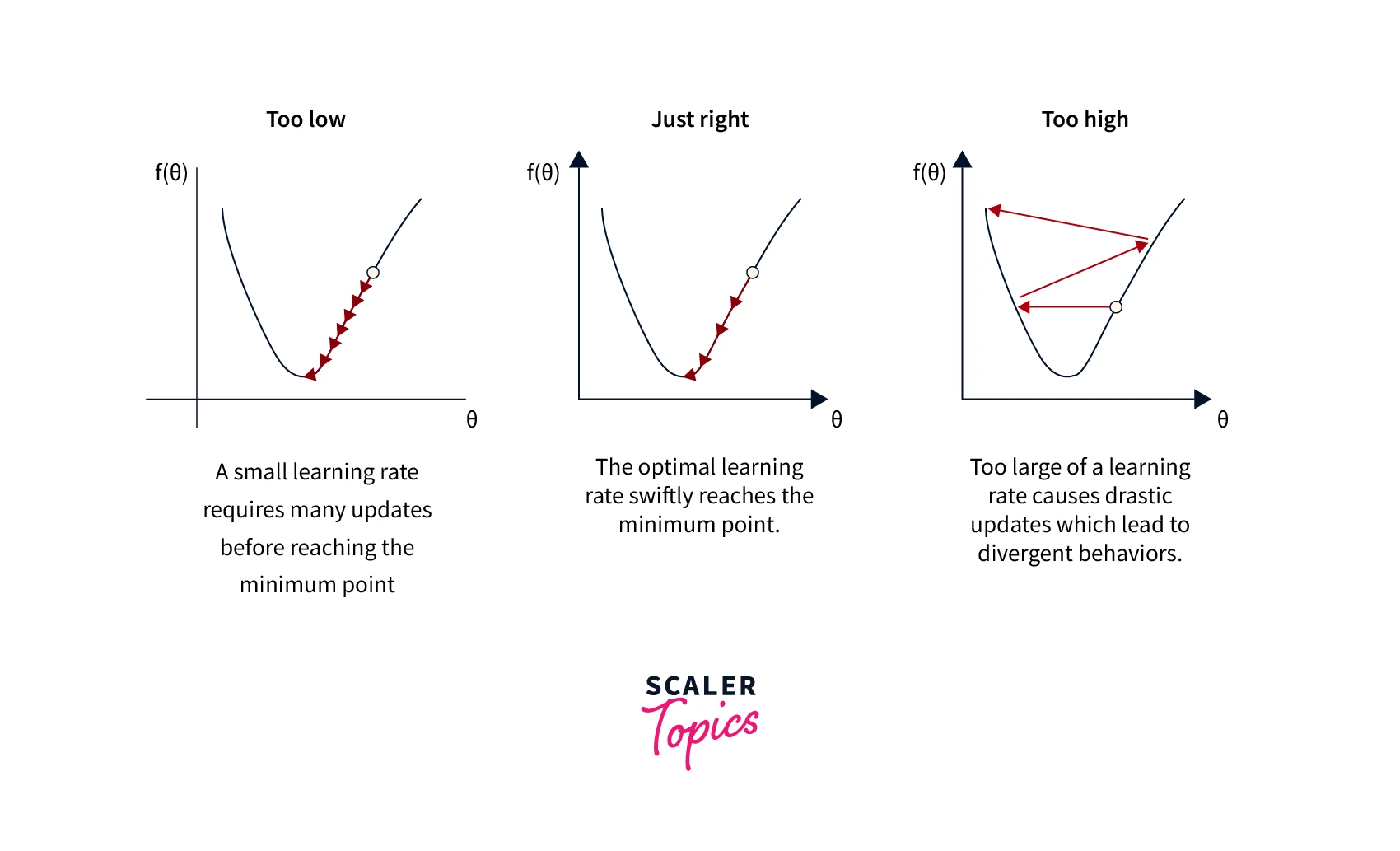
The learning rate is a hyperparameter in neural networks that determines the step size at which the optimizer updates the model weights during training. The learning rate can significantly impact the model's performance, as a lower learning rate may result in slower convergence but a more accurate model. In comparison, a larger learning rate may result in faster convergence but a less accurate model.

Batch Size

The batch size can impact the generalization performance of the model. A larger batch size may result in better generalization, allowing the model to average over more examples and reducing the model's weight variance. However, a very large batch size can also cause the model to to converge to a suboptimal solution, as it may result in a slower learning rate and a less noisy gradient.

A larger batch size may allow the model to perform more efficiently using the available hardware, as it can better use vectorized operations and parallelization. However, a large batch size can also cause memory issues, as it may require more memory to store the gradients and intermediate activations.

How to Avoid Overfitting while Tuning?

Overfitting is a common issue while training neural networks. It can be particularly problematic when hyperparameter tuning, as it can lead to selecting hyperparameters that work well on the training data but need to generalize better to unseen data.

Here are a few methods that can be used to avoid overfitting during Neural Network hyperparameter tuning:

• Use a separate validation set to evaluate the model's performance during hyperparameter tuning.
• Using regularization techniques, such as weight decay (L2 regularization) or dropout, prevents the model from overfitting to the training data.
• Implement early stopping from terminating the training process if the model's performance on the validation set starts to degrade.
• During training, the model's performance is monitored on a separate validation set, and the training process is terminated when the model's performance on the validation set starts to degrade. This is based on the assumption that the model's performance on the validation set will generally improve as the training progresses until it reaches a certain point where the model starts to overfit the training data. By interrupting the training process at this point, early stopping can help prevent the model from overfitting the training data.

Functions for Hyperparameter Tuning

Several approaches can be used to perform hyperparameter tuning on neural networks, including grid search, random search, and Bayesian optimization.

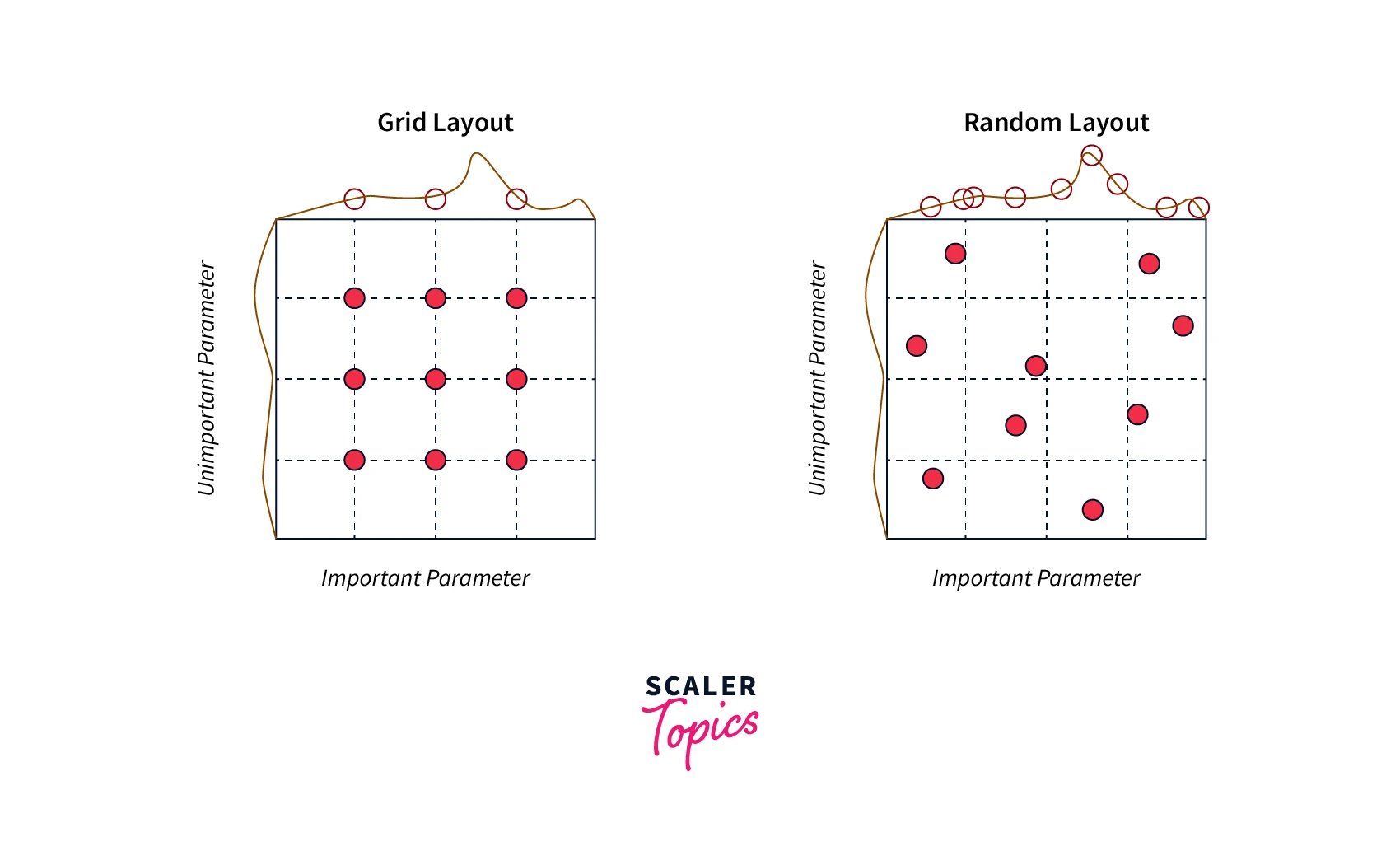
Grid Search

Grid search is a hyperparameter tuning method involving specifying a grid of hyperparameter values and training and evaluating the neural network model for each combination of hyperparameter values. For example, if we want to tune the learning rate and the batch size of a neural network, we can specify a grid of possible values for the learning rate (e.g., 0.1, 0.01, 0.001) and the batch size (e.g., 32, 64, 128) and train and evaluate the model for each combination of values. The combination of hyperparameters that results in the best results on the validation set is then selected as the optimal set of hyperparameters.

Random Search

Random search is another hyperparameter tuning method involving sampling random combinations of hyperparameter values and training and evaluating the neural network model for each combination. Random search can be more efficient than grid search, as it does not require the evaluation of all possible combinations of hyperparameters.

Random Search can be better than grid search, especially if the most optimal values for the model are in between the specified values. For example, if the most optimal learning rate is 0.05 and the specified values are 0.01 and 0.1, then the grid search will not give good results, while the random search can get the optimal value.

Bayesian Optimization

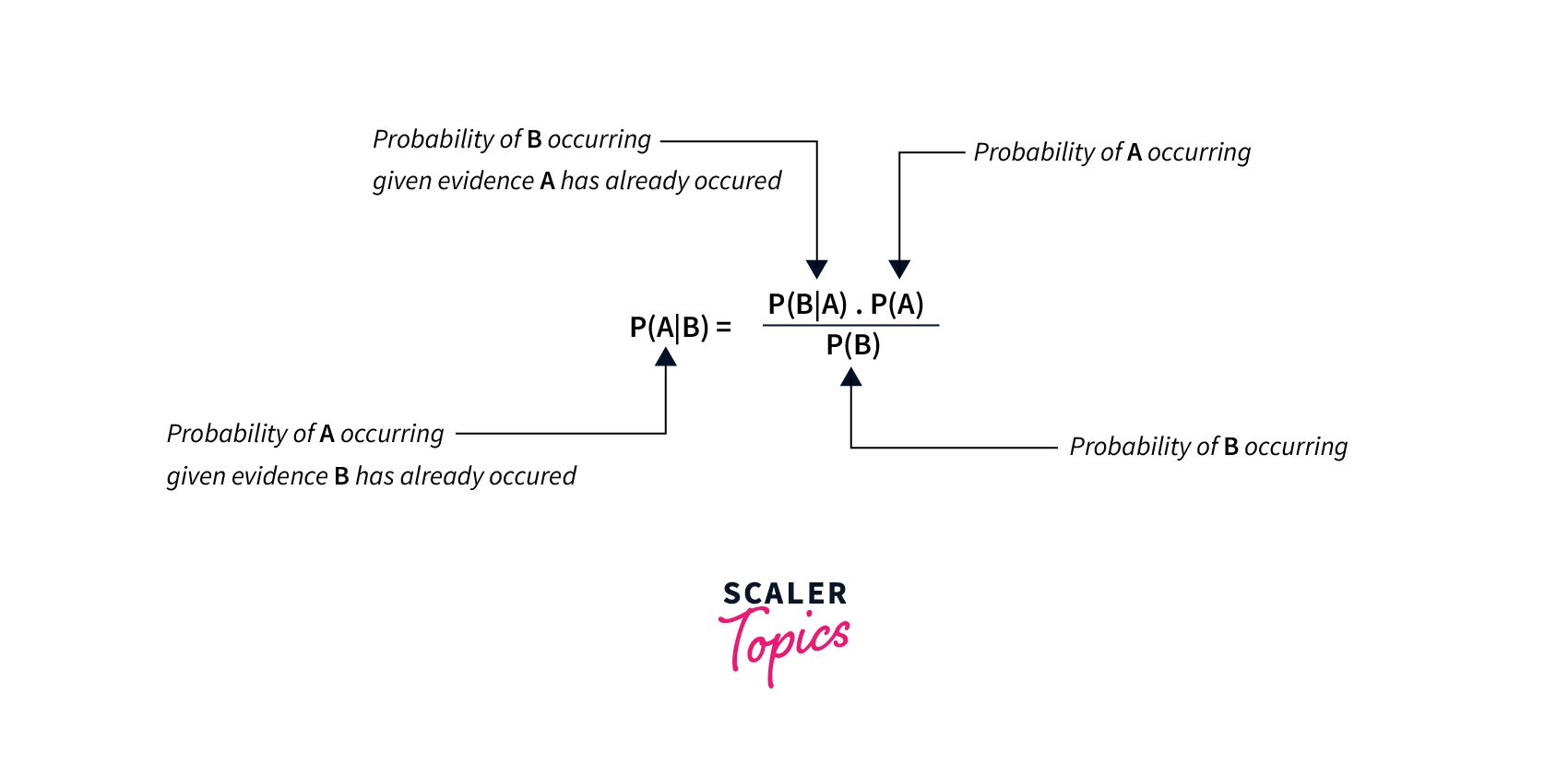
Bayesian optimization is a more advanced method of hyperparameter tuning that uses a probability function based on the hyperparameters and accuracy score to model the distribution of the hyperparameters and their impact on the model's performance.

Bayesian optimization uses the previous values of scores and probabilities to make an informed decision in the following iterations. Allowing the model to focus on the hyperparameters that can significantly change the results while not focusing on the parameters doesn't affect the result much.

Bayesian optimization can be more efficient than grid search or random search, as it can adaptively select the next set of hyperparameters to evaluate based on the previous evaluations. However, it can be more computationally expensive and require more resources.