PyTorch Geometric

What is PyG (PyTorch Geometric)?

PyTorch Geometric (PyG) is a python library for deep learning on irregular structures, such as graphs, point clouds, and manifolds. It is built upon the popular PyTorch framework and provides optimized throughput of GPU-accelerated computation on sparse and irregular data of variable sizes.

The PyG library consists of various methods for geometric deep learning from published papers which can be used to perform tasks like node classification, graph classification, or link prediction. In addition, it contains mini-batch loaders for operating on many small or single giant graphs, multi GPU-support, DataPipe support, distributed graph learning via Quiver, and helpful transforms both for arbitrary graphs as well as 3D meshes or point clouds.

It is an intuitive and powerful framework that enables researchers to easily implement graph neural networks for a wide range of applications related to structured data.

Reasons to Try Out PyTorch Geometric on Graph-structured Data?

• Optimized throughput for highly sparse and irregular data:
  PyTorch Geometric provides dedicated CUDA kernels for sparse data and mini-batch handlers for varying sizes, allowing users to make the most of their GPU resources when dealing with graph-structured data.
• Support for both CPU and GPU computing:
  PyTorch Geometric is capable of running on both CPU and GPU, making it accessible to a wide variety of users regardless of hardware constraints.
• Easy-to-use tools:
  PyTorch Geometric contains easy-to-use mini-batch loaders as well as helpful transforms which enable researchers to quickly implement learning tasks related to graph structures with minimal effort.
• Comprehensive library of methods:
  The library consists of various methods for geometric deep learning from published papers, allowing users to easily apply the latest research on their data.
• Flexible library:
  PyTorch Geometric is a flexible library that can be used for tasks such as node classification, graph classification, or link prediction.

Requirements & Installation

There are a few requirements before proceeding with the installation. They are:

• Python 3.6 or higher.
• PyTorch 1.5 or higher (1.7 is recommended).
• CUDA 10+ (for GPU support).

Installation

Step - 1: Install PyTorch by running (CPU version)

Creating and Training a GNN Model

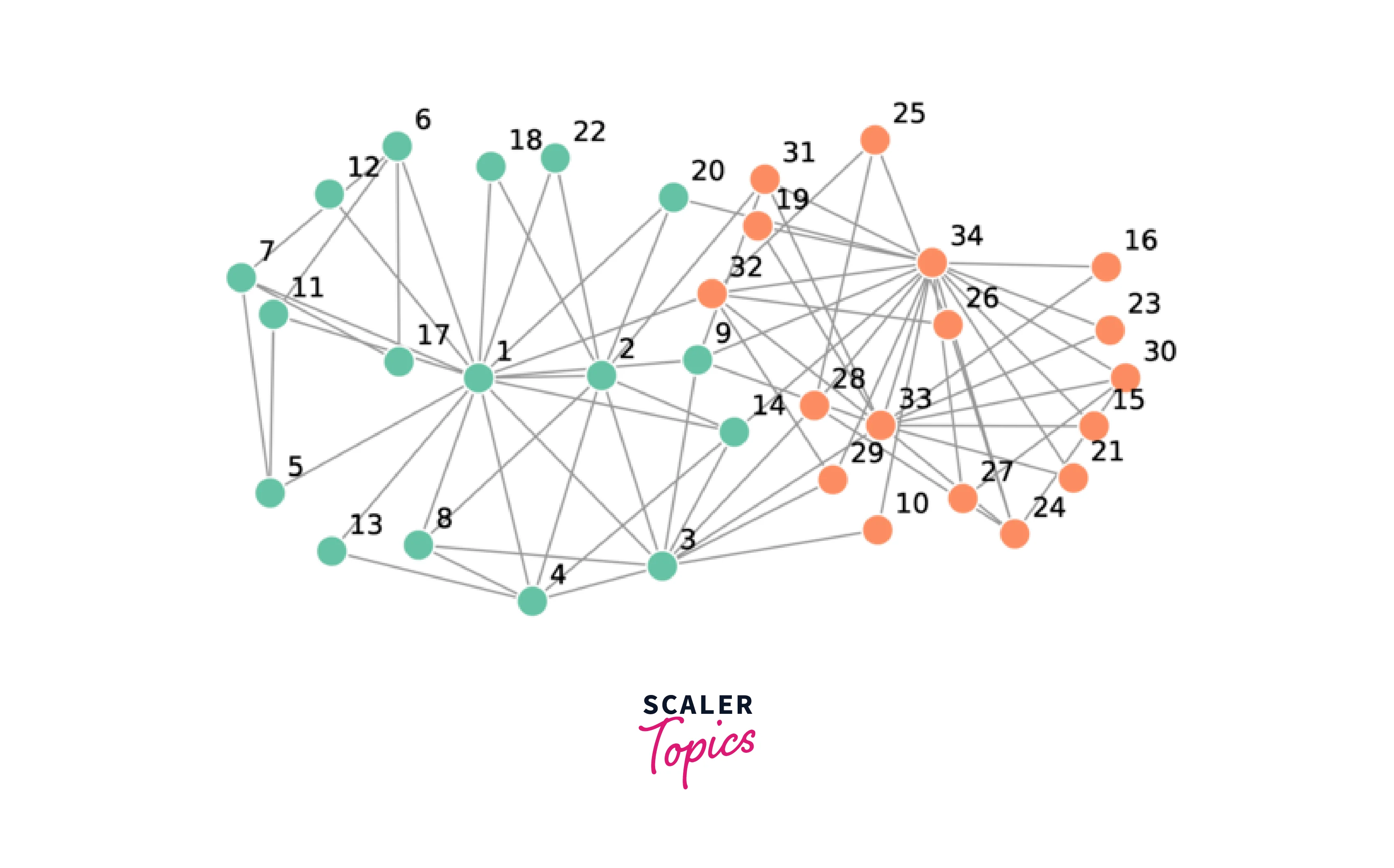
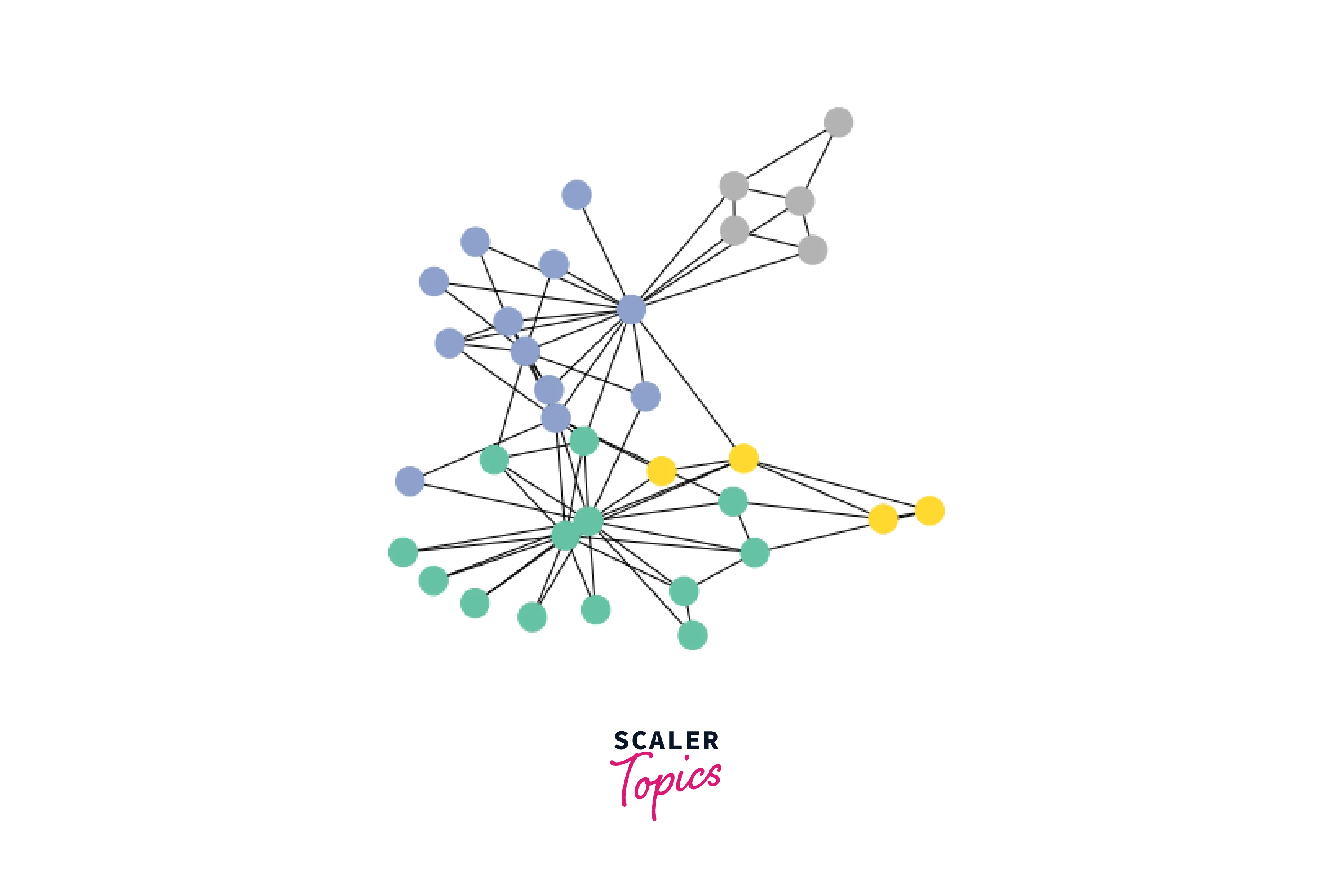
We can use a graph dataset, such as Zachary's Karate Club, for a node classification task. The dataset has 34 nodes representing club members and 78 links representing interactions between them. The nodes are labeled as belonging to one of two factions. We can use the train set to build a graph neural network model, and then use this model to predict the faction of nodes in the test set.

The standard 78 edge network data set for Zachary's karate club is publicly available on the internet. The data can be summarized as a list of integer pairs. Each integer represents one karate club member and a pair indicates the two members interacted. The data set is summarized below.

A simple visualization of Zachary’s Karate Club graph dataset looks like this:

First, we import the necessary modules from PyG such as a torch, GCNConv, and KarateClub dataset.

PyTorch Geometric provides easy access to this dataset via the torch_geometric.datasets subpackage:

After initializing the KarateClub dataset, we first can inspect some of its properties. For example, we can see that this dataset holds exactly one graph and that each node in this dataset is assigned a 34-dimensional feature vector (which uniquely describes the members of the karate club). Furthermore, the graph holds exactly 4 classes, which represent the community each node belongs to.

Gathering Information about the Graph

Let's now look at the underlying graph in more detail:

Each graph in PyTorch Geometric is represented by a single Data object, which holds all the information to describe its graph representation. We can print the data object anytime via print(data) to receive a summary of its attributes and their shapes:

We can see that this data object holds 4 attributes:

1. The edge_index property holds the information about the graph connectivity, i.e., a tuple of source and destination node indices for each edge. PyG further refers to
2. node features as x (each of the 34 nodes is assigned a 34-dim feature vector), and to
3. node labels as y (each node is assigned to exactly one class).
4. There also exists an additional attribute called train_mask, which describes for which nodes we already know their community assignments. In total, we are only aware of the ground-truth labels of 4 nodes (one for each community), and the task is to infer the community assignment for the remaining nodes.

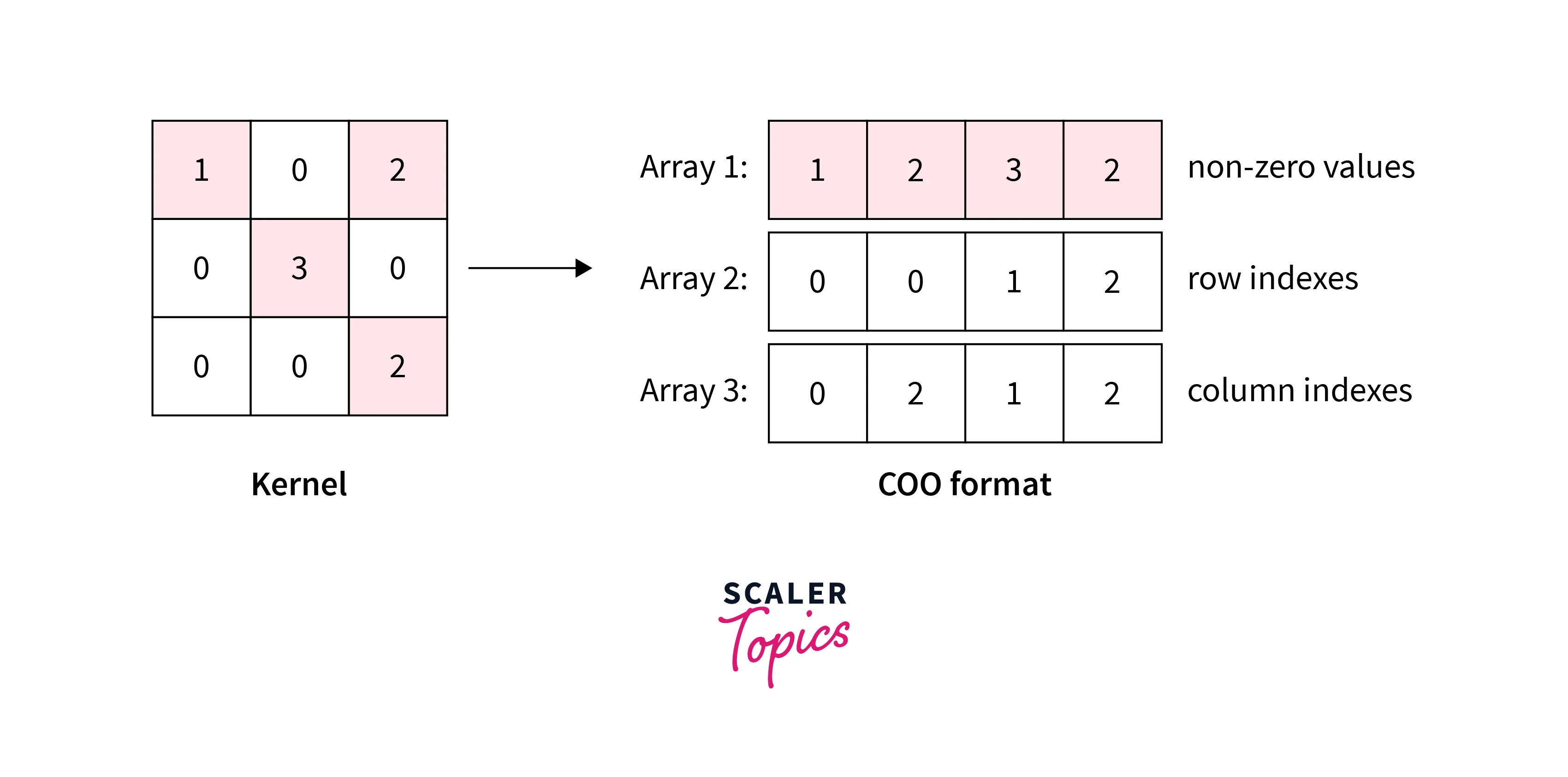
Let us now inspect the edge_index property in more detail:

By printing edge_index, we can understand how PyG represents graph connectivity internally. We can see that for each edge, edge_index holds a tuple of two node indices, where the first value describes the node index of the source node and the second value describes the node index of the destination node of an edge.

This representation is known as the COO format (coordinate format) commonly used for representing sparse matrices.

Visualizing the Graph Using NetworkX

We can further visualize the graph by converting it to the network library format, which implements, in addition to graph manipulation functionalities, powerful tools for visualization:

Implementing Graph Neural Networks

After learning about PyG's data handling, it's time to implement our first Graph Neural Network. PyG implements this layer via GCNConv, which can be executed by passing in the node feature representation x and the COO graph connectivity representation edge_index.

With this, we are ready to create our first Graph Neural Network by defining our network architecture in a torch.nn.Module class:

Here, we first initialize all of our building blocks in __init__ and define the computation flow of our network in forward.

We first define and stack three graph convolution layers, which correspond to aggregating 3-hop neighborhood information around each node (all nodes up to 3 "hops" away).

In addition, the GCNConv layers reduce the node feature dimensionality to $2$, i.e., $34 \rightarrow 4 \rightarrow 4 \rightarrow 2$. Each GCNConv layer is enhanced by a tanh non-linearity.

After that, we apply a single linear transformation torch.nn.Linear that acts as a classifier to map our nodes to 1 out of the 4 classes/communities.

We return both the output of the final classifier as well as the final node embeddings produced by our GNN.

We proceed to initialize our final model via GCN(), and printing our model produces a summary of all its used sub-modules.

Embedding Visualization

Let's take a look at the node embeddings produced by our GNN. Here, we pass in the initial node features x and the graph connectivity information edge_index to the model, and visualize its 2-dimensional embedding.

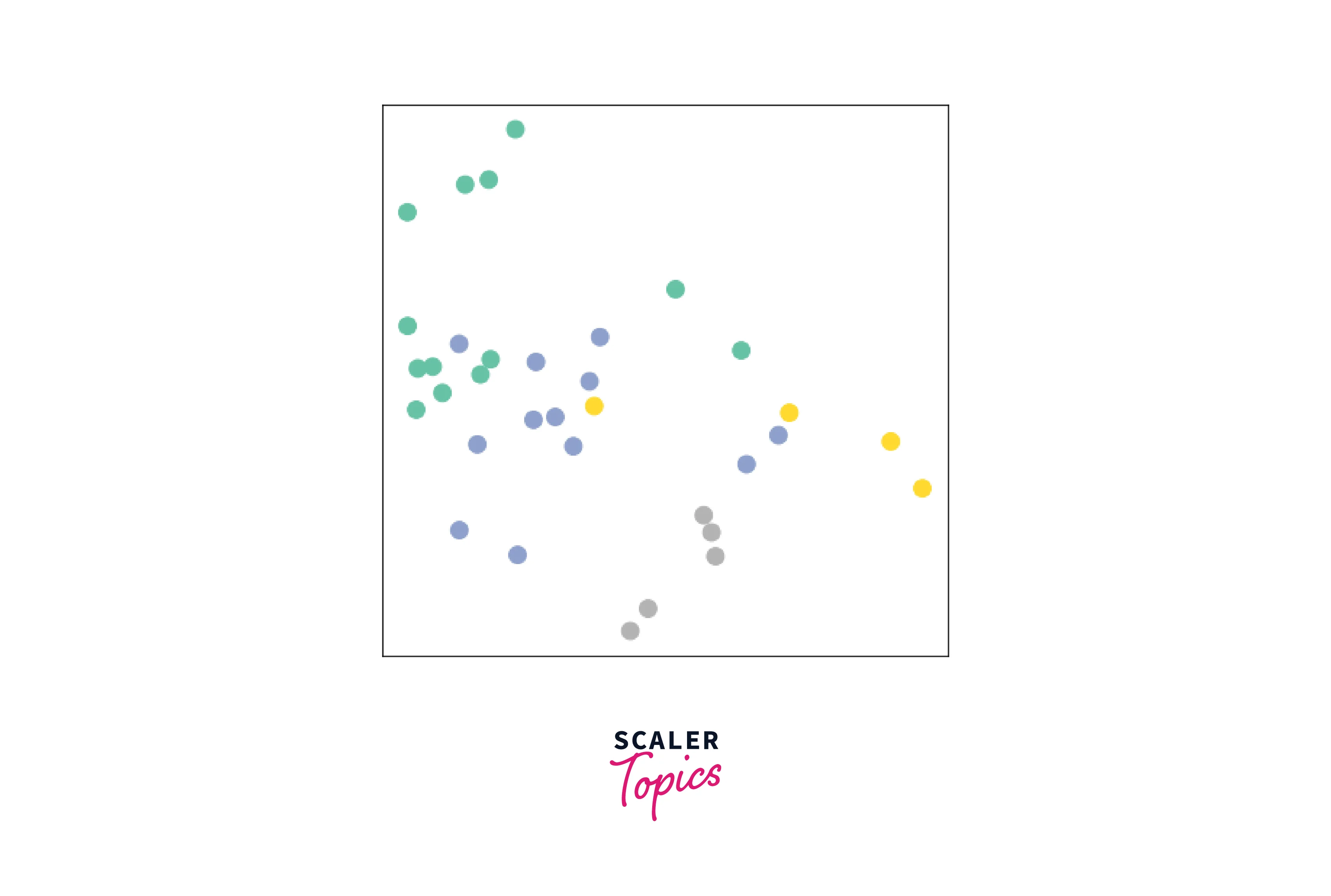
Remarkably, even before training the weights of our model, the model produces an embedding of nodes that closely resembles the community structure of the graph. Nodes of the same color (community) are already closely clustered together in the embedding space, although the weights of our model are initialized completely at random and we have not yet performed any training so far! This leads to the conclusion that GNNs introduce a strong inductive bias, leading to similar embeddings for nodes that are close to each other in the input graph.

Training on the Karate Club Network

Training our model is very similar to any other PyTorch model.

In addition to defining our network architecture, we define a loss criterion (here, CrossEntropyLoss) and initialize a stochastic gradient optimizer (here, Adam).

After that, we perform multiple rounds of optimization, where each round consists of a forward and backward pass to compute the gradients of our model parameters w.r.t. to the loss derived from the forward pass.

As one can see, our 3-layer GCN model manages to linearly separate the communities and classify most of the nodes correctly.

Furthermore, we did this all with a few lines of code, thanks to the PyTorch Geometric library which helped us out with data handling and GNN implementations.

Looking to excel in the field of AI? Our Deep Learning Free Course is designed to guide you toward becoming proficient in neural networks. Enroll today!