Python Program to Find Factorial of a Number

What is Factorial?

The factorial is the product of all the numbers less than or equal to the given number till 1. For example, the factorial of $7$ will be $7*6*5*4*3*2*1$, which is $5040$.

The factorial of a number is denoted by an exclamation sign $(!)$ in Mathematics. For example, the factorial of 7 is denoted as $7!$, similarly the factorial of any number N is denoted as $N!$

For any number N greater than 0, we can write:

$N! = N * (N-1) * (N-2) * (N-3) * … * 3 * 2 * 1$

Factorial of a Number using For Loop

In the following set of programs, we will see how to calculate the factorial of a number using the help of a for-loop in Python. We will run the loop from 1 to the given number. At each step, the value of the loop control variable (i.e., i) gets multiplied by the variable fact, which stores the value of the factorial of the given number.

For non-negative numbers

Code:

Input:

Output:

Explanation -

The loop runs from 1 to num i.e. 7, and every time ‘i’ gets multiplied to the variable ‘fact’. So, corresponding values of ‘i’ and ‘fact’ at each iteration are

Factorial of a Number using If Else with For Loop(For negative integers as well)

In the following programs, we will add an if-else statement to handle the cases where the value of the given number is negative. Apart from that, the logic for calculating the factorial will be the same as used above in the case of for-loop.

Code:

Input:

Output:

2. Input:

Output:

Explanation:

The control goes to the elif statement, and 1 gets printed which is the value of 0!.

Input:

Output:

Factorial of a Number using Recursion

In the following program, we will use recursion to find the factorial of a number. We can use recursion by simplifying the problem into smaller sub-problems. The factorial of a number N is represented as N! and can be calculated as N multiplied by the factorial of N-1. The base case is when N is equal to 0, in which case the factorial is 1. Recursion continues until reaching the base case, and then the final factorial of N is calculated using the results from each step. In summary, for N < 0, the factorial does not exist; for N = 0, factorial(0) is 1; and for N > 0, factorial(N) is N multiplied by factorial(N-1).

Code:

Output:

Explanation:

Here we want to find the factorial of 4, and we see the function named ‘fact’ recursively calls itself until we reach 0. And since we already know the factorial of 0. We will use this value to calculate the factorial of 1, 2, and so on up to 4.

We can understand the working better with the diagram given below:

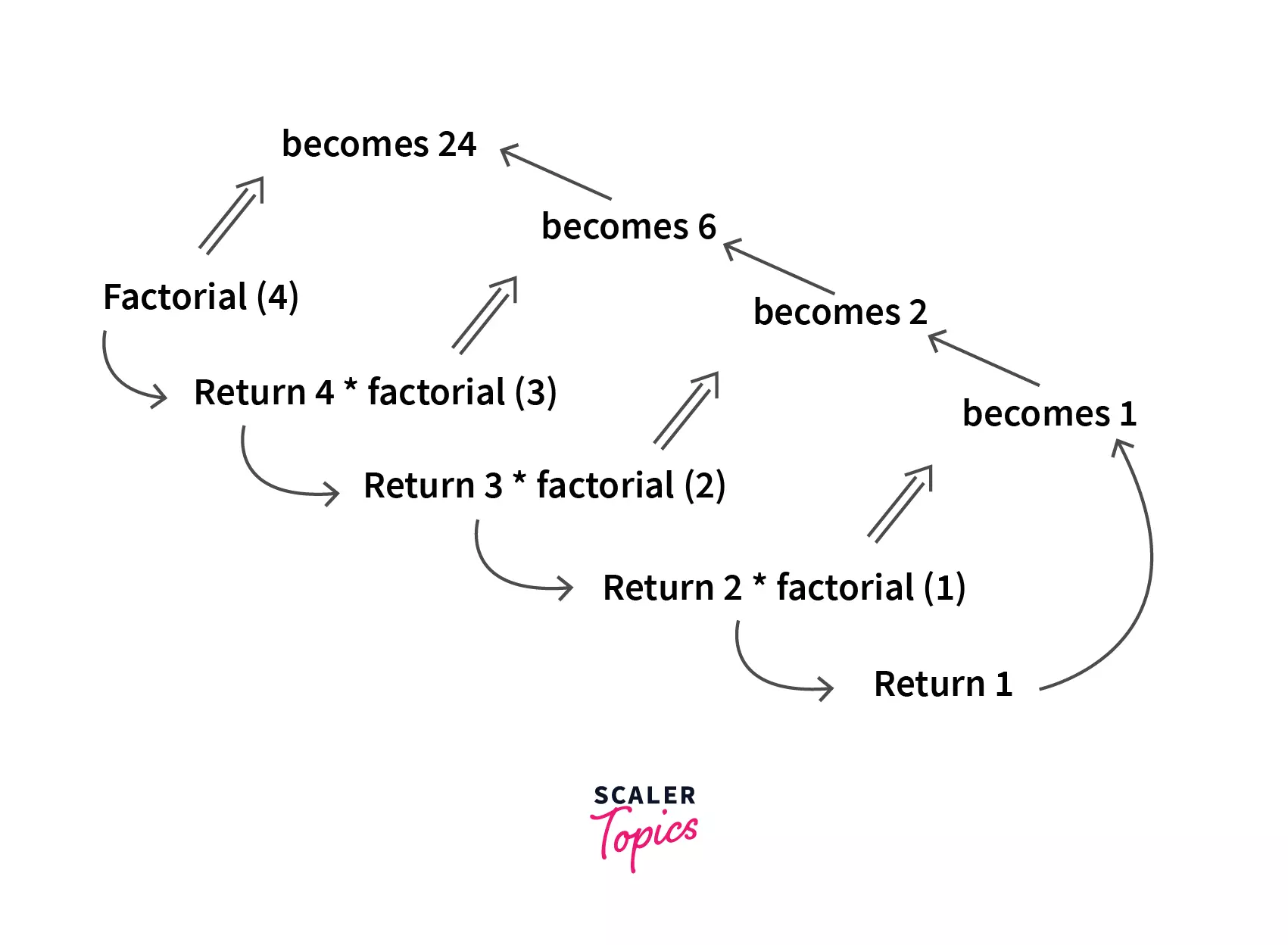
Rest for zero and -5 control goes to elif and else cases respectively.

Read more on Factorial of a number using recursion to understand it in more detail.

Using Math Module in Python Factorial Program

In the following program, we will be using the factorial() function, which is present in the Math module in Python to calculate the factorial of a given number.

This function accepts only a positive integer value, not a negative one. Also, this method accepts integer values not working with float values. If the value is negative, float, string, or any data type other than an integer, it throws a ValueError.

Output:

Using Ternary Operator in Python Factorial Program

In the following programs, we will use the same recursive code that we have seen above, the difference being that instead of the if-else conditional statement, we will use the ternary operator, which is also a type of conditional statement.

In a ternary statement, the format is like:

[on_true] if [expression] else [on_false]

Code:

Output: