Find MEX of Each Subtree

Problem Statement

Given a generic tree, where every tree node's value is in the range [0, N-1] where N is the number of nodes in the given tree, and the root node of the tree always has data as 0. For every node, the value/weight is given in the corresponding array named value. Find the MEX of every node from the given tree. (Basically: Find Mex in a tree)

A generic tree is a tree data structure where every node of the tree may have zero or more children. The Generic trees are the N-ary trees.

The Minimum excludant or MEX value of node V is defined as the smallest missing positive number in a tree rooted at node V.

Example

Example 1

For a better understanding of the problem statement, let's consider the below tree with its corresponding node values/weights. For the given tree we need to find the MEX of every node and store them in the array and return the array which contains values of MEX for every node in the given tree:

Input:

The tree formed from the given nodes is shown in the below image

value_arr : [3, 0, 1, 2, 6, 7, 4, 5]

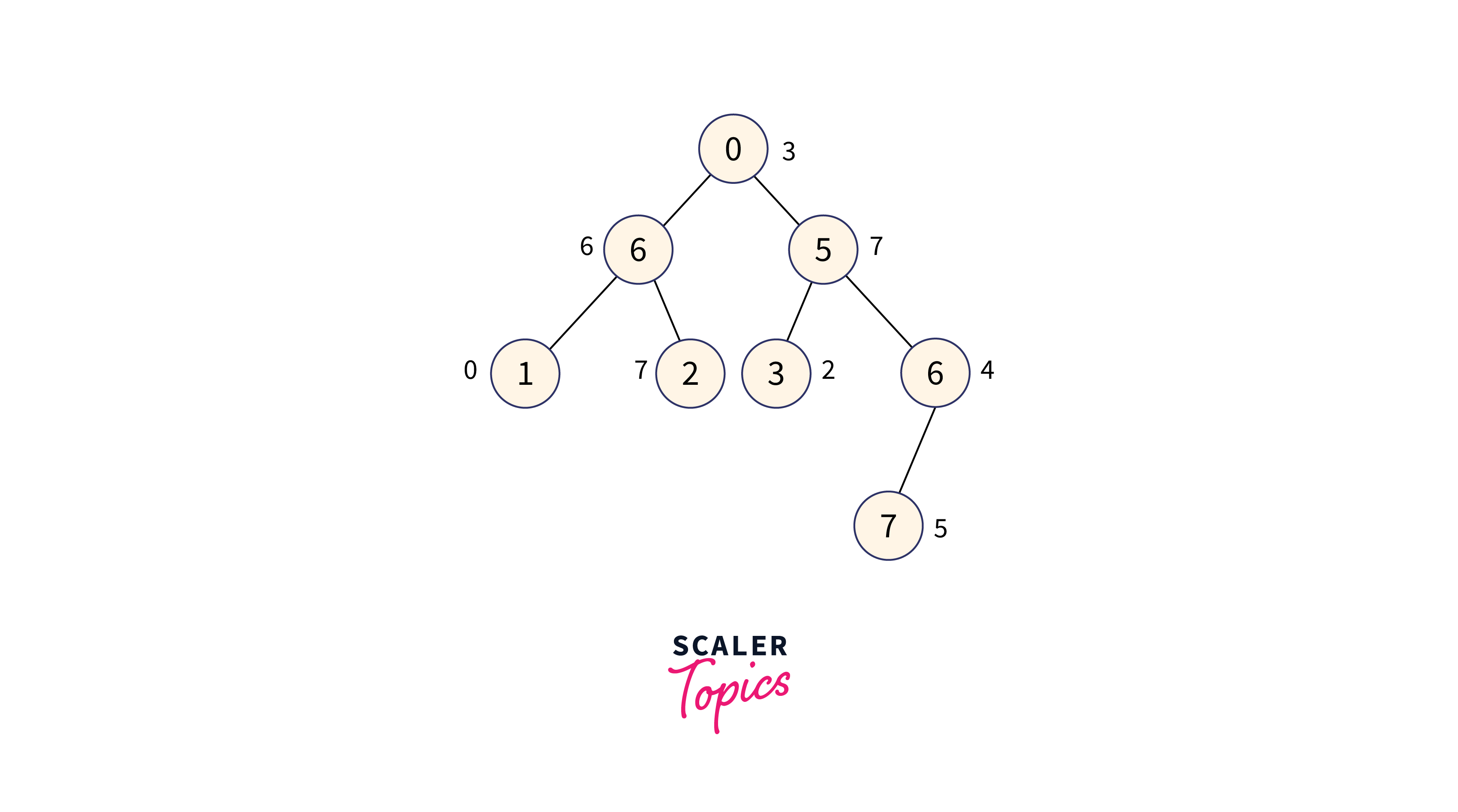
Output

[8, 1, 0, 0, 2, 0, 0, 0]

Explanation:

For every node in the given tree in the range [0, 7] where 8 represents the number of nodes in the tree, the MEX obtained is as follows:

• For node 0:

  Subtree with node 0 as the root node is formed as shown in the below image:

  

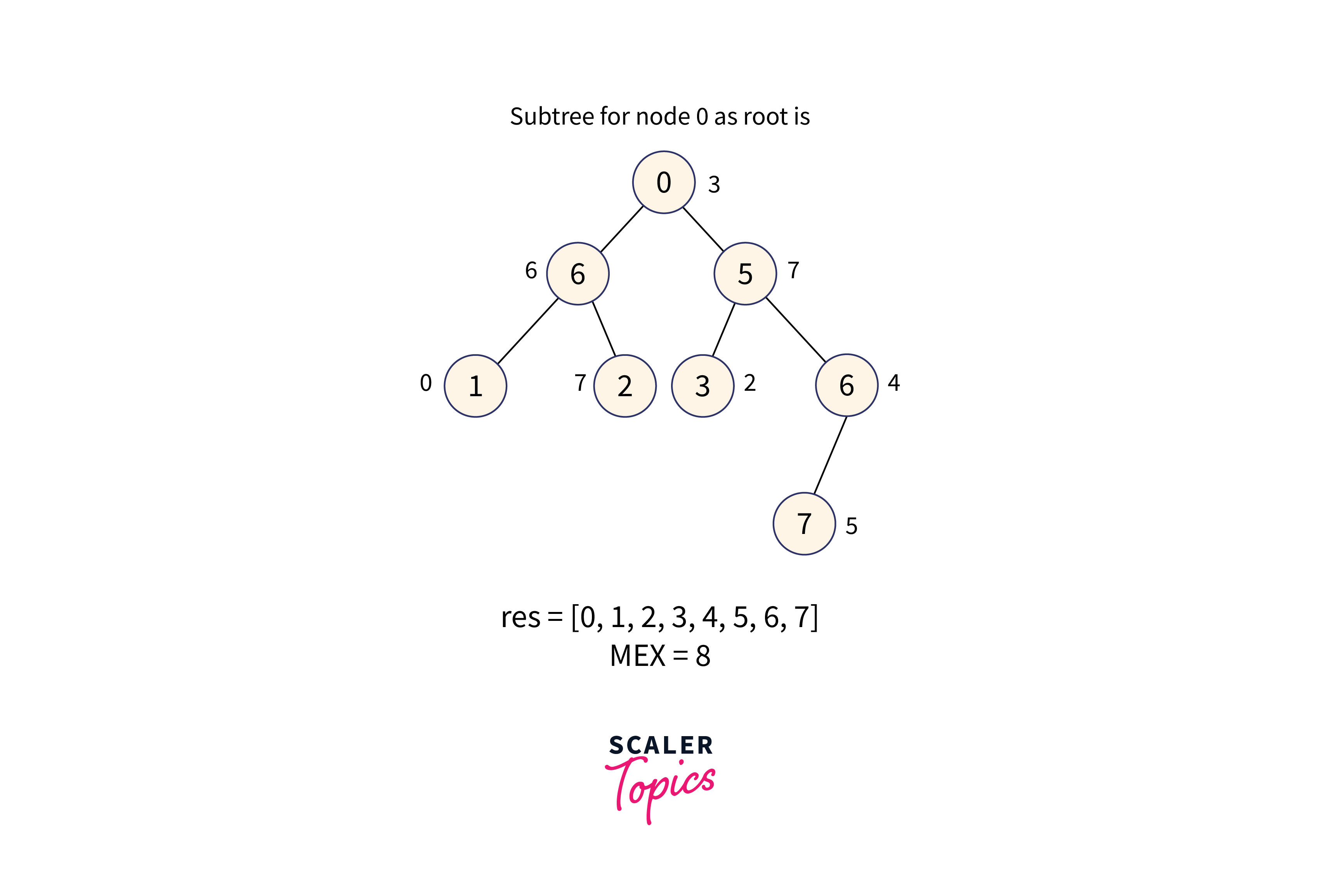
  The subtree of node 0 contains all values in the range [0, 7] therefore the minimum missing number is 8.

• For node 1:

  Subtree with node 1 as the root node is formed as shown in the below image:

  

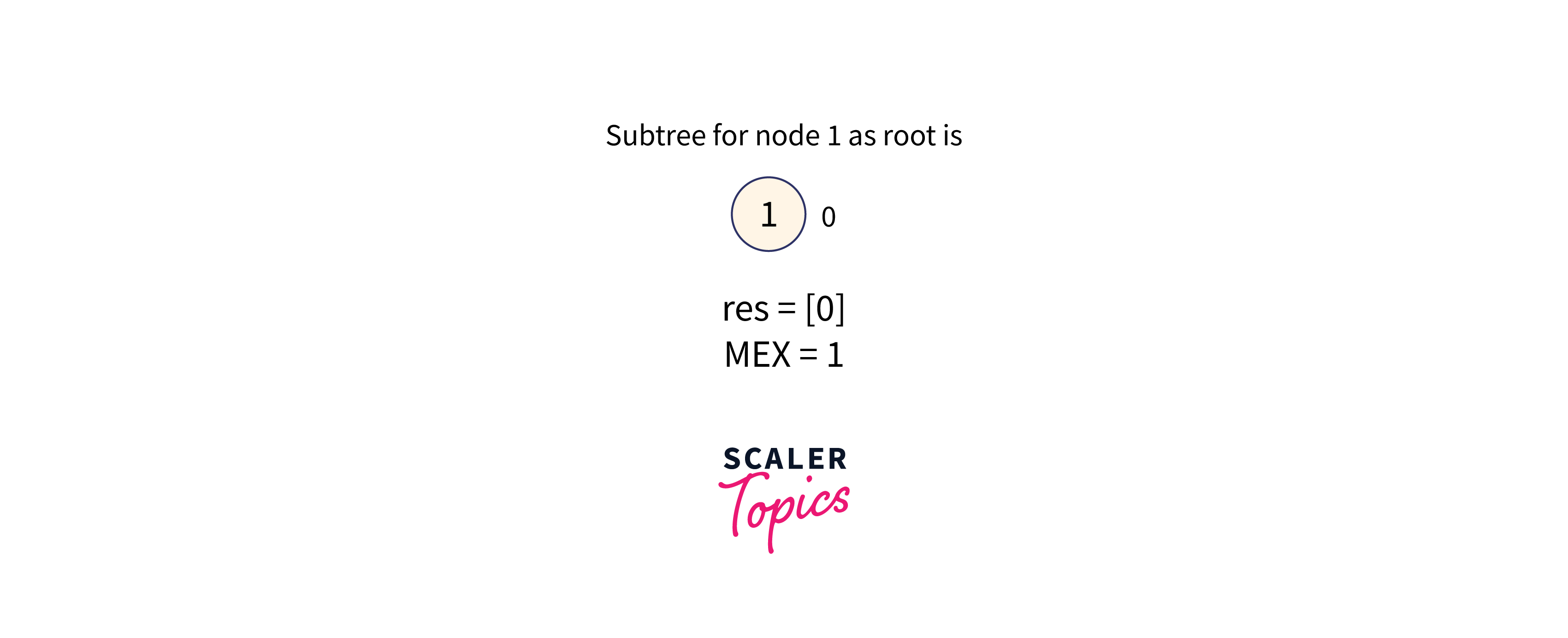
  The subtree of node 1 contains the value: [0], therefore the minimum missing number in the range is 1.

• For node 2:

  Subtree with node 2 as the root node is formed as shown in the below image:

  

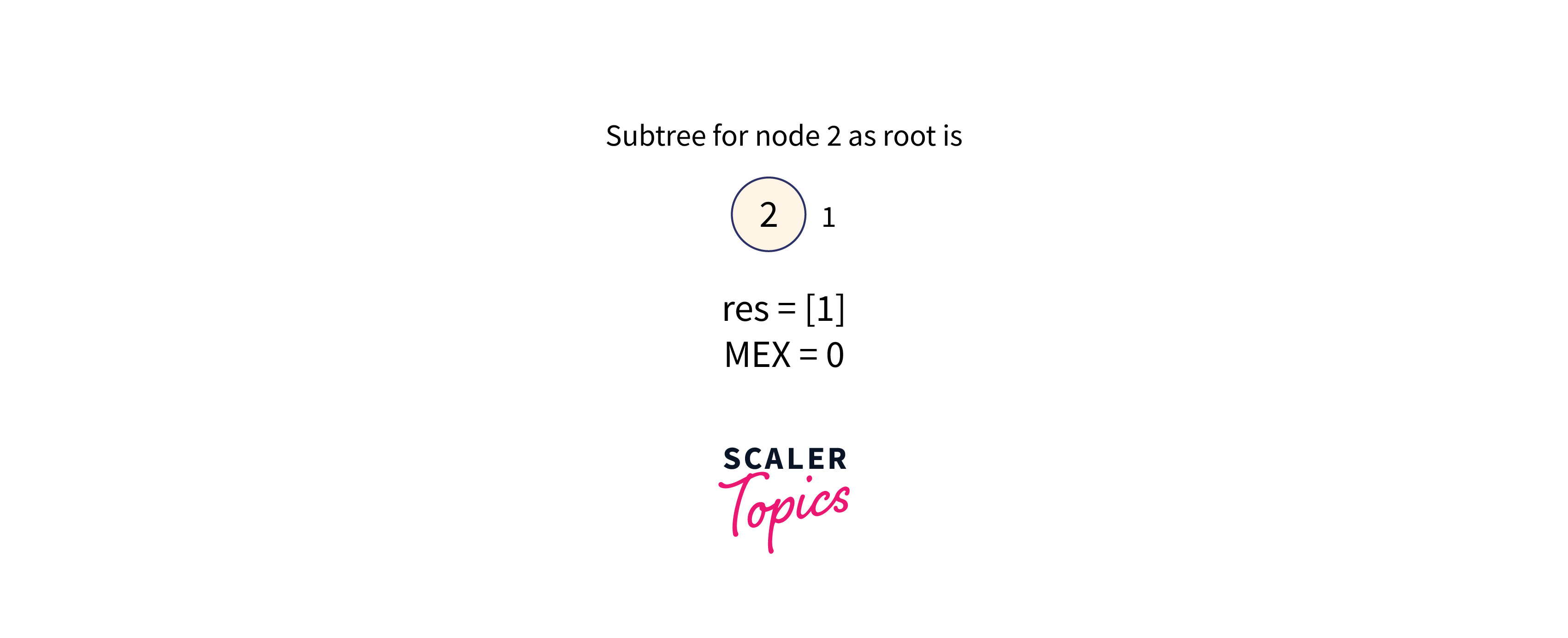
  The subtree of node 2 contains the value: [1], therefore the minimum missing number in the range is 0.

• For node 3:

  Subtree with node 3 as the root node is formed as shown in the below image:

  

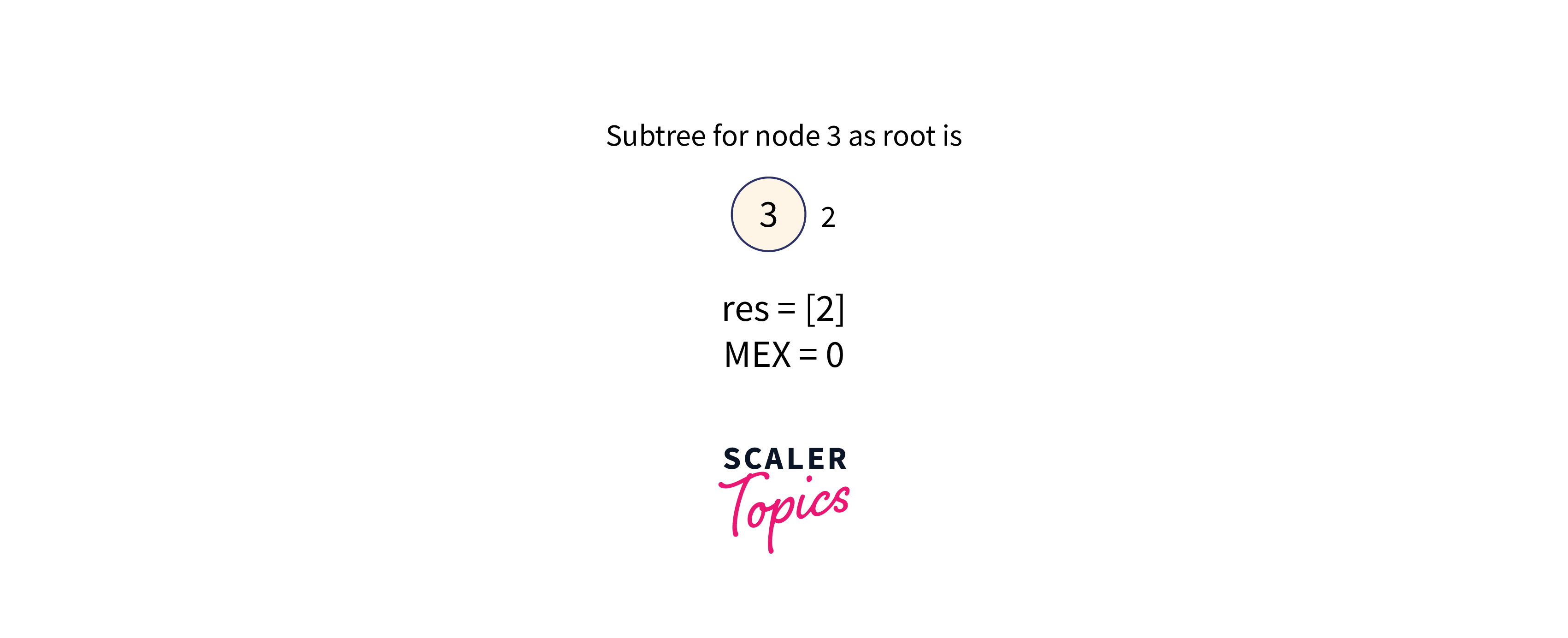
  The subtree of node 3 contains the value: [2], therefore the minimum missing number in the range is 0.

• For node 4:

  Subtree with node 4 as the root node is formed as shown in the below image:

  

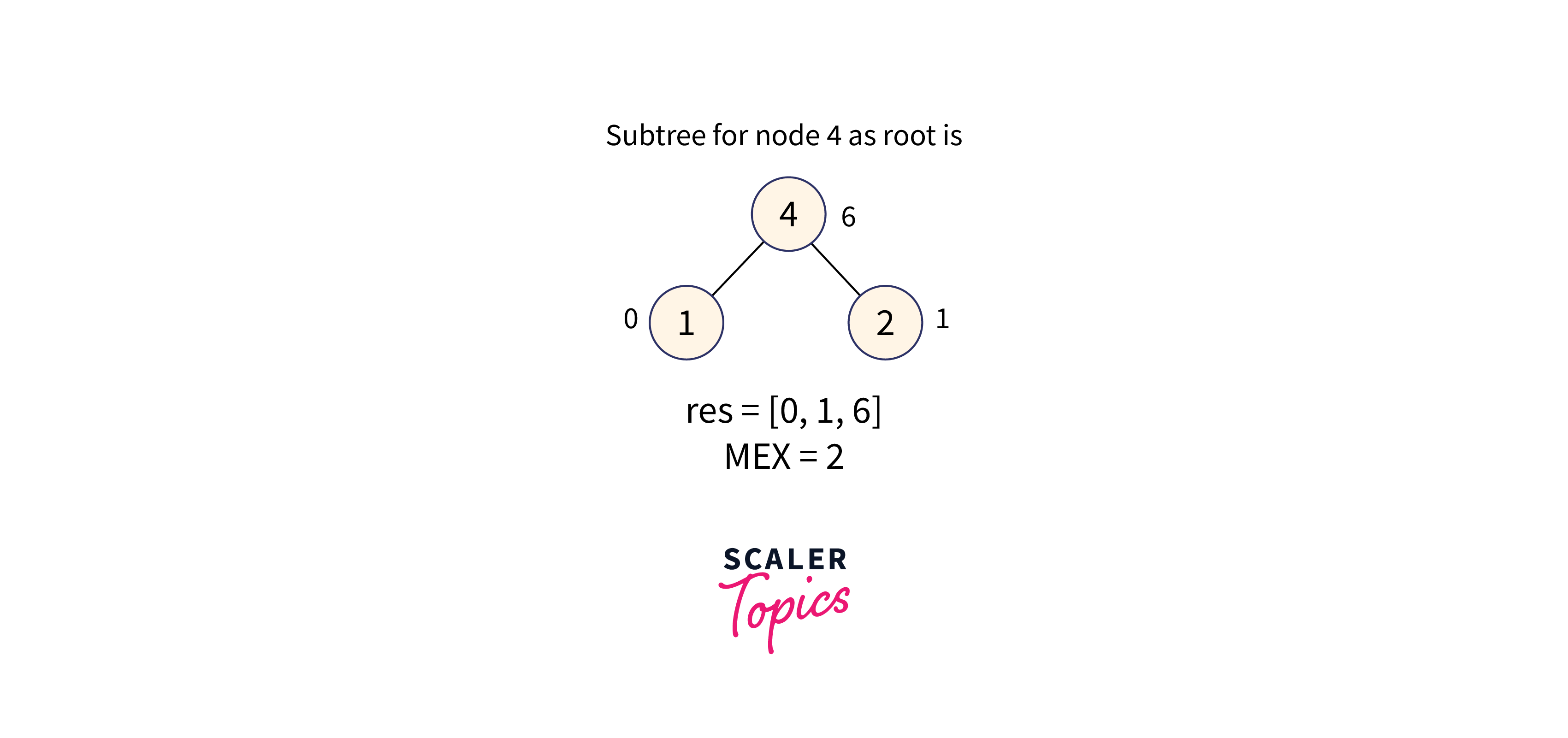
  The subtree of node 4 contains the values: [0, 1, 6], therefore the minimum missing number in the range is 2.

• For node 5:

  Subtree with node 5 as the root node is formed as shown in the below image:

  

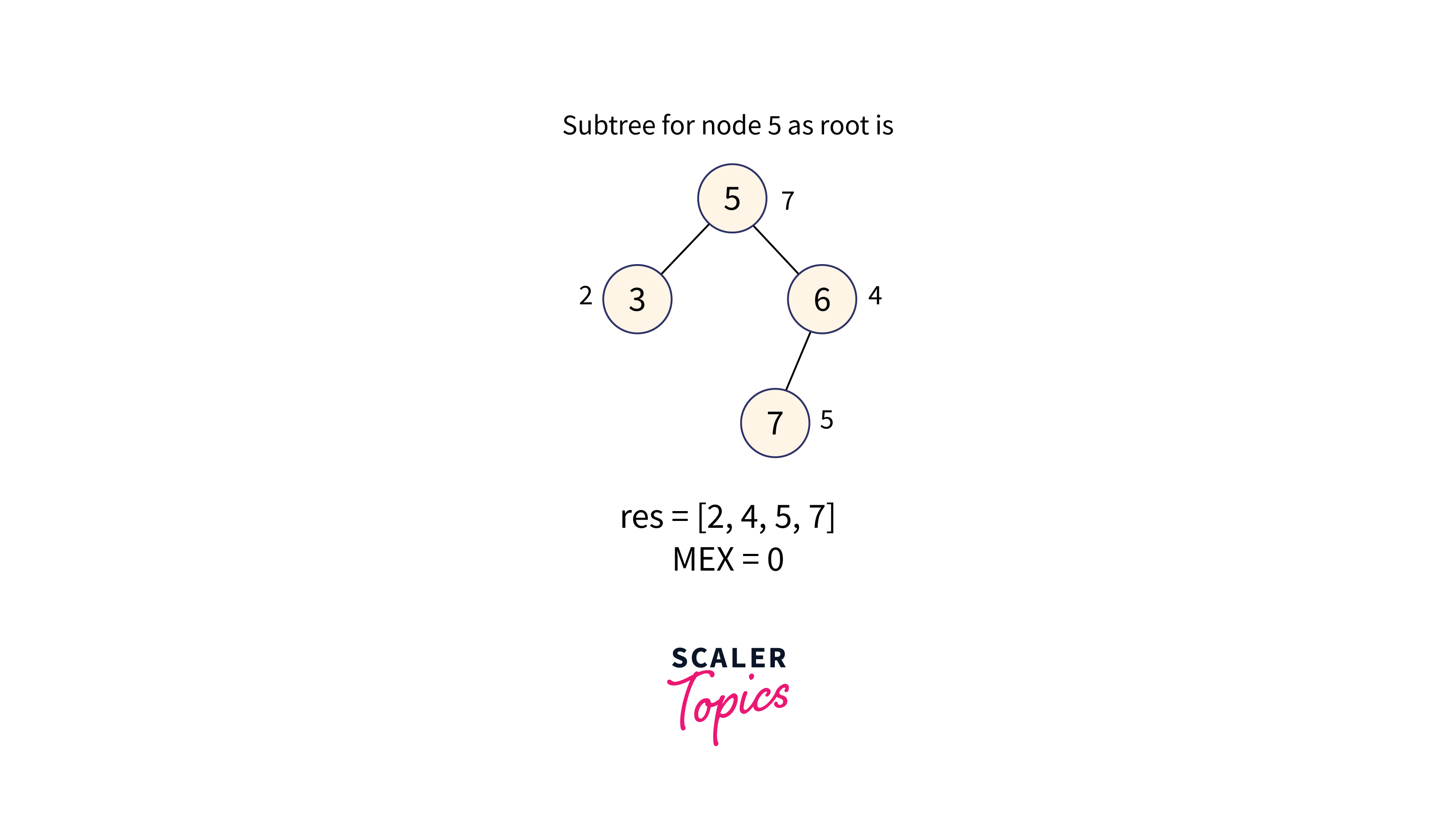
  The subtree of node 5 contains the values: [2, 4, 5, 7], therefore the minimum missing number in the range is 0.

• For node 6:

  Subtree with node 6 as the root node is formed as shown in the below image:

  

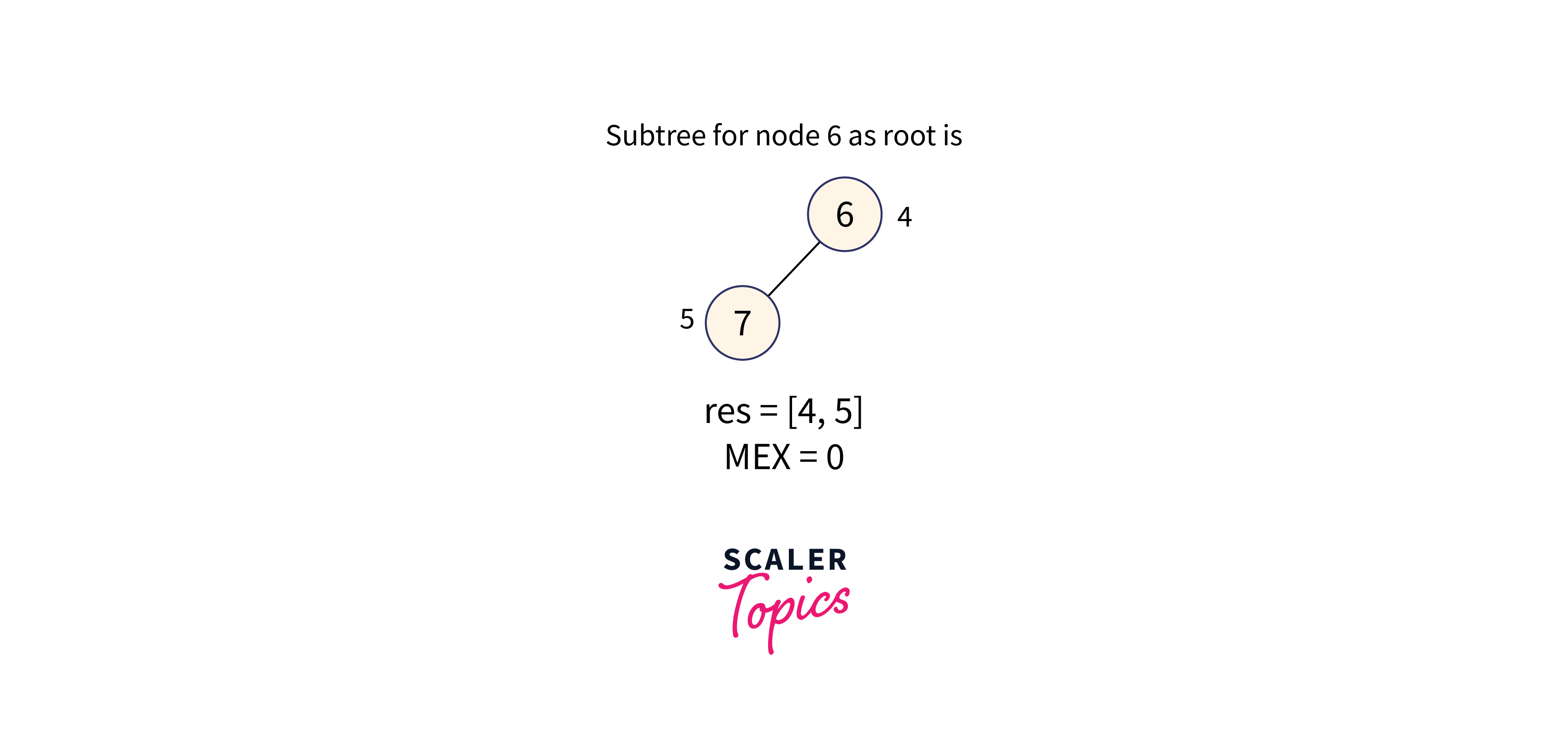
  The subtree of node 6 contains the values: [4, 5], therefore the minimum missing number in the range is 0.

• For node 7:

  Subtree with node 7 as the root node is formed as shown in the below image:

  

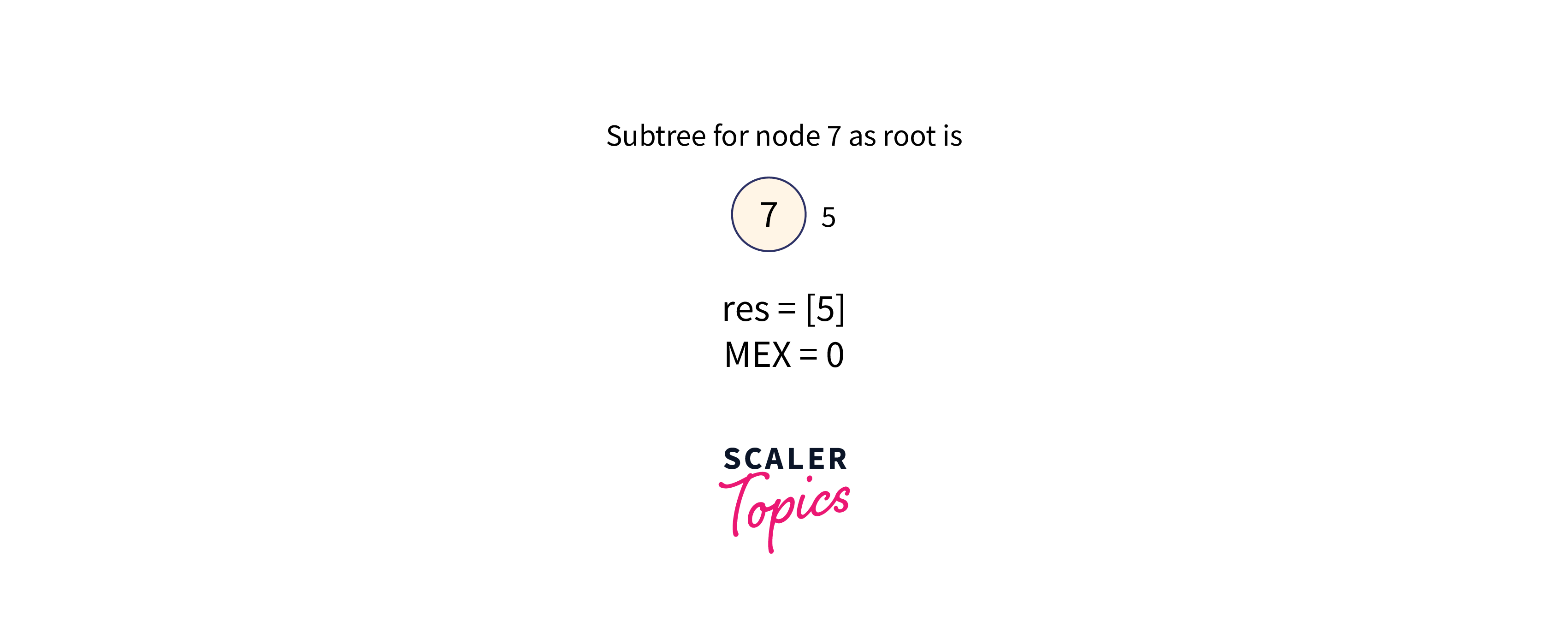
  The subtree of node 7 contains the value: [5], therefore the minimum missing number in the range is 0.

Therefore the output array obtained is [8, 1, 0, 0, 2, 0, 0, 0]

Example 2

For clear understanding, let's consider a skewed tree (A skewed binary tree is a type of binary tree in which all the nodes have only either one child or no child.) in the below example and find the MEX of every node in the tree:

Input:

value_arr : [4, 0, 2, 3, 1, 5]

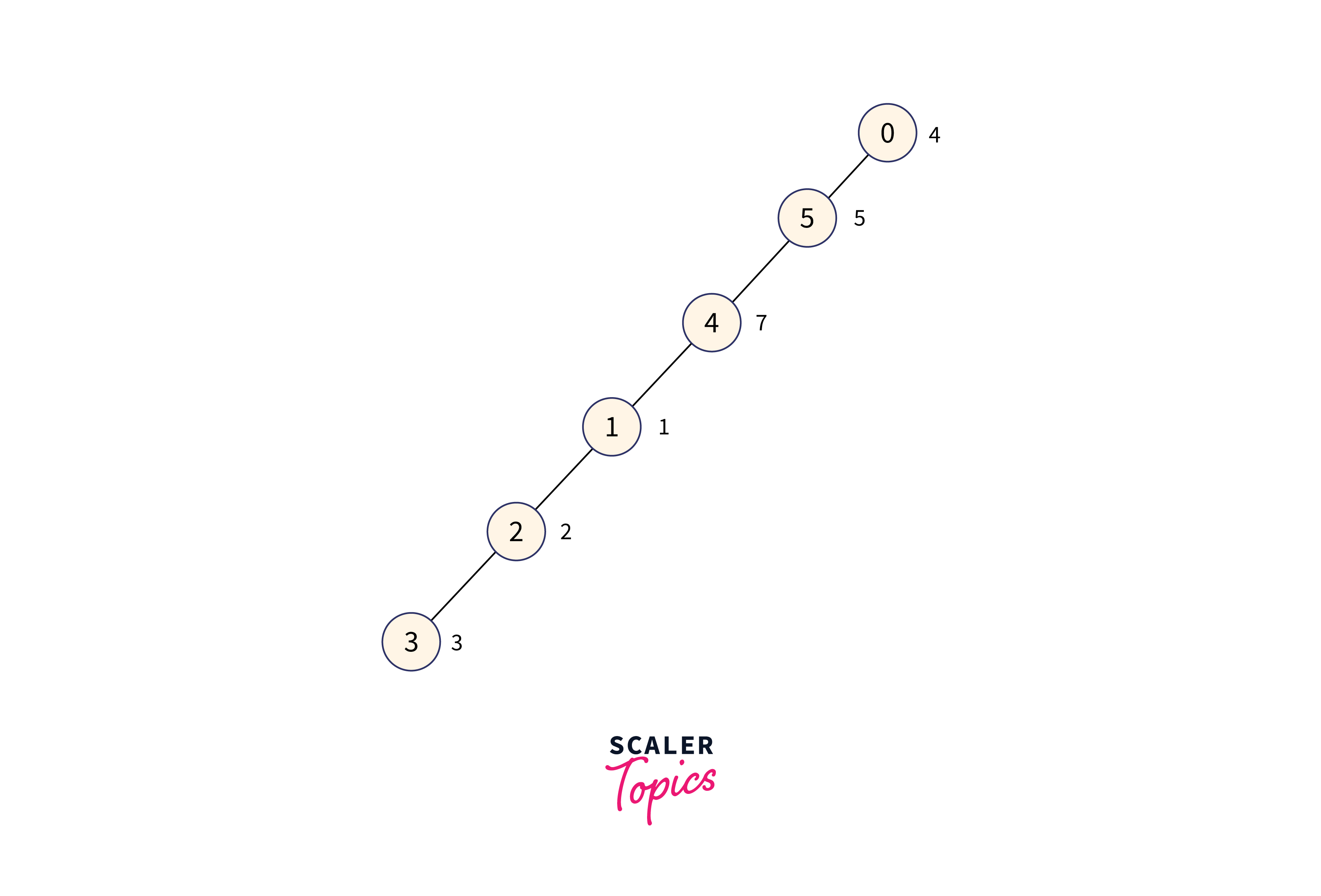
In the above example, every tree node's value is indicated corresponding to the node.

Output:

[6, 1, 0, 0, 4, 4]

Explanation:

The given tree has 6 nodes from the range [0, 5], and the values at each node are from the range [0, 5]. The below mentioned steps have to be performed to obtain value of MEX of every node in the tree:

• For node 0:

  Subtree with node 0 as the root node is formed as shown in the below image:

  

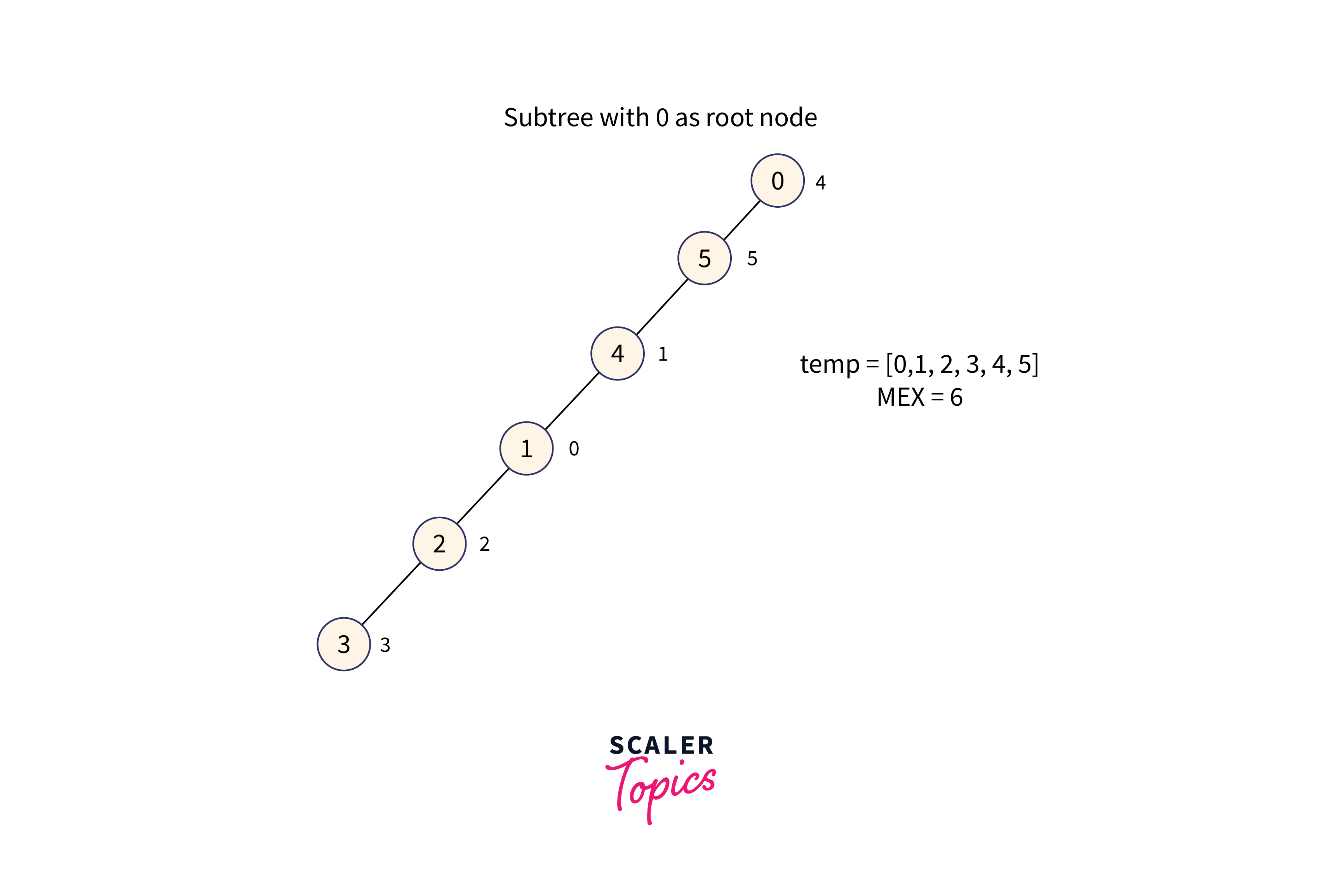
The subtree for node 0 contains values in the range [0, 5] therefore the minimum missing number is 6.

• For node 1:

  Subtree with node 1 as the root node is formed as shown in the below image:

  

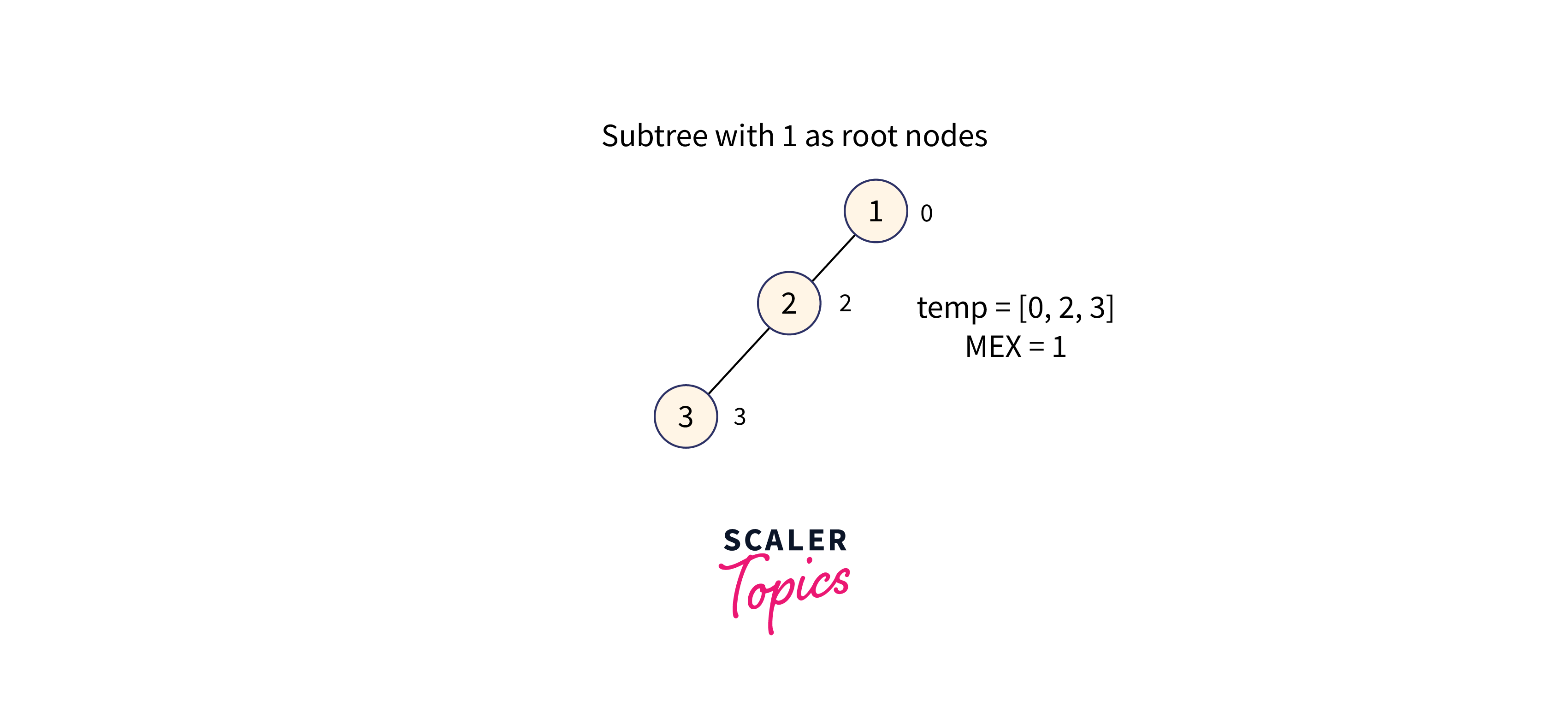
The subtree of node 1 contains the values: [0, 2, 3], therefore the minimum missing number in the range [0, 3] is 1.

• For node 2:

  Subtree with node 2 as the root node is formed as shown in the below image:

  

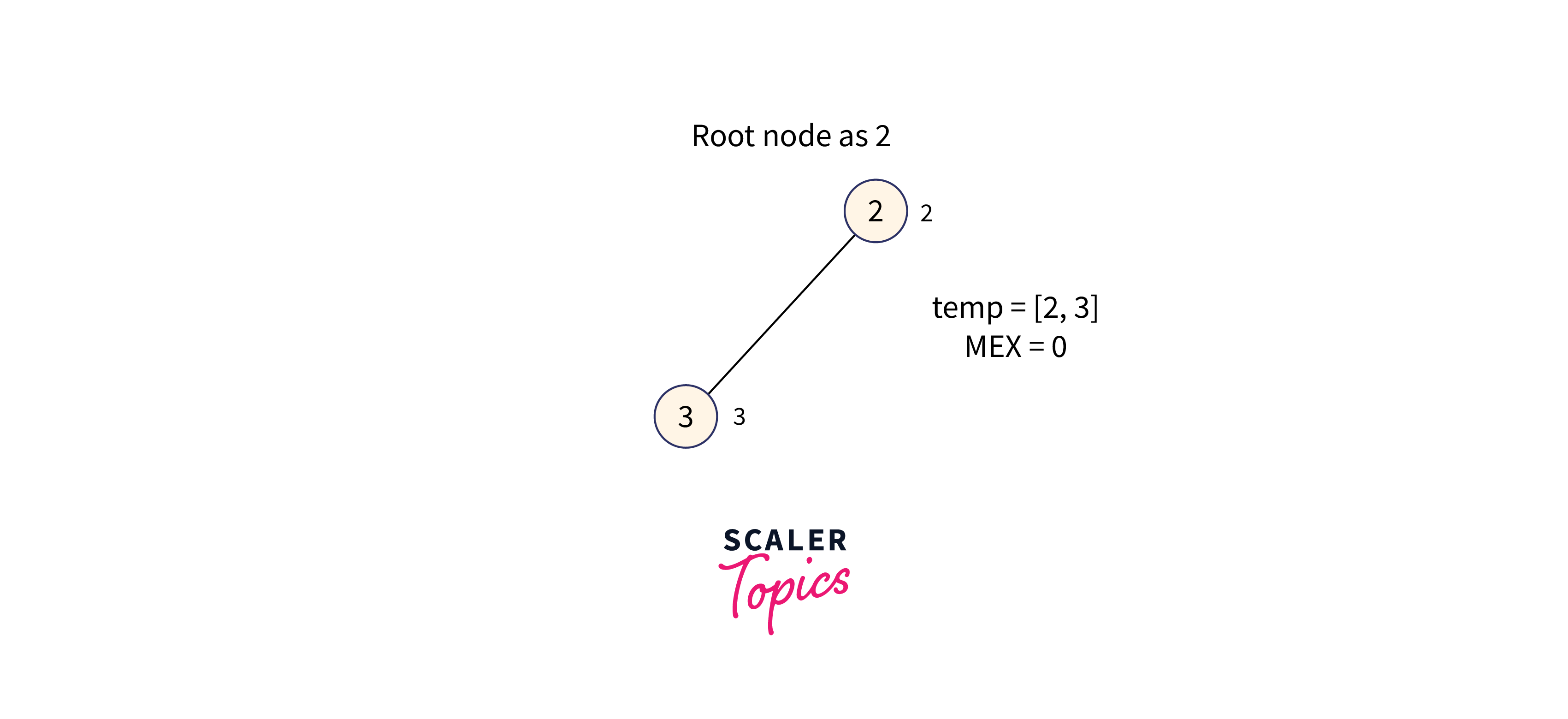
The subtree of node 2 contains the values: [2, 3], therefore the minimum missing number in the range [0, 3] is 0.

• For node 3:

  Subtree with node 3 as the root node is formed as shown in the below image:

  

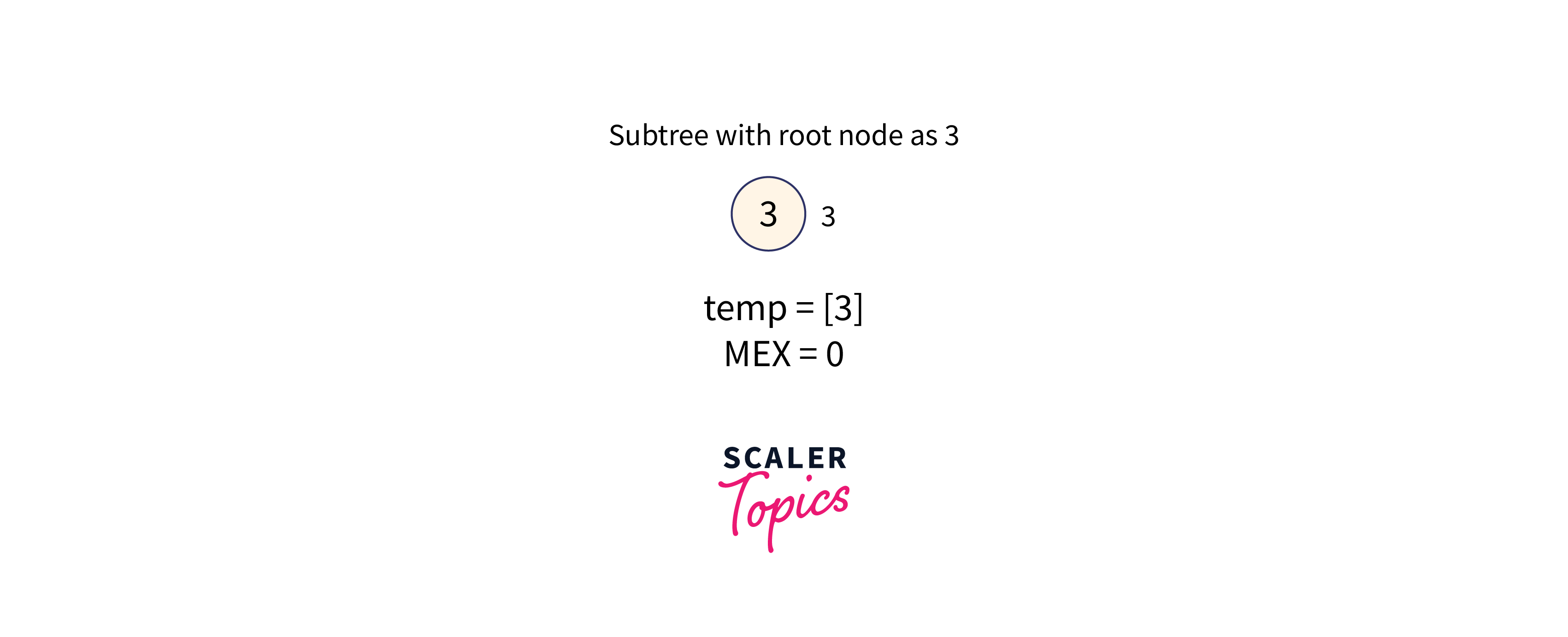
  The subtree of node 3 contains the value: [3], therefore the minimum missing number in the range [0, 3] is 0.

• For node 4:

  Subtree with node 4 as the root node is formed as shown in the below image:

  

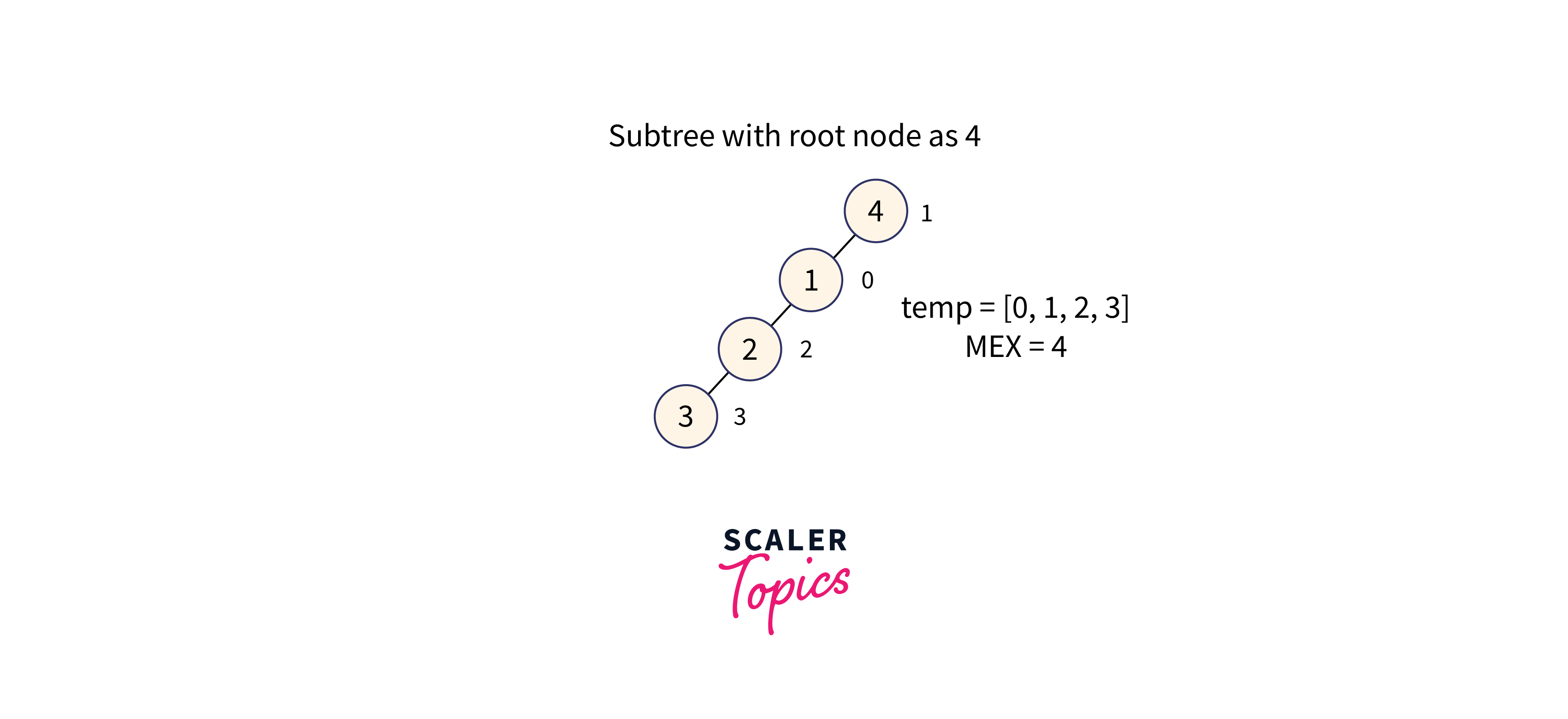
  The subtree of node 4 contains the values: [0, 1, 2, 3], therefore the minimum missing number in the range [0, 3] is 4.

• For node 5:

  Subtree with node 5 as the root node is formed as shown in the below image:

  

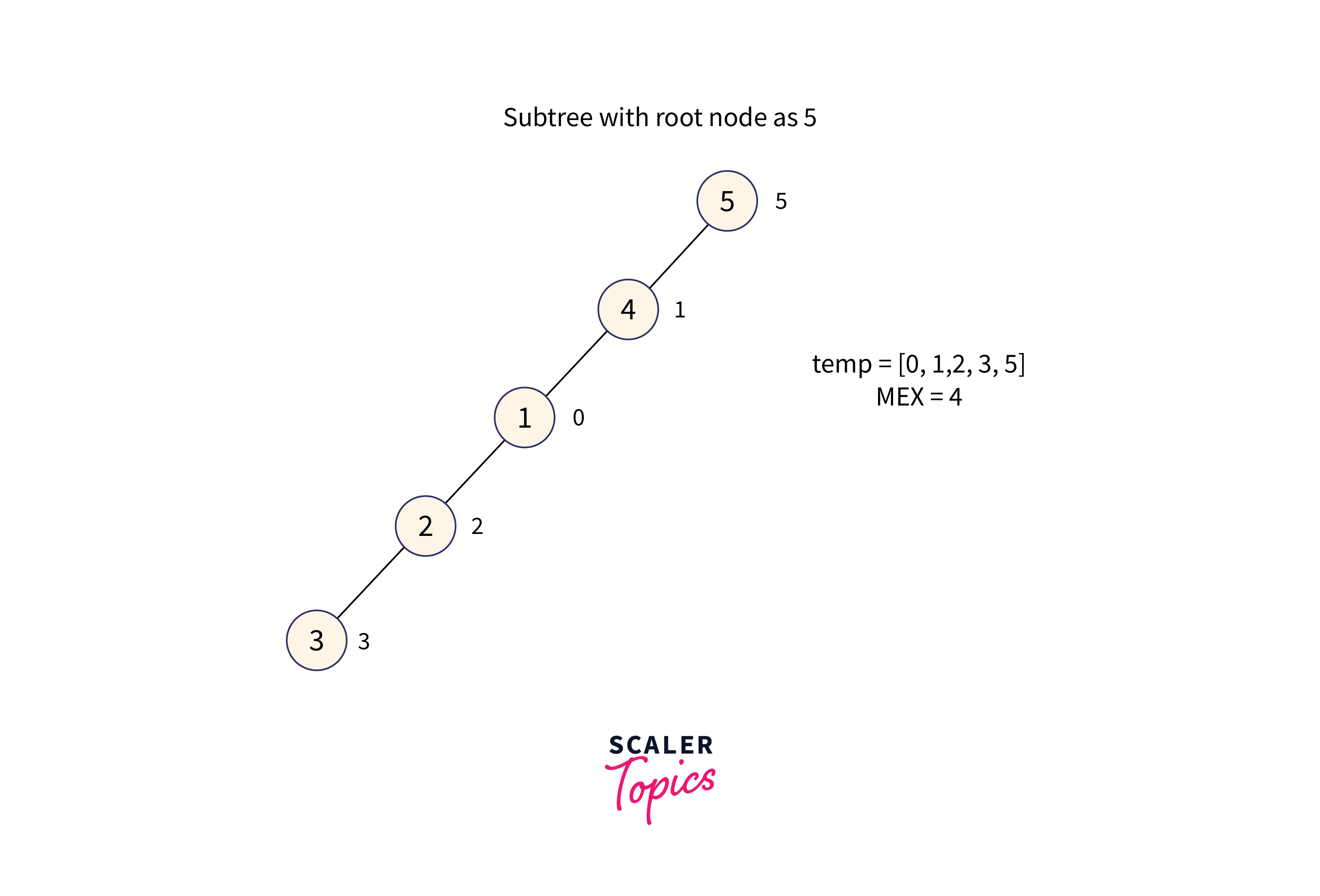
  The subtree of node 5 contains the values: [0, 1, 2, 3, 5], therefore the minimum missing number in the range [0, 5] is 4.

  Therefore the output array obtained is [6, 1, 0, 0, 4, 4].

Input

The input format of the tree, for finding the MEX in the tree during competitive programming and its corresponding node's value/weight is given as follows:

1. The First line consists of N, the number of nodes in the tree
2. The next line is an array of size N-1, where it consists of tuples of size 2 which indicates the edge present between the two nodes in the tuple.
3. The last line consists of a value/weight array that has the values of each node's corresponding value/weight.

Output

The output format consists of an array where it has the value of MEX of each node of the given tree. Find the value of MEX of every node and return them as an array.

Constraints

• $1 <= N <=10^5$
• $0 <=$u_i$,$v_i$<= N-1$
• $u_i$ is never equal to $v_i$
• $0 <= value[i] <= N-1$

Here N represents the number of nodes in the tree and u, and v represents the nodes of the given tree.

Approach

Each node's MEX value is to be added in the array and that array has to be returned to the main function. In the given problem, so we traverse the complete tree using DFS (Depth First Search Algorithm). Our task mainly here is every DFS function call returns a sorted merged temporary array which has the values of all the nodes present in the particular node's subtree. In this sorted merged array, we need to find the minimum element which is missing in the range [0, Number of nodes in tree] using the binary search algorithm. It is because the binary search algorithm takes O(log N) as compared to other searching techniques, but since this can be applied only on sorted arrays we merge the temporary array at each DFS call for every node in a sorted fashion and find the smallest missing positive number from that array. Here only DFS is applied because it explores as far as possible along each branch. It traverses to the deepest node possible and adds the node's corresponding weight to the temporary array. As soon as the DFS function call returns the temporary array, we apply Binary Search on it to find the MEX of that particular node.

Algorithm

The algorithm for finding the MEX of each node in the given tree is as follows:

• Firstly we need to initialize the answer array where we will be storing the MEX value for every node from the given tree.
• Our second step involves performing DFS starting from node 0 i.e, the root node of the tree. In the DFS algorithm we follow the below-mentioned steps:
  • We store all the node's values that are present corresponding to the node in the temporary array of size equal to the number of nodes present in the subtree of the node which is considered.
  • The next step includes merging the temporary array of one node to the other node's temporary node(left and right node of the root) during the DFS traversal.
  • This merging is performed in a sorted manner so that we can search for the smallest missing element in the sorted merged order using the binary search algorithm. Here binary search algorithm is used to find the smallest positive missing from the range of temporary array's values.
• For every node we perform the binary search on the temporary array for that present/ current node or a subtree to find the MEX and store it in the array answer.
• We finally print the MEX of each node from the answer array.

Implementation

Below is the implementation of the above approach for finding the MEX of every node in the given tree in C++, and Java. Many recursive calls in python make it hard to keep track of return values in each recursive call so we generally don't prefer python for this approach.

C++ program for finding the MEX for every node in the given tree:

Output

[7, 1, 0, 1, 0, 1, 0]

Java program for finding the MEX for every node in the given tree:

Output

[7, 1, 0, 1, 0, 1, 0]

Explanation:

The given tree has 7 nodes and the values of the nodes are in the range [0, 6]. MEX obtained for every node is explained below. The given tree is as follows:

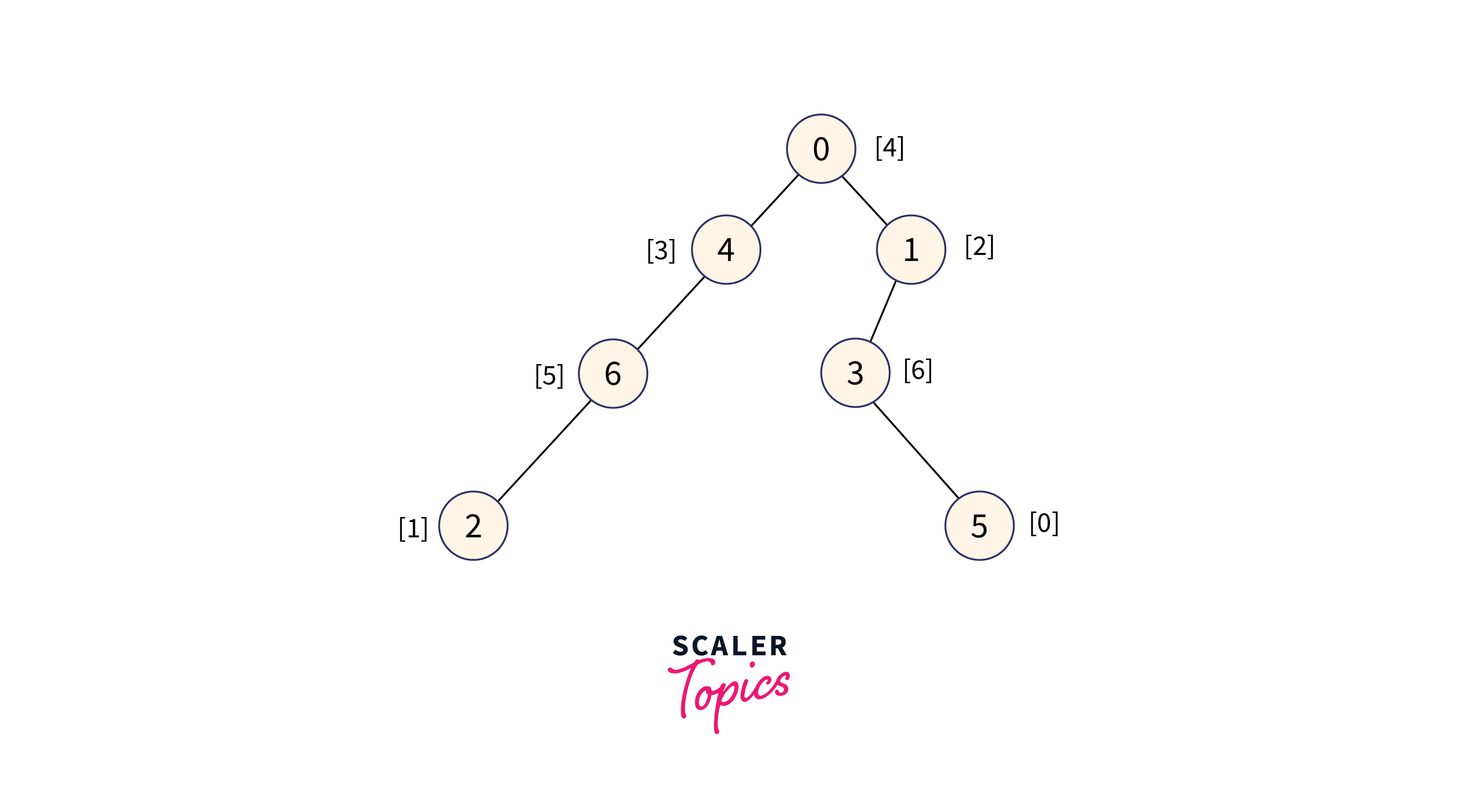
The given value array is: [4, 2, 1, 6, 3, 0, 5]

• After performing the DFS on Node 0, we get all the merged values of weights from all its nodes in the subtree where Node 0 is the root node for that subtree, then we apply binary search on that sortedly merged array.

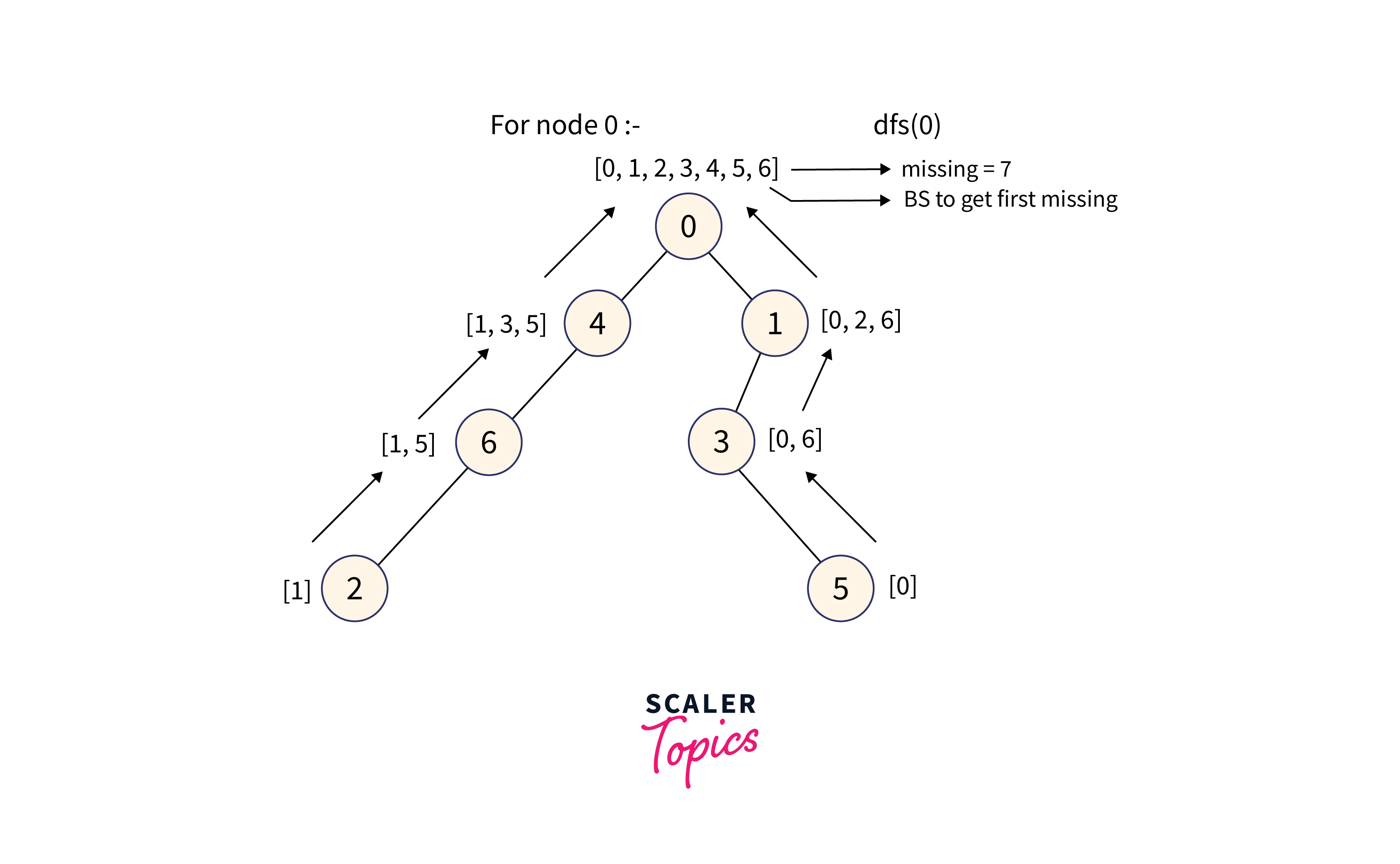  Follow below steps to find the value of MEX of every node in the tree:

  The subtree with 0 as the root node contains all the values in the range [0, 6] therefore the minimum missing number is 7.

• For node 1:

  DFS performed on Node 1's subtree to get the sortedly merged values of weights in the subtree. To find the MEX value, perform binary search on that array.

  

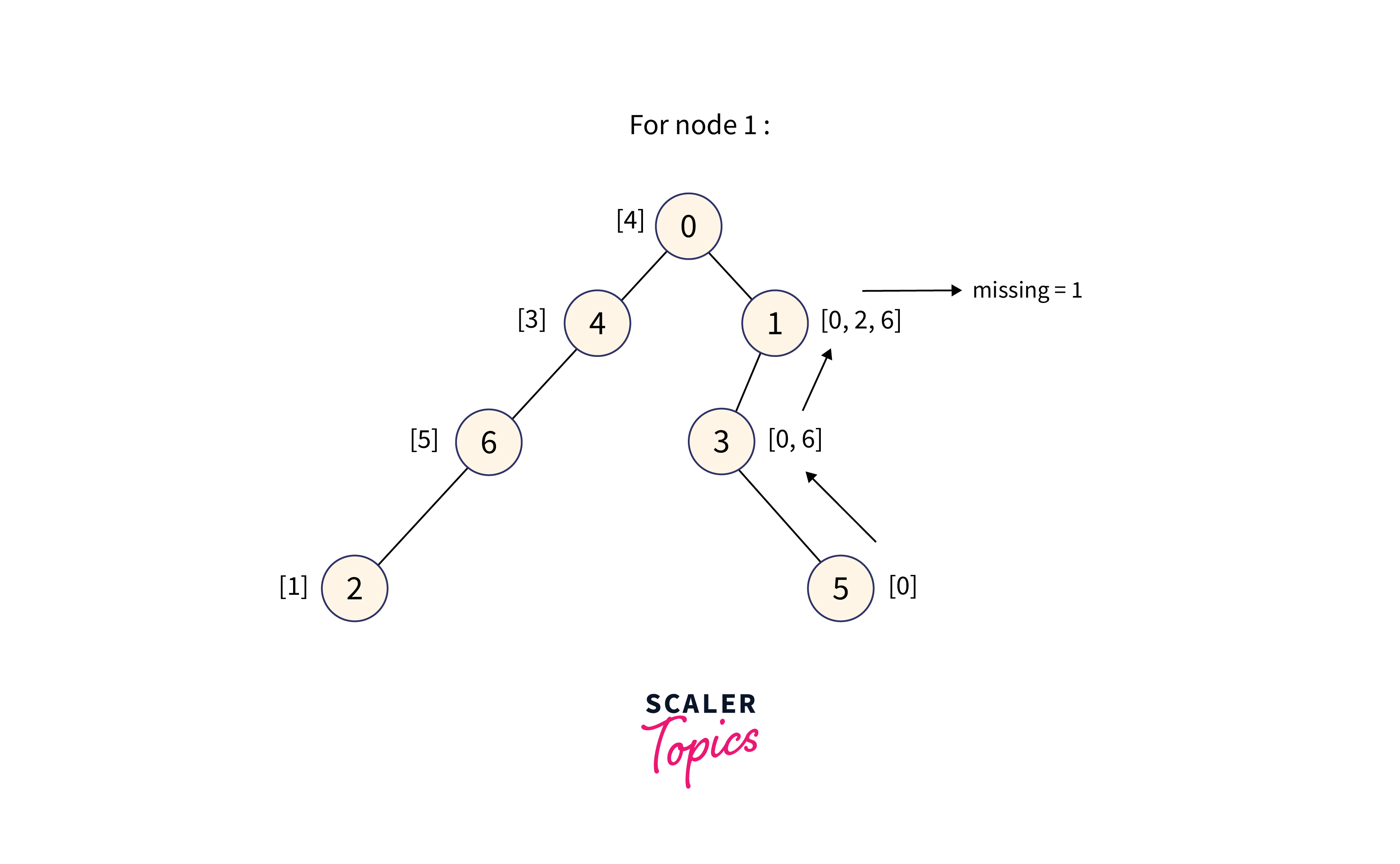
  The subtree of node 1 contains the values: [0, 2, 6], therefore the minimum missing number in the range is 1.

• For node 2:

  DFS performed on Node 2's subtree to get the sortedly merged values of weights in the subtree. To find the MEX value, perform binary search on that array.

  

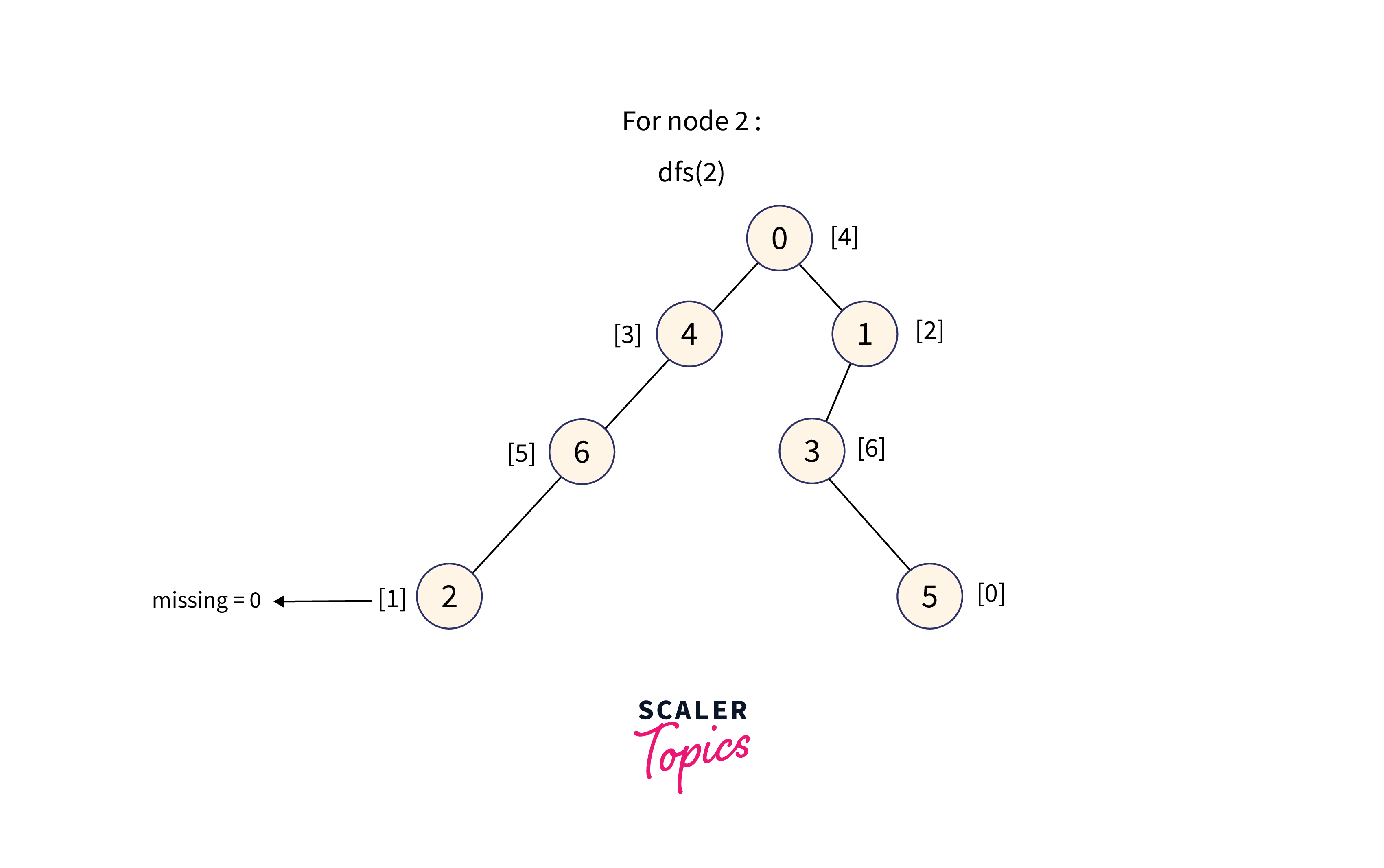
  The subtree of node 2 contains the value: [1], therefore the minimum missing number in the range is 0.

• For node 3:

  DFS performed on Node 3's subtree to get the sortedly merged values of weights in the subtree. To find the MEX value, perform binary search on that array.

  

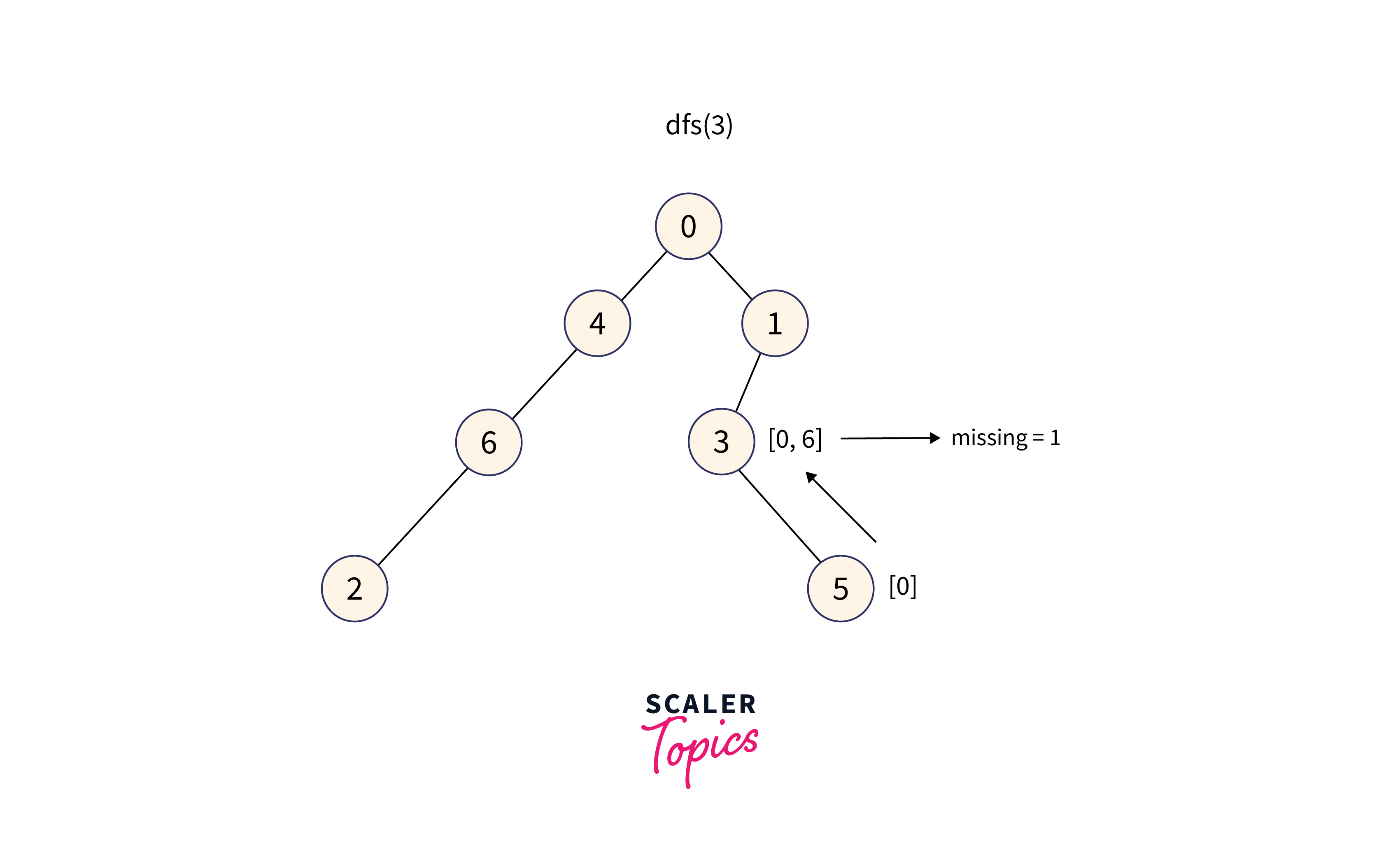
  The subtree of node 3 contains the values: [0, 6], therefore the minimum missing number in the range is 1.

• For node 4:

  DFS performed on Node 4's subtree to get the sortedly merged values of weights in the subtree. To find the MEX value, perform binary search on that array.

  

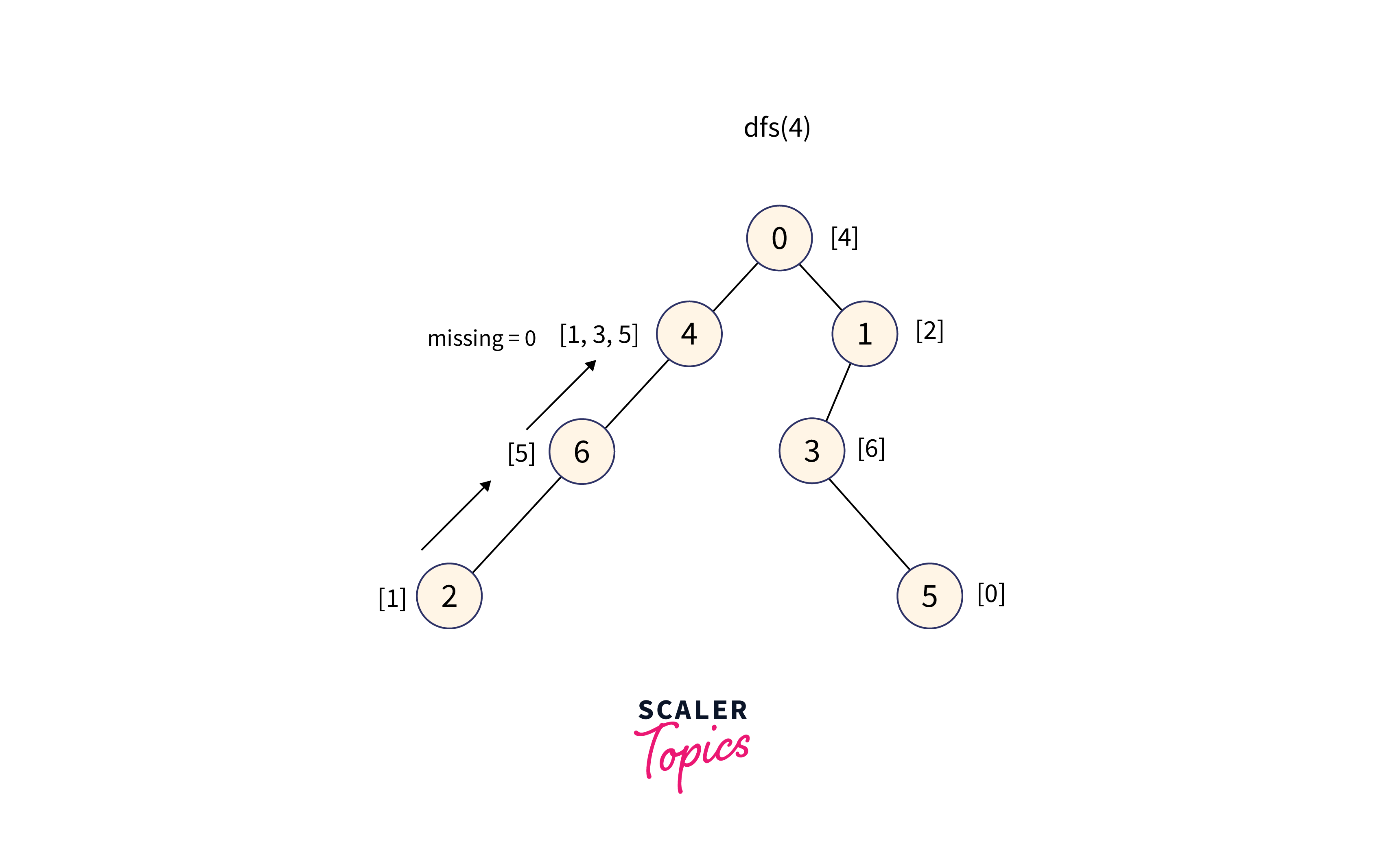
  The subtree of node 4 contains the values: [1, 3, 5], therefore the minimum missing number in the range is 0.

• For node 5:

  DFS performed on Node 5's subtree to get the sortedly merged values of weights in the subtree. To find the MEX value, perform binary search on that array.

  

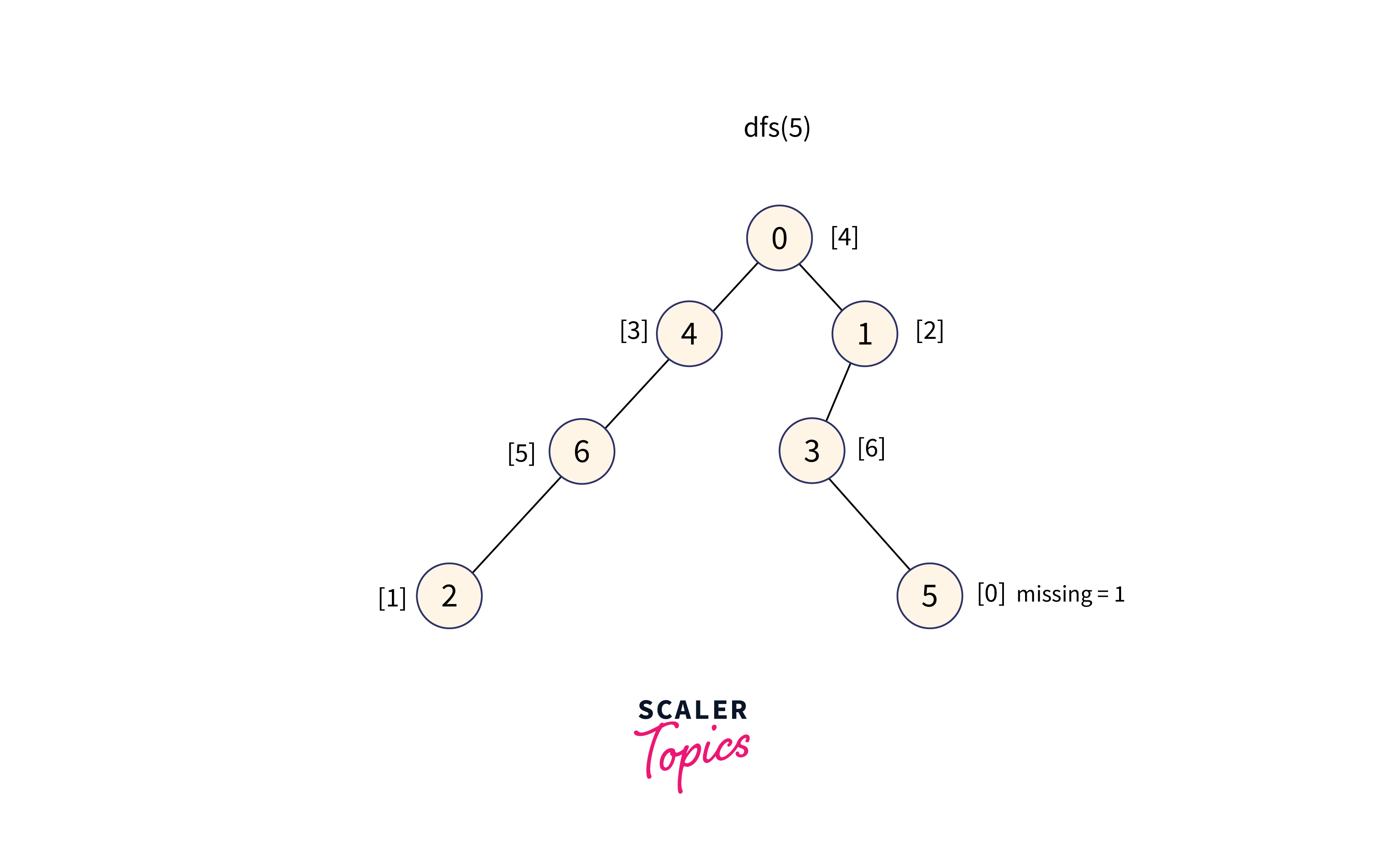
The subtree of node 5 contains the value: [0], therefore the minimum missing number in the range is 1.

• For node 6:

  DFS performed on Node 6's subtree to get the sorted merged values of weights in the subtree. To find the MEX value, perform a binary search on that array.

  

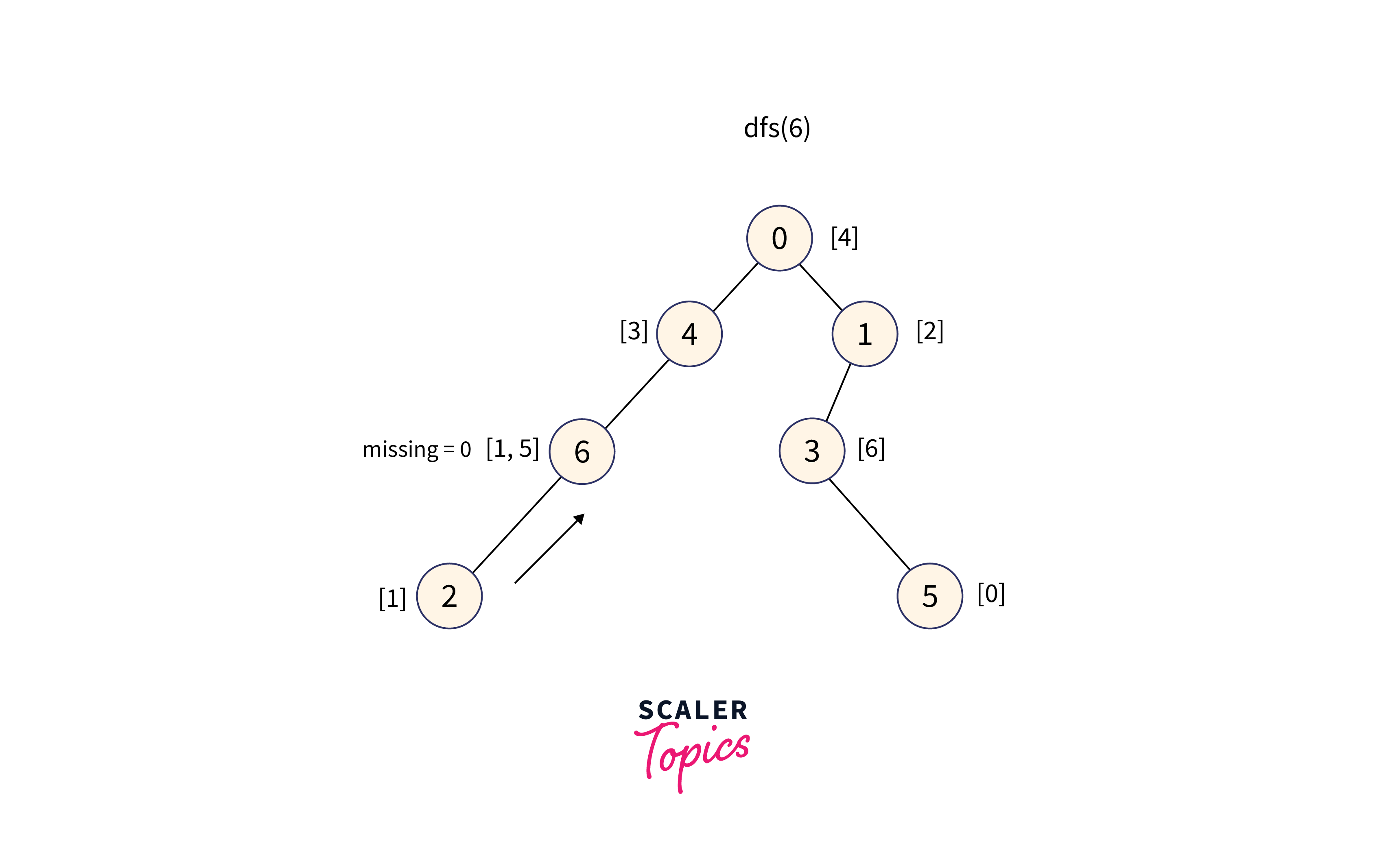
  The subtree of node 6 contains the values: [1, 5], therefore the minimum missing number in the range is 0.

  Therefore the output ans array is as [7, 1, 0, 1, 0, 1, 0]

Complexity Analysis

Time complexity: O(N(N + log N)), where N represents the number of nodes in the given tree.

• For every node, a binary search is performed to find the minimum positive element so its time complexity is O(log N)
• For every node in the tree, DFS(Depth First Search) is called which has the time complexity of O(N). If the entire tree is traversed, the temporal complexity of DFS is O(N), where N is the number of nodes of the trees.
• Therefore the overall time complexity for finding the MEX of every node in the given tree is O(N(N + log N))

Space complexity: O(N), where N represents the number of nodes in the given tree.

• Extra space is for storing the answer array and also is required for the auxiliary stack space in the recursive calls within the program. So at any time maximum number of recursive calls is N.