Introduction to Geometric Deep Learning

What is Geometric Deep Learning?

Deep learning, a subfield of machine learning, has been extremely successful in a wide range of applications, such as image and speech recognition, natural language processing, and so on. However, it mainly focuses on grid-like structured data such as images, videos, and signals that a tensor can represent. But many real-world data do not have a grid-like structure, such as graphs, point clouds, and manifolds. These data types are commonly found in various fields, such as chemistry, physics, biology, and social networks.

Geometric deep learning aims to extend deep learning techniques to non-Euclidean structured data such as graphs, point clouds, and manifolds. This involves the development of neural networks that can operate on data with irregular or non-grid-like structures and the design of loss functions and architectures that are appropriate for these types of data.

For example, in computer vision, 3D point clouds represent objects in the real world. Still, traditional convolutional neural networks (CNNs) designed to operate on grid-like data, such as images, cannot be directly applied to point clouds. In this case, geometric deep learning techniques can design CNNs operating on 3D point clouds.

How Geometric Deep Learning applied in NLP?

Geometric deep learning can be applied in natural language processing (NLP) in several ways. One of the main ways is by using graph-based models to represent and analyze text data. Here are a few examples of how deep geometric learning can be applied in NLP:

• Text classification:
  Graph-based models can represent text data as a graph, where each node represents a word or a sentence and edges represent the relationships between words or sentences. These models can then be used for text classification tasks like sentiment analysis and topic classification.
• Language modeling:
  Graph-based models can be used to model the underlying structure of natural languages, such as the dependencies between words in a sentence. This can improve language modeling tasks, such as translation and text generation.
• Text summarization:
  Graph-based models can summarize a given text by identifying the most important sentences or paragraphs and condensing them into shorter ones.
• Named Entity Recognition:
  Graph-based models can identify and classify named entities, such as people, organizations, and locations, in text data.
• Sentence embedding:
  Graph-based models can embed sentences, paragraphs, or even documents into a low-dimensional vector space, which can then be used as input for downstream NLP tasks such as text classification or clustering.

Categories of Geometric Deep Learning

Geometric deep learning can be broadly categorized into two main categories:

1. Graph Neural Networks (GNNs):
   These are neural networks designed to operate on graph-structured data, such as social networks, molecular graphs, and road networks. GNNs are typically based on message-passing algorithms, where the nodes in the graph pass messages to their neighboring nodes. These algorithms are designed to capture the graph's local and global structural information. Examples of GNNs include Graph Convolutional Networks (GCNs) and Graph Attention Networks (GATs).
2. Manifold-valued Neural Networks (MVNs):
   These are neural networks designed to operate on data on a non-Euclidean manifold, such as images on a sphere, signals on a torus, and 3D point clouds. MVNs are typically based on geometric deep learning frameworks, where the neural networks are designed to respect the geometric structure of the manifold. Examples of MVNs include Spherical CNNs and PointNet.

Both GNNs and MVNs can learn features that reflect the underlying geometric structure of the data, which is important for many applications, such as image classification, object detection and segmentation, natural language processing, and recommendation systems.

Another category that can be considered as a part of geometric deep learning is Topology and Shape Analysis which deals with the analysis of topological and geometric properties of data, such as connectivity, homology, and curvature, and is used in fields such as computer vision, medical imaging, and computational biology.

In summary, geometric deep learning can be broadly categorized into Graph Neural Networks (GNNs) and Manifold-valued Neural Networks (MVNs), designed to operate on graph-structured and manifold-valued data. Another category that can be considered a part of geometric deep learning is Topology and Shape Analysis which deals with analyzing topological and geometric data properties.

Fundamental Underlying Building Blocks

There are several fundamental building blocks commonly used in deep geometric learning:

They are based on the convolution operation, which combines information from neighboring nodes in a graph.

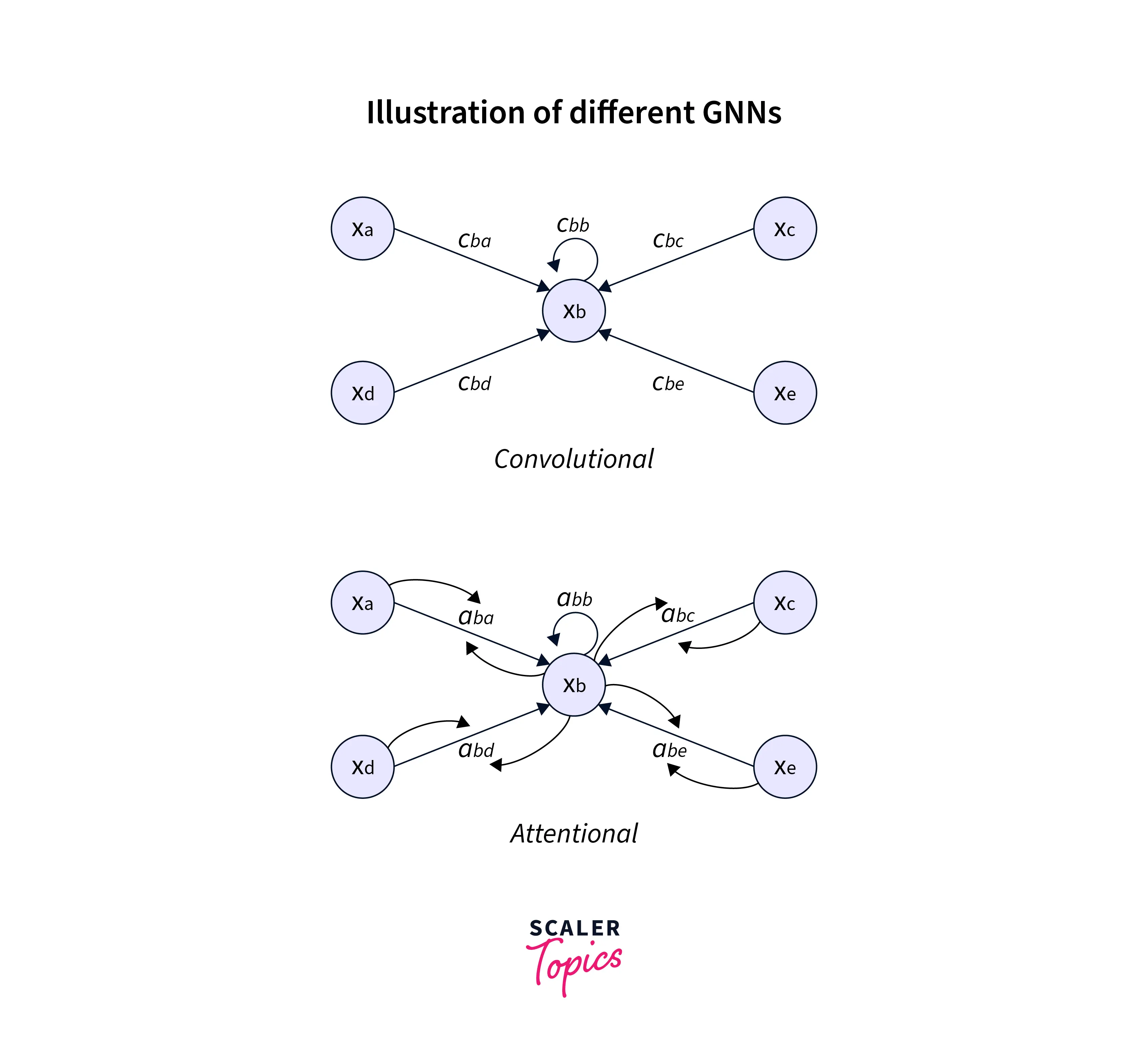
• Graph Convolutional Networks (GCNs):
  GCN is a type of neural network that can be used to classify and extract features from graph-structured data. They are based on the convolution operation, which combines information from neighboring nodes in a graph.
• Graph Attention Networks (GATs):
  GATs are a variant of GCNs that use attention mechanisms to weigh the importance of different nodes in a graph. This allows GATs to focus on the most relevant nodes while processing the graph.
• Laplacian Eigenmaps:
  It is a technique used to reduce the dimensionality of graph-structured data by mapping it to a lower-dimensional space. This is done by finding the eigenvectors of the Laplacian matrix of the graph.
• Spectral Graph Convolution:
  It is a technique for processing graph-structured data based on the graph Laplacian's eigenvectors. It allows convolving of a signal on the graph by applying a filter in the Fourier space.
• Differentiable Pooling:
  It is a method that dynamically adjusts the number of nodes in a graph during the training process, which allows for tackling variable-size graph-structured data.
• Graph Capsules:
  It is a method that aims to improve the performance of graph-based models by using a capsule network architecture. Capsules are a type of neural network that can model relationships between objects.
• Attention mechanism:
  It is a technique used to weigh the importance of different parts of an input when processing it. Attention mechanisms can be used to selectively focus on the most relevant nodes in a graph when processing it.

These building blocks help handle the irregular data structure and improve the model's performance on geometric deep-learning tasks.

Examples of Geometric Deep Learning

Geometric deep learning is a field that combines the power of deep learning with the ability to handle non-Euclidean data, such as graphs, manifolds, and other structured data. Some examples of tasks that fall under the purview of geometric deep learning include:

• Graph classification and Graph convolutional networks.
• Point cloud analysis.
• Manifold learning.
• Hyperbolic geometry and tree-structured data.
• Riemannian geometry and sensor data.

These are just a few examples, but many other types of structured data and tasks can be tackled with geometric deep learning.

Molecular Modeling and Learning

Molecular modeling and learning is an area of research in which geometric deep-learning techniques are used to analyze and predict the properties of molecules. This research aims to develop machine learning models that can accurately predict the properties of molecules, such as their stability, reactivity, and toxicity, based on their 3D structure.

One of the main challenges in this area is that molecules have complex and irregular structures, making applying traditional machine-learning techniques difficult. Geometric deep learning approaches are well suited to this task because they can operate on non-Euclidean structured data, such as graphs.

One popular approach in molecular modeling and learning is using graph convolutional neural networks (GCNs) to predict the properties of molecules. A molecule can be represented as a graph where atoms are the nodes, and chemical bonds are the edges. GCNs can extract features from the molecular graph that are relevant for predicting the molecule's properties.

Another approach is using point cloud representation for molecular modeling, where a molecule is represented as a set of 3D points, and neural networks such as PointNet or PointNet++ are used to extract features from the point cloud.

In addition to GCNs and PointNet, other techniques, such as graph attention networks (GATs) and graph auto-encoders (GAEs), have been used in molecular modeling and learning to analyze and predict the properties of molecules.

3D Modeling and Learning

3D modeling and learning is an area of research in which geometric deep learning techniques are used to analyze and generate 3D shapes and scenes. This research aims to develop machine learning models that can accurately predict objects' shape, pose, and motion in a 3D scene and generate new 3D shapes and scenes based on a given input.

One of the main challenges in this area is that 3D shapes and scenes have complex and irregular structures, which makes it difficult to apply traditional machine-learning techniques. Geometric deep learning approaches are well suited to this task because they can operate on non-Euclidean structured data, such as point clouds and graphs.

One popular approach in 3D modeling and learning is using point cloud convolutional neural networks (PointCNNs) to predict objects' shape, pose, and motion in a 3D scene. A 3D shape can be represented as a point cloud, and PointCNNs can be used to extract features from the point cloud that are relevant for predicting the object's shape, pose, and motion.

Another approach is using graph representation for 3D modeling, where a 3D shape is represented as a graph where the nodes are points and edges are the connections between the points. Graph neural networks (GNNs) such as Graph Convolutional Networks (GCNs) or Graph Attention Networks (GATs) are used to extract features from the graph that are relevant for predicting the shape, pose, and motion of the object.

In addition to PointCNNs and GNNs, other techniques, such as graph auto-encoders (GAEs) and manifold-valued neural networks (MVNs), have been used in 3D modeling and learning to analyze and generate 3D shapes and scenes.

The Curse of Dimensionality

In geometric deep learning, the curse of dimensionality refers to the fact that as the dimensionality of the input data increases, the amount of data required to model the data accurately also increases exponentially. This can make it difficult to train deep learning models on high-dimensional data such as 3D point clouds and graphs.

For example, when working with 3D point clouds, the number of points in the cloud can be very large, and each point can have many features, such as position, normal, and color. This results in high-dimensional input space, making it difficult to train deep-learning models on the data.

Similarly, when working with graphs, the number of nodes and edges in the graph can be very large, and each node and edge can have many features. This results in high-dimensional input space, making it difficult to train deep-learning models on the data.

The curse of dimensionality can also occur when working with other types of non-Euclidean structured data, such as images on a sphere or signals on a torus.

To mitigate the curse of dimensionality in geometric deep learning, dimensionality reduction techniques such as PCA and Autoencoder can be used to project high-dimensional data onto a lower-dimensional subspace or learn a lower-dimensional representation of the data, making it easier to train deep learning models on the data. Additionally, various techniques such as graph-pooling and graph-coarsening can be used to tackle this problem.

Here is an example of how PCA can be implemented in Python using the sci-kit-learn library:

Another technique is autoencoder, which is a neural network that is trained to reconstruct its input. Autoencoder can be used for dimensionality reduction by training it to reconstruct the input data from a lower-dimensional bottleneck representation.

Here is an example of how an autoencoder can be implemented in Python using the Keras library:

Importing Library

• The code first imports the necessary modules from the Keras library: the Input and Dense layers and the Model class.

Define the Input Layer

• Then, it defines an input layer with a shape of (original_dim,), where original_dim is a user-defined variable. This input layer is used as the input for the autoencoder.

Define the Bottleneck Layer

• Next, a bottleneck layer is defined using the Dense layer, with a dimensionality of bottleneck_dim and a ReLU activation function. The bottleneck layer is used to reduce the dimensionality of the input data.

Define the Reconstruction Layer

• Then, a reconstruction layer is defined using the Dense layer, with a dimensionality of original_dim and a sigmoid activation function. The reconstruction layer is used to reconstruct the original data from the bottleneck representation.

Create the Autoencoder Model

• The autoencoder is then created by connecting the input layer to the reconstruction layer using the Model class.

Compile the Model

• The Adam optimizer and binary cross-entropy loss function train the model.

Train the Model

• The fit method is then used to train the model for 50 epochs with a batch size of 32.

Extract the Bottleneck Representation of The Input Data

• Finally, the code defines a new model, which is used to extract the bottleneck representation of the input data by connecting the input layer to the bottleneck layer and using the predict method to get the bottleneck representation.

These are just examples, and the choice of dimensionality reduction technique and the specific implementation will depend on the specific task and the type of data you are working with.

In summary, to mitigate the curse of dimensionality in geometric deep learning, dimensionality reduction techniques such as PCA and Autoencoder can be used, which can project high-dimensional data onto a lower-dimensional subspace or learn a lower-dimensional representation of the data, making it easier to train deep learning models on the data.

Real-Life Examples of the Curse of Dimensionality

Here are a few examples of real-life scenarios where the curse of dimensionality can be a challenge:

1. Computer Vision:
   In image recognition, the curse of dimensionality can occur when analyzing high-resolution images. Each pixel in an image can be considered a dimension, and an image with high resolution can contain millions of pixels, making it computationally expensive and difficult to analyze.
2. Natural Language Processing:
   In NLP, the curse of dimensionality can occur when analyzing text data with a large vocabulary. Each word in a vocabulary can be considered a dimension, and a large vocabulary can contain thousands of words, making it difficult to analyze the text data effectively.
3. Recommender Systems:
   The curse of dimensionality can occur when analyzing large datasets with many users and items in recommendation systems. Each user and item can be considered a dimension, and a large dataset can contain millions of users and items, making it difficult to analyze the relationships between them.
4. Robotics:
   In Robotics, the curse of dimensionality can occur when trying to analyze large datasets from high-dimensional sensor measurements, such as lidar and cameras, which can contain thousands of features per measurement, making it difficult to analyze the data effectively
5. Climate modeling:
   In climate modeling, the curse of dimensionality can occur when analyzing large datasets from high-dimensional atmospheric measurements, such as temperature, humidity, and pressure, which can contain thousands of features per measurement, making it difficult to analyze the data effectively.

Overall, the curse of dimensionality is a common challenge in many fields, such as computer vision, natural language processing, recommender systems, robotics, and climate modeling, where the number of features or dimensions in the datasets can become very large, making it difficult to analyze and process the data effectively.

Contributions of Geometric Deep Learning

Geometric Deep Learning is an emerging field that aims to extend deep learning techniques to non-Euclidean domains such as graphs and manifolds. It has made several key contributions, such as:

• Graph Convolutional Networks (GCNs) for processing data on graphs, which have been applied in many domains.
• Spectral methods for analyzing data on manifolds, which have been applied in various domains such as computer vision, speech processing, and natural language processing.
• Geometry-aware representations, allowing models to learn representations that are aware of the underlying geometry of the data.
• Graph Attention Networks allow for weighting of the importance of information flow between nodes.
• Generative models that can generate new samples on non-Euclidean domains, such as graph variational autoencoders applied to domains like drug discovery and computer-aided design.