C++ Program for Heap Sort

Introduction to Heap Sort C++

Heapsort C++ is one of the comparison-based sorting algorithms. Heap sort is also an improved selection sort. The Binary Heap data structure is the basis for the comparison process used by the heapsort algorithm. A binary heap is a complete binary tree following the property that every tree's parent must be greater than (or smaller than) all its children (heap property).

As the name suggests, heapsort, the unsorted array, is initially used to generate a heap of data elements, after which the largest item is found and placed at the end of the partially sorted array. It reconstructs the heap once more, looks for the largest record piece, and inserts it into the following open slot from the end of the partially sorted arrangement of records. This process is repeated until there are no more objects in the heap.

Heap sort differs from selection sort in that it arranges the unsorted region in a heap data structure rather than traversing it linearly, making it easier to identify the desired element quickly and effectively.

Algorithm

Given below are the steps for the heapsort C++ algorithm:

• Create a max heap using the supplied data, with the root as the highest element.
• Then, we have to reconstruct the heap by swapping the root element (i.e., the highest element) with the last element of the heap and then remove the last element of the heap from the heap.
• Then, modify the max heap to not go against the maximum heap's properties (Heapify).
• The heap size is decreased by 1 in the step above.
• The heap is then created again using the leftover elements, which is repeated until all elements are sorted.

Illustration

Take a look at the following list of elements. This array has to be sorted using the heap sort method :

Now, let's construct the max-heap of the array which is given above:

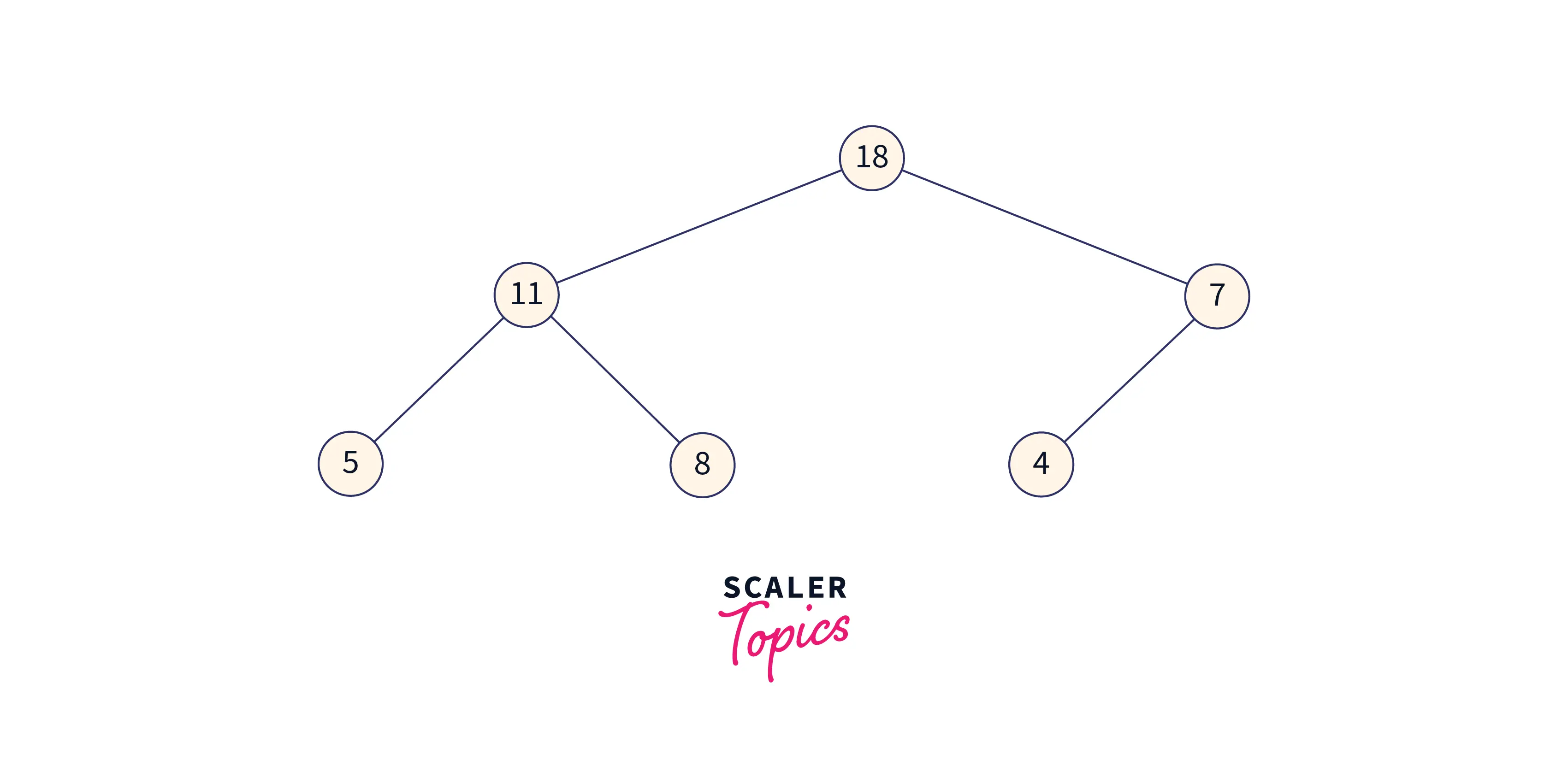
When the heap is finished being built, we represent it as an Array, as seen below :

The first node (root) and the last node are now compared and then swapped. We swap positions so that element 4 is in index 1 of the array and 18 is in the last index of the array.

As seen in the shaded area below, we now remove node 18 from the heap and place it in the sorted array.

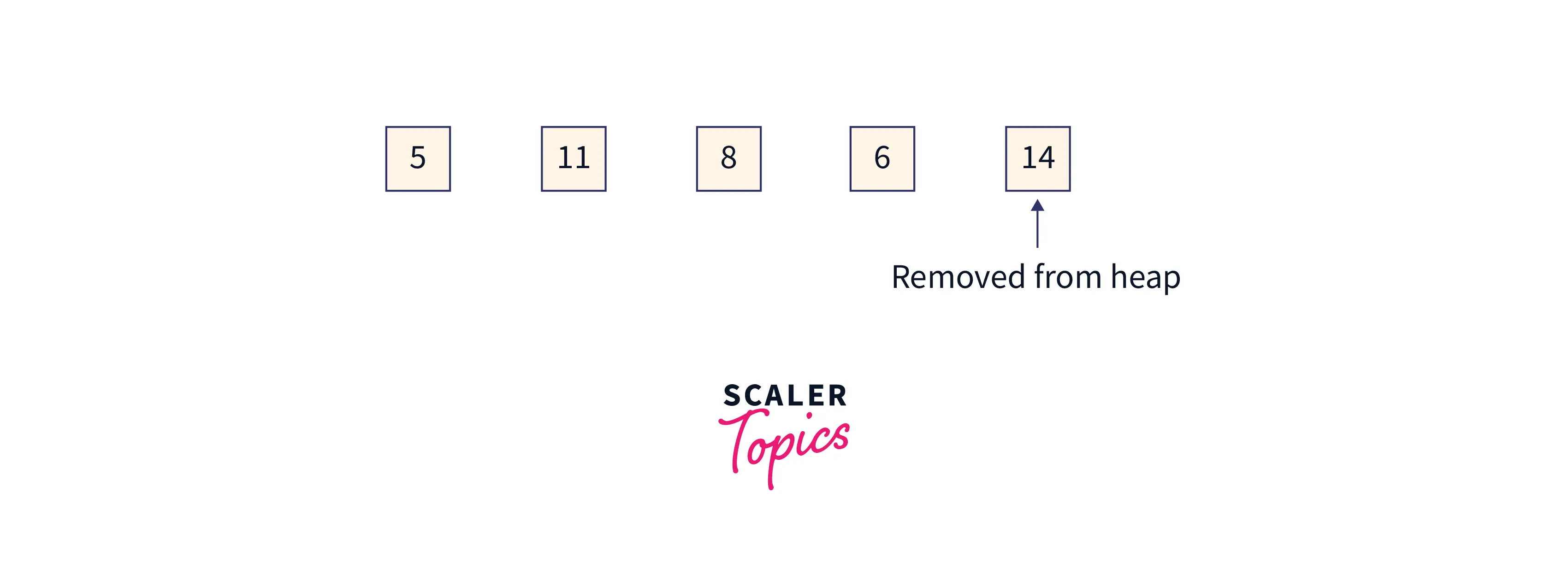
Now we again construct a heap from the remaining element left in the array by heapify, and we observe that the array size is reduced by 1 this time as we have deleted one element(18) from the heap.

Then the modified heap after removing the element will be:

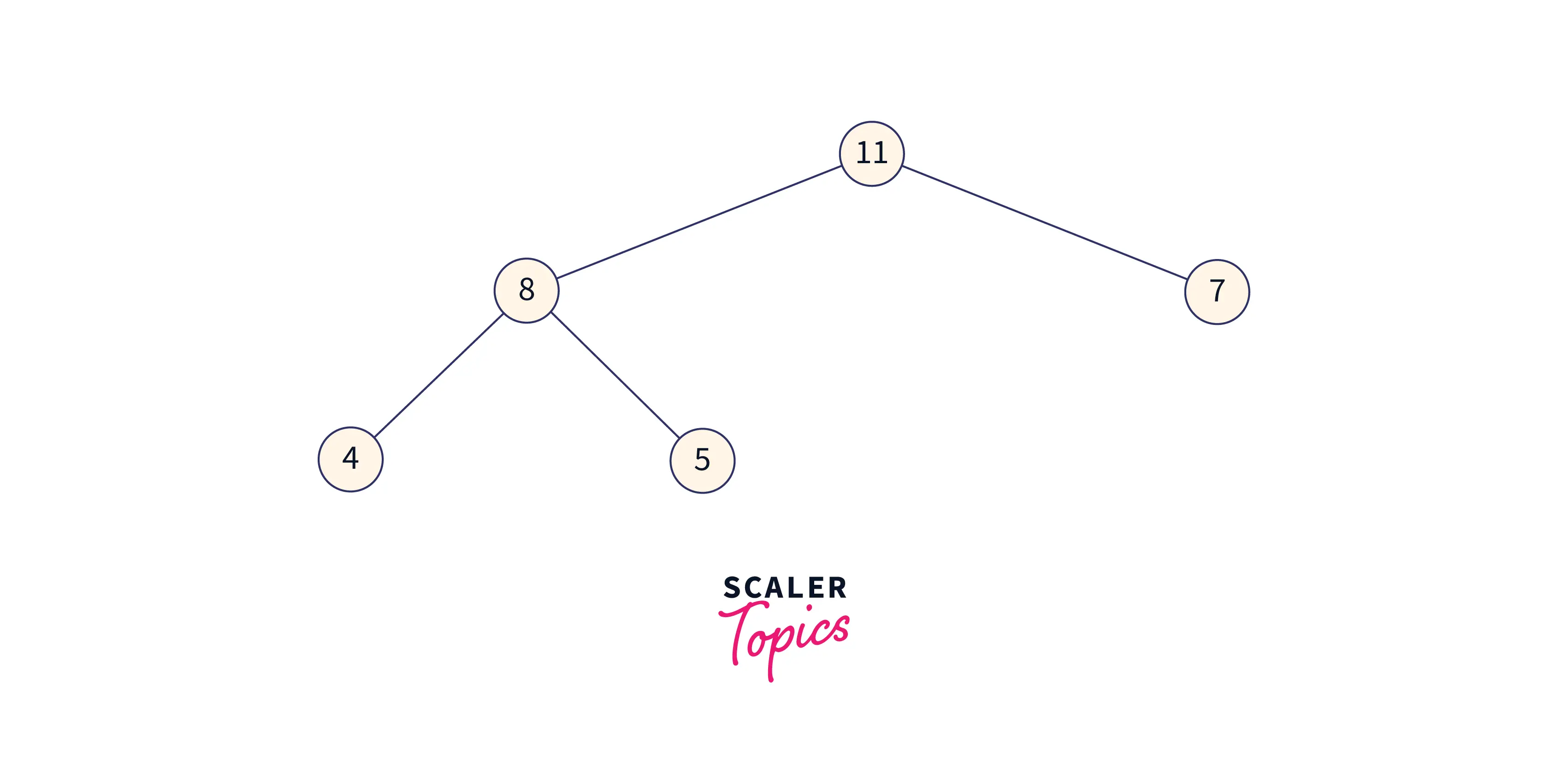
We will repeat the same step of putting the max element of the heap in the sorted array part and then heapify the remaining heap until all array gets sorted.

So, the array sorted due to the heap sort is displayed above.

We have arranged the array in ascending order in the example above. The same procedures must be used with the min-heap if we need to sort the array in descending order.

The heapsort algorithm is the same as selection sort in that it chooses the smallest value and inserts it into an array that has been sorted. However, in terms of performance, heap sort outperforms selection sort. To put it simply, heapsort is a better form of selection sort.

Working of Heap Sort

To sort any list using heap sort in C++, follow the steps given below:

• First, we convert the list given into a heap.
• Now, the given heap is converted into max-heap.
• Now, the heap is converted into max-heap, then the largest element in the list is stored in the root of the heap, and further, it is replaced with the last element of the heap.
• This node is deleted, and the heap size is reduced by 1 every time.
• These steps are followed until we get a sorted list.

How to Convert a Given List into Heap?

If an element in the list has an index of i, then the element at index 2i+1 will be its left child, and the one at index 2i+2 will be its right child. Additionally, if we want to identify the parent of any element, we can do so by determining the lower bound, shown by (i-1)/2.

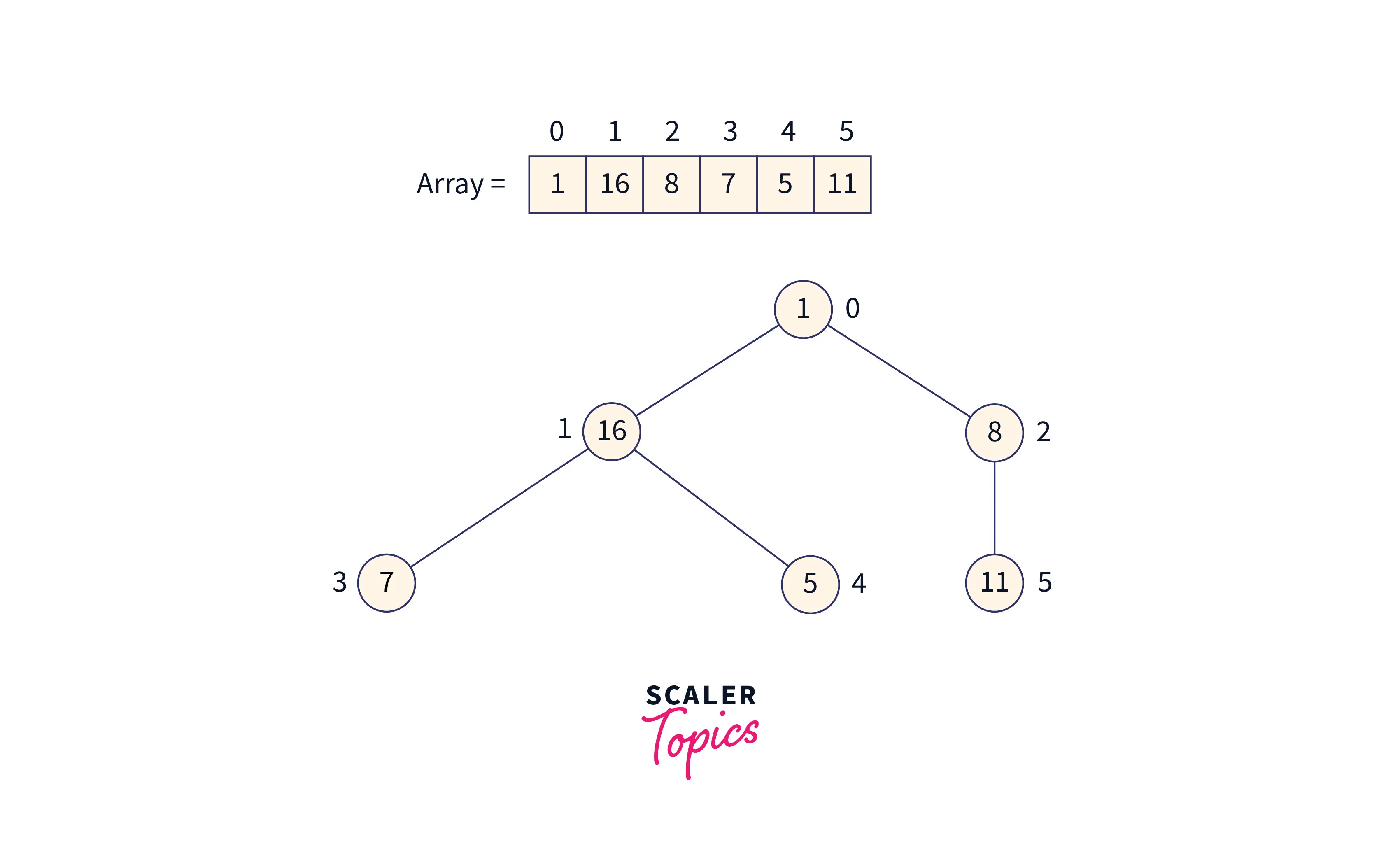
Let's check how the heap is created from the list:

For index= 0, element = 1

Left child of 1: =element at (2* 0 + 1) index =element at 1 index =16

Right child of 1: =element at (2* 0 +2) index =element at 2 index =8

Similarly, we can perform for other elements also.

Now let's see if the above formula for parents also holds:

For index = 2, element = 8 =(i-1)/2 =(2-1)/2 =1/2 =0.5 ~0 =1

Example of Heap Sort C++

Heap sort in C++ uses the binary heap notion, built using a full binary tree with the root node larger than all its children.

Consider an array of elements :

Array = [6,19,5,14,11,8]

Let's proceed using the algorithm. It instructs to build the largest possible heap while choosing the highest element as the root.

First Iteration

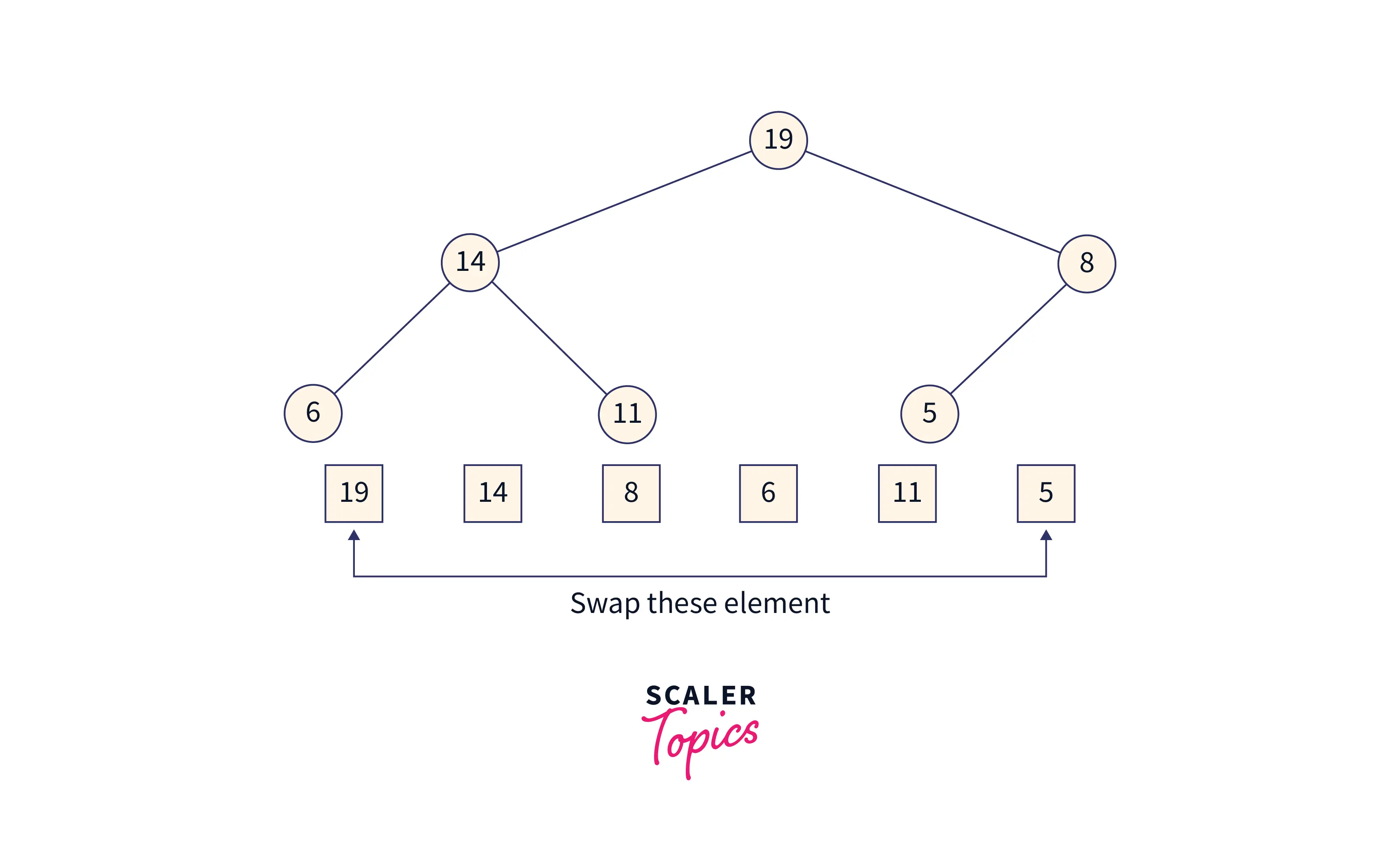
The above figure shows the max-heap of the array.

Now the partially sorted array after swapping the element will look like this:

Array = [5,14,8,6,11,19], index 0 to 4 is the remaining heap, and index 5 to 5 is the sorted array.

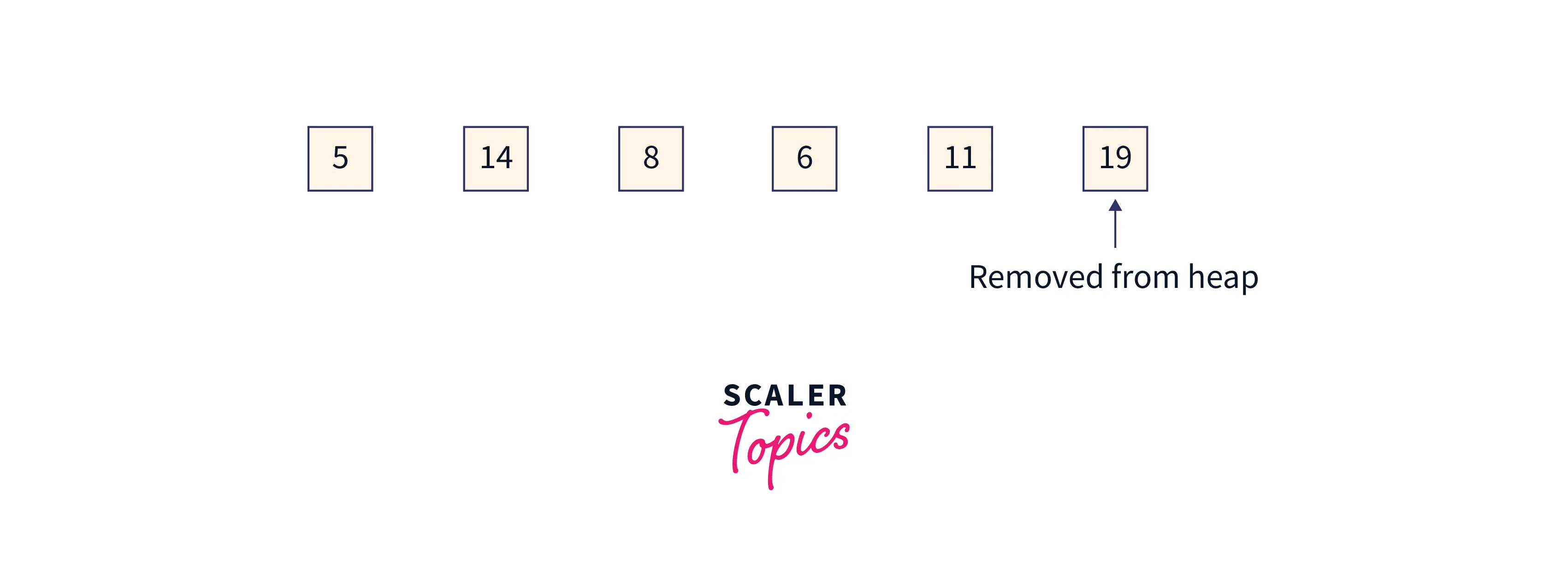
The heap size will now shrink by 1. Now it will be 6-1 = 5.

Second Iteration

The heap now appears after performing the heapify operation over the remaining heap as follows:

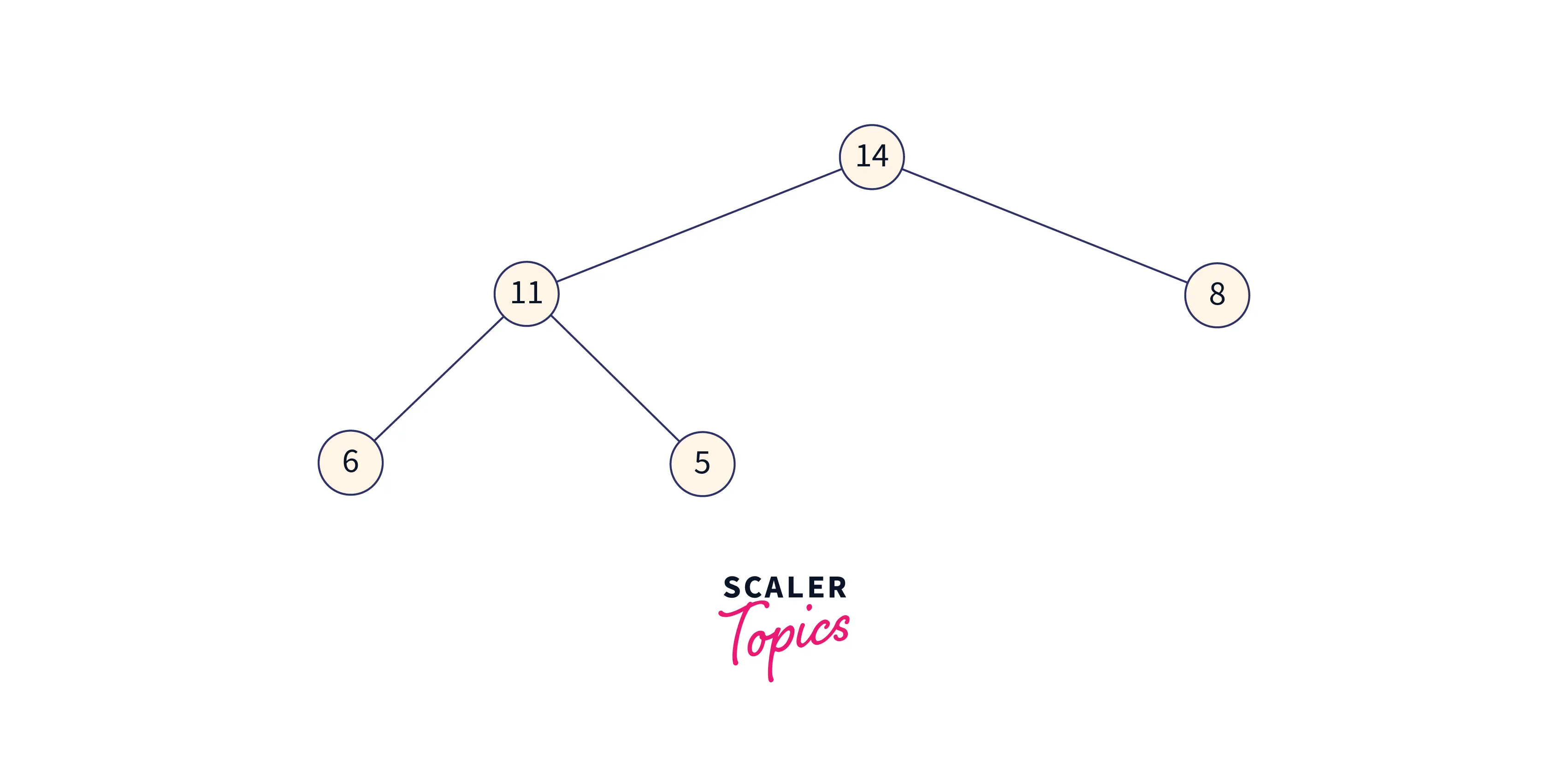
Now the array formed by max-heap will look like this:

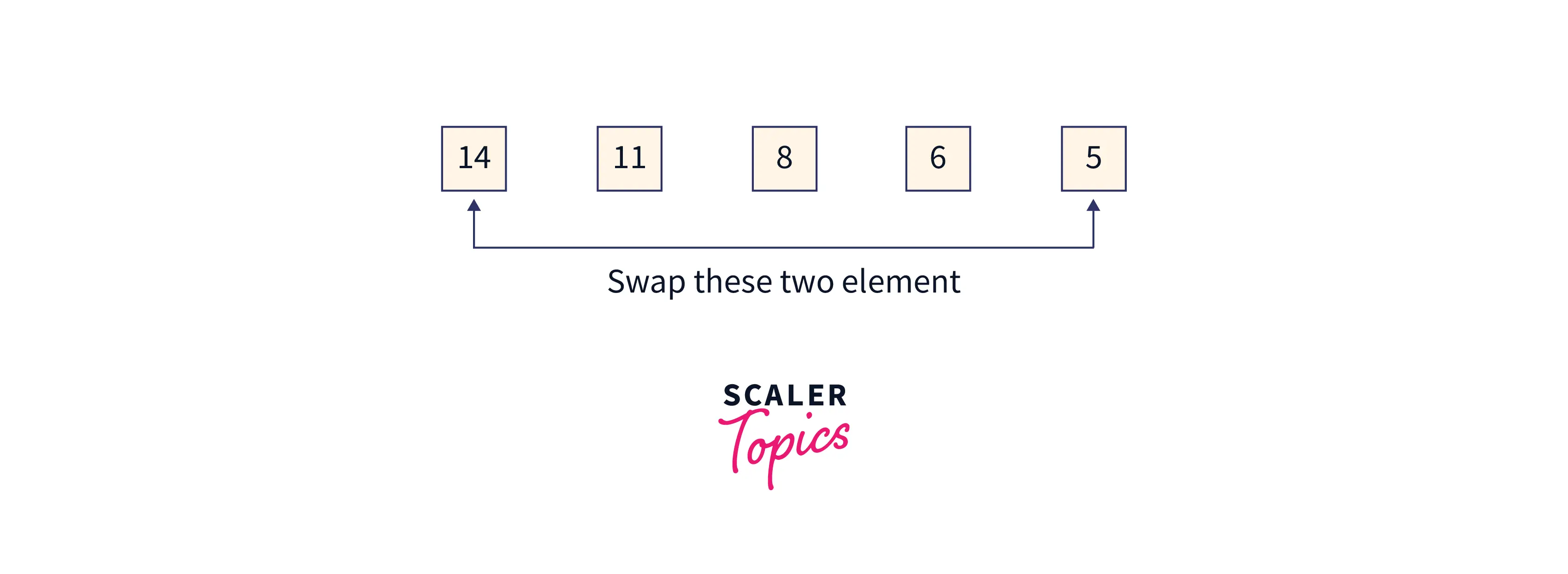
Now the partially sorted array will look like this:

Array = [5,11,8,6,14,19], index 0 to 3 is the remaining heap, and index 4 to 5 is a sorted array.

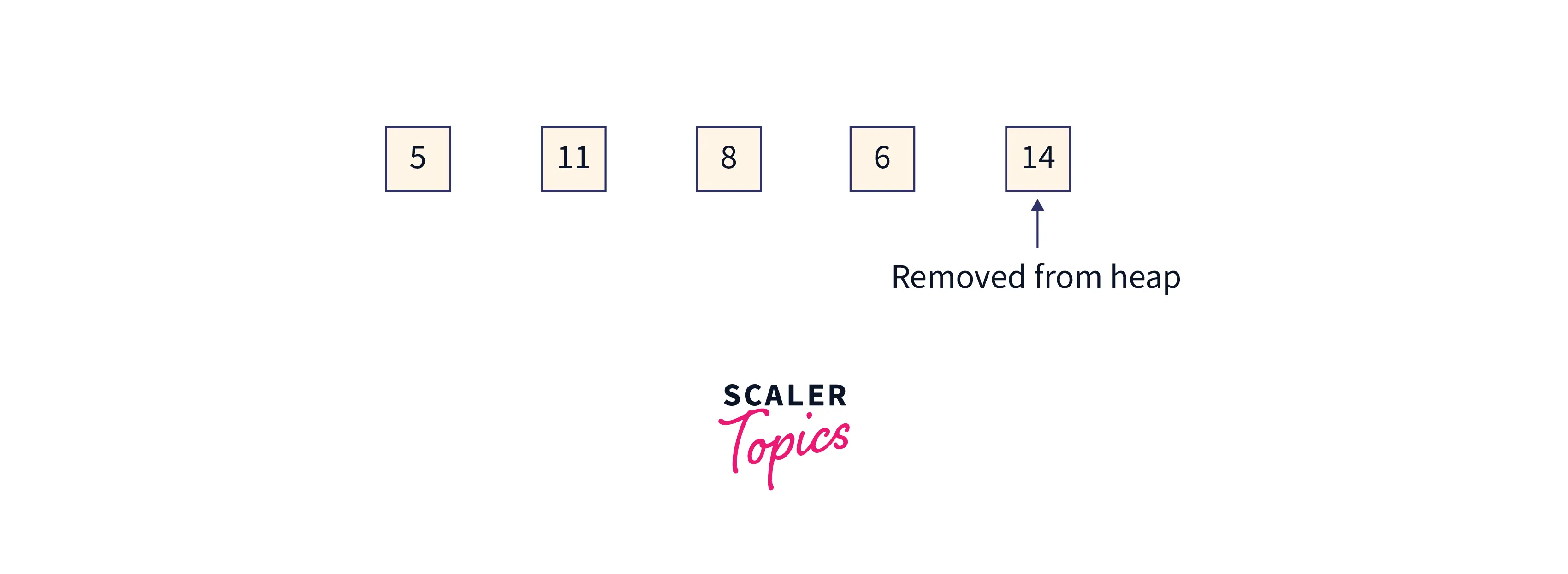
The heap size will now shrink by 1. Now it will be 5-1 = 4.

Third Iteration

The heap now appears after performing the heapify operation over the remaining heap as follows:

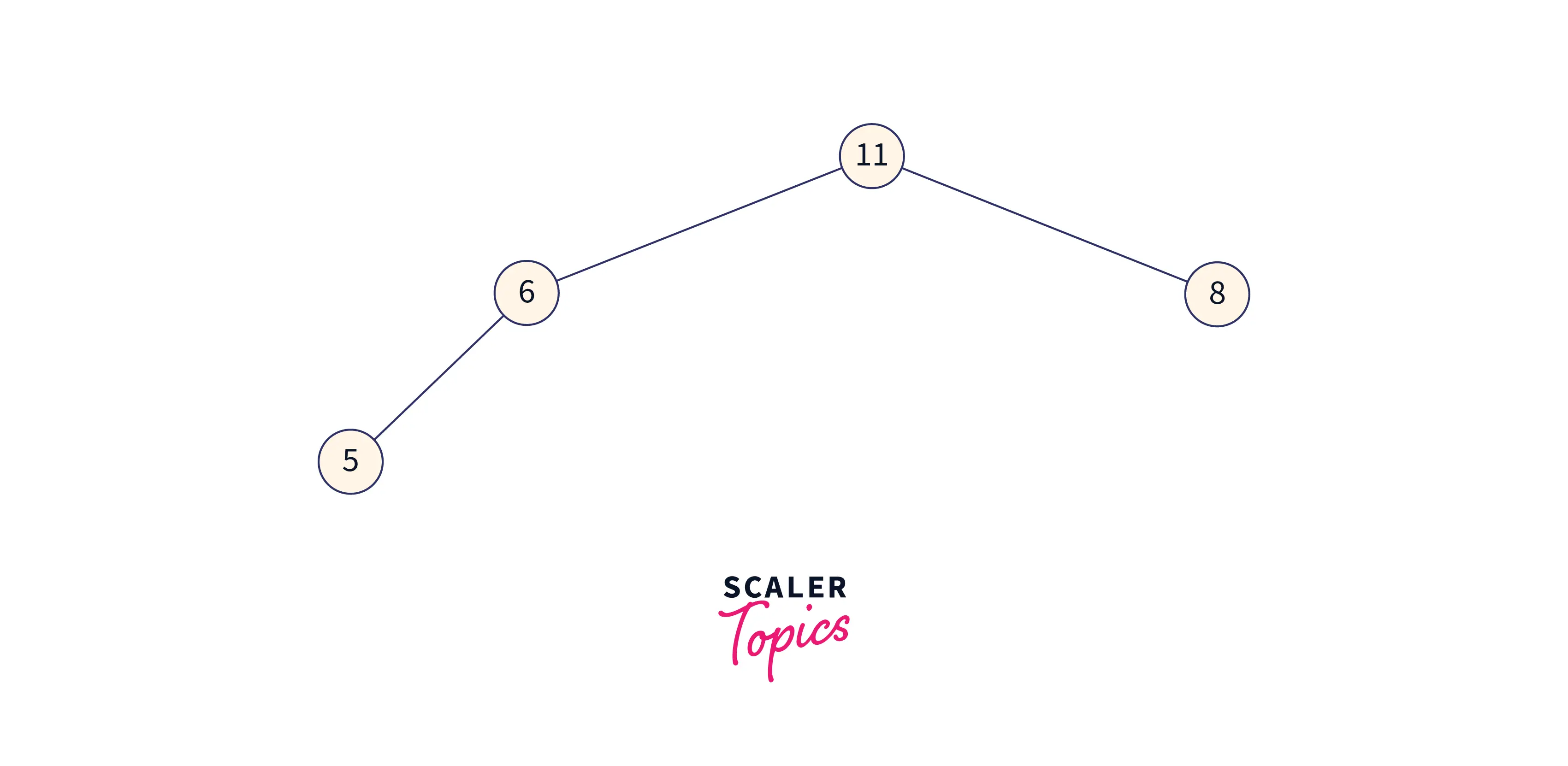
Now the array formed by max-heap will look like this:

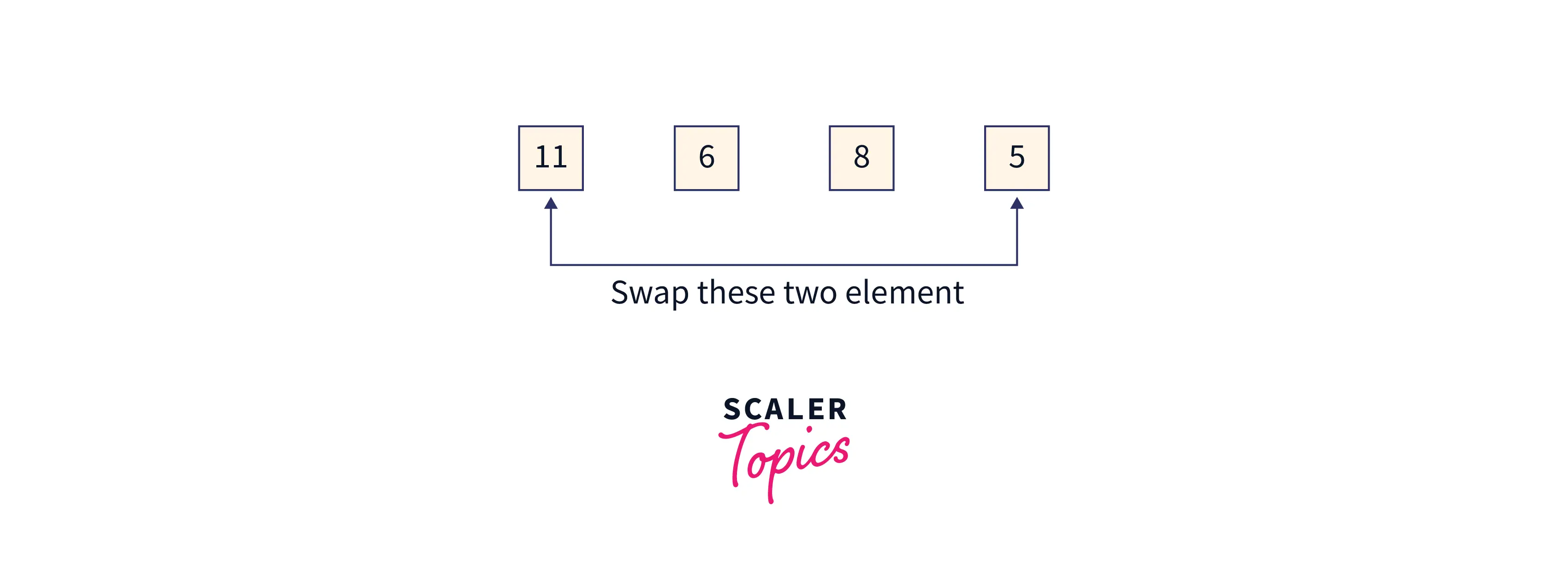
Now the partially sorted array will look like this:

Array = [5,6,8,11,14,19], index 0 to 2 is the remaining heap, and index 3 to 5 is the sorted array.

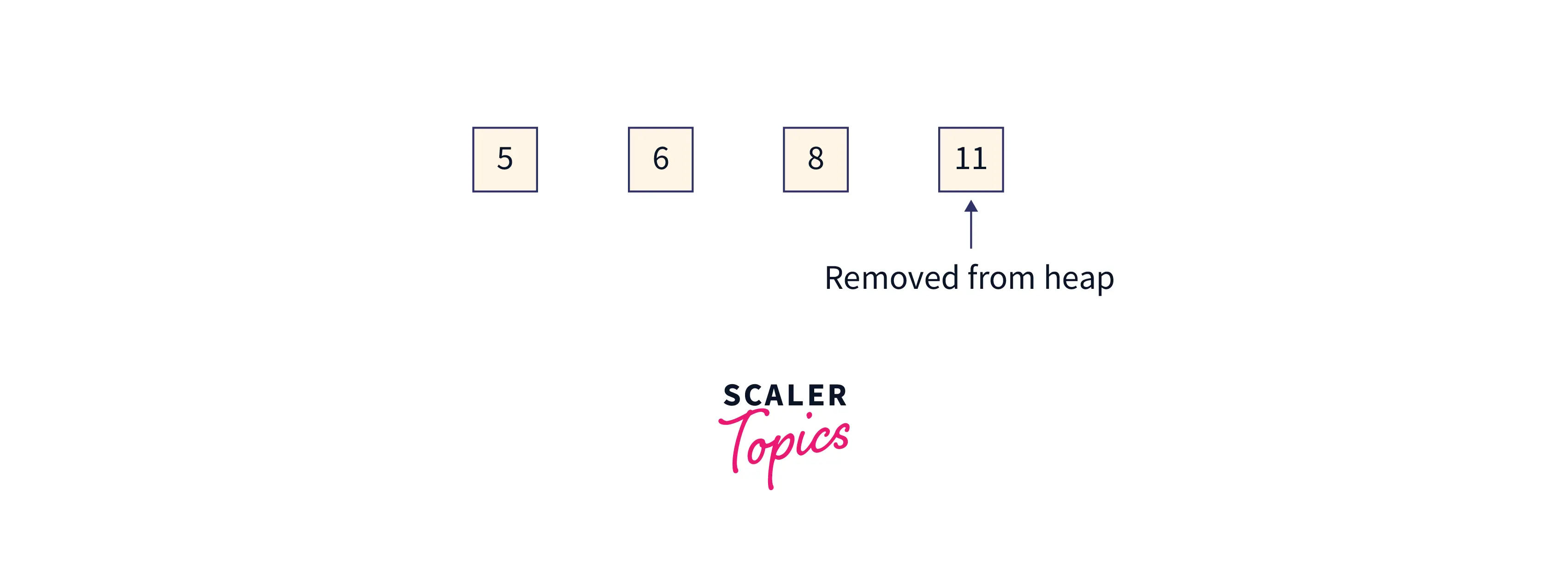
The heap size will now shrink by 1. Now it will be 4-1 = 3.

Fourth Iteration

The heap now appears after performing the heapify operation over the remaining heap as follows:

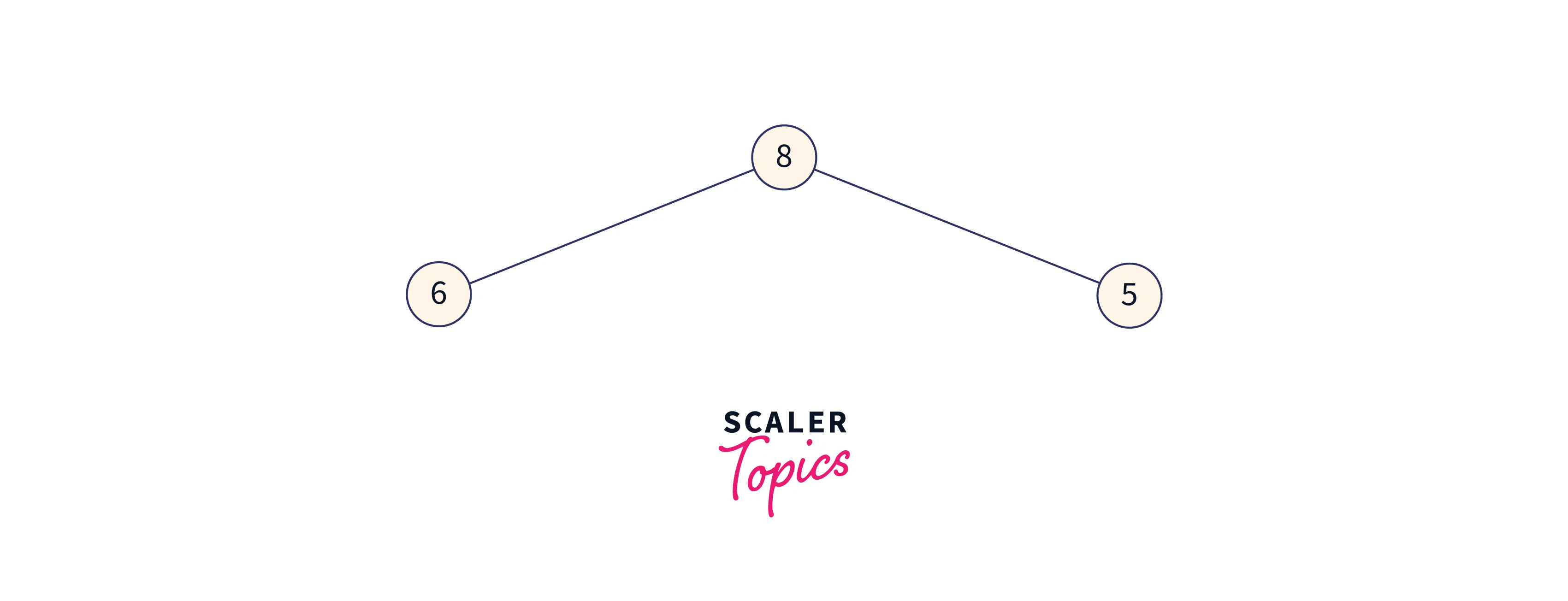
Now the array formed by max-heap will look like this:

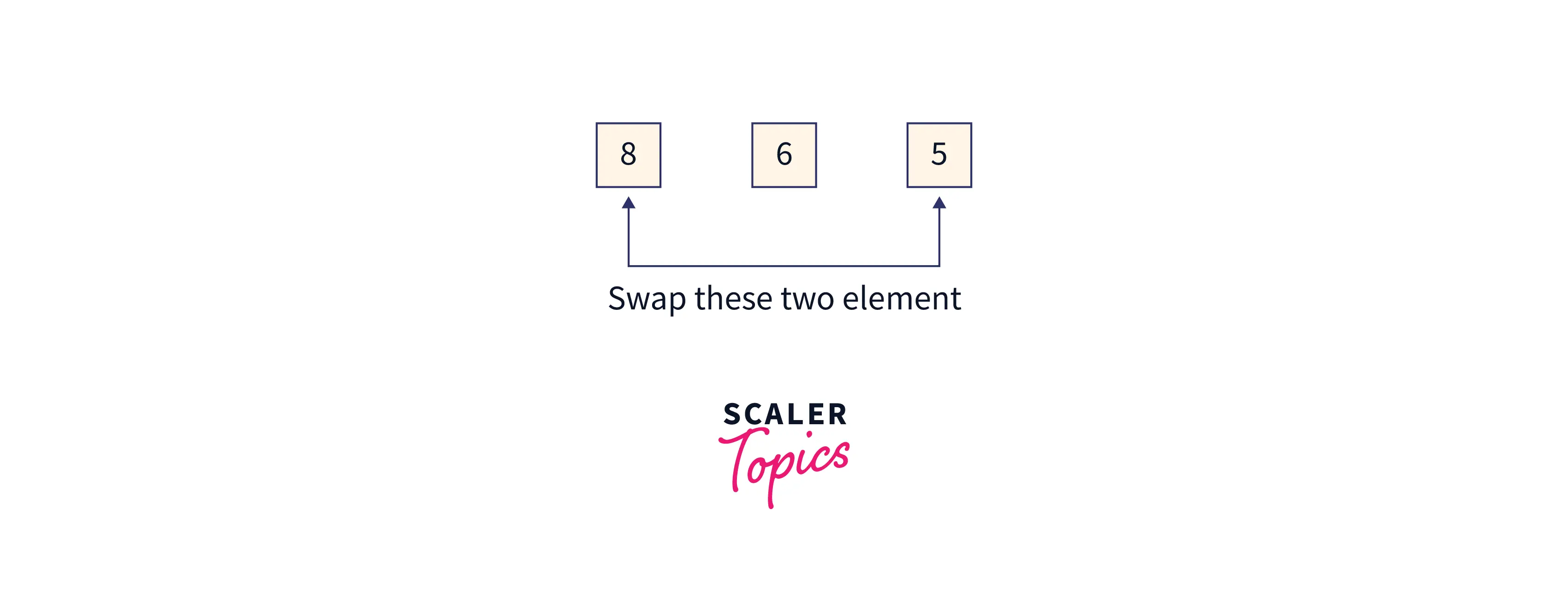
Now the sorted array will look like this:

Array = [5,6,8,11,14,19], index 0 to 1 is the remaining heap, and index 2 to 5 is the sorted array.

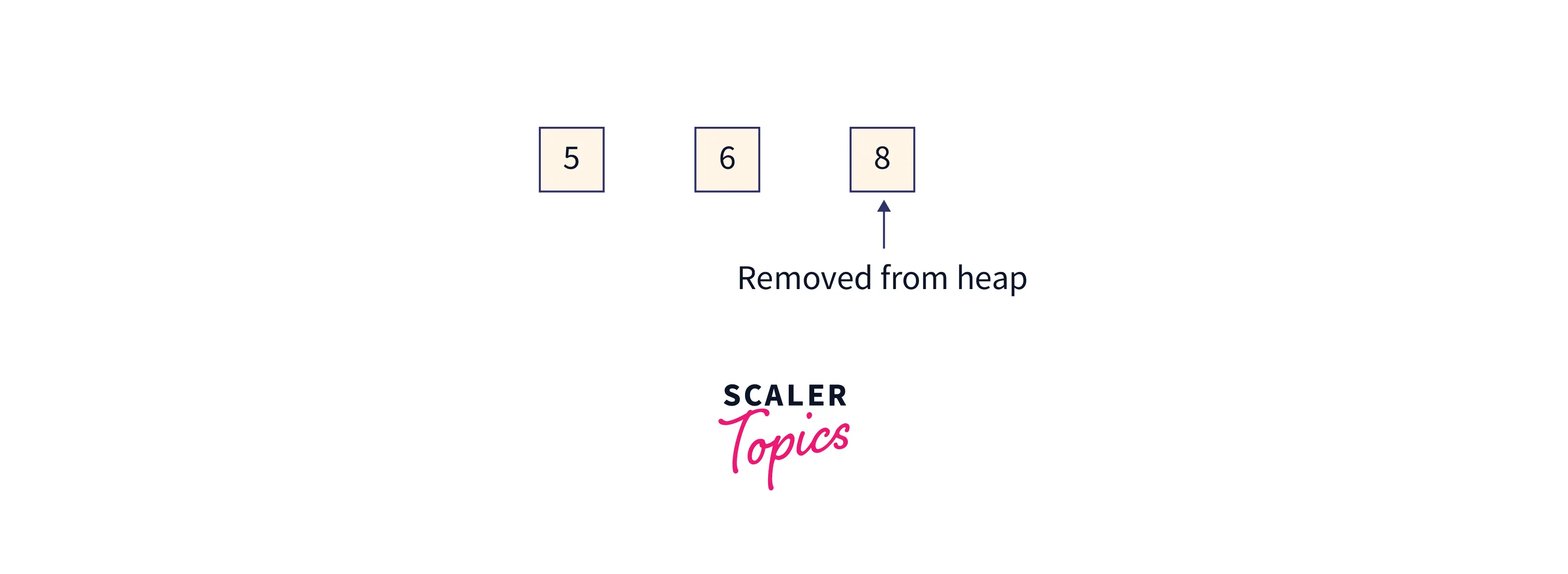
The heap size will now shrink by 1. Now it will be 3-1 = 2.

Fifth Iteration

The heap now appears after performing the heapify operation over the remaining heap as follows:

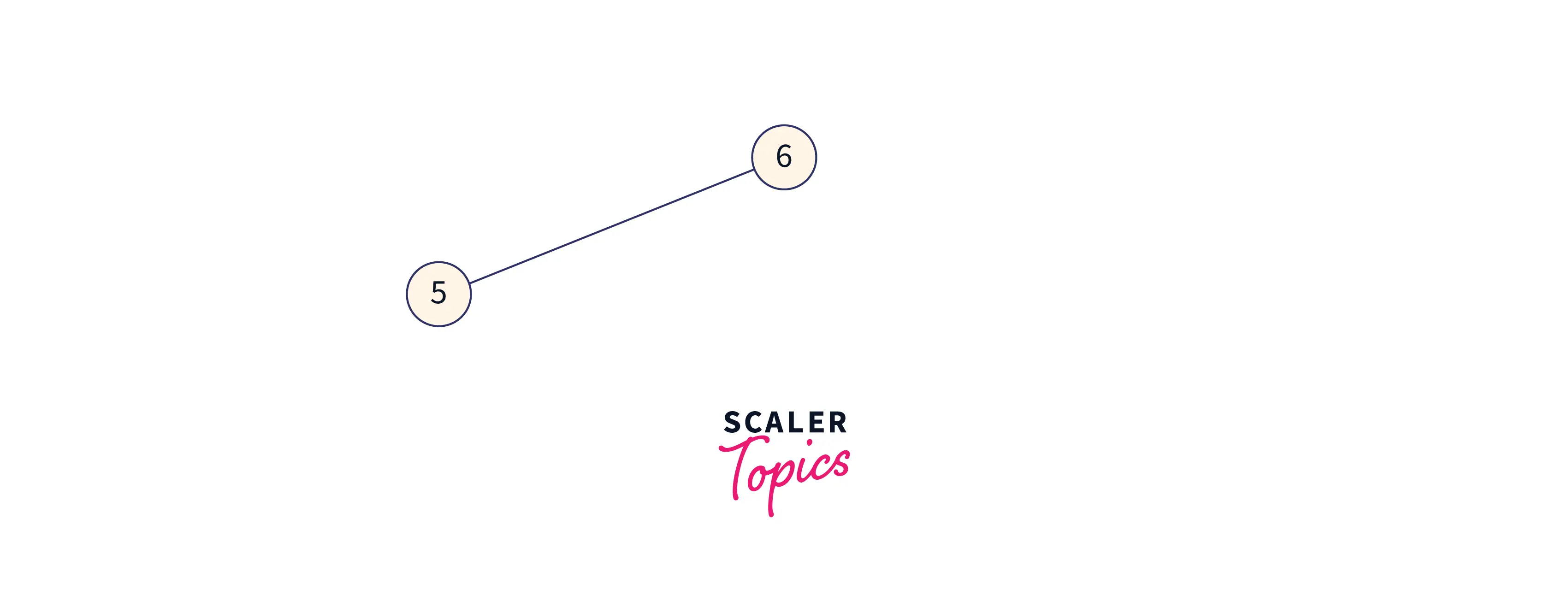
Now the array formed by max-heap will look like this:

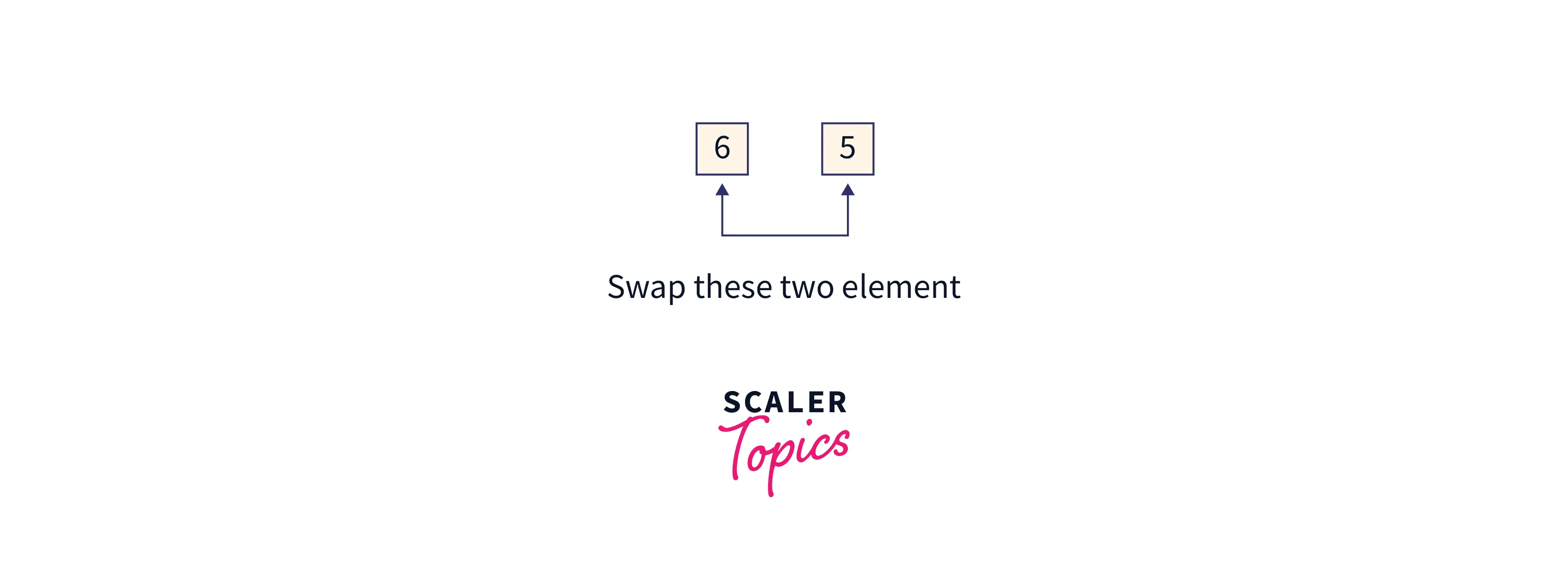
Now the partially sorted array will look like this:

Array = [5,6,8,11,14,19], index 0 to 0 is the remaining heap, and index 1 to 5 is the sorted array.

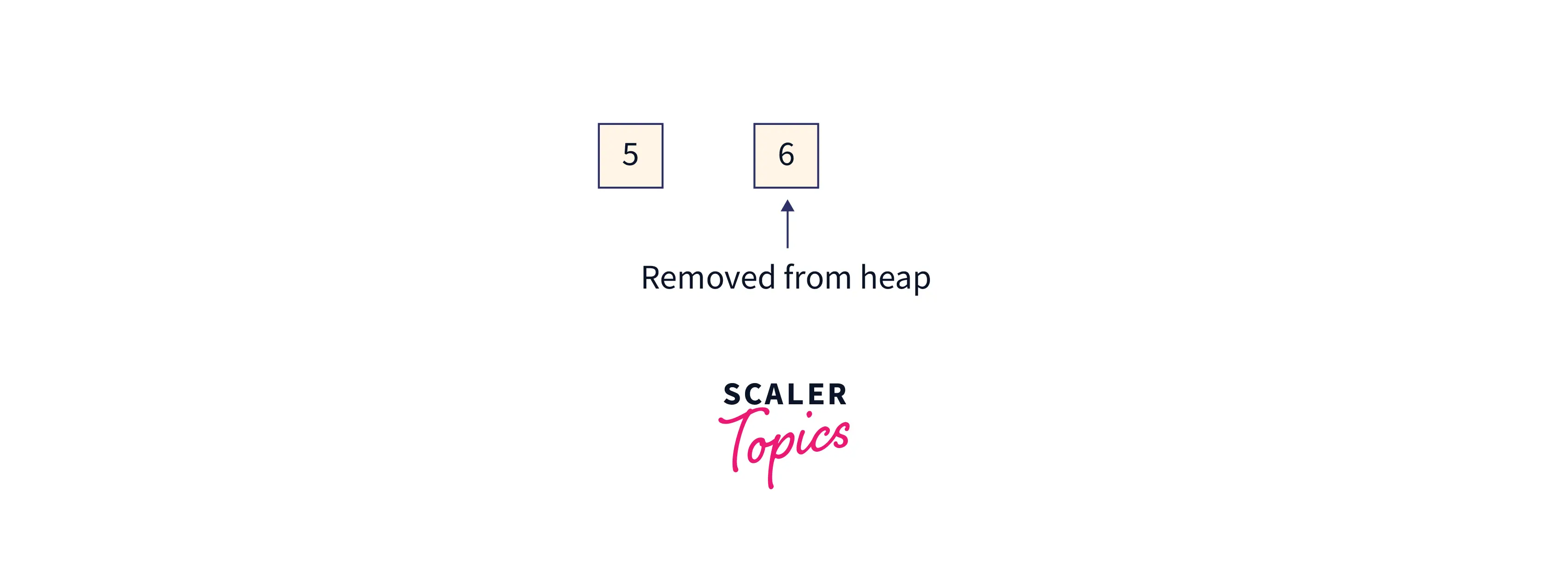
The heap size will now shrink by 1. Now it will be 2-1 = 1.

Last Iteration

The heap now appears after performing the heapify operation over the remaining heap as follows:

Now the Array has:

5

We followed the technique exactly up until the heap size reached 1. So now that the array has been sorted:

Array = [5,6,8,11,14,19]

As a result, the max-heap's sorted array is arranged in ascending order. Follow the methods above with a min-heap if we require the array to be sorted in descending order.

Program for Heap Sort with Implementation

Implementation of heap sort in C++:

Example

Output

Explanation

• The function heapify() takes 3 arguments arr, n, i i.e., array, size of the heap, and i is the array index. This function is to build the max-heap repeatedly.
• Now, we call the function heapSort(). It extracts an element from the heap and then swaps the current, i.e., the largest element, to the last element of the heap.
• Then we reduce the size of the heap by 1 and then again call the heapify function on the shrunk heap.
• Then, the Print() function is used to print the elements of the array.
• At last the driver function main() takes an array and calls the heapsort() function before and after the sorting as shown above.

Program to Sort an Array of 10 Elements Using Heap Sort Algorithm

Example

The heap Sort algorithm to sort an array is :

Output:

Explanation

• The function heapify() takes 3 arguments arr, n, i, i.e., array, size of the heap, and i is the index of the array. This function is to build the max-heap repeatedly.
• Now we call the function heapSort(), which extracts elements from the heap and then swaps the current, i.e., the largest element with the last element of the heap.
• Then we reduce the heap size by 1 and then again call the heapify function on the shrunk heap and repeat this process until the heap size is reduced to 1.
• Then, the print_Array() function is used to print the elements of the array.
• At last, the driver function main() which takes an array and call the heapsort() function before and after the sorting as shown above.

Complexity of Heap Sort

1. Time Complexity:

• Best case : O(nlogn)
• Average case : O(nlogn)
• Worst case : O(nlogn)

Let us understand why heap sort has O(nlogn) complexity in all the cases. A full binary tree with n items has a log nheight.

As we have already witnessed, when heapifying an element whose subtrees are already max-heaps, the element must be lowered, and its left and right children compared to it until both children are smaller. In the worst case, a factor of log(n) comparisons and swaps will be needed to descend one element from the root to the leaf node.

We do it for n/2 elements in the build max heap stage, making the worst-case complexity of the build heap step $n/2*logn ~ nlogn$.

2. Space Complexity: Heap sort has a space complexity of O(1). This is due to the fixed amount of variables we have used, which means that aside from the loop variables and additional variables like temp, n, index, and biggest, we do not require any additional memory space. It indicates that an array of about 1000 elements can be sorted even without using a second variable.

Stable : No

Application of Heap Sort

• Because Heap Sort's running time has an upper bound of O(n log n) and its auxiliary storage has an upper bound of constant O(1), it is used by embedded systems and security-conscious systems like the Linux Kernel.
•  To efficiently extract the smallest (or largest) item from a list of things without incurring the cost of maintaining the other items in the sorted order, we can leverage the heap data structure that underlies it—for instance, Priority Queues.

Read More:

• Array in C++.