Inversion Count in an Array

The Inversion count in an array indicates the number of element pairs (i, j) where i < j and A[i] > A[j], serving as a measure of the array's unsortedness. Understanding Inversion count in an Array is essential for analyzing sorting algorithms' efficiency and optimizing them, making count inversion a key concept in algorithm design and data analysis.

Problem Statement

Given an array $A$ containing $N$ integers. The problem is to find the number of inversions in the array $A$. An inversion is defined as a pair $(i, j)$ such that $i < j$ and $A[i] > A[j]$. We need to find the inversion count for the input array $A$. Note that the array $A$ can contain duplicate elements.

Example 1

$N = 5$ $A = \{1, 5, 3, 2, 3\}$ Output

Example Explanation 1

In this example, the inversion pairs are: $(2, 3)$ as $2 < 3$ and $A[2] > A[3]$. $(2, 4)$ as $2 < 4$ and $A[2] > A[4]$. $(2, 5)$ as $2 < 5$ and $A[2] > A[5]$. $(3, 4)$ as $3 < 4$ and $A[3] > A[4]$. Overall, we have $4$ inversion pairs.

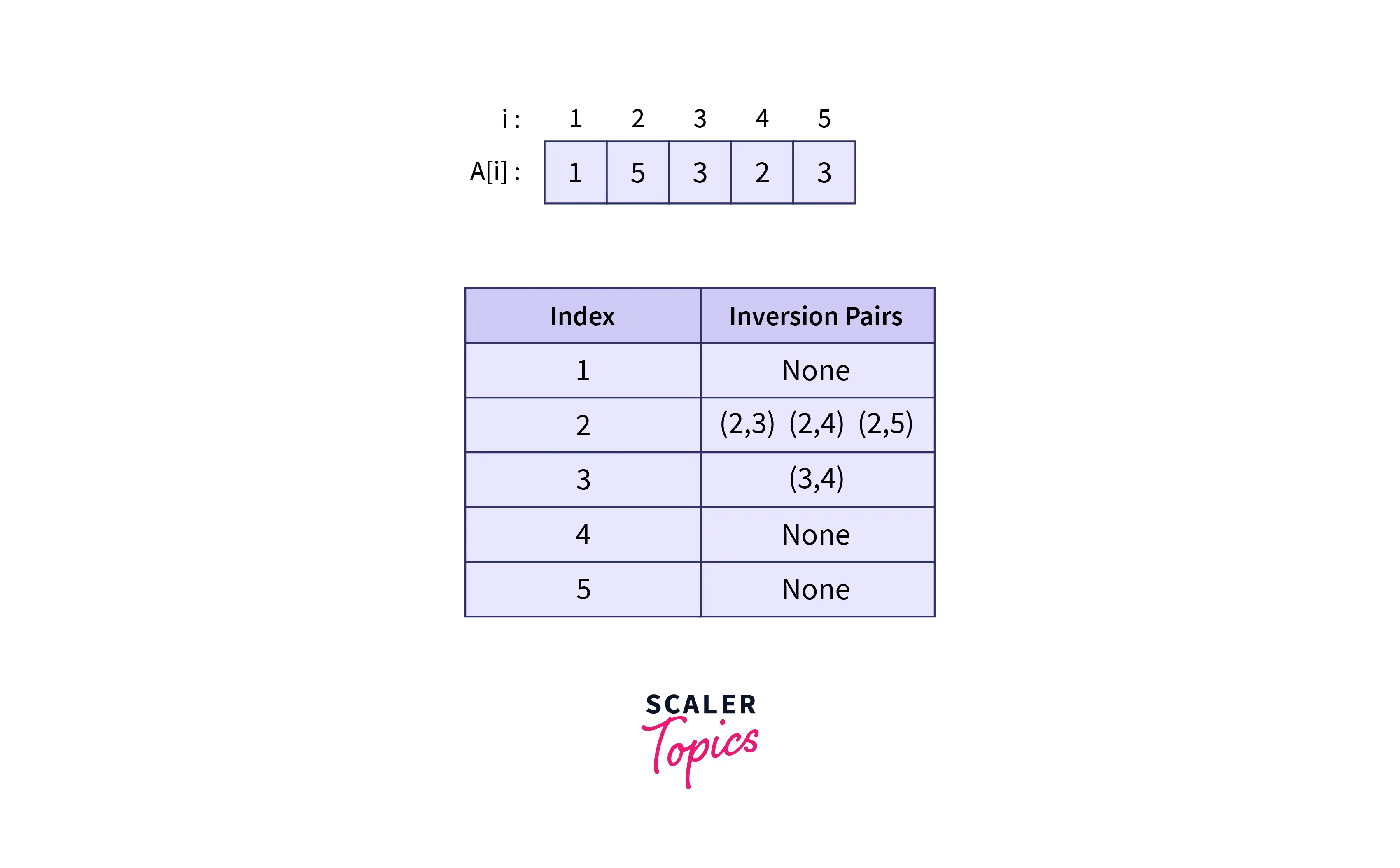
Example 2

$N = 4$ $A = \{109, 56, 20, 1\}$ Output 6

Example Explanation 2

In this example, we have the following inversion pairs: $(1, 2) (1, 3) (1, 4)$ $(2, 3) (2, 3)$ $(3, 4)$

Example 3

$N = 5$ $A = \{1, 2, 3, 4, 5\}$ Output 0

Example Explanation 3

In this example, there are no inversion pairs as for all $i < j, A[i] <= A[j]$.

Constraints

$1 <= N <= 10^6$
$-10^9 <= A[i] <= 10^9$

Approach 1: Brute-Force Solution

A simple approach to find the inversion count for the array is to consider every possible pair of indices $(i, j)$ and check whether this pair forms an inversion. We will maintain a variable to count the total number of inversion pairs. If this pair $(i, j)$ satisfies the conditions that $(i < j)$ and $(A[i] > A[j])$ then increase the counter by 1.

Algorithm

Step 1: Iterate $i$ from $1$ to $N-1$ Step 2: Iterate $j$ from $i + 1$ to $N$: Step 3: If $A[i] > A[j]$: Add $1$ to the answer.

We iterate the variable $i$ from $1$ to $N-1$ and the variable $j$ iterates from $i + 1$ to $N$. This guarantees that the condition $(i < j)$ is true. Now, if $A[i] > A[j]$, we can guarantee that $(i, j)$ forms an inversion pair.

Example

$N = 4$ $A = \{5, 3, 2, 4\}$ $inversions = 0$

For $i = 0, j = 1 \Rightarrow A[i] > A[j] \Rightarrow inversions ++$

For $i = 0, j = 2 \Rightarrow A[i] > A[j] \Rightarrow inversions ++$

For $i = 0, j = 3 \Rightarrow A[i] > A[j] \Rightarrow inversions ++$

For $i = 1, j = 2 \Rightarrow A[i] > A[j] \Rightarrow inversions ++$

For $i = 1, j = 2 \Rightarrow A[i] < A[j]$

For $i = 2, j = 2 \Rightarrow A[i] < A[j]$

Total count of inversion pairs = $4$

Implementation in C++

Implementation in Java

Implementation in Python3

Complexity Analysis

Time Complexity

In the implementation, we are looking at all possible pairs $(i, j)$ and we check the condition whether this pair forms inversion pair or not. The total number of such pairs is $N*(N-1)/2$. Hence the time complexity is $O(N * N)$ Time Complexity: $O(N^2)$

Space Complexity

In this method, we only need a constant number of variables for iteration and to store the answer. Hence the space complexity is $O(1)$. Space Complexity: $O(1)$

Approach 2: Using Merge Sort

We can use a modified merge sort to count inversions in the array $A$.

Merge Sort is a divide and conquer algorithm that divides array $A$ into two parts and then recursively sorts the left and right subparts. The conquer step merges the two sorted halves into a single array and returns the merged array as the final answer. This is done recursively for each sorted halves. Finally, we get the sorted array. We can use the same approach to find the total number of inversions in the array $A$.

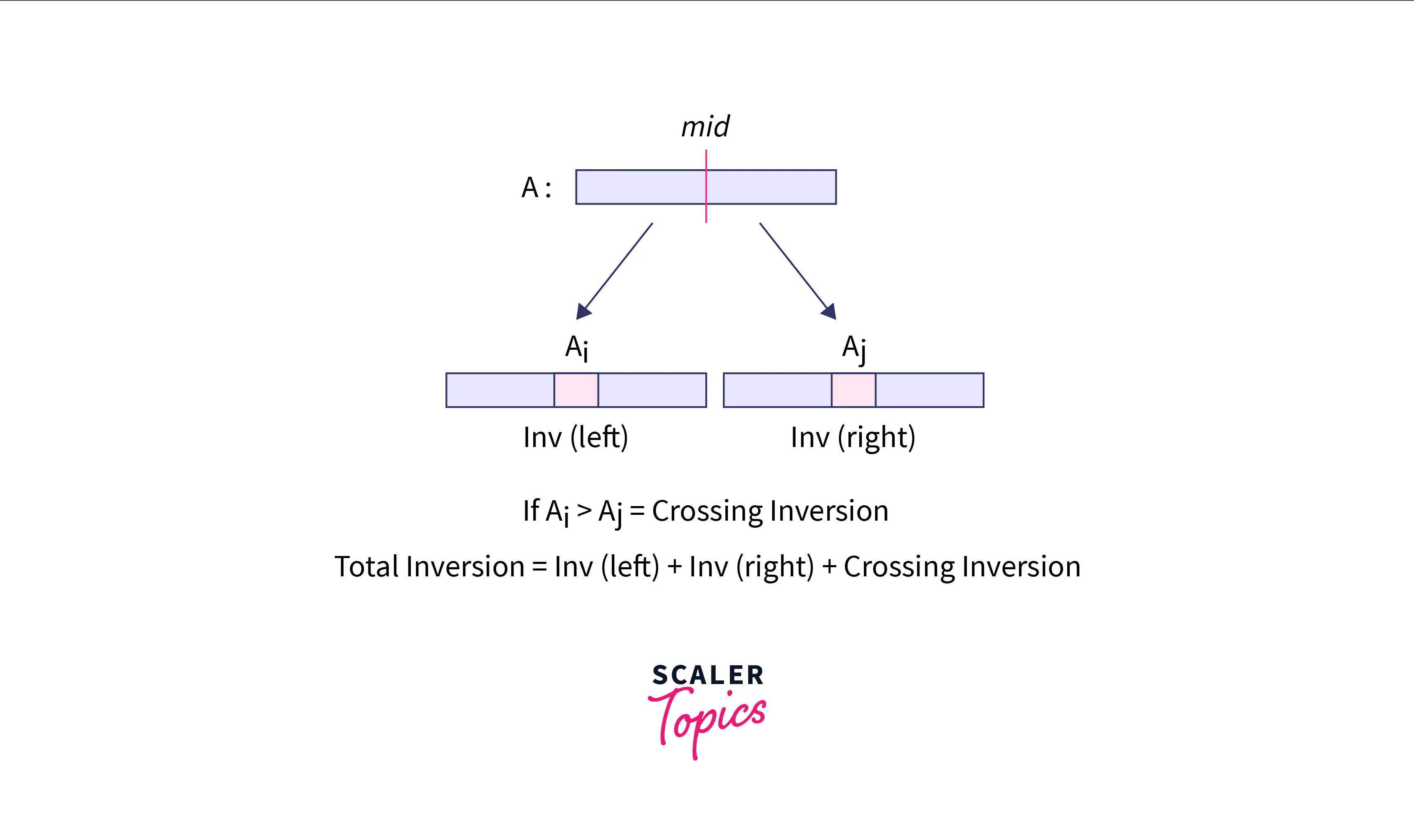
• We will recursively split the array into two halves. The total inversion pairs will be equal to the sum of inversion pairs in the two halves and the number of crossing inversions. Crossing inversion means pairs $(i, j)$ such that $A[i]$ lies in one half and $A[j]$ lies in the other.
• When we have calculated the inversion count in the two halves, we need to add the contribution of crossing inversions. To do this efficiently, we can use a two-pointer approach (explained below) on the sorted halves.
• So we want to calculate the inversion count as well as keep sorting left and right halves. This is similar to the Merge Sort (described above), hence we can modify the same algorithm to calculate the inversions in the array $A$.

We can modify the merge function and find the inversion count using the same approach.

We will divide array $A$ into two equal parts. We will denote $left$ as the left half of array $A$ and $right$ as the right half of array $A$. Try to think about how can we calculate the number of inversion pairs $(i, j)$ recursively such that $A[i]$ lies in the left half of the array and $A[j]$ lies in the right half of the array.

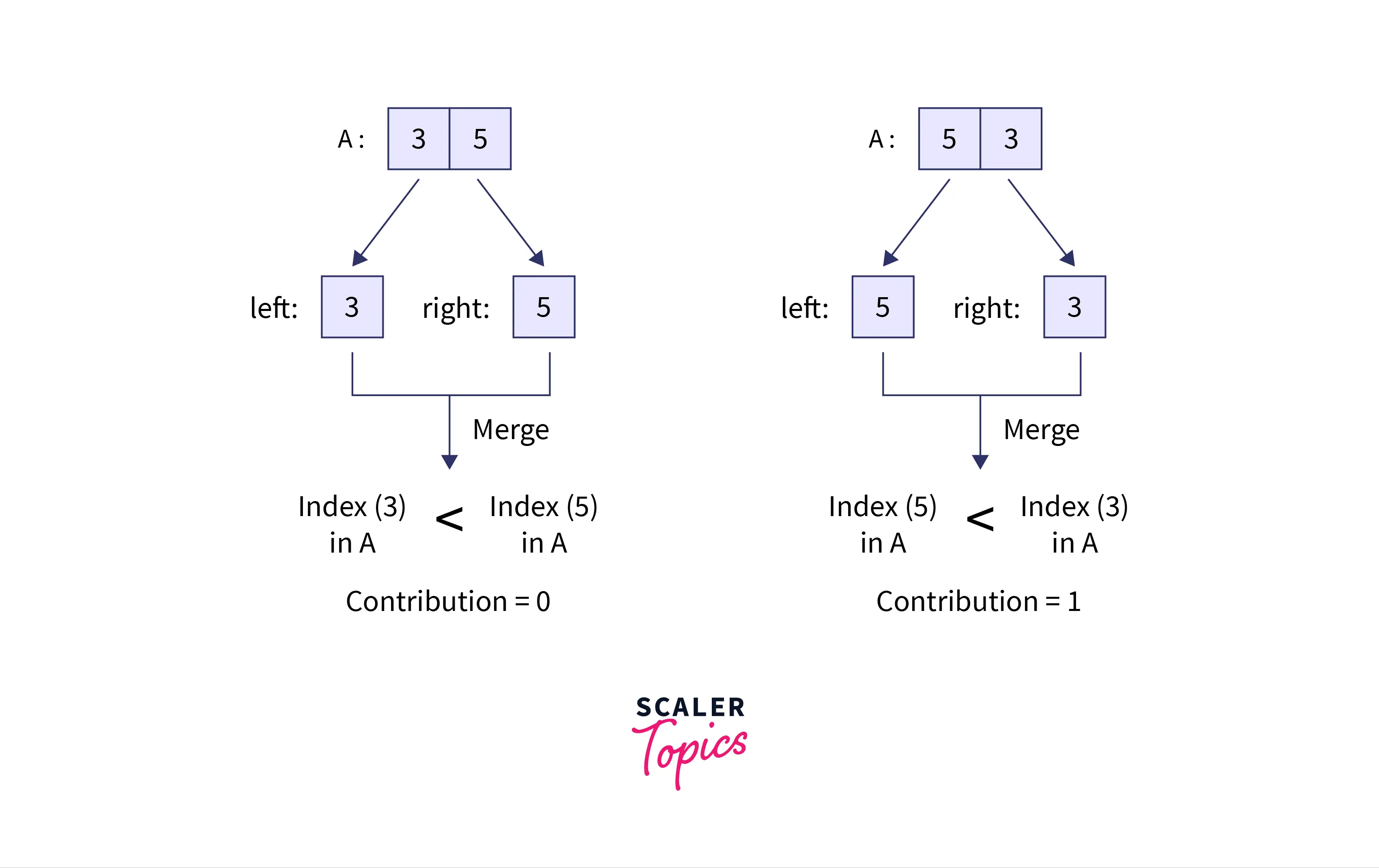
Suppose the left half has only one element and the right half has only one element. In this case, we can say that if $left[0] > right[0]$, then the number of inversion pairs is $1$ else it will be $0$. This is because we know that an element belonging to the array $left$ will have an index less than the element belonging to the array $right$ in the original array $A$. This means the condition that $(i < j)$ is satisfied for these two elements, where $i$ and $j$ denote the index of $left[0]$ and $right[0]$ in array $A$ respectively.

Now consider that the size of the array left and right is $L$, $M$ respectively. We know, Total inversions = Inversion count in the array $left$ + Inversion count in the array $right$ + Count of crossing inversion pairs from $left$ to $right$. Here crossing inversion pairs means the pairs $(i, j)$ such that $A[i]$ lies in the array $left$ and $A[j]$ lies in the array $right$. We are solving this problem recursively, hence we already know the count of inversion pairs in the array $left$ and the count of inversion pairs in the array $right$. We need to count the number of inversion pairs $(i, j)$ such that $A[i]$ lies in the array $left$ and $A[j]$ lies in the array $right$. The sum of inversion pairs in the array $left$, the array $right$, and the crossing inversions is equal to the total inversion pairs. The crossing inversions are calculated while merging the arrays $left$ and $right$.

To do this, we will use the fact that the array $left$ and $right$ are two sorted arrays.

• In the merge function, we use two pointers $p1$ and $p2$ which iterates over the array $left$ and $right$ respectively.
• To merge them, we find the minimum of the two elements $left[p1]$ and $right[p2]$. We append this minimum to the resulting array and increase the pointer accordingly.

While merging, we can calculate the inversion count simultaneously. To do this, observe that:

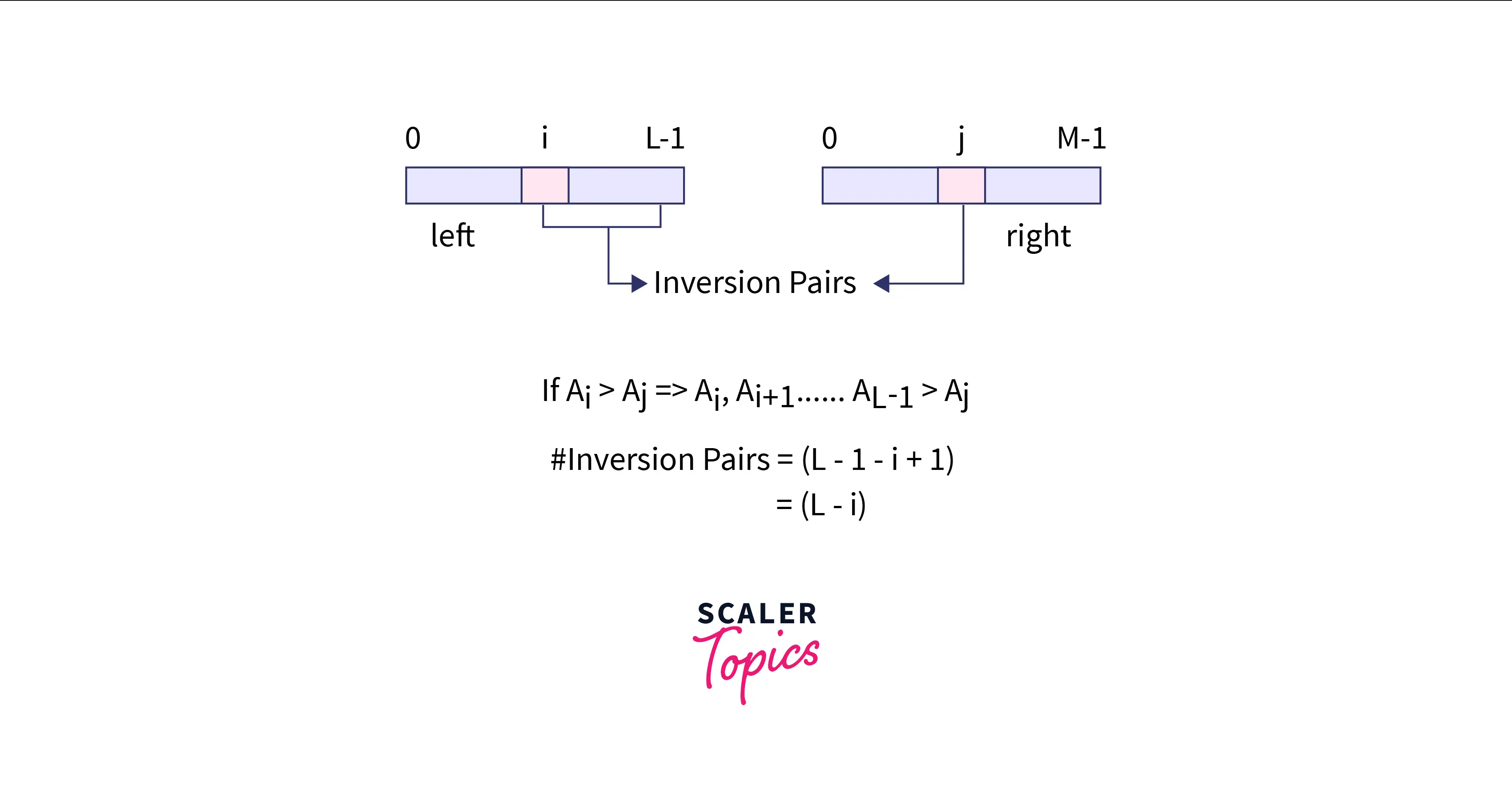
• The elements in the array $left$ will be present before the elements in the array $right$ in the array $A$. This is because, in the divide step, we split the array $A$ into two parts from the middle and the left part ranges from $0$ to $N/2$ and the right part ranges from $N/2 + 1$ to $N - 1$. The $left$ half contains prefix elements of the array $A$, while the right half contains suffix elements of the array $A$.
• So, if there is an element $left[i]$ such that $left[i] > right[j]$, then this pair $(i, j)$ will form an inversion pair. Now since the array $left$ is sorted $left[i+1]$ >= $left[i]$. This means $left[i + 1]$ > $right[j]$ and the pair $(i + 1, j)$ will also form an inversion pair.
• In general, we can say that all the elements in the array $left$ present after the index $i$ will form an inversion pair with $right[j]$ if $left[i] > right[j]$. The contribution of such pairs will be equal to the number of elements present in the range $(i, L-1)$. The number of such elements will be $(L - 1 - i + 1) = (L - i)$. So, we can add $(L - i)$ to the answer. In this way, we can find the number of inversions in the merged array of size $(L + M)$.
• At the end of the merge function, we return the total number of crossing inversion pairs.

Example

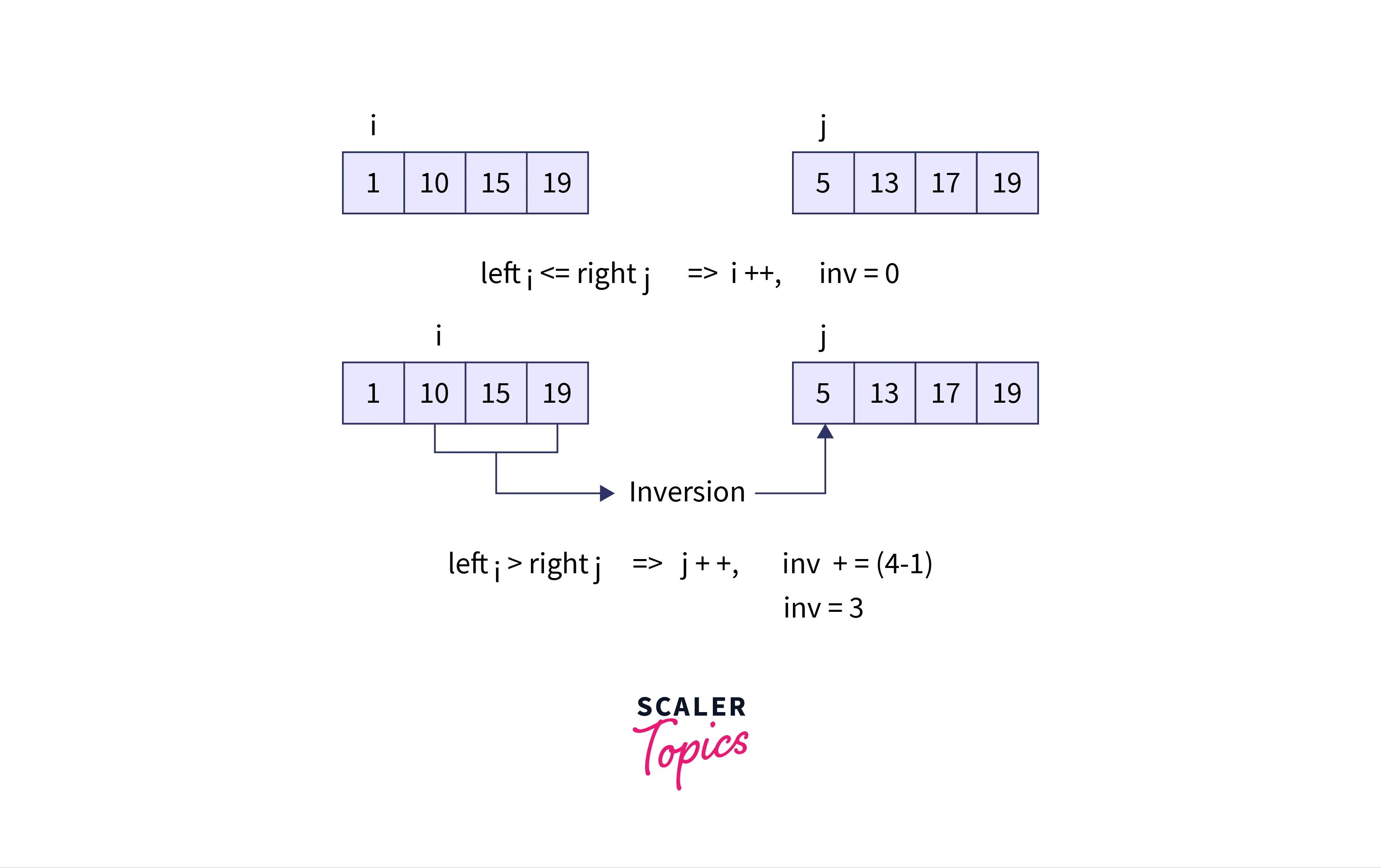
Let us say we want to find the number of crossing inversions and the two halves of the array A are: $Left = \{1, 10, 15, 19\}$, $Right = \{5, 13, 17, 19\}$

Iteration 1:

$Left = \{1, 10, 15, 19\}$, $Right = \{5, 13, 17, 19\}$ Initially $i = 0, j = 0 \Rightarrow Left[i] \leq Right[j]$ $mergedArray = [1]$, $inversion = 0$

Iteration 2:

$i = 1, j = 0 \Rightarrow Left[i] > Right[j]$ $inversion \mathrel{+}= (4 - 1)$ We add the contribution of all elements from $Left[1 … 3]$ with $Right[0]$. $mergedArray = [1, 5], inversion = 3$

Iteration 3:

$i = 1, j = 1 \Rightarrow Left[i] <= Right[j]$ $mergedArray = [1, 5, 10], inversion = 3$

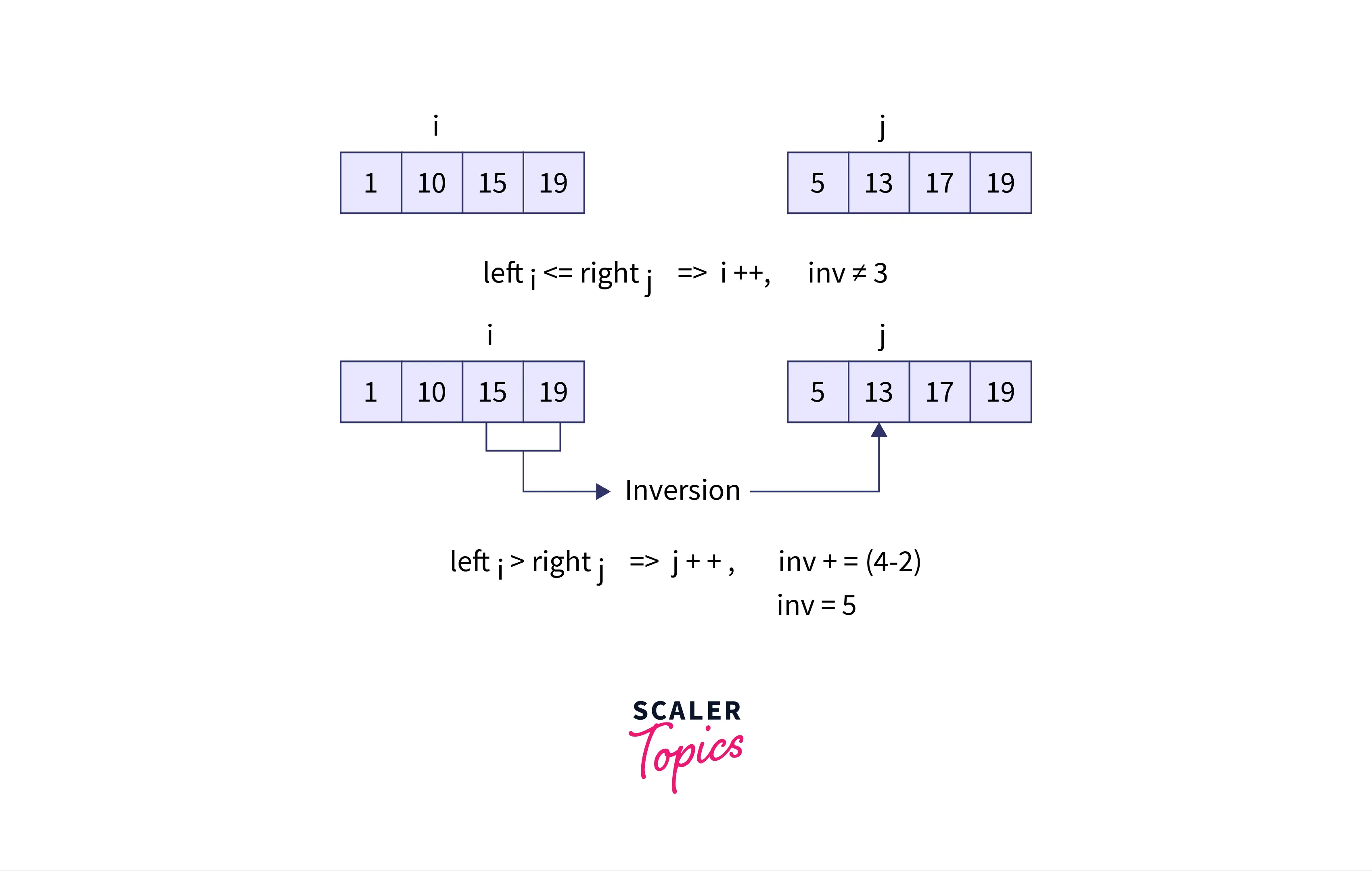
Iteration 5:

$i = 2, j = 1 \Rightarrow Left[i] > Right[j]$ $inversion \mathrel{+}= (4 - 2)$ We add the contribution of $Left[2..3]$ with $Right[1]$. $mergedArray = [1, 5, 10, 13], inversion = 5$

Iteration 6:

$i = 2, j = 2 \Rightarrow Left[i] <= Right[j]$ $mergedArray = [1, 5, 10, 13, 15], inversion = 5$

Iteration 7:

$i = 3, j = 2 \Rightarrow Left[i] > Right[j]$ $inversion \mathrel{+}= (4 - 3)$ $mergedArray = [1, 5, 10, 13, 15, 17], inversion = 6$

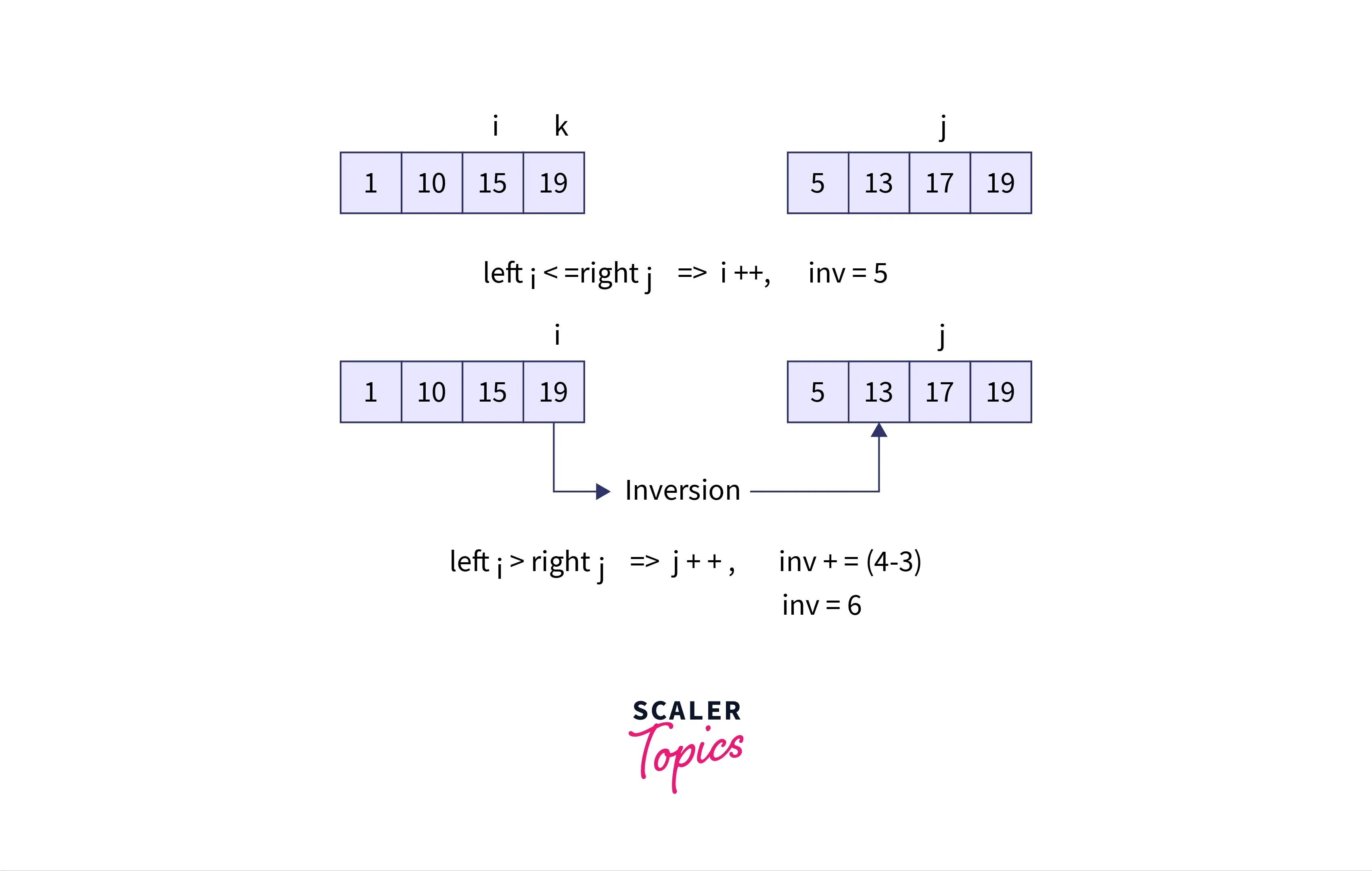
Finally we add the remaining elements. We get: $mergedArray = [1, 5, 10, 13, 15, 17, 19, 19], inversion = 6$ In this way, we calculate the count of inversion pairs while computing the merged array.

Algorithm

MergeSort(arr, start, end)

• Divide the array arr into two halves: left and right.
• Assign mid = (start + end)/2
• $invLeft$ = MergeSort(arr, start, mid)
• $invRight$ = MergeSort(arr, mid + 1, end)
• $crossing\_inv$ = Merge(arr, start, mid, end)
• return $invLeft + invRight + crossing\_inv$

Merge(arr, start, mid, end):

• Initialize $inv = 0, temp = [], p1 = start, p2 = mid$
• while $p1 < mid$ and $p2 < end$:
  • If $arr[p1] <= arr[p2]$:
    • Append $arr[p1]$ to temp
  • Else:
    • Append $arr[p2]$ to temp
    • Increment $inv$ by $(mid - p1)$
  • return $inv$

Now let us look at the implementation. We will implement this by modifying the Merge Sort algorithm to find the inversion count as discussed in the algorithm above.

C++ Implementation

Java Implementation

Python3 Implementation

Complexity Analysis

Time Complexity

In this method, we are dividing a given array into two equal parts recursively and calculate the inversion count in the two halves separately. Then we are calculating the crossing inversions using the Merge function described above. So we can the recurrence relation as: $T(N) = 2 * T(N/2) + N$. We can solve this as:

T(N) = 2T(N/2) + N
     = 2(2T(N/4) + N/2) + N  
     = 4T(N/4) + N + N  = 4T(N/4) + 2N
     = 8T(N/8) + 3N
     ... 
     ...
     = N*T(1) + log2(N)*N
     = O(N*log2(N))

Time Complexity: $O(N log(N))$

Space Complexity

In this method, in the Merge function, we are using a temporary array to merge the two halves of array A. At any recursive call, the size of the temporary array is bounded by the size of the array $A$, so we need at most $O(N)$ memory for the temporary array. We are also doing a recursion. The maximum recursion depth is bounded by $O(log(N))$. Hence total memory needed is $O(N + log(N))$ Space Complexity: $O(N)$

Approach 3: Using Heap Sort + Bisection

In the above methods, to find the inversion pair $(i, j)$, we guaranteed that $(i < j)$ and then we counted all the pairs such that $A[i] > A[j]$ efficiently. In this method, we will see a different approach. Suppose for all elements $A[i]$, we know the number of inversions contributed by this element $A[i]$, then the inversion count will be equal to the sum of all such contributions for all elements $A[i]$ of the array $A$.

Example:

$A = \{5, 4, 2, 3, 1\}$ $A[1] = 5$ contributes $4$ inversion pairs. $A[2] = 4$ contributes $3$ inversion pairs. $A[3] = 2$ contributes $1$ inversion pair. $A[4] = 3$ contributes $1$ inversion pair. $A[5] = 1$ contributes $0$ inversion pair. Total number of inversions in $A$ = $(4 + 3 + 1 + 1 + 0) = 9$.

To implement such kind of method, we need to find the contribution of each element $A[i]$ efficiently.

Suppose we have an element $A[i]$ and consider an array $index$ that stores the positions of all elements that are less than $A[i]$ in sorted order. Now, think about how will you find the inversion pairs for this element $A[i]$ assuming you are given the array $index$.

Example:

$A = \{5, 4, 2, 3, 1\}$ $A[i] = 4$. We want to find the number of inversions for element $A[2] = 4$. $index = \{3, 4, 5\}$. $index$ contains positions of all elements in $A$ that are smaller than $A[i]$. Now we know that position of $A[i] = 4$ is $i = 2$ and $index$ represent indices of all elements smaller than $4$, so we need to find such number of indexes $pos$ in the array $index$ such that $pos > i$.

To do this, we can use binary search on the array $index$. We know that any element in the array $index$ represents the position of elements in $A$ that are smaller than $A[i]$. So we just need to find the number of elements in the array $index$ that is greater than the position $i$. This means if we find the smallest position $pos$ in the array $index$ such that $(index[pos] > i)$, then all the elements whose position is $index[pos]$, $index[pos + 1]$, and so on, will form an inversion pair with the current element $A[i]$.

We do this for all elements $A[i]$ in a bottom-up fashion. This means we will calculate the contribution of each element $A[i]$ in sorted order. This allows building the array $index$. To calculate the contribution of $A[i]$, we need to guarantee that when we are finding the number of inversions for an element $A[i]$, then the index of all the elements that are smaller than $A[i]$ has been inserted into the array $index$. This is why we will consider $A[i]$ in sorted order. Now, we will add the contribution of each element to the answer. In this way, we can calculate the inversion count for the given array.

Let us understand this using an example.

Example

$A = \{5, 3, 2, 4, 1\}$, $index = \{\}$, $inversion = 0$ We will consider elements in increasing order.

Iteration 1: Smallest element = $A[4] = 1$. We will find the position of 4 in the array index using binary search. $Pos = 0$ Now we will insert this index 4 at that position and increment the count of inversions by $(size(index) - Pos)$. $index = \{4\}, inversion = 0$

Iteration 2: Next smallest element = $A[2] = 2$. $Pos = 0, inversions \mathrel{+}= (size(index) - 0)$ Pos will be 0 as 2 is smaller than 4 in the array index in sorted order. inversions = 1 (This indicates we added the contribution of the inversion (2, 4)). $index = \{2, 4\}, inversion = 1$

Iteration 3: Next smallest element = $A[1] = 3$. $Pos = 0$ as 1 is smallest element in index. $inversions \mathrel{+}= 2$ (Contribution for (1, 2) and (1, 4)). $index = \{1, 2, 4\}, inversions = 3$

Iteration 4: Next smallest element = $A[3] = 4$ $Pos = 2$ $index = \{1, 2, 3, 4\}, inversions = 4$

Iteration 5: Next smallest element = $A[0] = 5$ $Pos = 0$ $index = \{0, 1, 2, 3, 4\}, inversion \mathrel{+}= 4$ Total number of inversions = 8

This method can be implemented in many ways, one of which is using heap sort and binary search. To simulate the array $index$, we need some kind of data structure that can maintain a sorted order and allows the insertion of new elements. For this, we can use a min-heap as insertion is fast and we can perform a binary search on the heap.

Algorithm

• Create an empty array $arr$ containing $(A[i], i)$ for all elements in $A$.
• Sort $arr$.
• Create a min-heap $index$ and initialize $inversion\_count$ to 0.
• For each element $x, i$ in $arr$:
  • Find the position $pos$ of $x$ in the array $index$ using binary search.
  • Increment $inversion\_count$ by $size(index) - pos$
  • Insert $i$ into the array index.

Python3 Implementation

Complexity Analysis

Time Complexity

In this method, we use sorting first to sort the elements of array A with their indexes. Now, we iterate over each element and find the contribution of each element $A[i]$ using binary search. Iteration over the array $A$ takes $O(N)$ time and the binary search will take $O(log(N))$ time. So total time complexity = $O(N log(N))$, where N is the number of elements in the input array $A$. Time Complexity: $O(N log(N))$

Space Complexity

In this method, we need extra memory for the heap and to create temporary sort indexes depending upon the elements, so the space complexity is $O(N)$, where N is the number of elements in the input array $A$. Space Complexity: $O(N)$