Josephus Problem

Problem Statement
There is n number of people standing in a circle. Numbering starts from 1 to n and is in the fixed clockwise direction. In each step, we are supposed to eliminate a person which is at the position from the current position such that only one man remains at the end who is to be given freedom.
The counting starts from 1, k-1 people are skipped and person is to be removed. Again counting starts from person, k-1 people are skipped and person from the current position is removed. This process is repeated until only one man is remaining in the circle.
The input consists of two integers n and k where n is the number of people in the circle and using the k position for eliminating the next person is calculated. k-1 people are skipped from the current position and person is to be killed.
The output is an integer greater than zero and less than or equal to n. This integer is the safe position for the person to stand at as only the last person survives.
Constraints
The values of n as well as k are greater than or equal to 1 and are less than or equal to .
Constraints: 1 <= n, k <=
Example
Let us dive into an example of a Josephus problem.
Input:
Output:
Example Explanation
Initially, 5 people are standing in the circle as follows:
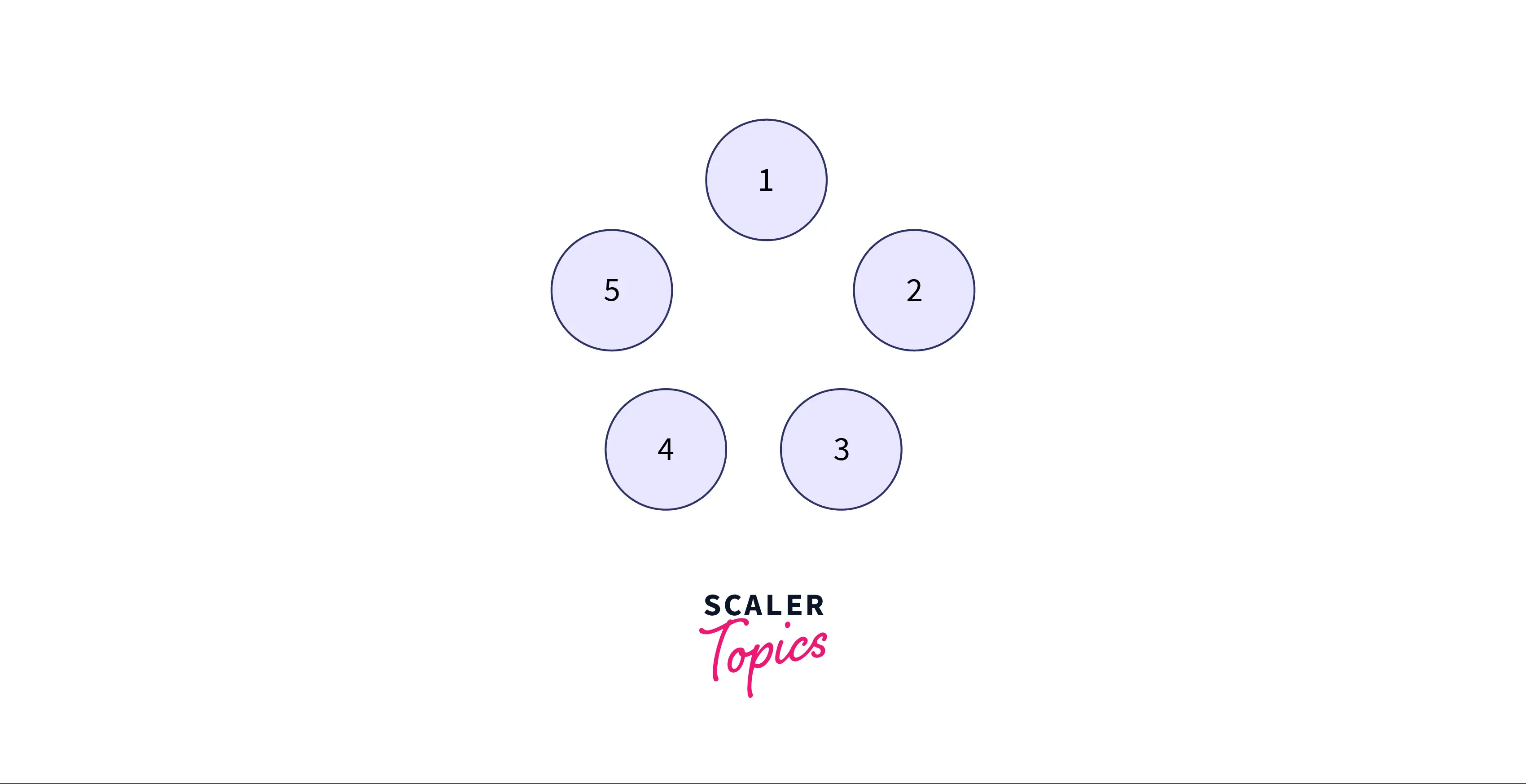
Now starting from position we will skip k-1 people and kill the kth person. Out k in the example above is 3 so the person to be killed is 3rd person.
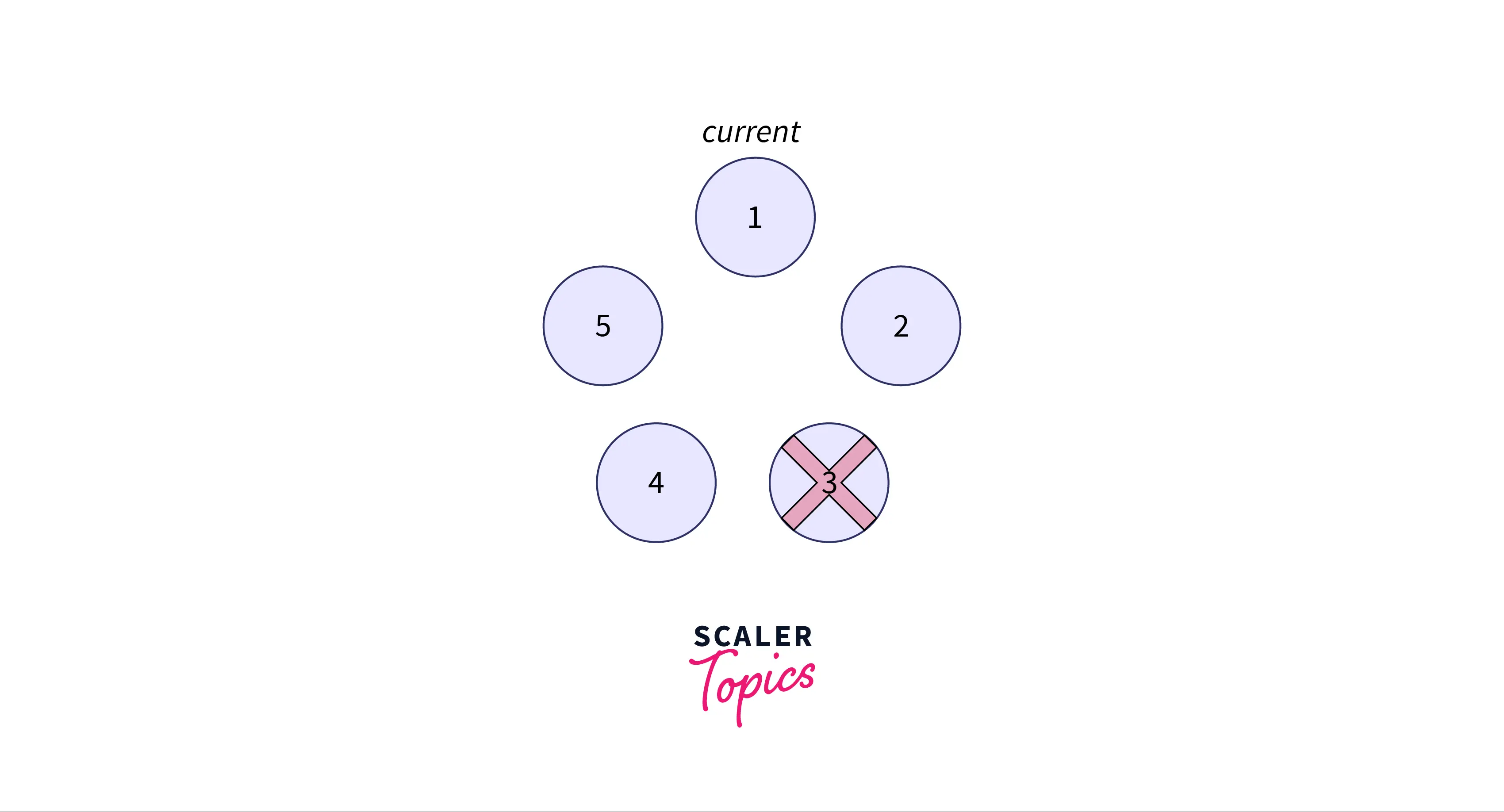
Next, our current becomes the person in the circle, we go from 4 to 5 and back to 1 which is person is killed.
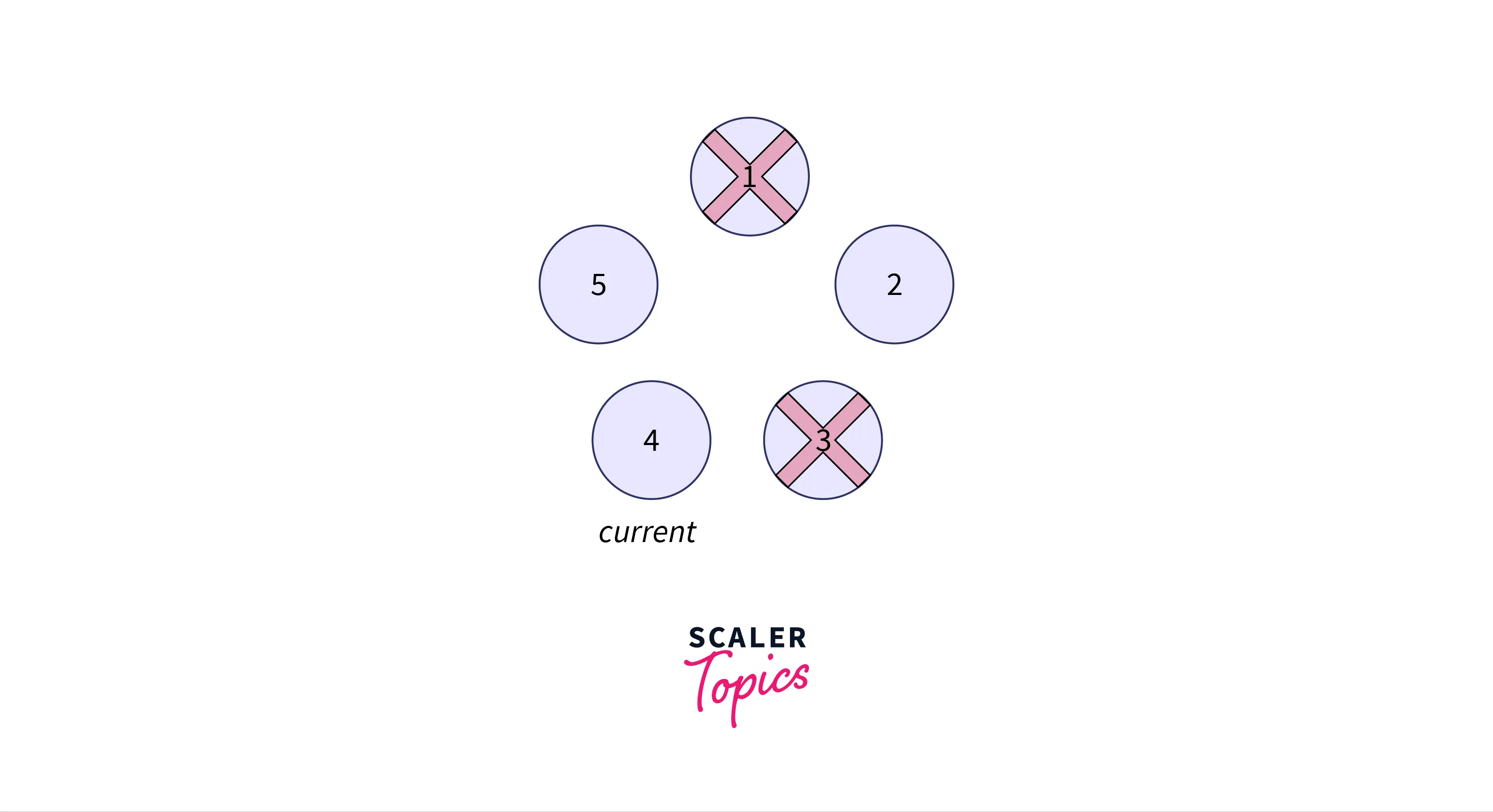
Now the current is person, we don't consider person as it is already killed. The next person is and person is killed.
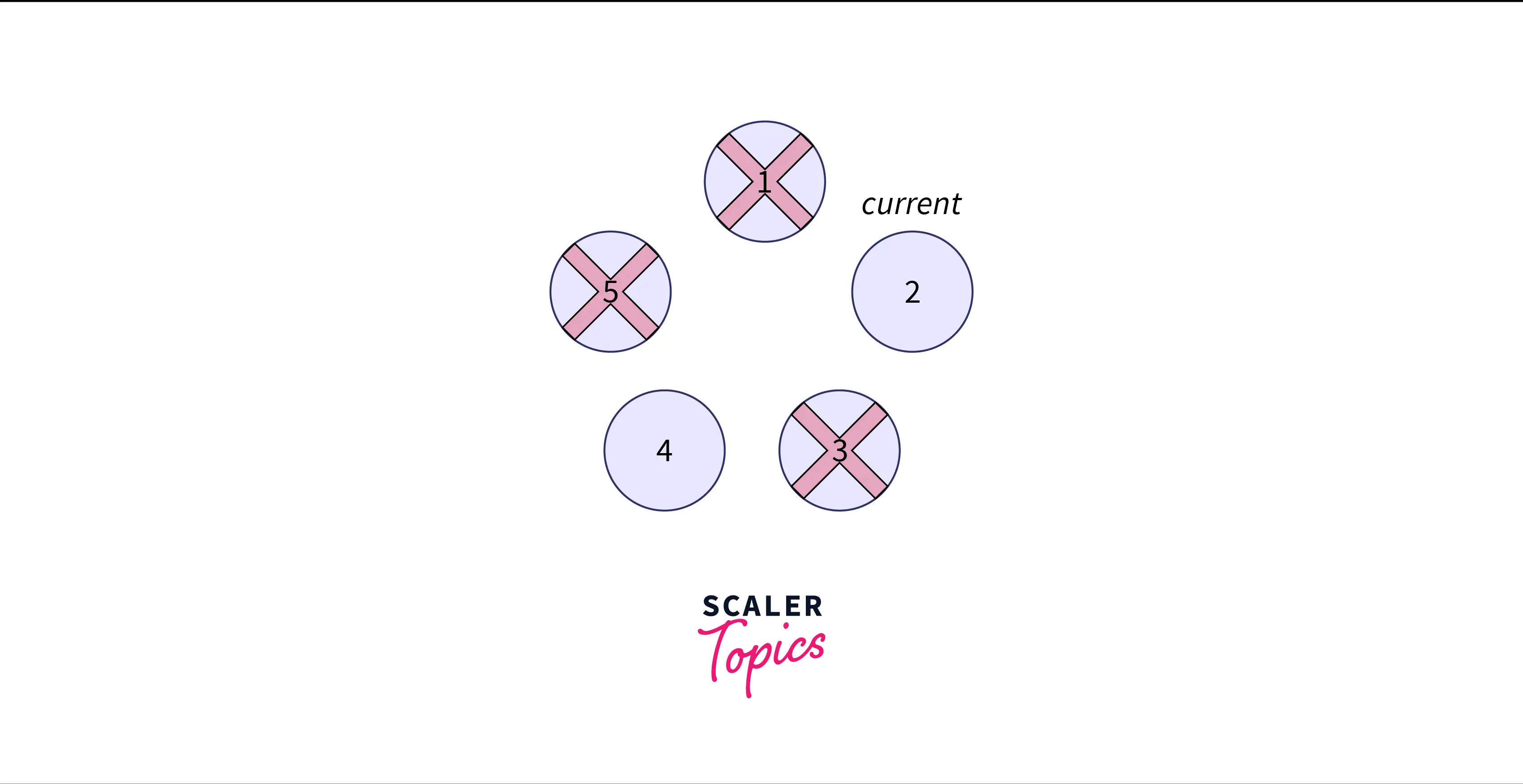
Again the current is person and we go to person and back to person. Thus, person is killed in this step.
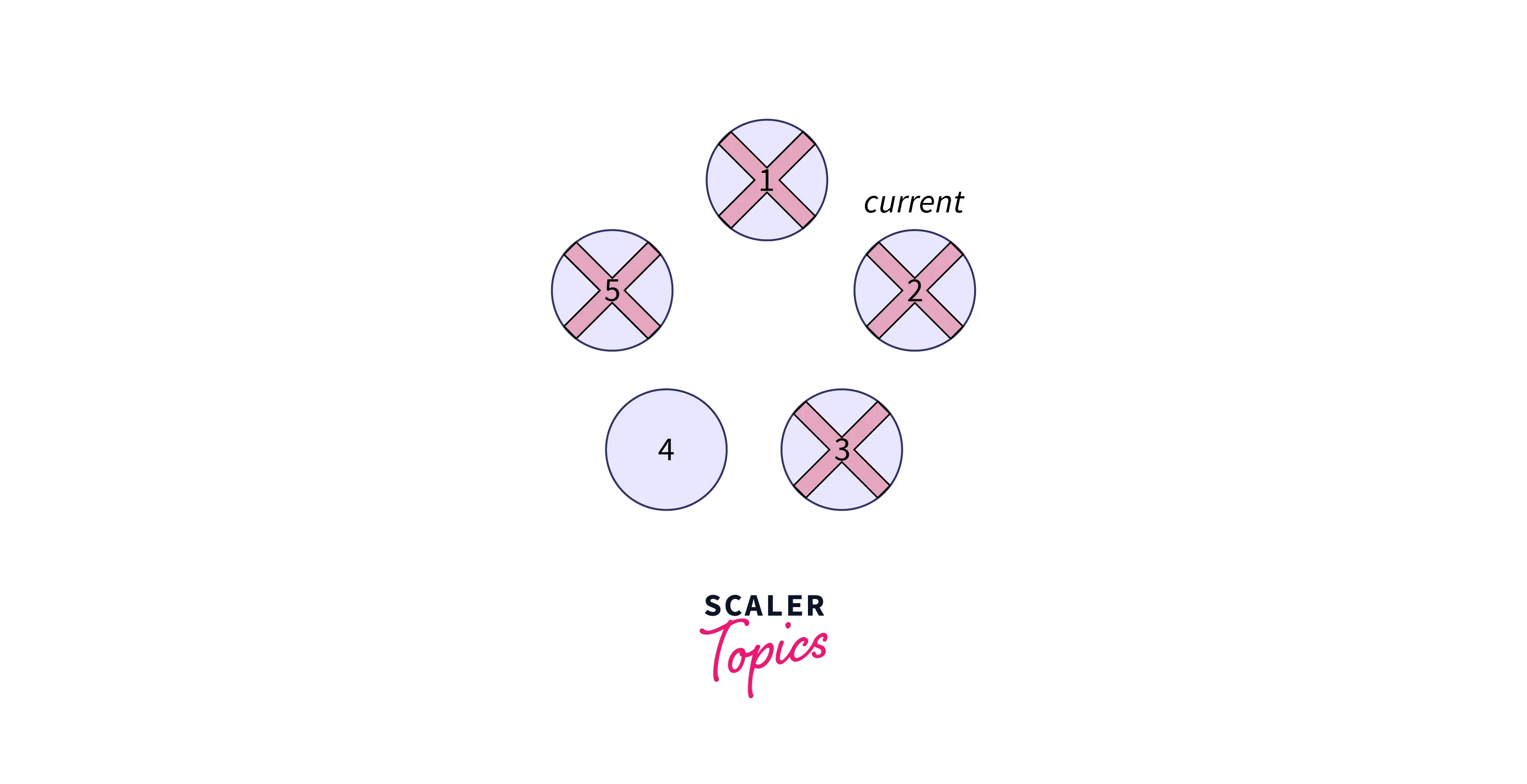
Now, only one of the last people is remaining which is the person in the position. This is the required output, it is the safe position as person will be the last one remaining to survive.
Approach 1: Recursive Structure (Code in Java, Python, C++)
A simple approach is to use recursion. Recursively we call the Josephus problem() function for eliminating a person from the group at a certain position and decrementing the number of people in the group with each call until the last person is left. There are n people in the group, and person is to be killed from the current position. Once the first person is killed, n-1 people are left. So we call the Josephus function for n-1 and k. Then from n-1, k to n-2,k and so on until n==1 which forms our base case.
The position returned by the Josephus function when n equals 1 is 1, irrespective of the value of k as there is only one person left. So this becomes our base condition for the recursive function. Now we are required to find the formula for the recursive call. Let us apply brute force to find the values for n from 1 to 10 and k as well from 1 to 10.
| n/k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 3 | 3 | 2 | 2 | 1 | 1 | 3 | 3 | 2 | 2 |
| 4 | 4 | 1 | 1 | 2 | 2 | 3 | 2 | 3 | 3 | 4 |
| 5 | 5 | 3 | 4 | 1 | 2 | 4 | 4 | 1 | 2 | 4 |
| 6 | 6 | 5 | 1 | 5 | 1 | 4 | 5 | 3 | 5 | 2 |
| 7 | 7 | 7 | 4 | 2 | 6 | 3 | 5 | 4 | 7 | 5 |
| 8 | 8 | 1 | 7 | 6 | 3 | 1 | 4 | 4 | 8 | 7 |
| 9 | 9 | 3 | 1 | 1 | 8 | 7 | 2 | 3 | 8 | 8 |
| 10 | 10 | 5 | 4 | 5 | 3 | 3 | 9 | 1 | 7 | 8 |
As it is a recursive function we will be calling it for smaller operations i.e. . The result that we get from the smaller problem needs to be adjusted. To make adjustments in the position we add k-1 to it. As we are adding, the position may be greater than n which may cause the error. Also, all the people are standing in a circle. So, we simply take modules to get an effective position. As we are using one-indexing i.e. position of the first person starts from one we add 1 to the result. The pattern so formed is
Let's take the same example of n=5 and k=3, using the above formula: n=1, k=3:
n=2, k=3:
n=3, k=3:
n=4, k=3:
n=5, k=3:
Recursively, we go from 5 to 1 and reach to the solution which is the same as the brute force approach. Let us apply the same formula in the algorithm:
Java Implementation
C++ Implementation
Python Implementation
Output:
Complexity Analysis
Time Complexity
The time complexity for the recursive solution is **O(n)** as if n is greater than 1, the Josephus problem function is called by decreasing the value of n by 1 i.e. n-1 until n is not equal to 1. The function will be called as - josephusProblem(n, k), josepusProblem(n-1, k), josephusProblem(n-2, k) ..., josephusProblem(2, k), josephusProblem(1, k). Thus, it is called n times and the time complexity for the same is O(n).
Space Complexity
The space complexity for this solution is O(n) as the call sequence which led to this state would be f(n)->f(n-1)->f(n-2)->...->f(1). The result of these are stored in the stack frames in the memory and when f(n) is called it calls all the previous function calls and then calculates the current value and returns it. After which it is removed from the memory.
Approach 2: Using List (Code in Java, Python, C++)
Another approach is using lists which is very much similar to the brute force approach. In this approach, we iteratively remove the person at the position from the current position. We first change the value of the current position as pos = (pos+k-1)%n, remove the person at the current position, and decrement the value of n until our n is not equal to 1. In other words, we remove the element of the list at the index pos.
The algorithm for the same is as follows:
**Note: ** Here, n is the index in the list respectively. Let us see an example where n = 8 and k = 3.
The list initially is as follows: [1, 2, 3, 4, 5, 6, 7, 8]
In the first iteration
| Iteration no. | k | n | pos | position removed | list |
|---|---|---|---|---|---|
| Initially | 3 | 8 | 0 | - | [1, 2, 3, 4, 5, 6, 7, 8] |
| 1 | 3 | 8 | 2 | 3 | [1, 2, 4, 5, 6, 7, 8] |
| 2 | 3 | 7 | 4 | 6 | [1, 2, 4, 5, 7, 8] |
| 3 | 3 | 6 | 0 | 1 | [2, 4, 5, 7, 8] |
| 4 | 3 | 5 | 2 | 5 | [2, 4, 7, 8] |
| 5 | 3 | 4 | 0 | 2 | [4, 7, 8] |
| 1 | 3 | 3 | 2 | 8 | [4, 7] |
| 1 | 3 | 2 | 0 | 4 | [7] |
Thus at the end, only position is remaining.
Java Implementation
C++ Implementation
Python Implementation
Output:
Complexity Analysis
Time Complexity
The time complexity for this algorithm is O(n) as we are iterating through the loop for each person in the circle.
Space Complexity
In the algorithm above we are using an extra list for saving all the positions in a list which accounts for the additional space and thus occupies O(n) space.
Conclusion
- There are two approaches usually used to solve the Josephus problem.
- The first one is using recursion, n=1 is the base condition and we return 1. The formula for the rest of the cases is .
- The other solution is using the list. We first insert all the positions in the list and remove all the people at the position until only one person is remaining .
FAQs
Q: Which data structure is used to solve the Josephus problem?
A: The List data structure is used to solve the problem usually. It is used to store all the positions from 1 to n. We can also use recursion to solve the problem.
Q: What is the brute force approach to solve Josephus's problem?
A: The Josephus problem can be solved by eliminating the person at the position iteratively and recursively until only one person is remaining .
Q: What is the best complexity we can achieve and use which approach?
A: We can have O(n) time complexity and O(n) space complexity at least using both the approaches i.e. the list as well as the recursion approach.
Q: What is the special case of this problem?
A: k=2 is the special case of this problem. It becomes very much easier to solve it with less amount of recursive calls as well as lesser time complexity.
-
case I: n is even If n is even then all the even positions i.e. 2, 4, 6, ..., n-2, and n are eliminated as k is 2 and the problem is remaining only for n/2 number of positions i.e. 1, 3, ..., n-1. Also, we are required to adjust the positions by shifting as follows:
-
case II: n is odd Similarly, when n is odd, all the even numbers i.e. (n-1)/2 are again crossed out. The remaining problem is for (n+1)/2, taking into account the shift of positions we obtain the following formula:
Common formula We can rather use a simpler formula, which is applicable for both cases:
