Kosaraju Algorithm

Problem Statement

Find all strongly connected components in O(V+E) time using Kosaraju’s algorithm.

Strongly connected Component(SCC) - In a directed graph a strongly connected component is a component of the graph in which there is a path between every pair of vertices.

Example

Example of strongly connected component in a graph :

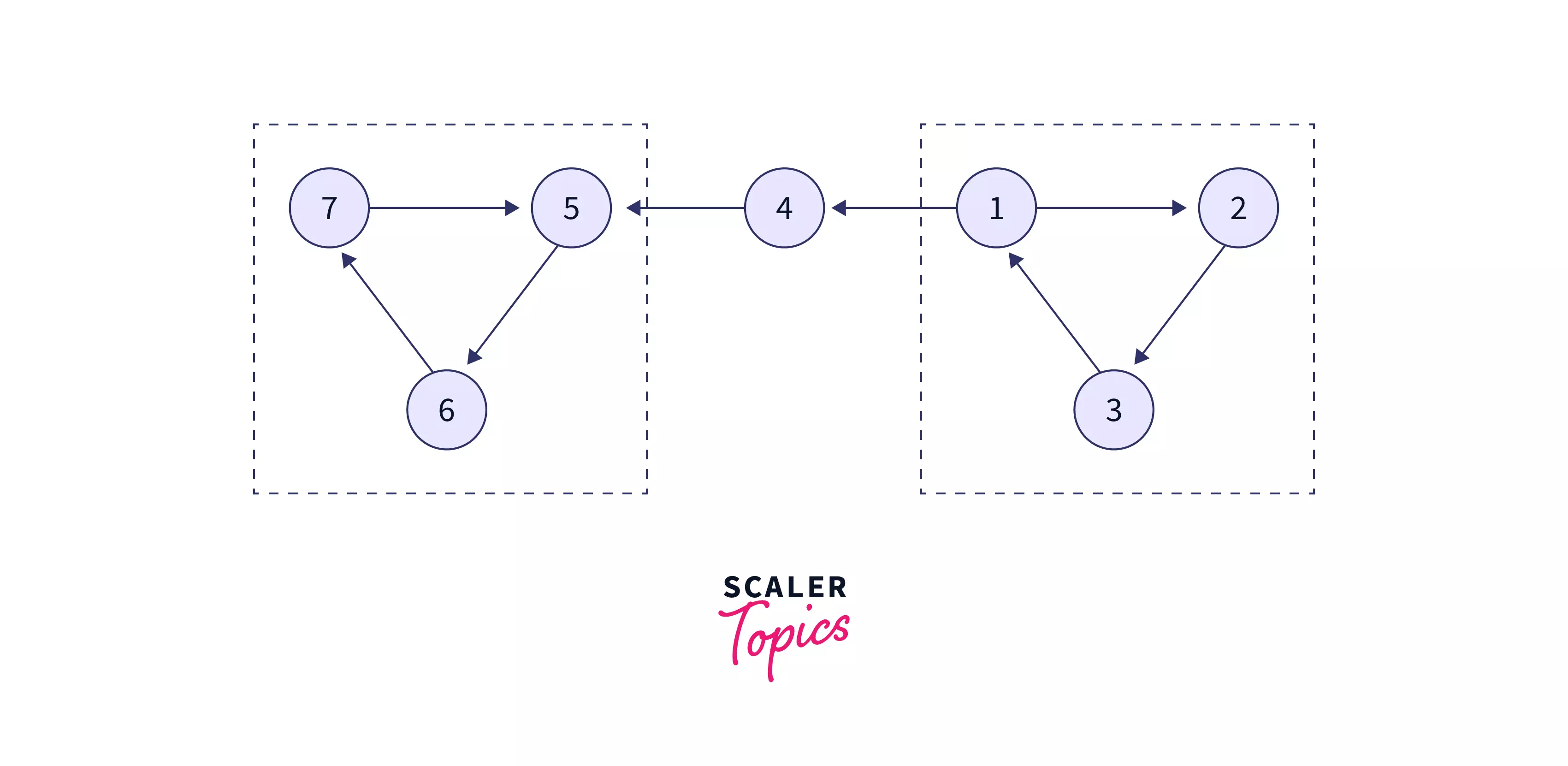
Example Explanation

In the above Example diagram the directed graph contains three strongly connected component.

1. the vertex group of (7,5,6) in which there is a path between every pair of vertices.
2. 4 - single vertex
3. The vertex group of (1,2,3) in which there is a path between every pair of vertices.

In the above example we can see that a single vertex is also considered as a strongly connected component. As kosaraju Algorithm finds the minimum number of strongly connected component in directed graph so the answer to the above example will be 3.

Input/Output

Input - Given Number of vertices = N, and number of edges of the directed graph = M and the weight of the M edges.

Output - Number of strongly connected component in the given directed graph.

Kosaraju's Algorithm

Intution - The intution behind Koasaraju algorithm is to perform DFS in the directed graph such that one DFS call would be able visit all the vertices of a strongly connected component in the graph.

Algorithm Steps :

• Depth First traversal(DFS) is done on the graph and when DFS traversal is done recursively on adjacent vertex of the graph, the vertex are pushed to an empty stack one by one.
• Find the transpose of the graph by reversing the direction of every edge in the directed graph.
• Pop the vertex from the stack one by one and do DFS on the popped out vertex "v". The DFS will print the stronlgy connected component of "v".

Implementaion in C++ :

Impelementation in Java :

Implementaion in Python :

Output of All Above Programs:

Time Complexity : In kosaraju algorithm mainly three steps takes place :

1. DFS is called : Time taken to perform DFS on graph represented by adjacency list is O(V+E).
2. graph represented by adjacency list is reversed: For reversing the graph represented using adjacency list we have to iterate over the adjacency list which will take O(V) time.
3. Again DFS is called : TIme taken for DFS on graph represented by adjacecny list is O(V+E)

So, the total time taken in all the three steps in kosaraju algorithm is O(V+E) +O(V) +O(V+E) = O(V+E)

So, the time comlexity of the kosaraju algorithm is O(V+E).

Space Complexity : As kosaraju algorithm uses stack to store the vertices while performing first DFS so the space used by stack is equal to size of the vertices of the graph. So, the time complexity of kosaraju's algorithm is O(N), where N is the total no of vertices in the graph.

Strongly Connected Components Applications

1. Strongly connected components SCC are used in social media algorithms where SCC is used to know the persons with common interest and common friends.
2. Strongly connected components are used in maps algorithm to link the path with similar origin and destination.
3. Strongly connected components are also used in vehicle routing algorithms.