Largest Subarray with 0 Sum

Problem Statement

Given the array $ar[]$ of size, $n$ has positive and negative integers. From the array $ar[]$, find the length of the largest subarray having a 0 sum.

As we have to find the length of the largest subarray. So, first of all, it is required to understand what is a subarray

Example

Let us understand the largest subarray with the 0 sum problem with the examples.

Example : 1

Output :

Example : 2

Output :

Example Explanation

We are required to find all the subarrays starting from the ith index and ending with the jth index where $0<=i<n$ and $i<=j<n$ where $n$ represents the length of the array.

Example : 1

First of all, we will find the sum of every subarray of the input array $ar[]$.

Here the size of the array is 7 so we are required to find the sum of all the subarrays starting from the ith index and ending with the jth index where $0<=i<7$ and $i<=j<7$.

Refer to the below image for the explanation of Example1 :

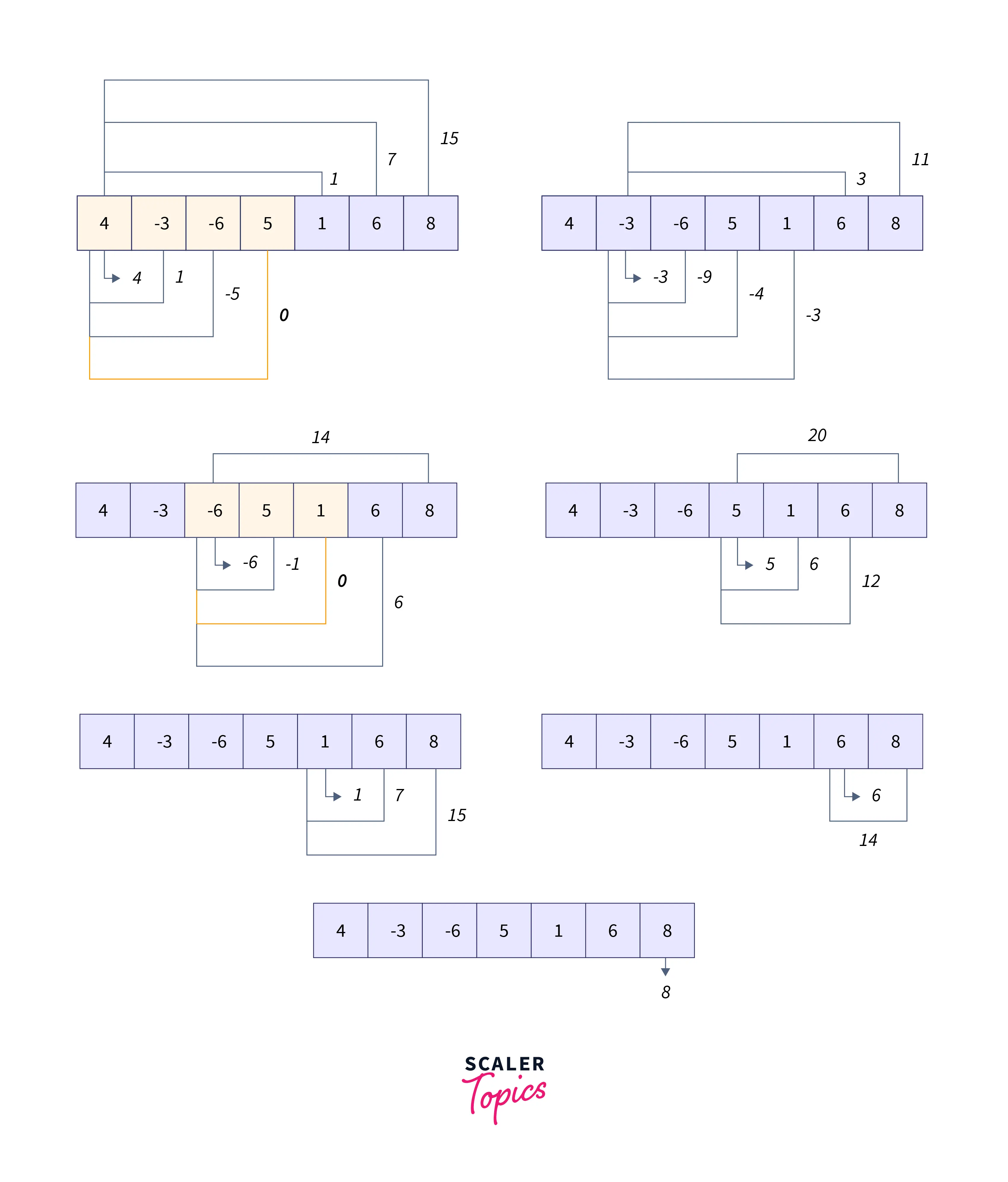
Subarrays with 0 sum are : $[-6,5,1]$ with length 3 and $[4,-3,-6,5]$ with length 4.

So the maximum length of subarray with 0 sum is 4.

Example : 2

First, we will find the sum of every subarray of the input array ar[]. Here in the example, the size of the array is 8 so we are required to find the sum of all the subarrays starting from the ith index and ending with the jth index where $0<=i<8$ and $i<=j<8$.

Refer to the below image for the explanation of Example2 :

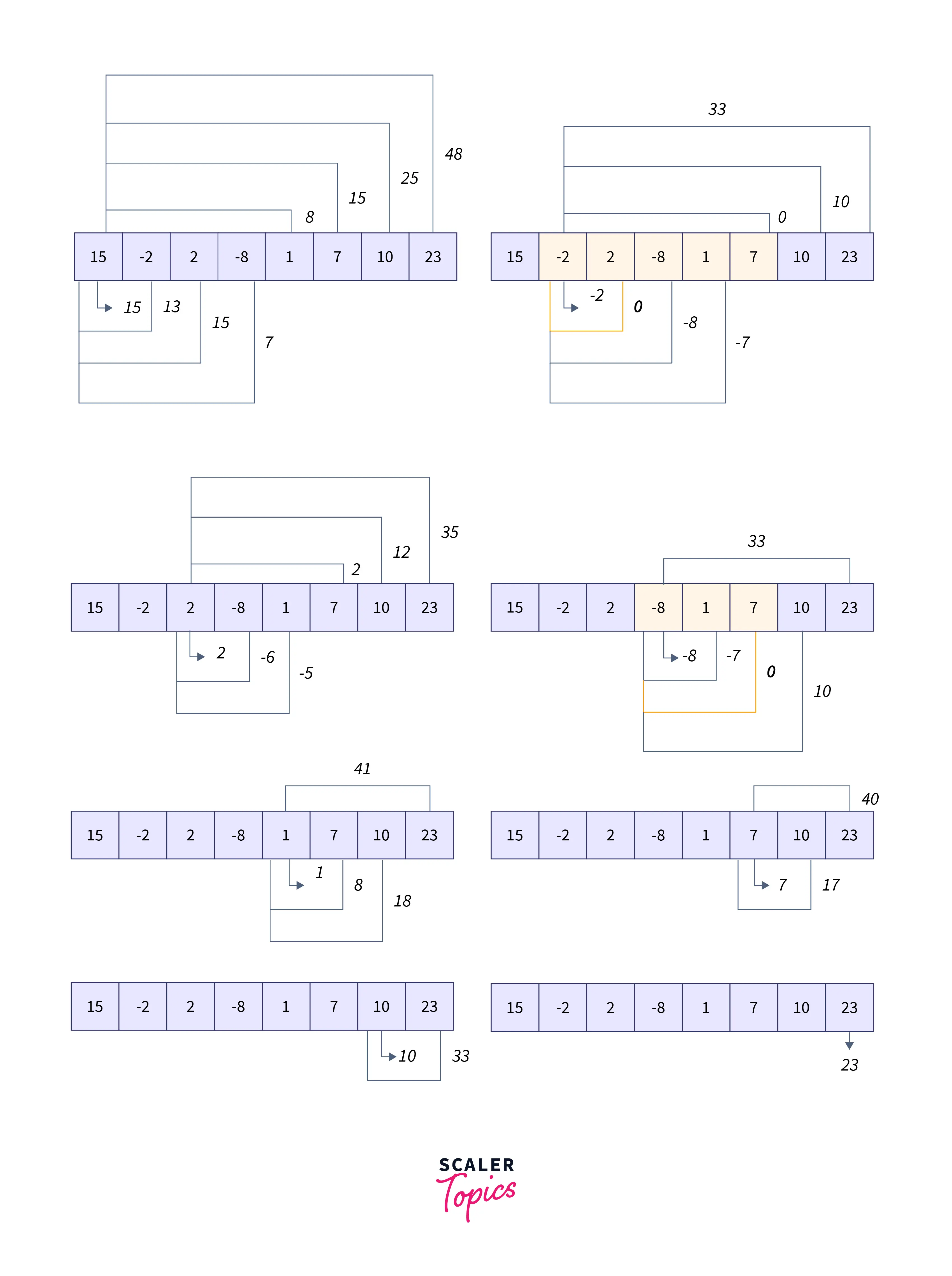
Subarrays with 0 sum are : $[-8,1,7]$ with length 3 , $[-2,2,-8,1,7]$ with length 5, $[2,-2]$ with length 2.

So the maximum length of subarray with a 0 sum is 5.

Input :
Given a positive integer n which represents the size of an array $ar[]$. And the n positive/negative integers represent the elements of $ar[]$.

Output :
You have to return the length of the largest subarray that has a sum of 0.

Constraints

The constraints for the largest subarray with a 0 sum problem are given below : $1 <= n <= 100000$,
$-1000 <= ar[i] <= 1000$, for i in range 0 to $n$.

Approach 1 : Brute Force Approach - Using Three Nested Loops

Approach

We will consider all the subarrays of the input array and find the sum of every subarray and check the sum of every subarray. And then, store the length of the longest subarray among all the subarrays that have a sum of 0 and return the longest length as a result.

Transform Your Career

Choose from our industry-leading programs designed for career success

NSDC Certified

Modern Software and AI Engineering Program

Master full-stack development with AI integration

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Modern Data Science and ML with specialisation in AI

Advanced data science techniques with AI specialization

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Advanced AIML with Specialisation in Agentic AI

Deep dive into AIML with focus on Agentic systems

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

DevOps, Cloud & AI Platform Engineering

Build and manage AI-powered cloud infrastructure

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

AI Engineering Advanced Certification by IIT-Roorkee

Premier AI engineering certification from IIT-Roorkee

3 MonthsDuration

AI-LedCurriculum

Career SupportSupport

Go to Program

Algorithm

1. Declare and initialize a variable max_length $= 0$, which stores the length of the largest subarray with 0 sum.
2. Start traversing an array from the start.
3. For every index i of the array, start a nested loop with variable j that ranges from i to the size of the array.
4. Initialize the variable cursum $= 0$ for storing the sum of subarray starting from the ith index and ending with the jth index.
5. And then run a loop to find the sum of subarray starting with the ith index and ending with the jth index and store the sum in cursum.
6. Check if the value of cursum is 0, then check if the length of the current subarray is greater than the length stored in max_length and update the max_length with the current subarray length $i.e.$ $j-i+1$.
7. Return the max_length.

Implementation

C++ Implementation :

Output :

Java Implementation :

Output :

Python Implementation :

Output :

Time Complexity

As we run three nested loops one loop for starting index of the subarray, the second loop for the ending index of the subarray, and the third loop for finding the sum of the current subarray. So worst case time complexity of running three nested loops is $O(n^{3})$.

So worst case time complexity of this approach is $O(n^{3})$.

Space Complexity

We are not using the extra space. So worst case space complexity of this approach is $O(1)$.

Approach 2 : Efficient Brute Force - Using Two Nested Loops

Approach

This approach is an optimized version of the previous approach. In this approach, we use the brute force approach, where two nested loops are used to calculate the subarrays running sum. In two loops, the outer loop is to fix the starting index of a subarray, and the inner loop is for the ending index of the subarray while iterating the second loop, we will find the sum and store the length of the largest subarray with 0 sum.

Algorithm

1. Declare and Initialize a variable max_length $= 0$, which will store the length of the largest subarray with the sum 0.
2. Start traversing the array from starting index and initialize the variable cur_sum $= 0$ which will store the sum of the subarray starting from the ith index.
3. Traverse array from next element of current index till the end of th array and at every iteration add the current element to cur_sum.
4. Now check if cur_sum $= 0$, and check if max_length $<$ current subarray length, then update the value of max_length with current subarray length.
5. After traversing the whole array return max_length as the result.

Implementation

C++ Implementation :

Output :

Java Implementation :

Output :

Python Implementation :

Output :

Time Complexity

As we are running two nested loops, one loop for starting index of the subarray, the second loop for the ending index of the subarray, and while running the second loop, we are also calculating the running sum of the subarray.

We know that worst case time complexity of running two nested loops is $O(n^{2})$.

So worst case time complexity of this approach is $O(n^{2})$.

Space Complexity

We are not using the extra space. So worst case space complexity of this approach is $O(1)$.

Approach 3 : Alternative and Efficient Approach - Using the Hash Table

Approach

In this approach to the largest subarray with the 0 sum problem, we are using hashing for finding the length of the largest subarray. The idea of this approach is to iterate over the input array and calculate the sum of elements from starting element to the current element. And check if the current sum is present in the map, then there is a subarray with a 0 sum.

Algorithm

1. Initialize max_length $= 0$, cur_sum $= 0$ and create an empty map for storing the previous sum-index as a key-value pair.
2. Iterate over the input array.
3. At every index update sum by adding current element cur_sum $=$ cur_sum $+$ $array[i]$.
4. For every index, check if the cur_sum is on the map or not.
5. If the cur_sum is present in the map, then update the max_length to a maximum max_length and the difference between two indices (current index and index in the hash-map).
6. Otherwise, put the cur_sum as a key in the map with the index as a value.
7. Return the maximum length (max_length).

Implementation

C++ Implementation :

Ouput :

Java Implementation :

Ouput :

Python Implementation :

Ouput :

Time Complexity

As we are iterating over an input array of size n once whose time complexity $O(n)$ and while iterating, we are searching/inserting an element in the map whose time complexity is $O(1)$. So total time complexity of this approach is $O(n)*O(1)$.

So worst case time complexity of this approach is $O(n)$.

Space Complexity

As we are using a hashmap for storing the previous sums. So worst case space complexity of this approach is $O(n)$.

Comparison of Different Solutions

Comparison of time and space complexity of all approaches of solution of largest subarray with 0 sum problem is given below :