Linked List

Overview
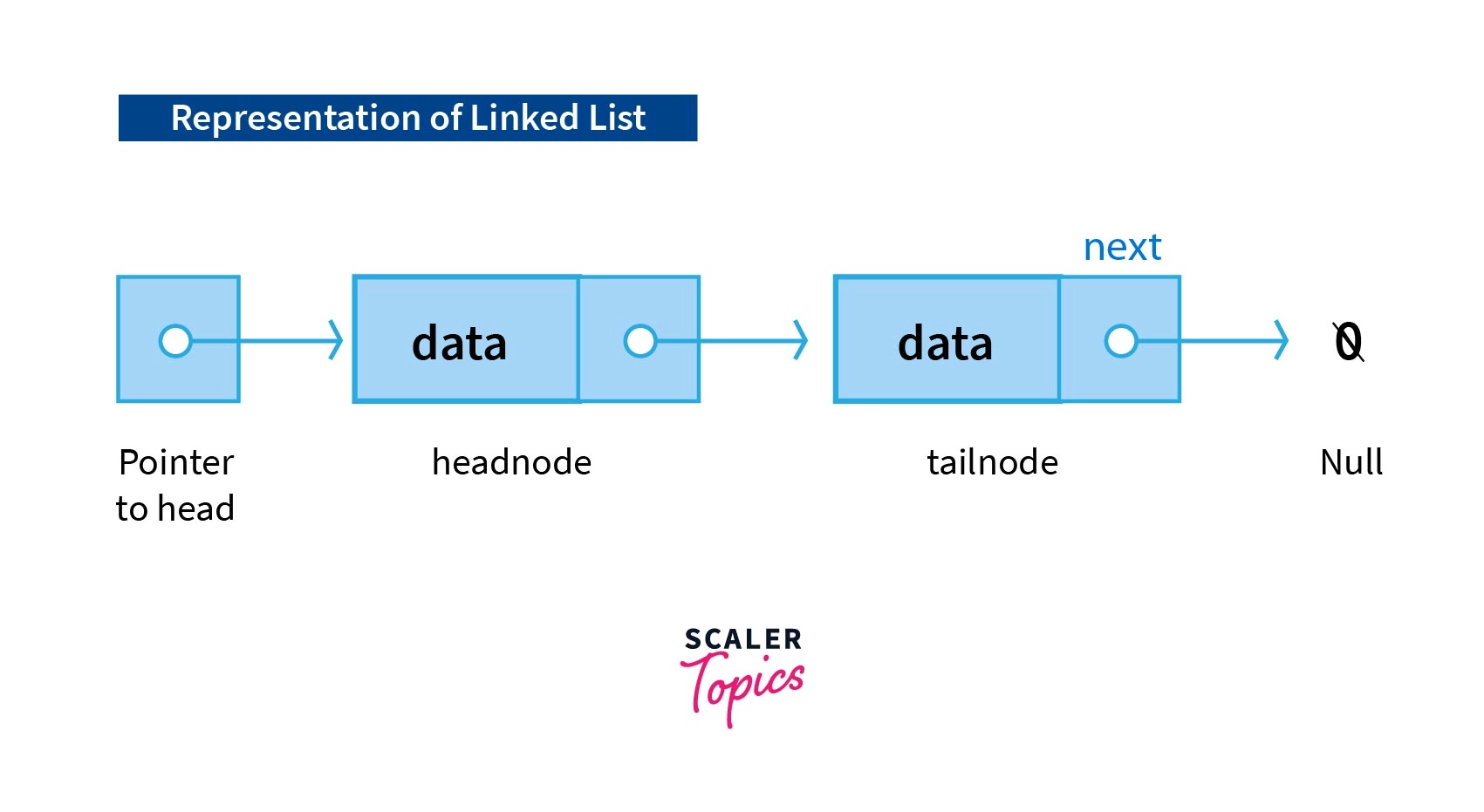
A Linked List is a linear data structure consisting of connected nodes where each node has corresponding data and a pointer to the address of the next node. The first node of a linked list is called the Head, and it acts as an access point. On the other hand, the last node is called the Tail, and it marks the end of a linked list by pointing to a NULL value!
Why Do We Need a Linked List?
Imagine going to a movie theater along with a large group of friends, only to find out there's no way to book consecutive seats to accommodate all. However, there are plenty of disjoint empty seats for that particular screen. So, you all buy tickets and sit accordingly.
But there's a catch!
Since only you were buying popcorn for all, how would you distribute that to your friends? You can't remember where everyone sat, and it's dark inside the hall.
So, instead of you remembering where everyone sat, if everyone kept track of the next friend's seat, then such reference would help popcorn tubs to traverse up to a friend who's yet to get popcorn. This could be achieved by passing popcorn to the next friend starting from you!

See how the linked list came in handy while keeping track of all these randomly distributed disjoint seats?
In a computer, you can think of memory as a movie theatre, the virtual address space as the seats, and any particular memory address as a seat number.
Note: The virtual address space refers to the address range on which a process relies in order to carry out its execution. Unlike seats, this address space is virtual and not real. It's a logical and abstracted mapping to a rather intricate physical memory.
Now, if we had initiated booking in advance, we could have booked an entire row of consecutive seats much like an array does when we declare it with a fixed size in advance, like so:
int seats[24];
In our context of a movie theater, if more friends later decide to join the group to catch the movie. We cannot simply append them to the array of seats since there might be other audiences seating just after the last allocated seat.
So either we find another larger empty row of consecutive seats so that all friends can sit together (much like dynamic array), or we rely on an approach similar to the linked list, in that we simply insert new friends in vacant spots but still have references to them should we require to pass popcorn and drinks.
You see, arrays are suitable when we need fast access. Like who's seating at seat no. 13 can be answered in constant time! But arrays require you to declare a fixed size at the compile-time, due to which memory can be either wasted or fell short.
Whereas linked list shines when we need to modify existing data by insertion and deletion because it doesn't have a fixed size. So, our memory consumption is determined at run time as the linked list shrinks and grows dynamically in constant time.
Later on, we will explore these linked list operations in-depth but first, let's discuss the types of linked lists.
Types of Linked List
There are mainly three types of linked lists:
Singly Linked List
Here, we can only traverse in one direction (not the band ) due to the linking of every node to its next node.

Doubly Linked List
Here, we can traverse in both directions as every node contains an additional prev pointer that points to the previous node.

Circular Linked List
Here, we can keep traversing forever and ever until the program crashes as the tail node's next pointer points to the head node instead of a NULL.

"That's cool, but what does a linked list look like in code" - you ask.
Well, let's see...
How Can We Declare a Linked List?
Prior to proceeding further, let me ask you one thing what the smallest linked list is possible? and don't cop out by saying NULL!
That's right, a single node.
A node that is both head and tail and in and of itself a linked list!
Hence, behold the pseudo blueprint of THE NODE (of a typical singly linked list):
where data can be any valid type and not just integer, but next must be a Node pointer.
Let's declare the head of our linked list like so:
And that's it for a single node of a singly linked list
"But how can we extend it for a linked list of size k?"
where num could be an array of integers storing the data for building our respective linked list and itr could be any variable iterating over the indices of the said array.
Operations of Linked List
Keeping the above Node's blueprint in mind, let's now discuss some trivial operations on a linked list of size 'k':
Traversal
We can traverse the entire linked list starting from the head node. If there are n nodes then the time complexity for traversal becomes O(n) as we hop through each and every node.

Insertion
Inserting a new node at a given position is achieved by manipulating at most 2 next pointers like so; consider two pointers, prevNode, and newNode
set newNode's next pointer to the prevNode's next pointer
and set prevNode's next pointer to the newNode
where prevNode denotes a pointer to the node after which newNode is to be inserted.
And since only a constant number of pointers gets changed irrespective of the size of the linked list, the complexity should have been O(1).
However, to get access at any given position, we have to traverse starting from the head till prevNode. Thus, the worst case for insertion could be expressed as;
Traversal O(n) + Just the insertion O(1) = Insertion O(n).
However, the best case would be to insert in the beginning and hence the time complexity becomes Ω(1).
Notice that the order of execution does matter in case of insertion. If we interchange the steps i.e. first set prevNode's next pointer to the newNode then we lose the reference to the remaining of the linked list previously occurring after the prevNode. Something to keep in mind!

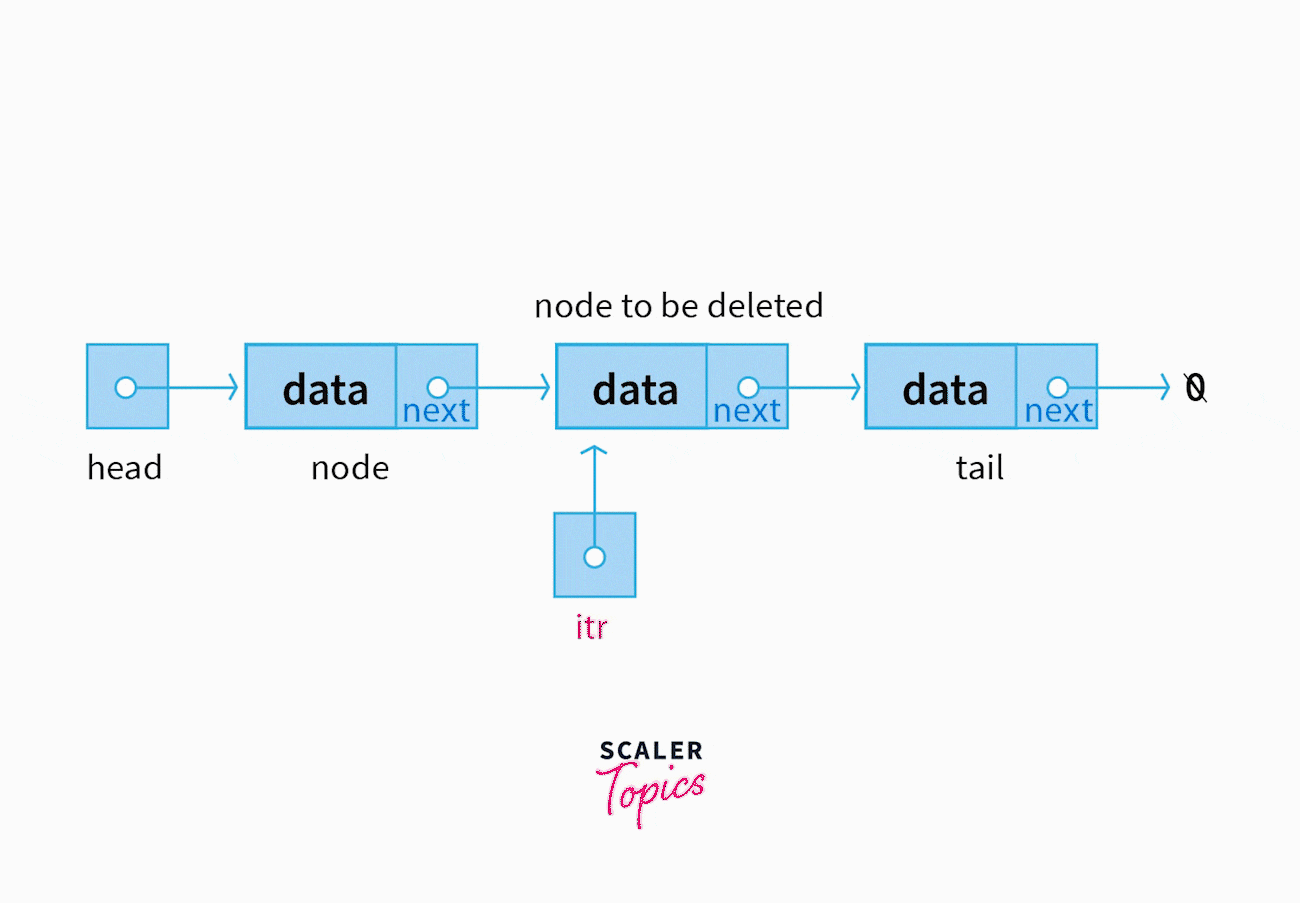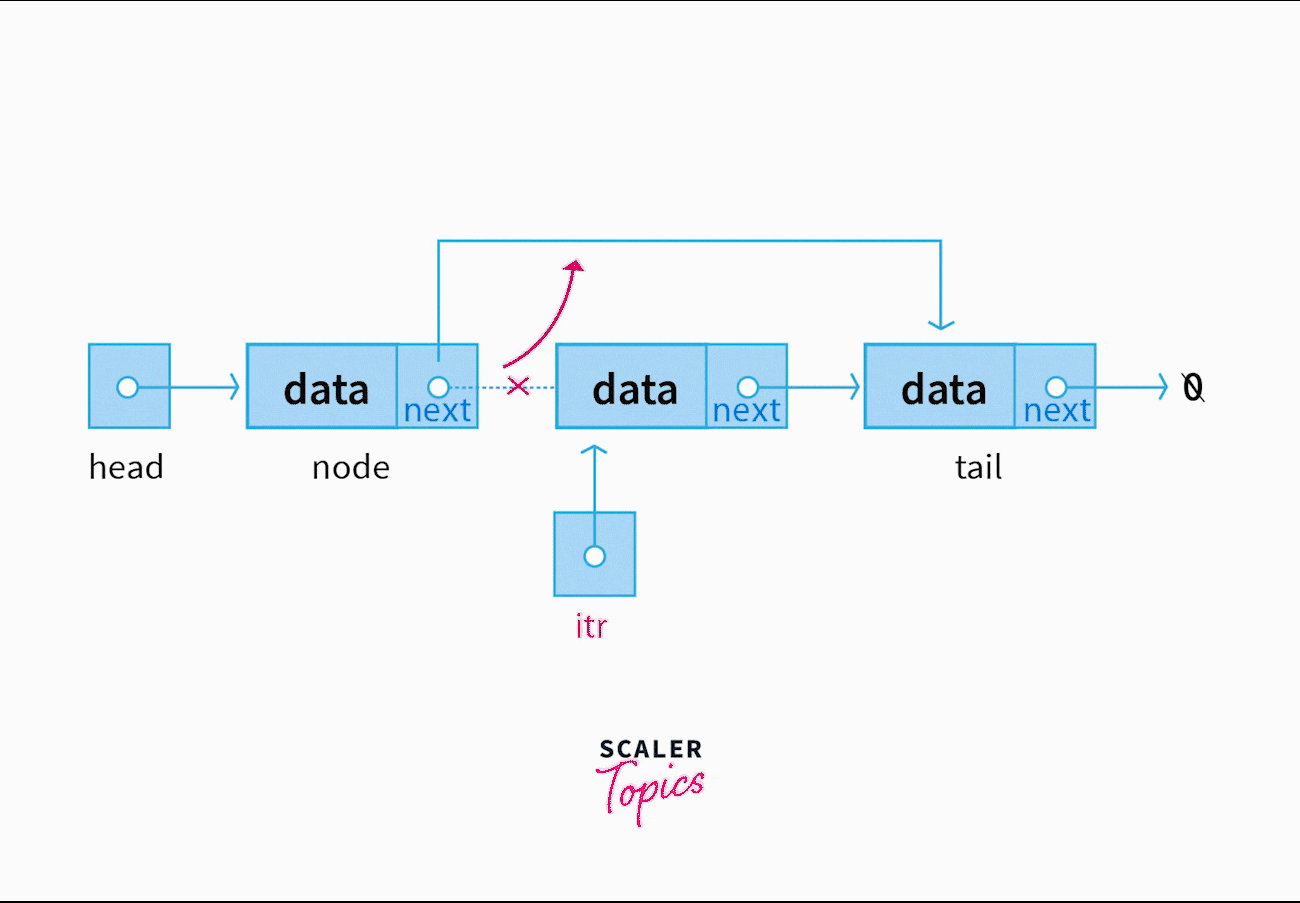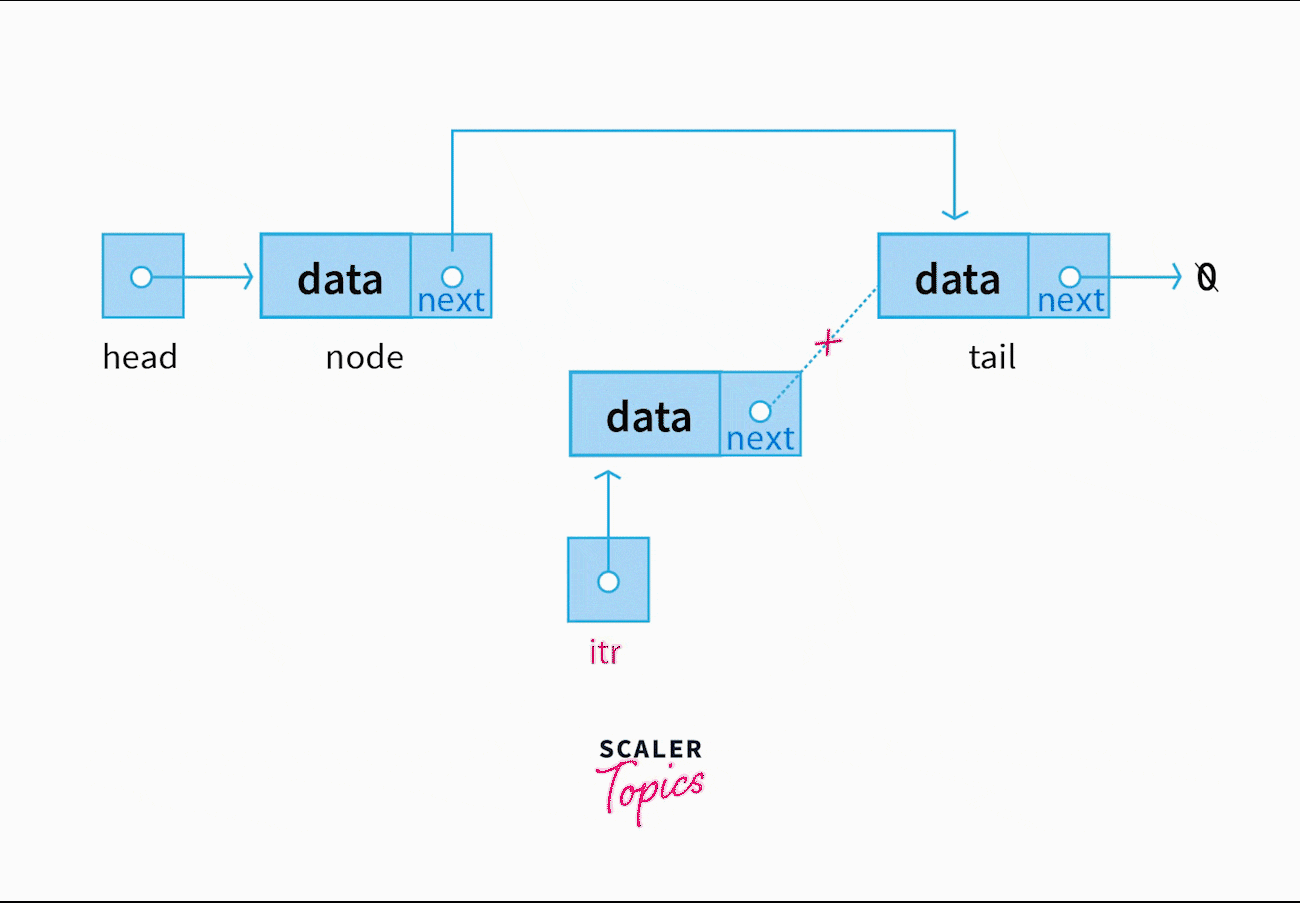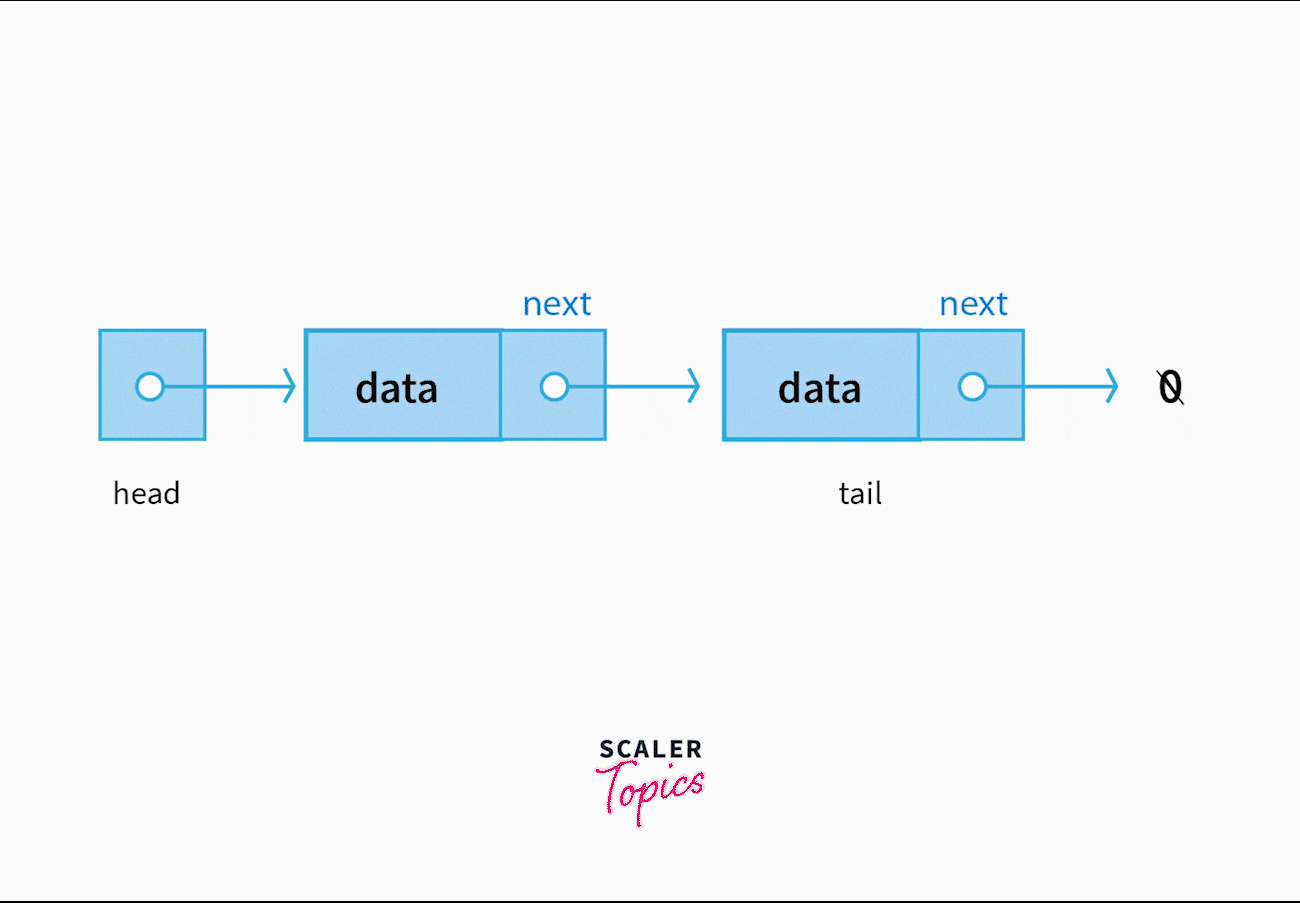
Deletion
We can delete a node located at a specified index by manipulating at most 2 next pointers like so;
consider two pointers, prevNode, and targetNode
set prevNode's next pointer to the targetNode's next pointer and set targetNode's next pointer to NULL
where prevNode denotes a pointer to the node after which targetNode is to be deleted. Following the same reasoning as insertion, the best case and the worst case time complexity stands at Ω(1) and O(n) respectively.
Again just like insertion, the order is important. It's important to realize that setting targetNode's next pointer to NULL as the first step would cost us the reference to the remaining of the linked list (if the targetNode wasn't the Tail).
Search
Given a particular key (data), we need to search for a node whose data matches the key. In the best-case scenario, the head would be the node we are looking for, whereas in the worst-case the required node would be the tail. In terms of time complexity the best case, the average case, and the worst case of searching are denoted as Ω(1), Θ(n), and O(n) respectively.
Implementation of Linked List in C++
Implementation of Linked List in Java
Implementation of Linked List in Python
Time Complexity of Linked List
As you can clearly see that few linked list operations are more efficient than others. To understand, let's observe the dichotomy of linked lists and arrays in the context of time complexity for the aforementioned operations.

And that's why a linked list is not superior to an array or vice-versa. These data structures complement each other and shine in certain use-cases.
To drive the point home, let's look at some of the advantages and disadvantages of a linked list.
Advantages of Linked List
-
Dynamic in nature - Linked lists are dynamic in nature, and their size can be adjusted according to our requirements.
-
Ease of Insertion and Deletion - Insertion and deletion of a node in a linked list remain efficient as the nodes are stored in random locations, and we only need to update the next pointer of a constant number of nodes.
-
Memory efficient - Memory consumption of a linked list is efficient as its size can grow or shrink dynamically according to our requirements.
-
Implementation - Various advanced data structures can be implemented using a linked list vis-a-vis stack, queue, graph, hash maps, etc.
Disadvantages of Linked List
-
Memory usage - A node in a linked list occupies more memory than an element in an array as each node occupies at least two kinds of variables.
-
Accessing a node - If you want to access a node in a linked list, you have to traverse starting from the head. We cannot access any random nodes directly except for the head itself, since nodes don't share a linear order in the physical memory and are only referenced by pointers.
-
Traversing in reverse order - Traversing in reverse order is difficult. Although a doubly-linked list makes it easier but requires more memory to store those extra 'prev' pointers.
Applications of Linked List
It would have been futile if a linked list didn't have many applications beyond a mere movie theater use-case.
Here are some of the applications of a linked list:
-
Linear data structures such as stack, queue, and non-linear data structures such as hash maps, graphs can be implemented using linked lists.
-
Doubly linked lists are useful for building a forward-backward navigation button in a web browser or undo-redo feature in an editor.
-
Circular Doubly linked lists can also be used for the implementation of advanced data structures like Fibonacci Heap.
Conclusion
We have witnessed the necessity, time complexity, applicability of linked lists. We talked about various advantages, disadvantages, and tradeoffs for choosing a linked list over an array or vice-versa.
To wrap it all up, let me recount you the TLDR;
- A linked list is a linear data structure comprising nodes chained together, but those nodes may not be allocated sequentially in the memory.
- This randomness of the distribution of nodes in physical memory holds no constraint as to how big the linked list can be.
- No limitation in size also leads to efficient allocation as long as there are empty spaces.
- Such a linked list supports operations like traversal, insertion, deletion, searching to name a few.
- The traversal and searching drive the time complexity to O(n) whereas insertion and deletion at the beginning lead to Ω(1).
- However, the insertion and deletion at any specified position would be O(n).
- Different kinds of linked lists such as singly, doubly, and circular can be used to implement more advanced data structures as well.
- A linked list is one of the most fundamental and popular data structures next to the array. It has implementations in every programming language like C, C++, Java, Python, and C#.
To get comfortable with this particular data structure as well as in pointers, you got to reverse a linked list along with the following problems:
