Long Division Method to Find Square Root

Code Implementation

Approach

Let us understand the approach with steps and examples. Let us say my N = 10609

Step 1: Divide the Number into segments

• Divide the given number (N) into pairs of digits, starting from the rightmost digit.
• If the number of digits is odd, don't pair the first digit
• In our case, the segments will be: [1,06,09]

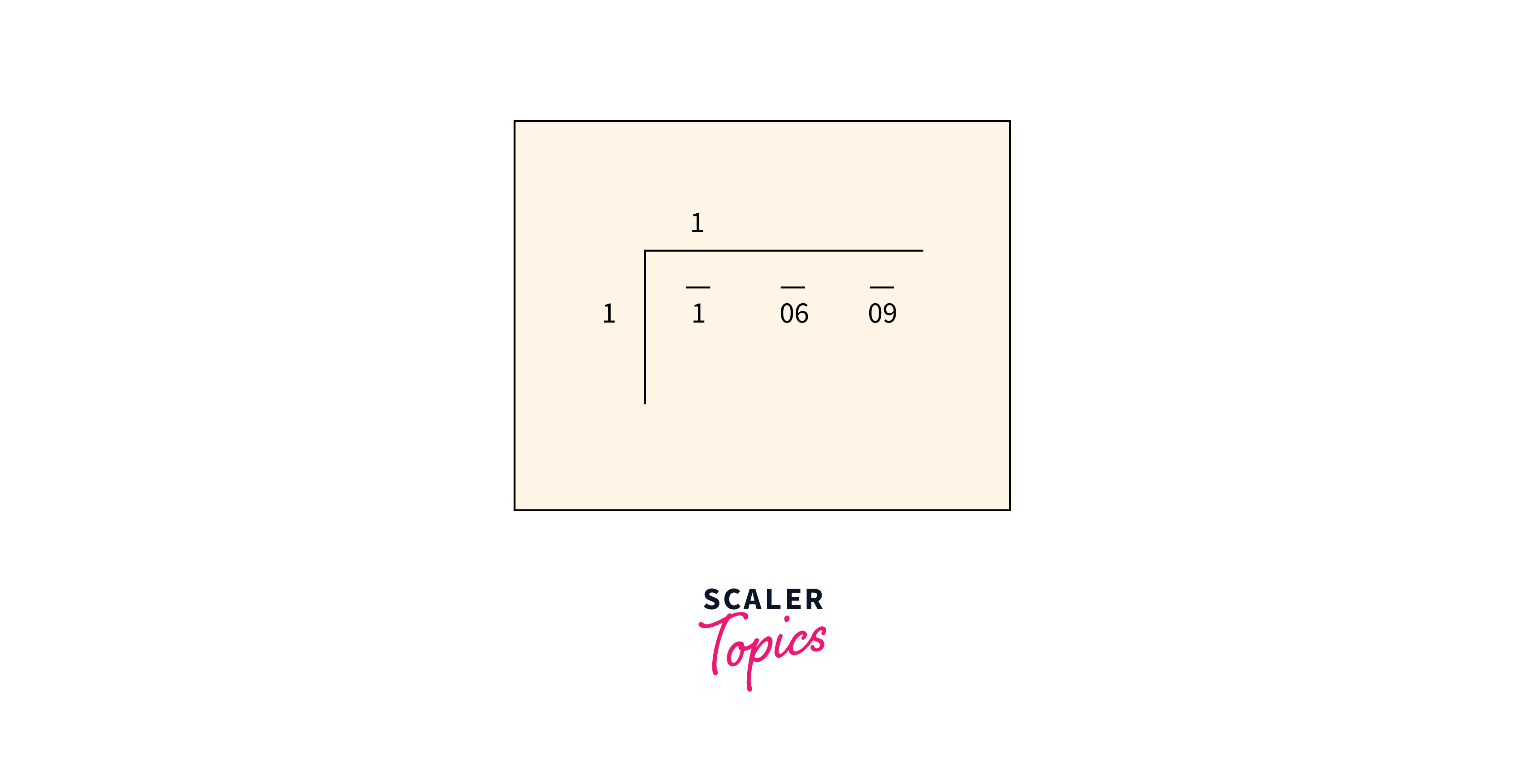
Step 2: Find the Largest Divisor:

• For each segment (dividend), find the largest number (divisor) whose square is less than or equal to the segment.
• Write the divisor as the quotient digit.

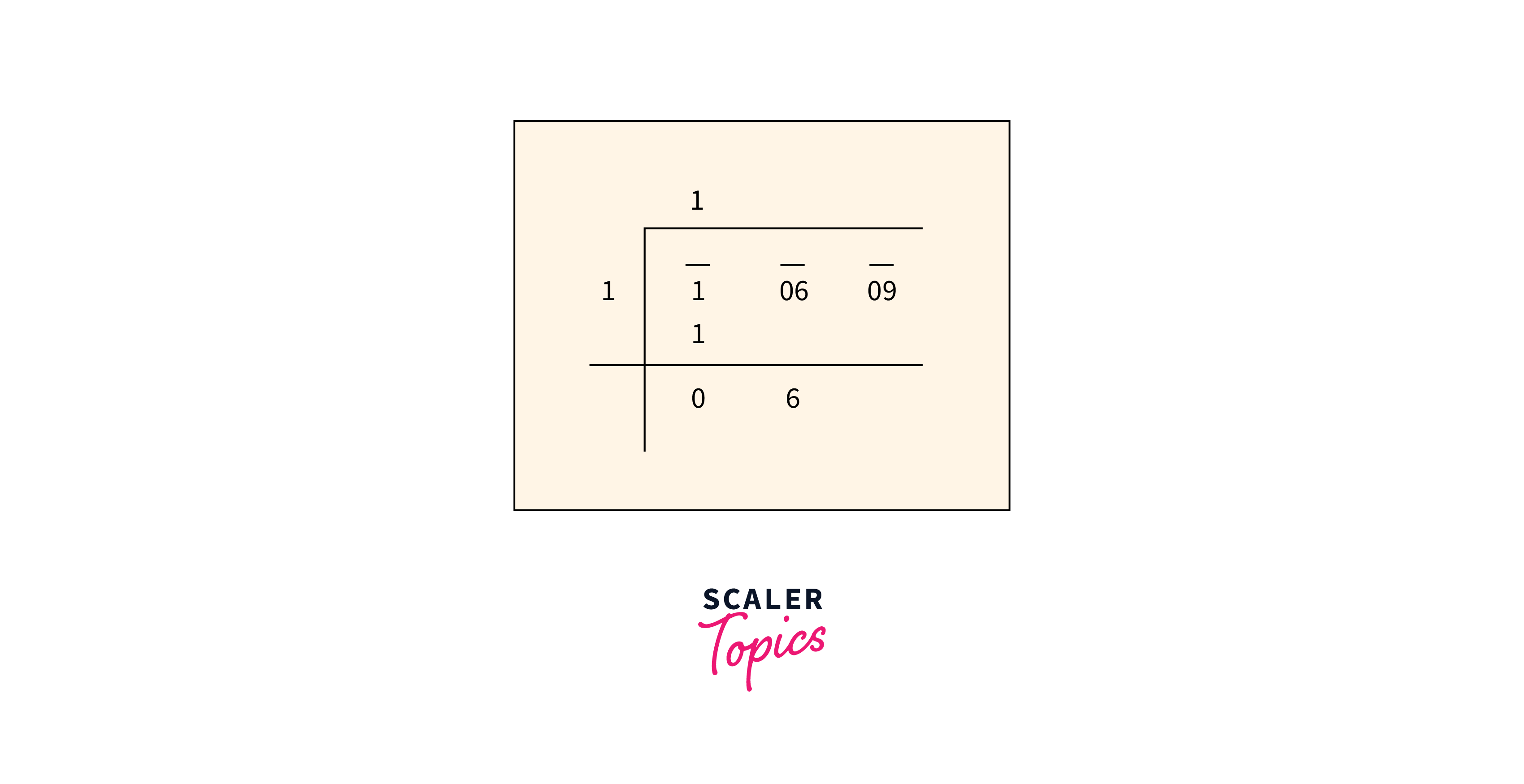
Step 3: Subtract and Update

• Subtract the square of the divisor from the dividend.
• Bring down the next segment (if any) and combine it with the remainder to form a new dividend.

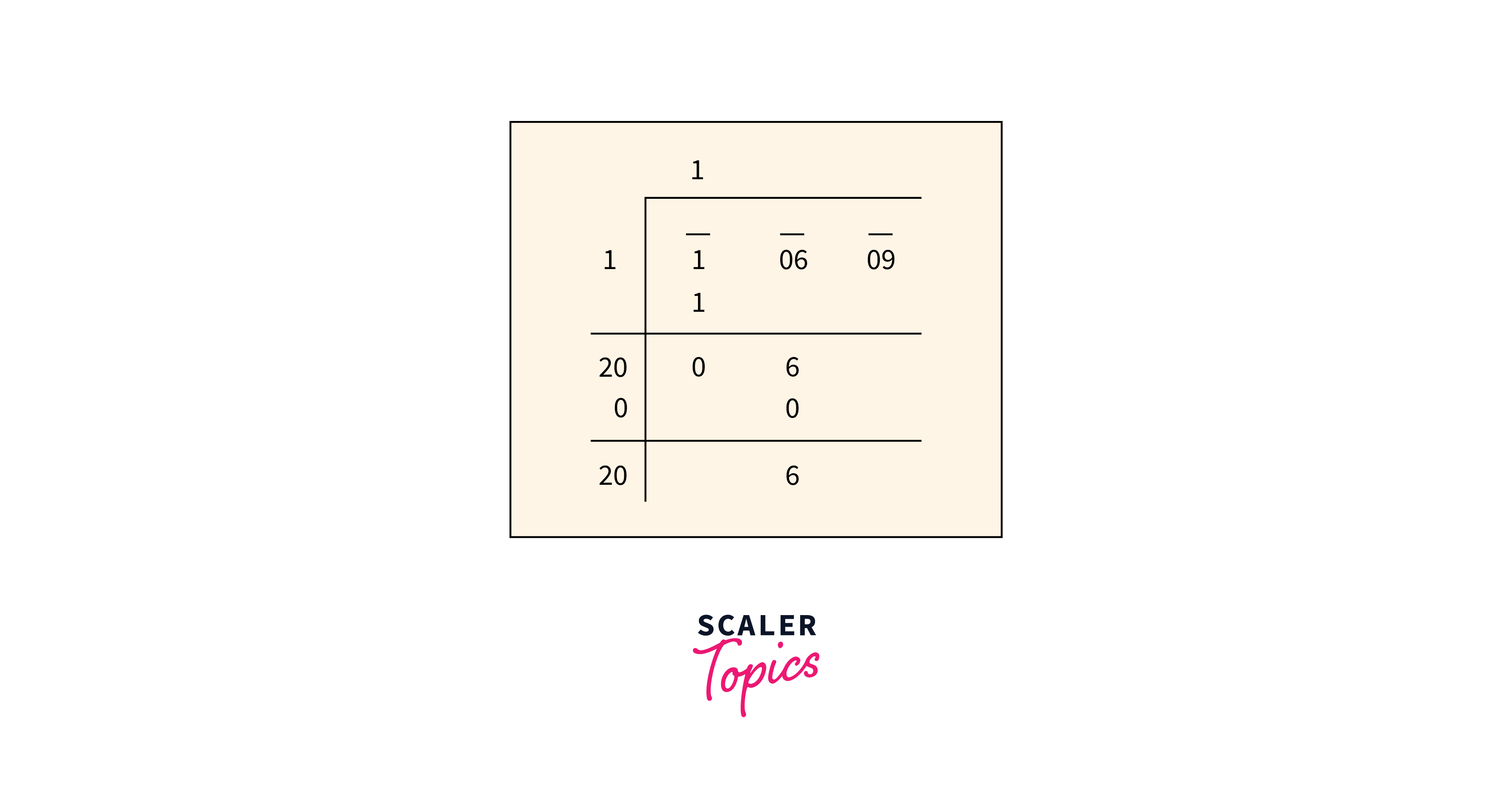
Step 4: Update the Divisor

• Double the existing quotient (initially 0) and add it to itself to form the new divisor for the next segment.
• Choose a suitable digit to concatenate with the doubled quotient, forming the new divisor.
• This digit should be chosen so that the product of the new divisor and the digit is equal to, or less than, the current dividend.
• Append the chosen digit to the doubled quotient, forming the new divisor.
• Use this new divisor for the next iteration of step 2.

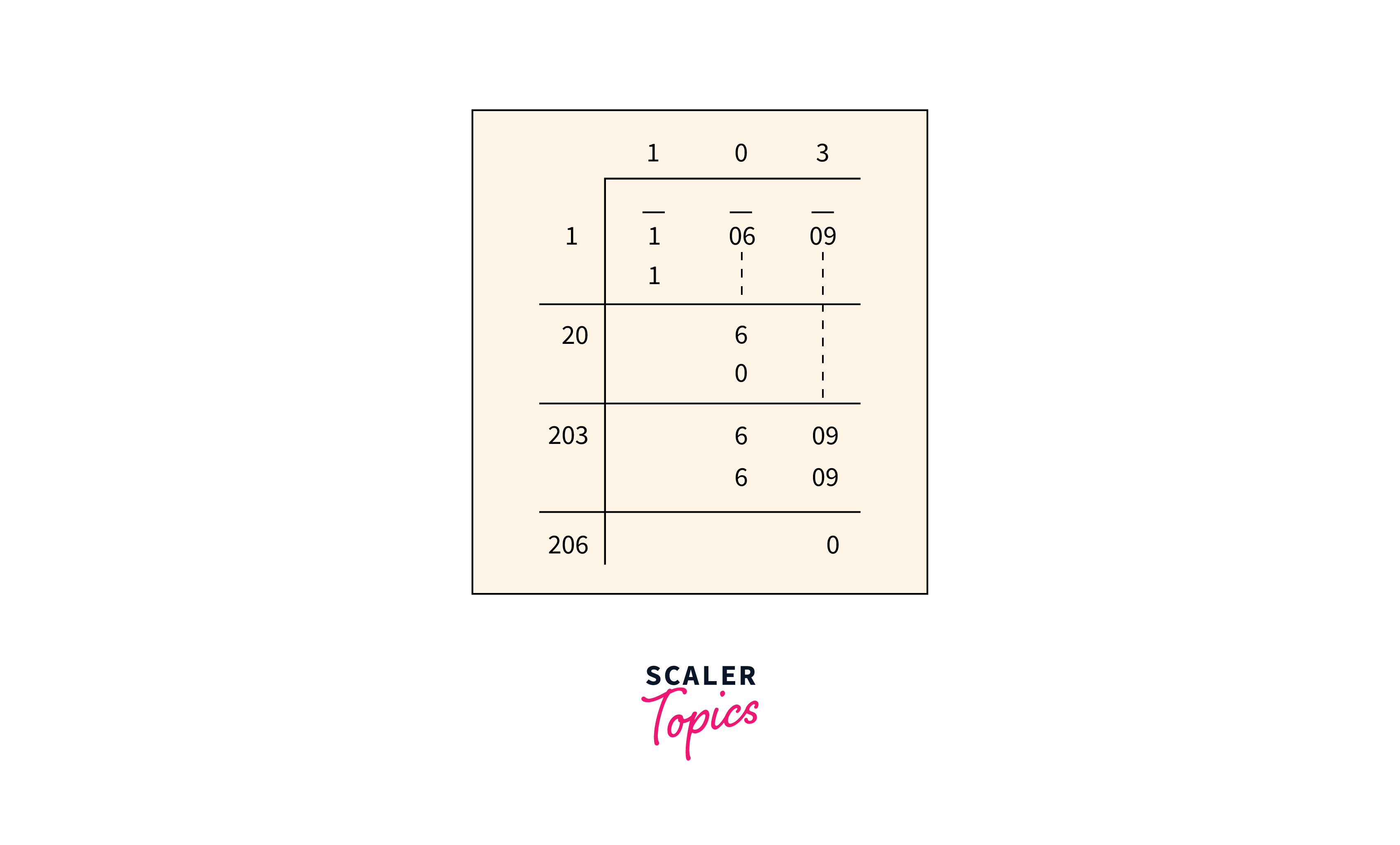
Step 5: Repeat

• Repeat steps 2, 3, and 4 for each remaining segment.
• The final quotient obtained after finishing all segments is the approximate square root of the given number (N).

The code for the above method is as follows:

Java

C++

Python

JavaScript

Output:

Explanation:

• The procedure is similar to the mathematical method. We first divide the number into segments.
• Then we iteratively loop through each segment.
• Now we loop through all digits from 0 to 9 and update the quotient, dividend, and divisor.
• The code initializes currentRemainder to a large value (INFINITY) and iterates through each digit (0 to 9) to check for the perfect square closest to each segment.
• There are other approaches to finding the square root of the number, we can use binary search to find the approximate square root, and we can also use in-built math classes in programming languages to find the square root of the number.
• The main aim of using the long division method to find the square root of the number is to be able to convert mathematical procedures into code. It is important to be able to perform every task that we can do on pen paper to be able to perform it using code in at least any one programming language.

Dry Run of the sqrtByLongDivision Function:

Input: 100

Step 1: Preprocessing:

• segmentIndex, currentDivisor, unitsDigitOfQuotient, currentQuotient, currentDividend, currentRemainder are set to 0, and segments is a new array of size 10.
• unitsDigit, and segmentIterator are loop counters and are not initialized.

Step 2: Splitting the number into segments:

• Iteration 1:
  • number is 100, so segments[0] is assigned 0 (last two digits), and number becomes 1 (after removing the last two digits). The segmentIndex = 1.
• Iteration 2:
  • number is 1, so segments[1] is assigned 1 (initial digit), and number becomes 0 (after removing the last two digits). The segmentIndex = 2. And the iteration terminates.

Step 3: Long division loop:

• segmentIndex-- i.e. segmentIndex = 1
• segmentIterator is 1.
• Inner loop (finding the perfect square digit):

  • currentRemainder is initialized to INFINITY.

  • currentDividend is updated to 1.

  • unitsDigit is 0 initially.

  • For each unitDigit:

    • unitDigit = 0
    • currentRemainder is calculated as currentDividend - (currentDivisor * 10 + unitsDigit)*unitsDigit = 1;
    • If currentRemainder is non-negative and less than the previous currentRemainder (closest to perfect square), unitsDigitOfQuotient is updated to the current unitsDigit i.e. 0.
    • unitDigit = 1
    • currentRemainder is 1.
    • currentDividend is 1.
    • The condiiton currentRemainder >= currentDividend - ((currentDivisor * 10 + unitsDigit) * unitsDigit) && currentDividend - ((currentDivisor * 10 + unitsDigit) * unitsDigit)>= 0 is true.
    • currentRemainder is calculated as currentDividend - (currentDivisor * 10 + unitsDigit)*unitsDigit = 0;
    • If currentRemainder is non-negative and less than the previous currentRemainder (closest to perfect square), unitsDigitOfQuotient is updated to the current unitsDigit i.e. 1.
    • For the next loops the if condition of the inner loop will not be true as currentRemainder = 0.
• After the inner loop, currentQuotient is updated to currentQuotient * 10 + unitsDigitOfQuotient = 1.
• currentDivisor is updated to currentQuotient * 2 = 2.
• currentDividend = currentRemainder = 0.
• segmentIterator decreases to 0.

Step 4: Next iteration of the long division loop:

• segmentIterator is 0.
• Inner loop (finding the perfect square digit):

  • currentRemainder is initialized to INFINITY.

  • currentDividend is 0 and is updated to 0 as segments[segmentIterator] is 0.

  • unitsDigit is incremented from 0 initially.

  • For each unitDigit:

    • unitDigit = 0
    • currentRemainder is calculated as currentDividend - (currentDivisor * 10 + unitsDigit)*unitsDigit = 0;
    • If currentRemainder is non-negative and less than the previous currentRemainder (closest to perfect square), unitsDigitOfQuotient is updated to the current unitsDigit i.e. 0.
    • For the next loops the if condition of the inner loop will not be true as currentRemainder = 0.
• After the inner loop, currentQuotient is updated to currentQuotient * 10 + unitsDigitOfQuotient = 10.
• currentDivisor is updated to currentQuotient * 2 = 20.
• currentDividend = currentRemainder = 0.
• segmentIterator decreases to -1.

Step 5: Next iteration of the long division loop:

• segmentIterator is -1.
• no more segments are remaining, so the loop exits.

Step 5: Return result:

• currentQuotient = 10 is returned as the square root of the input number.

Output:

Time and Space Complexity

Time Complexity: O((log100n)^2 * 10) It's quadratic in the number of bits of the numbers we're dividing, which means that to divide n by m you need O((log max(m,n))^2) time. This is because each subtraction takes O(log max(m, n)) time. Here our m is 100 so the time complexity is O((log100n)^2 * 10).

Auxiliary Space: O(1) As we are not using any additional space the space complexity is O(1).