LRU Cache Implementation

Problem Statement

Design a data structure to implement following the operations of Least Recently Used (LRU) Cache -

• LRUCache (capacity) - To initialize LRU cache with its size being capacity.
• put (key, value) - Add the key-value pair in the cache, and if the cache already contains an entry with its key being key update its value to value. If the size of the cache exceeds its capacity, remove the least recently used key-value pair from the cache.
• get (key) - Return the value associated with the key, if the cache does not contain an entry with its key being key return a default value (say -1).

Note - The compulsion here is that, you need to implement such that both the put and the get operation take $O(1)$ time on an average.

LRU Cache

Before beginning with the LRU Cache, let's see what does a cache means? We know that we store all the data on hard disks/SSDs but there are some data items that we access too frequently and accessing them again and again from a hard disk is too time-consuming. Hence, we prefer to store them in a much faster storage type so that they can be accessed instantly. Since the fast storage types are very costly therefore we can only have a limited fast storage type and we term it Cache (pronounced as "cash" 💵) Memory or simply Cache.

LRU (Least Recently Used) cache is one of the most popular caching strategies. It defines the policy to remove elements from the cache to make space for the new elements, once the size of the cache exceeds its capacity. As the name suggests, we will remove the element that was least recently used.

Structure of LRU Cache

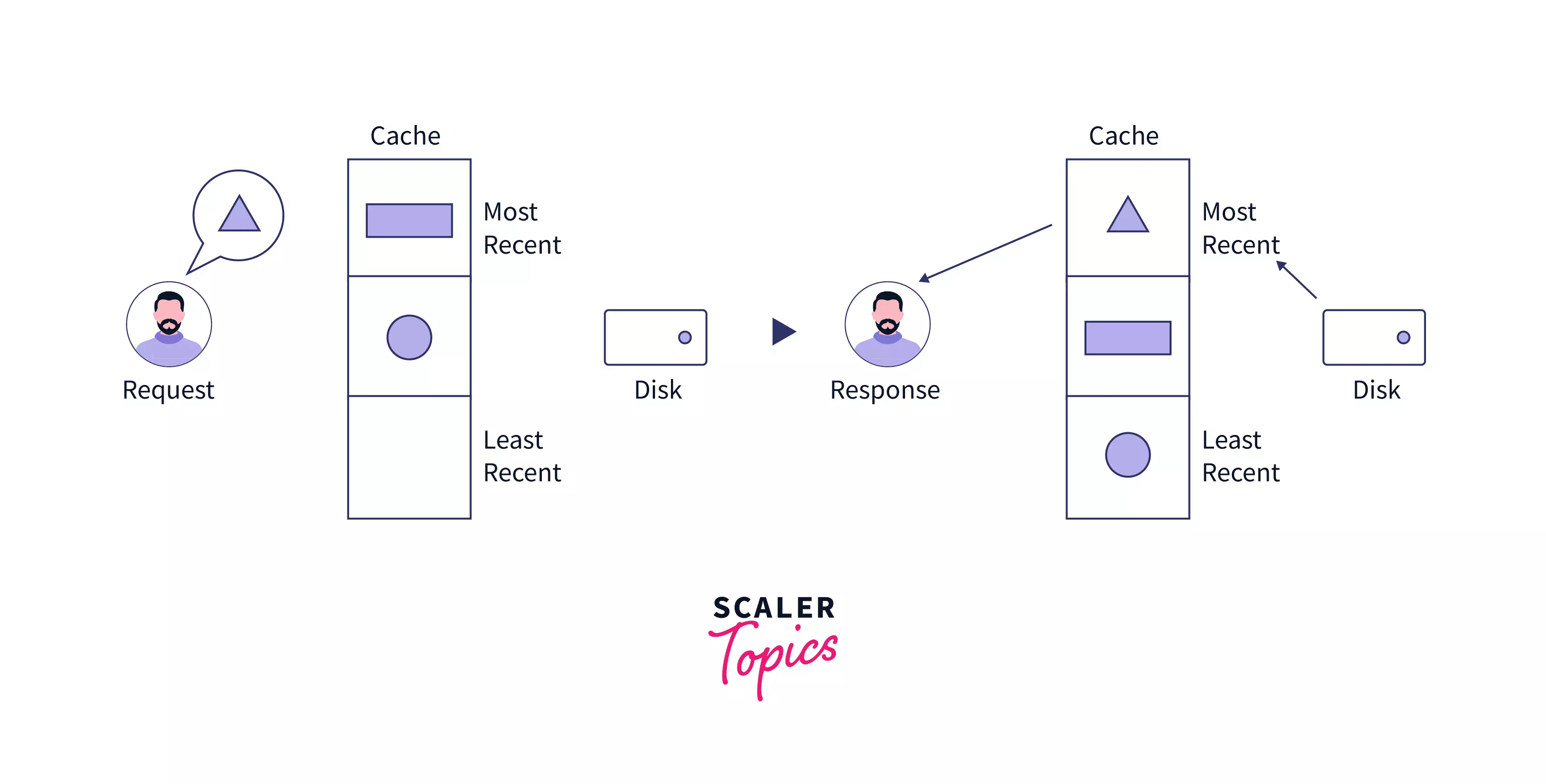As it can be seen in the image given above, LRU Cache is like a series of memory blocks that contains some data. Initially, the cache holds two data elements in it, and then the user requests a data that is not present in the cache, hence it will be fetched from the disk and returned to the user, but due to this process, the fetched data item becomes the most recently used hence it is placed at the top of the cache. Now if the user requests any of the data items that are present in the cache, instead of fetching it from the disk, it will be instantly returned to the user.

Example of LRU Cache

Let's say initially you have $n$ number of books on your study table arranged in one upon another fashion. Every day you read a random book and after reading it you put it on the top. Let's say this process continues for a week, now for the sake of cleanliness, you decide to put back 1 book from your study table to the bookshelf. Which one you will be going to put back depends on how you remove that 1 excess book that is there on your table. If you follow the LRU strategy, you will end up removing the bottom-most book as it is the least recently used by you.

Now let's see how the LRU cache works in the software terms - Let's say we have a cache of capacity $3$ $i.e.$ it cannot hold more than three Key-Value pairs. And we need to perform the following operation on it (in the given order) -

• put - 1, 1
• put - 2, 2
• put - 3, 3
• get - 2
• get - 1
• put - 4, 4
• get - 1
• get - 2
• put - 5, 5
• get - 3

The output of the above-given series of operations is 2, 1, 1, 2, -1. Note that put operations do not produce any output, only the get operation produces an output.

Let's see how this output comes Let's say the cache is represented as a two-column table where the entry which is at the top is most recently used, and the ones which are at the bottom are the least recently used.

• Initially, our hash is empty.

• After the operation put - 1, 1, our has will look like -

  Key	Value
  1	1

• Similarly after the operations put - 2, 2 and put - 3, 3 we will have -

  Key	Value
  3	3
  2	2
  1	1

• Now, we perform the operation get - 2, and it will print 2 as output because we have value 2 associated with the key 2. And since entry with key as 2 has been accessed it is now the most recently used Key-Value Pair. So we will have -

  Key	Value
  2	2
  3	3
  1	1

• Now, we perform the operation get - 1, it will print 1 as output because we have Value 1 associated with the key 1. And since the entry with key as 1 has been accessed it is now the most recently used Key-Value Pair. So we will have -

  Key	Value
  1	1
  2	2
  3	3

• Now, we perform the operation put - 4, 4, we will add to in the cache and since now cache size exceeds its capacity we will remove the least recently used Key-Value pair.

  Key	Value
  4	4
  1	1
  2	2

• Similarly, we will perform the remaining steps, and just before performing the last operation our cache will look like -

  Key	Value
  5	5
  2	2
  1	1

  Now we need to perform the last operation $i.e.$ get - 3, which will print -1 as the output because there is no entry with key as 3 in the cache.

Operations in LRU Cache

We have two operations in the LRU Cache -

1. put (key, value) - In this operation, we put a new entry in our cache. And if the cache size is full we evict the entry following the LRU strategy.
2. get(key) - This operation returns the value associated with the key if the cache contains an entry with its key being key, otherwise it returns a default value.

Data Structure used to implement LRU Cache

We use two data structures for LRU Cache implementation so that both the put and the get operation can be executed in constant time.

Queue

We use a queue (implemented using a Doubly linked list) to store Key-Value pairs, as we are following the LRU strategy we prefer keeping the most recently used Key-Value pair at the front and the least recently used pair at the end. Doubly Linked List is chosen because adding/removing elements from the doubly linked list from any position takes $O(1)$ time in the worst case.

HashMap

We will also use a Hash Map to map the keys with the corresponding nodes present in the cache. This will help to access any node of cache in $O(1)$ time even in the worst case.

Implementation

As discussed in the previous section, the queue data structure is used for LRU Cache implementation. Here we will use a doubly-linked list to represent a queue. And for the hashing part, we will use the Map/Dictionary available in STL/Collections of almost all the major programming languages.

The idea is to store all the Key-Value pairs in the form of nodes of a doubly-linked list arranged in a sequential manner so that adding/removing a Key-Value pair can take place in $O(1)$ time. Also, we will store the Key-Node pairs in the 'Map' that maps the key with its associated node, so that we can access any node in $O(1)$ time.

Put Operation

The implementation of the put operation is as follows -

• Let's say we are asked to add a(key, value) pair in the cache.
• The first step would be to check if the cache already has a node with its Key being key.
• If such node already exists do the following:
  • Update node's value to value.
  • Move it to the head of the List, because while updating the value we have accessed it, due to which it becomes the most recently used Key-value pair.
• Otherwise do the following:
  • Define a new node with given values of key and value (let it be newNode).
  • Add it to the head of the list.
  • Add it to the Map.
  • If after adding newNode size of the list exceeds the capacity of cache, do the following:
    • Remove node present at the tail of the List (since it is the least recently used Key-Value pair).
    • Remove it from the map.

Get Operation

The implementation of the get operation is as follows -

• Let's say we need to find the value of a node with its Key being key.
• We will check if the map contains any node with the corresponding key.
• If such node does not exist, return the default value $-1$.
• Otherwise, move the node to the head of the list, this is because while performing the get operation they have been accessed due to which they are the most recently used Key-Value pair.

Dry Run (Visualizing the LRU Cache)

While writing the code, we will define a Node class to implement a doubly linked list which will contain the address of the next and previous pointer, it also contains the key and value associated with this node.

To make all the operations a bit simple, we will declare two dummy nodes to mark the head and the tail of the list (let their name be head and tail). Also, we will initialize our HashMap. Initially, our cache will look like this-

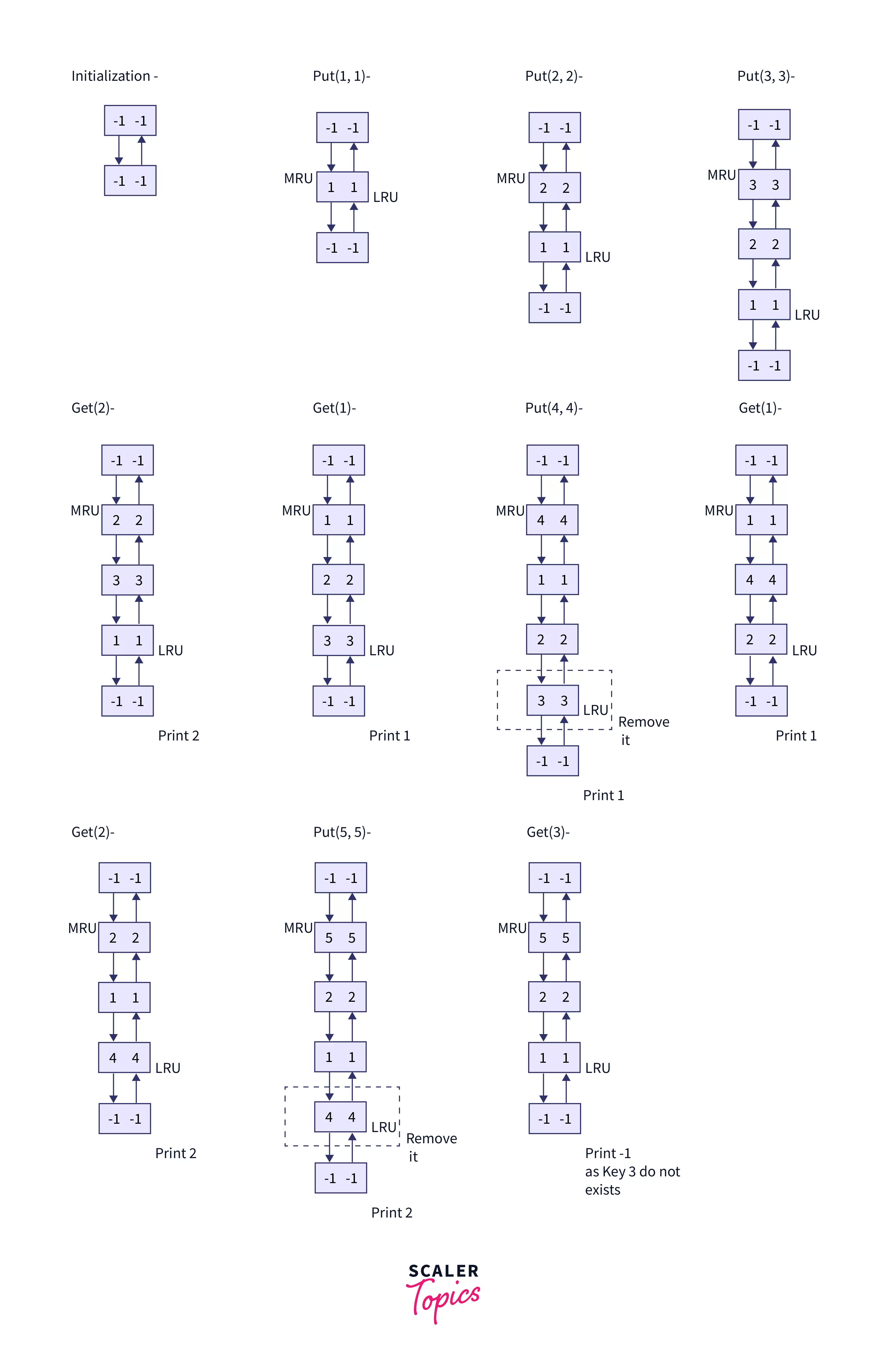
Now we will perform the following operations on it -

• Put(1, 1)
• Put(2, 2)
• Put(3, 3)
• Get(2)
• Get(1)
• Put(4, 4)
• Get(1)
• Get(2)
• Put(5, 5)
• Get(3)

Java Implementation

Output: -

C++ Implementation

Output: -

Python Implementation

Output: -

Complexity Analysis

• Time Complexity -
  • Put operation - All the statements (adding a node in the list and removing a node from the list) in the put operation take constant time, and hence the overall time complexity is $O(1)$.
  • Get Operation - Also, in the get operation, all the statements (accessing a node from the map and moving a node of the list to its head) can be executed in a constant amount of time which makes the time complexity to be $O(1)$.
• Space Complexity - Since we are using a doubly-linked list and a map whose size can reach up to $n$, where $n$ is the size of the cache. Therefore, the overall space complexity is $O(n)$.