Matrix Multiplication in C++

Introduction

A matrix is a rectangular array of numbers that are arranged in the form of rows and columns. In C++, a matrix is a so-called 2D array, with the dimensions as m,n, where m represents the number of rows present in the array, and n represents the number of columns in the array.

There are a few points to remember before the multiplication of the 2 matrices.

1. If matrix M1 with the shape of (m,n) and matrix M2 with the shape of (p,q), then for multiplication of M1 and M2, it is mandatory that n must be equal to p.
2. After calculating the multiplication of M1 and M2, the resultant matrix M3 will have a shape of (m,q).

The above 2 points must keep in mind during the matrix multiplication.

Before getting into the idea of calculating the matrix, let's recall how we have calculated the matrix in mathematics on paper.

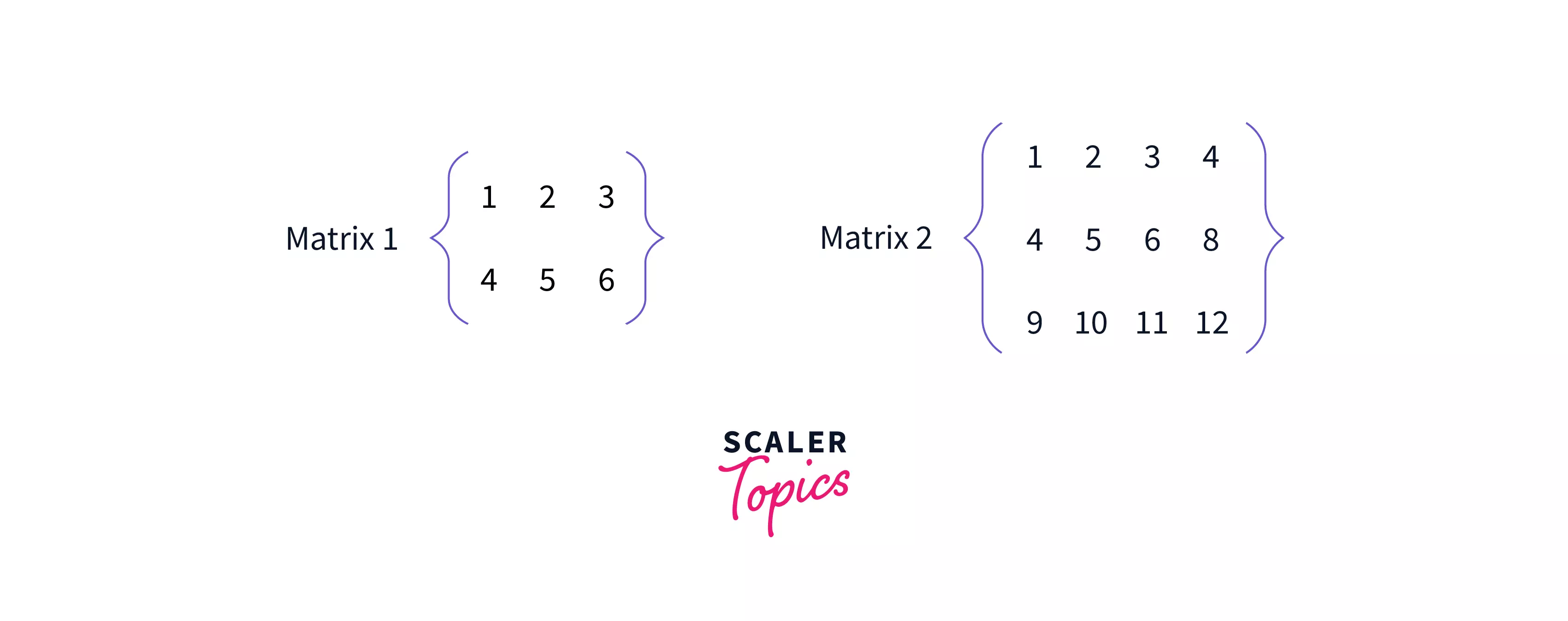
Suppose we have two matrices, M1 and M2, with shapes (2,3) and (3,4).

From the above 2 points, we can conclude that the (n=3) and (p=3) are equal, so matrix multiplication is valid. Now, we can also conclude the shape of the resultant matrix, i.e., M3 will be (2,4).

Let M1 =

M2 =

Now, we have to declare both the matrix and make assumptions using above mentioned two points. Now, we will multiply M1 and M2 to get our M3.

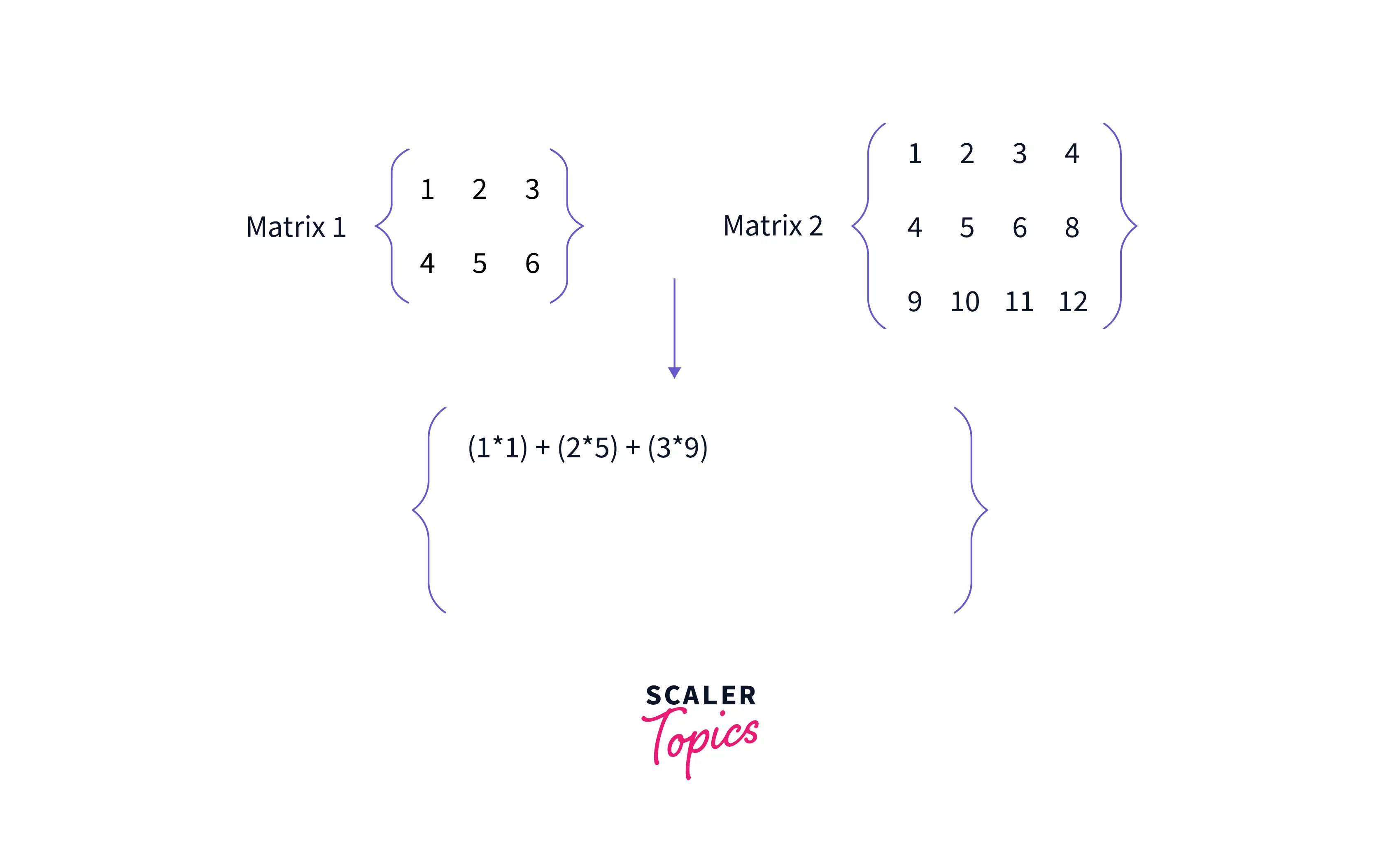
1. For every row in M1 and every column in M2. Multiply each element of the row of M1 with the column of M2, and add the elements.

First row of M1 is [1,2,3], and first column of M2 is [1,5,9]. Multiply each element with each other, so the resultant will be [1 * 1, 2 * 5, 3 * 9], and now add all the three elements, i.e., to form a single element. This resultant element will be the first element of our resultant M3 matrix. [(1 * 1) + (2 * 5) + (3 * 9)] = [1+ 10 + 27] => 38.

We will continue this process till we cover all the rows with all the columns.

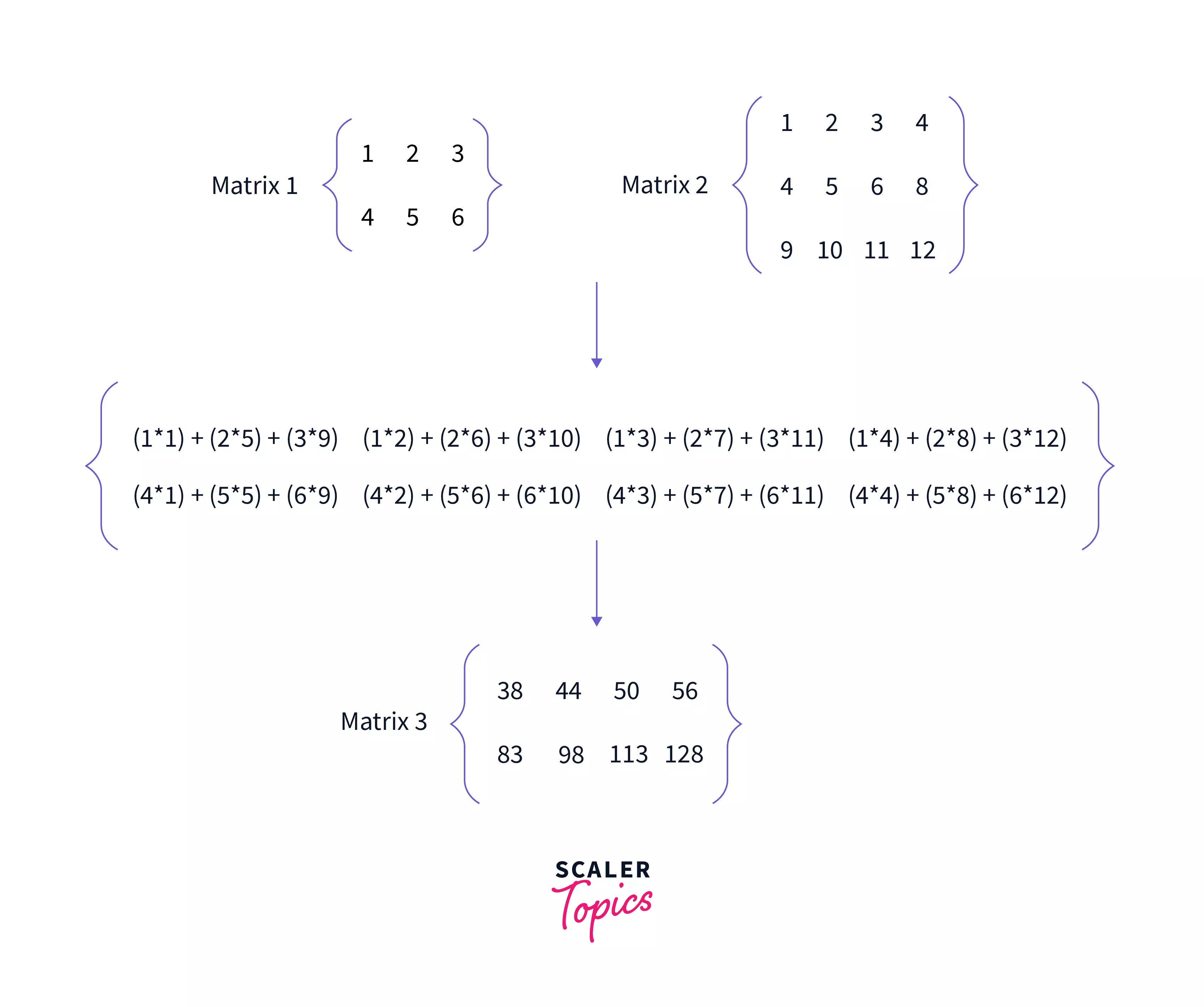
We have continued our process till we haven't covered all the rows in M1 and all the columns in M2. Now, we can see that the shape of matrix M3 is (2,4). Hence our above two mentioned points come up to be true.

The above case is what we have done in mathematics. But in this article, we have to write the code to multiply two matrices. The process of writing code is also the same. We will follow the same steps in writing code also.

C++ Program for Multiplication of Square Matrices

Let us consider that we have a 2 square matrix, i.e., with the number of rows equal to the number of columns.

Input:

In the above code, we have created two matrices, matrix1 with shape (3,3) and matrix2 with shape (3,3).

CODE TO MULTIPLY 2 SQUARE MATRICES.

Output:

Time Complexity: $O(n^3)$ The Time Complexity of the multiplication of Square Matrices is $O(n^3)$ because we use 3 for loops that continue for all rows and columns, i.e., N. So, its complexity will be $O(n^3)$.

Auxiliary Space: $O(n^2)$ We store a 2D array for the resultant matrix, which takes $O(n^2)$ auxiliary space.

C++ Program for Multiplication of Rectangular Matrices

Let us consider that we have two rectangular matrices, i.e., with the number of columns of matrix1 equal to the number of rows of matrix2.

Input:

CODE TO MULTIPLY 2 RECTANGULAR MATRICES

Output:

In the case of a Rectangular matrix, we will have Time Complexity as O(m * n * q) or O(m * p * q).

Auxilliary Space: O(m * q) because our new matrix m3 is of size (m, q), m rows, and q columns, so it requires m * q space.