Maximum Subarray Sum
FREE
Problem Statement
We are given an array A of size N which consists of both positive and negative integers. We have to write a program to find the Maximum Sum of Subarray.
Note: A subarray is a contiguous part of an Array.
Example
Input: [2,-3,6,-5,4,2]
Output: 7
Explanation: The subarray [6,-5,4,2] is the max sum contiguous subarray with sum 7.
Input: [-2, 5, -2, 3]
Output: 6
Explanation: The Subarray [5, -2, 3] is the max sum contiguous subarray with sum 6.
Constraints
What is a Subarray?
A subarray is a continuous part of the array which can be made by deleting zero or more elements from the beginning or can be made by deleting zero or more elements from the end or both sides.
Example:
Array: [1,3,5,6,2] Example of some subarrays: [1,3,5], [5,6,2], [3,5,6,2], [1], [1,3,5,6,2]
Build an AI-First Career, Master the Complete Skillset
Choose from our industry-leading programs designed for career success
Modern Software and AI Engineering Program
Master full-stack development with AI integration
+1000 moreModern Data Science and ML with specialisation in AI
Advanced data science techniques with AI specialization
+1000 moreAdvanced AIML with Specialisation in Agentic AI
Deep dive into AIML with focus on Agentic systems
+1000 moreDevOps, Cloud & AI Platform Engineering
Build and manage AI-powered cloud infrastructure
+1000 moreAI Engineering Advanced Certification by IIT-Roorkee
Premier AI engineering certification from IIT-Roorkee
AI Forward Deployed Engineer Program
Full-stack engineering, production AI and client-facing consulting
+1000 moreApproach 1: Brute Force Approach Using 3 Nested Loops
Algorithm:
- Run a loop from i=0 to i=n-1
- Run a nested loop inside the first loop from j=i to j=n-1
- Run another nested loop inside the second loop from k=i to k=j
- For each subarray calculate the currSum and finally maintain a variable (say maxSum) and each time the innermost loop and we will update the answer by maxSum = max(maxSum,currSum)
C++ Implementation
Java Implementation
Python Implementation
Complexity Analysis
Time Complexity Analysis
We can see that we are using 3 Nested Loops
- 1st loop will always run from 0 to n-1 i.e. N times
- In the worst case 2nd loop will run from 0 to n-1 i.e. N times because when i=0, j will run from 0 to n-1.
- In the worst case 3rd loop will run from 0 to n-1 i.e. N times because when i=0 and j=n-1, k will run from 0 to n-1
So the worst-case time complexity of this approach becomes O(N * N * N) i.e. O(N^3)
Space Complexity Analysis
We are only declaring variables that we consider as O(1) space, so its overall space complexity is O(1)
Time complexity: O(N^3) Space complexity: O(1)
Approach 2: Using two Nested Loops
Algorithm:
- Run a loop from i=0 to i=n-1
- Run a nested loop inside the first loop from j=i to j=n-1
- For each subarray calculate the currSum and finally maintain a variable (say maxSum) and each time the innermost loop and we will update the answer by maxSum = max(maxSum,currSum)
C++ Implementation
Java Implementation
How Scaler Transformed Careers in Different Fields
Scaler learners achieved 2.5x salary growth with average post-Scaler CTC reaching ₹23L.
Google
Amazon
Microsoft
Flipkart
Adobe1200+ morePython Implementation
Complexity Analysis
Time Complexity Analysis
We can see that we are using 2 nested loops
- 1st loop will always run from 0 to n-1 i.e. N times
- In the worst case 2nd loop will run from 0 to n-1 i.e. N times because when i=0, j will run from 0 to n-1.
So the worst-case time complexity of this approach becomes O(N * N) i.e. O(N^2)
Space Complexity Analysis
We are only declaring variables that we consider as O(1) space, so its overall space complexity is O(1)
Time complexity: O(N^2) Space complexity: O(1)
Approach 3: Using the Divide and Conquer Algorithm
Algorithm:
-
Divide the given array into two halves
-
Initially, our range is from l=0 to h=n-1
-
At each step divide the array using m = (l+h)/2, where m is the middle index and now divide the array into two halves, one from l to m and another from m+1 to h
-
Calculate the following 3 values
- Maximum Subarray Sum of the left half (By making a recursive call)
- Maximum Subarray Sum of the right half (By making a recursive call)
- Maximum Subarray Sum such that this subarray crosses the middle point of the array
-
Return the maximum of the above calculated 3 values
C++ Implementation
Java Implementation
Turn Learning into Career Growth
Python Implementation
Complexity Analysis
Time Complexity Analysis
maximumSubarraySum() is a recursive function in which we are dividing the array into 2 equal parts, and we are calling the maxSumCrossingMiddle() function each time we divide the array, so the Time Complexity is as follows:
- Each time maximumSubarraySum() is divided into 2 equal parts, so the time complexity of dividing the array into two parts, until its size becomes 0 is O(NlogN)
- In the function maxSumCrossingMiddle(), first, i will run from m to l, then i will run from m+1 to h, so in the worst case i can run from 0 to n-1
- So in maxSumCrossingMiddle() the Time Complexity will becon O(N+N) which is equivalent to O(N)
So the worst-case time complexity of this approach becomes O(N * LogN) i.e. O(NLogN)
Space Complexity Analysis
We are only declaring variables that we consider as O(1) space, so its overall space complexity is O(1)
Time complexity: O(N*LogN) Space complexity: O(1)
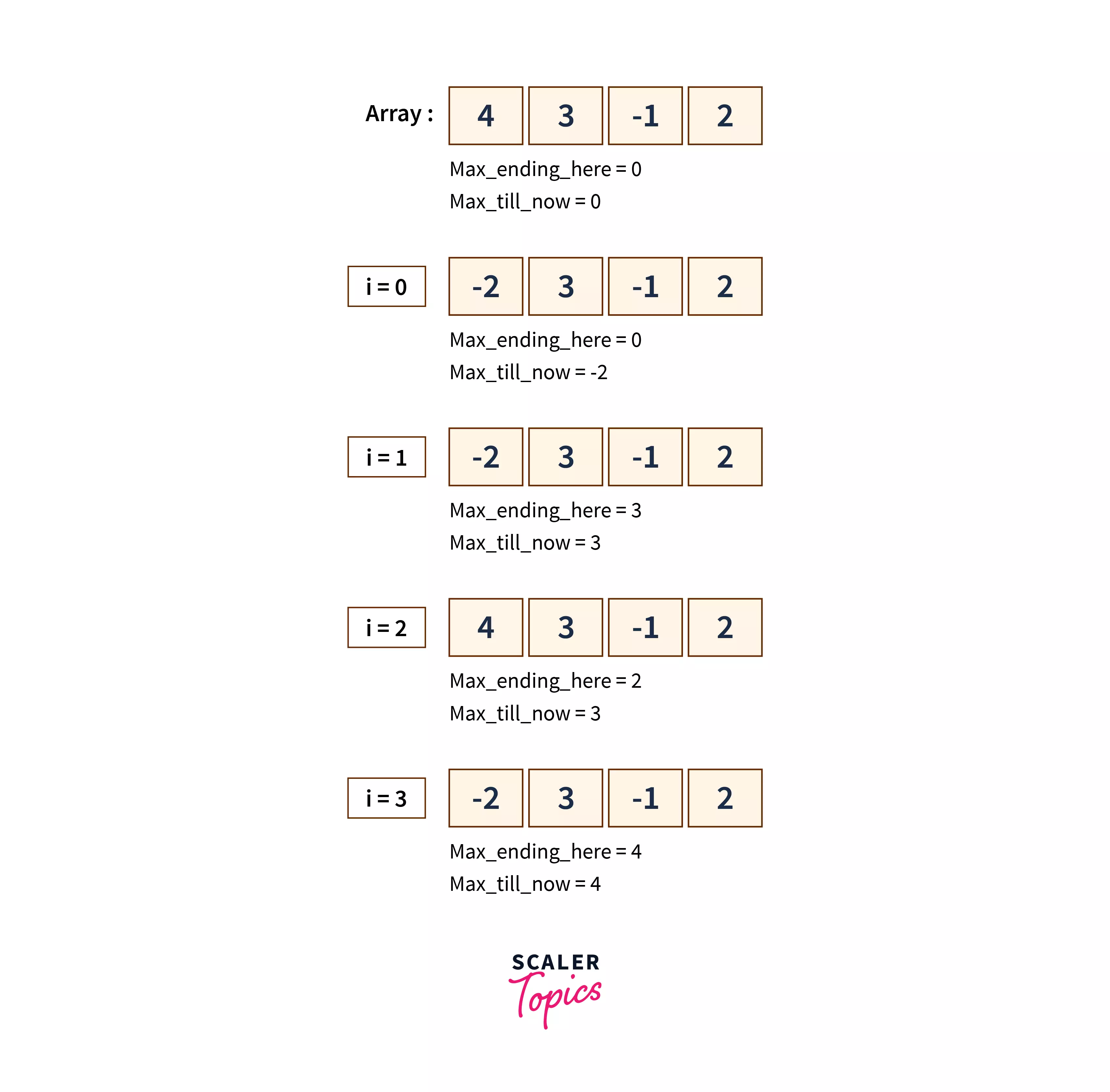
Approach 4: Using Kadane's Algorithm (Dynamic Programming)
Kadane’s Algorithm is a dynamic programming algorithm that can efficiently calculate the maximum subarray sum
Algorithm:
- Initialize a variable named max_till_now=0
- Initialize another variable max_ending_here=0
- Follow the below steps at each index from i=0 to i=n-1
- max_ending_here = max_ending_here + A[i]
- if(max_ending_here>max_till now) max_till_now = max_ending_here
- if(max_ending_here<0) max_ending_here=0
- Return the variable max_till_now
C++ Implementation
Java Implementation
Python Implementation
Complexity Analysis
Time Complexity Analysis
We can see that we are using only 1 loop in this approach.
- The loop will always run from 0 to n-1 i.e. N times
So the worst-case time complexity of this approach becomes O(N)
Space Complexity Analysis
We are only declaring variables that we consider as O(1) space, so its overall space complexity is O(1)
Time complexity: O(N) Space complexity: O(1)
Explaination
Conclusion
In this quick tutorial, we have discussed 4 different methods to find the Maximum Subarray Sum.
- Method 1: Brute force approach using 3 nested loops | Time Commplexity : O(N^3)
- Method 2: Using 2 nested loops | Time Commplexity : O(N^2)
- Method 1: Using Divide and Conquer algorithm | Time Commplexity : O(NLogN)
- Method 1: Kadane's Algorithm (Dynamic Programming) | Time Commplexity : O(N)
- We have reduced the Time Complexity from O(N^3) to all the way O(N)
