n Queen Problem

What is N Queen Problem?

The N-Queen is the problem of placing n queens on a chessboard of dimensions $n\times n$ such that no queen can attack another queen in a single move.

Problem Statement

We need to check if there exists such an arrangement of n queens and if it exists then print the arrangement.

Note that a queen in chess can attack in any of the eight directions i.e. left/right, upward/downward, diagonally upward/downward.

Examples

Example 1 -

Input - 4

Output - . Q . . . . . Q Q . . . . . Q .

Explanation - The arrangement of queens on the chessboard looks like this -

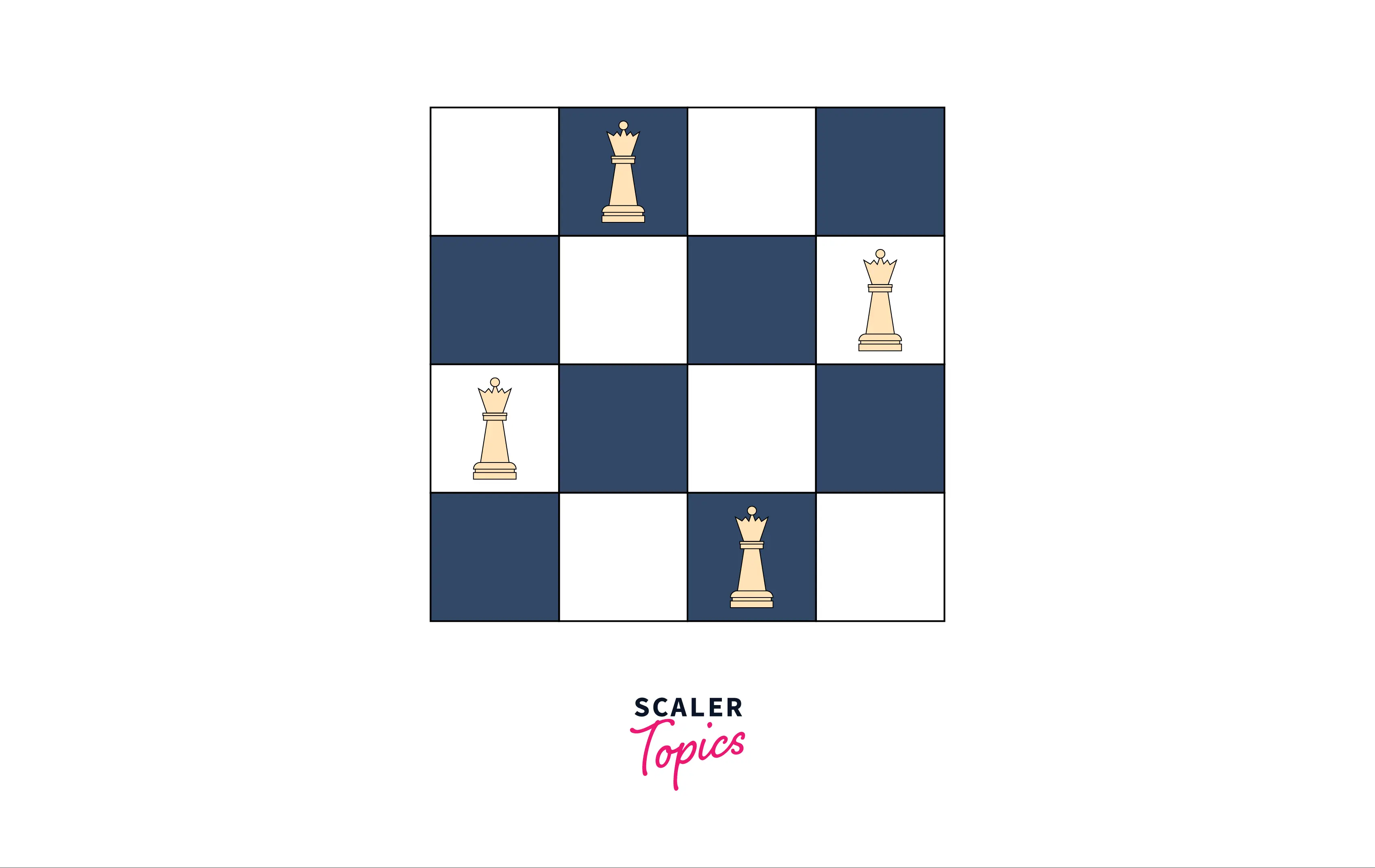
It can be seen that no queen can attack any other queen.

Example 2 -

Input - 3

Output - No Solution exists

Explanation -

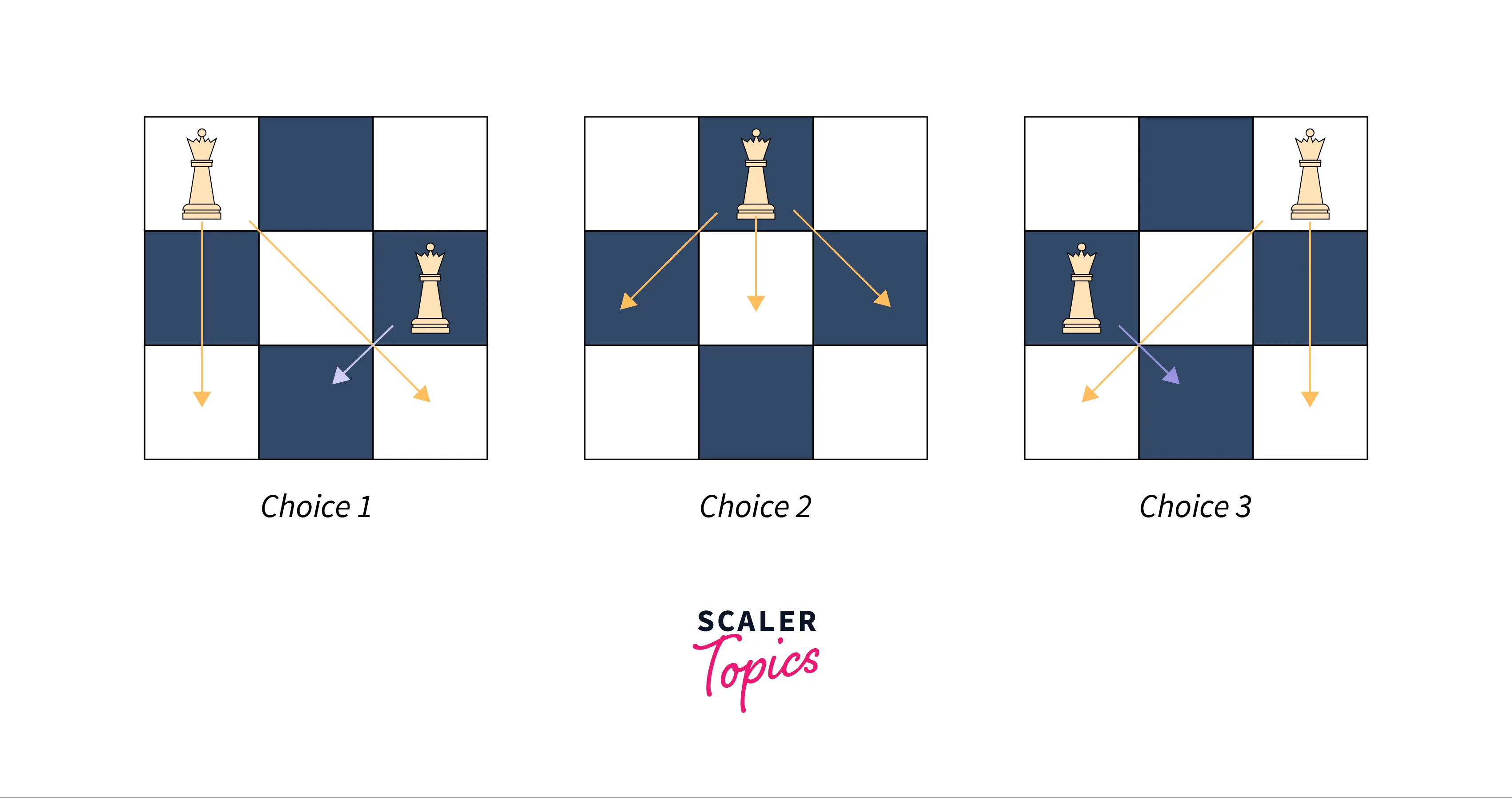
From the above image, we can say that no arrangement exists for n = 3.

Constraints

$1\leq N \leq 12$

Approach 1: Backtracking Approach

The first and the most intuitive approach is to simulate the whole process i.e. trying out all the possibilities until we've found a valid one. Before beginning with the algorithm to find the solution to the N queens problem, let's have a look at some observations -

1. Each row of the chessboard should have exactly one queen. This is because, if there are two or more queens in a single row then they can attack each other.
2. Each column of the chessboard should have exactly one queen. Again due to the same reason.

So we will try to place a queen at a valid position in each row, and then we will recur for the subsequent rows of the chessboard. If by following this method, we have placed the queens in each of the n rows, it means the solution exists.

Algorithm

The algorithm is as follows -

• Define a character array board of dimensions $N\times N$ and initialize all its entries with '.', where '.' represents the empty cell.
• Start the process from the topmost row.
• If all queens are placed return true.
• Otherwise, for each of the columns in the current row do the following -
  • If it is possible to place the queen in the current cell $i.e.$ (row, col), place a queen in this cell.
  • Check if placing the queen in the current cell leads to a valid solution. If yes, then print the solution and terminate the program.
  • Otherwise, remove the queen from the current cell.
• If all the columns are tried for a given row, Return false to trigger the backtracking.

Java Implementation

C++ Implementation

Python Implementation

Output -

Complexity Analysis

Time Complexity - Since in each row we are iterating for $N$ times and it costs O(1) time to check if placing the queen in a cell is valid. Therefore, the recurrence relation of the above algorithm is $T(N)=$ $N\times T(N-1) + N$ which evaluates to $O(N \times N!)$ Space Complexity - Since we've used the board array which is of dimensions $N\times N$, the space complexity is $O(N^2)$

Approach 2: Backtracking with Optimization in isSafe() function

In our last code, we have seen that for each cell on the board we were spending $O(N)$ time just to check if placing the queen in an arbitrary cell is valid or not using the isSafe() function. The idea is to optimize this isSafe() function by using some mathematical phenomenon. Let's see what they are -

1. Along any left diagonal, the difference between the row index and column index is constant and different for each diagonal. [IMAGE 3 START SAMPLE]

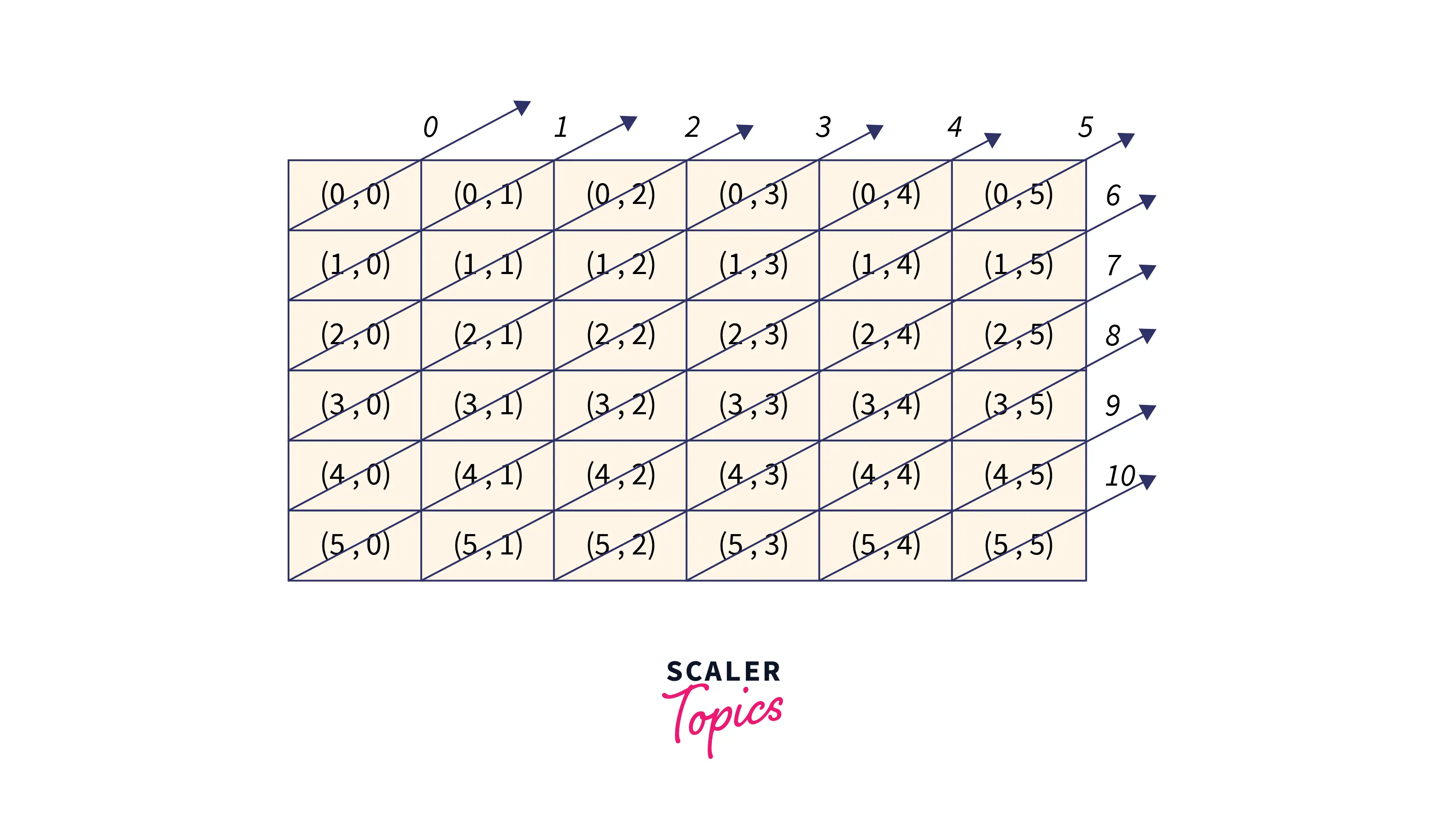
2. Along any right diagonal the sum of the row index and column index is constant and different for each diagonal.

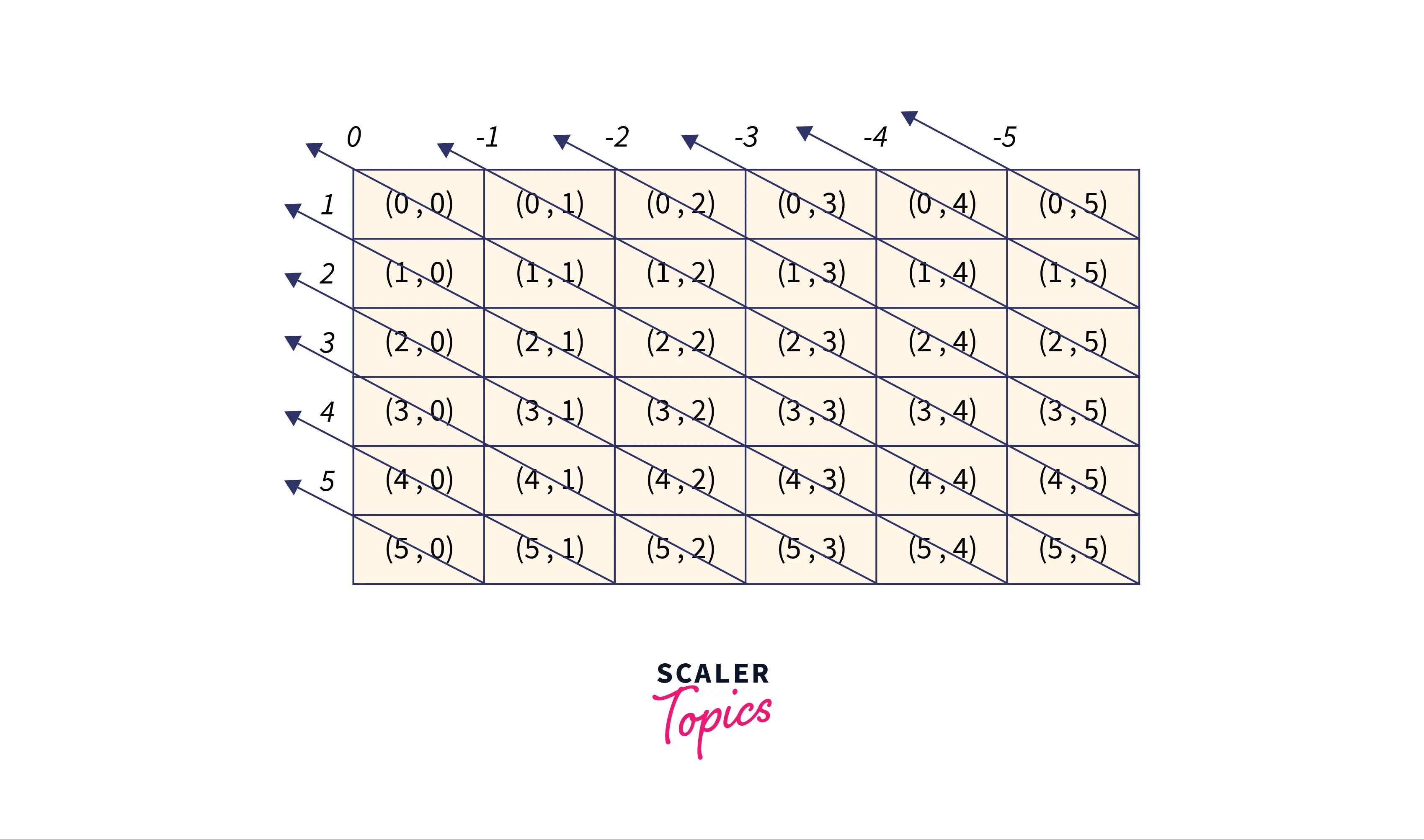
Now, it is clear that, if at any diagonal a queen is placed then we can not place any other queen on the same diagonal. So, instead of searching along the length of the diagonal every time, we will mark the diagonal if a queen is placed on it. The same goes with the column, due to which we will be able to perform the isSafe() function in $O(1)$ time.

From the image given above, it can be observed that the difference between the row index and column index for a board is in the range of [-( N - 1 ), ( N - 1 )] and if we use a boolean type array to mark diagonals we will be in trouble because array indices are non-negative. Therefore, to mark the left diagonal we will add an offset N - 1 to each value to make the index non-negative.

Algorithm

The algorithm and the code for finding the answer will be the same as the previous approach. The below-given algorithm shows the optimizations made to mark the diagonal.

1. Define three boolean type arrays Viz. leftDiagonal, rightDiagonal, and column of size $2\times N$ each to store information about the left diagonals, right diagonals, and the columns.
2. To check if a cell (row, col) is safe to place a queen. We will check if all the leftDiagonal[row - col + N -1], rightDiagonal[row + col], and column[col] are unmarked $i.e.$ False.
3. Whenever we are placing a queen in the cell (row, col), we will mark leftDiagonal[row - col + N - 1], rightDiagonal[row + col], and column[col] as True.
4. When we backtrack we will again set the above value to be False.

Java Implementation

C++ Implementation

Python Implementation

Output -

Complexity Analysis

Time Complexity - Since in each row we are iterating for N times and it costs $O(1)$ time to check if placing the queen in a cell is valid. Therefore, the recurrence relation of the above algorithm is $T(N)= N\times T(N-1)$ which evaluates to $O(N!\,)$ Space Complexity - We have used a 2-d array of dimension $N\times N$ to store the board elements, also we have used three boolean arrays of length $\theta(N)$ each. Therefore, the total space complexity is $O(N^2 + 2N + 2N + N) = O(N^2)$

Approach 3: Efficient Backtracking Approach Using Bit-Masking

In the previous approaches, we have seen that each row and column can contain at most one queen. To place a queen at any cell in the board, we must check if it attacks any other queen and check that we have used boolean arrays in our last approach. But, as per the given constraints $1\leq N\leq 12$ we can also use the bitmask approach to saving space required in boolean arrays. In this approach, we will be replacing the boolean arrays with 32-bit integers so that we can achieve the solution in constant extra space.

Let's see what is this bitmask approach -

• Define three integers which we will use to identify the safe columns to place the queen in each row.
  1. colMask - If the $i^{th}$ bit of colMask is set, then it means it is unsafe to place a queen in the $i^{th}$ column as it can be attacked by a queen placed somewhere in the same column.
  2. leftDiagonalMask - If the $i^{th}$ bit is set, then it means it is unsafe to place a queen in the $i^{th}$ column as it can be attacked by a queen placed somewhere in the left diagonal.
  3. rightDiagonalMask - If the $i^{th}$ bit is set, then it means it is unsafe to place a queen in the $i^{th}$ column as it can be attacked by a queen placed somewhere in the right diagonal. Initialize all of them with a 0 value.
• Now, to check if a cell (row, col) is safe to place the queen, we check if the $col^{th}$ bit of anyone of the mask values is set. If found yes, then it is unsafe to place the queen in the cell.
• When we place the queen in a cell (row, col) we need to modify the mask value to mark the newly formed unsafe cells in the next column (due to placing the queen in the cell). We will modify as per the following points -
  1. colMask - If we are placing the queen in the $i^{th}$ column we will set the $i^{th}$ bit of colMask.
  2. leftDiagonalMask - If we place the queen in the $i^{th}$ column we will set the $i^{th}$ bit of leftDiagonalMask and shift all its bits toward left by 1 as it has to block the next column of the next row (as it falls on the left diagonal).
  3. rightDiagonalMask - If we place the queen in the $i^{th}$ column we will set the $i^{th}$ bit of rightDiagonalMask and shift all its bits toward the right by 1 as it has to block the previous column of the next row (as it falls on the left diagonal).

Java Implementation

C++ Implementation

Python Implementation

Output -

Complexity Analysis -

Time Complexity - Since in each row we are iterating for N times and it costs O(1) time to check if placing the queen in a cell is valid. Therefore, the recurrence relation of the above algorithm is $T(N)=$ $N\times T(N-1)$ which evaluates to $O(N!\,)$ Space Complexity - Since, we are using a 2-dimensional array of dimension $N\times N$, therefore the overall time complexity is $O(N^2)$. However, we can say that constant extra space is required to find the answer (if we do not account space needed to store the answer).