Pattern Program in Java

Introduction to Pattern Programs in Java

Now, why do we need to learn this topic separately, we can just copy and paste the pattern?

Besides defying the whole purpose of the Pattern Programs, Copying can only be done for constant size. For Pattern Programs in Java, we take the size as an input.

Pattern Programs in Java are generally solved with nested loops, mostly we will be using for loops because of their convenience, but while and do-while loops can also be used. Using these loops and control structures, you can learn how to print pattern designs in Java by generating different outputs based on the input size.

We can divide the Pattern Program in Java, into 3 basic categories:

• Star Patterns
• Number Patterns
• Character Patterns

For each of these categories, you can use Java code to print pattern outputs, demonstrating how to print pattern step-by-step using loops and basic syntax.

Creating Patterns

To create patterns in Java, a solid grasp of loops, conditional statements, and variables is essential. Loops—such as for, while, and do-while—play a crucial role in controlling the number of rows and columns, which directly affects the structure of the pattern. For example, the outer loop typically manages the number of rows, while the inner loop handles the columns or the number of elements printed per row.

Conditional statements, like if-else, are used to determine what should be printed at each position—be it a star, number, character, or even a blank space. This is especially important for creating patterns with specific requirements, such as hollow shapes or alternating symbols.

Variables, such as integers for counting rows and columns or characters for printing alphabets, are used to store and manipulate the values needed for the pattern. By combining these elements, you can control the number of rows, manage the flow of the pattern, and use conditional statements to create intricate and customized designs in Java.

Types of Patterns

Pattern programs in Java can be broadly classified into several types, each offering unique ways to create visually engaging outputs. The most common categories include star patterns, numeric patterns, and character patterns.

• Star patterns involve printing asterisks (*) in various shapes and arrangements, such as squares, triangles, diamonds, and more. These patterns are a great way to practice controlling output using loops and are often the first step in learning pattern programs.

• Numeric patterns focus on printing numbers in specific sequences or arrangements. Examples include printing multiplication tables, number pyramids, or even Fibonacci sequences. These patterns help reinforce logic building and manipulation of numeric data in Java.

• Character patterns require printing alphabets or symbols in structured formats. Whether it’s printing the alphabet in a triangle or creating a pattern with custom characters, these programs help in understanding ASCII values and character manipulation.

Understanding these different types of patterns is crucial for mastering pattern programs in Java, as it allows you to create various shapes and designs, and lays the foundation for more complex pattern generation.

Pattern Variations

Pattern variations are all about taking basic patterns and transforming them into new, interesting designs. For instance, a simple star pattern can be adapted to form a hollow diamond shape or a pyramid shape by adjusting the logic in your loops and conditional statements. Similarly, character patterns can be modified to print sequences like A, B, C, D, or even spell out words in a specific arrangement.

Numeric patterns can also be varied to display multiplication tables, Pascal’s Triangle, or other mathematical sequences. By experimenting with the placement of spaces, stars, numbers, or characters, you can print a wide range of patterns—from classic right-angled triangles to complex diamond shapes and beyond.

Exploring different pattern variations not only enhances your understanding of Java programming but also allows you to create unique and visually appealing outputs that stand out.

Star Pattern Programs in Java

Star Pattern Program in Java generally asks us to print * (asterisk) in different shapes and forms. Most commonly we see a mixture of squares, rectangles, and triangles in these patterns.These pattern prints, such as the pyramid star pattern, are commonly used to practice output formatting in Java. Let's understand it with the help of an example of a star pattern.

Example 1: Right-angled Triangle of * (Left)

Pattern:

Observation:

Here we can observe that we need a nested pair of loops, to print columns and rows.

Let's discuss the conventions that we (generally) follow:

• As we can see from the pattern, we will be requiring nested loops. We can use while, do-while, or for loops for this purpose, for simplicity, we will be using for loops.
• We will be using i,j,k,.. as loop variables for generalizing. i is the outermost loop, and j,k... are inside it.
• Since 'i' is the outermost loop, it deals with rows.
• And since 'j' is the inner loop, it deals with columns.
• We always try to break a big pattern into smaller ones.
• If there are some spaces in the pattern, then we replace them with '-' or any other character in rough. It will help us to correctly solve the pattern.

Explanation: Here, we can observe that the 1st row has 1 star, the 2nd has 2 stars, and ith row has i stars. This pattern is also known as a right triangle star pattern.Therefore, we can print i stars in every row.

We will achieve this by running the inner ('j') loop 'i' times.

Our loop structure will look like this:

Code:

Example 2 : Print Square Grid of Stars

Pattern:

Observation:

Here we are required to print a square of '*' of size n×n. So for doing so, we will use nested for loops. We want to leave a line after every 'n' stars.After printing each row of stars, a new line is inserted to move to the next row.

Explanation:

We have to print n stars in every row. So our outer loop will iterate 'n' times and the inner loop will also iterate 'n' times.

Example 3 : Inverted Right Angled Triangle of * (left)

Pattern:

Observation:

Here, we can observe that the stars are decreasing with an increase in the value of 'i'.

Explanation:

We want to print (n-i+1) stars in each row. So our outer loop will iterate ‘n’ times and the inner loop will iterate (n-i+1). Each row starts with a specific number of stars, and as the row number increases, the row starts with fewer stars, forming the inverted

Example 4 : Right Angled Triangle of * (Right)

Pattern:

Observation: This pattern is very similar to Example 1. The difference is the space part. We need to print the space triangle as well. To deal with spaces, let's first replace them with '-'.

Now we can observe that the space triangle is similar to Example 3.

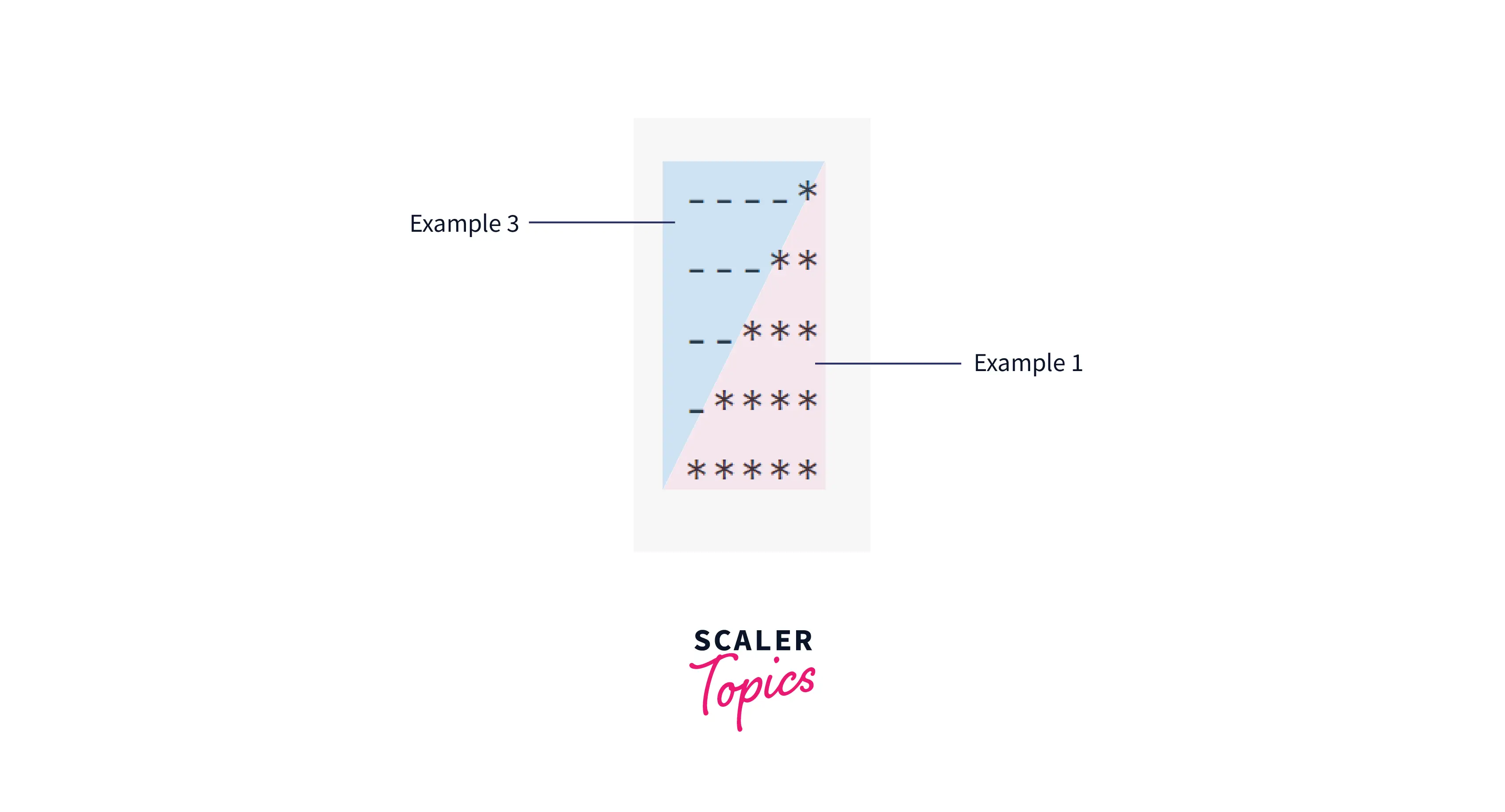
Explanation:

This pattern is also known as a half pyramid due to its shape.

We want to club 2 triangles side by side (Space triangle, and Star Triangle). Therefore the rows do not change. So we want will have to limit the outer loops to 1.

So our outer loop will iterate n times. For inner loops, we will need 2 of them for the 2 triangles.

check out the Apriori Algorithm in Data Mining, which uses nested iterations to find frequent item sets.

The spaces loop will be very similar to Example 3 (The only difference is it is printing spaces). It will iterate (n-i) times, since we want n-1 spaces in 1st row, n-2 in 2nd row,.. and n-n (=0) in the last row.

Star loop is very similar to Example 1. It will iterate i times.

Example 5 : Inverted Right angled Triangle of * (Right)

Pattern:

Observation:

This pattern looks similar to Example 3 in terms of the number of stars in each row. The difference is the space part. We need to print the space triangle as well.

To deal with spaces, let's first replace them with '-'.

Now we can observe that the space triangle is similar to Example 1. Let's divide it into smaller patterns.

Explanation: This pattern is a type of inverted pyramid, where the number of stars decreases with each row. We want to club 2 triangles side by side (Space triangle, and Star Triangle). Therefore the rows do not change. So we want will have to limit the outer loops to 1.

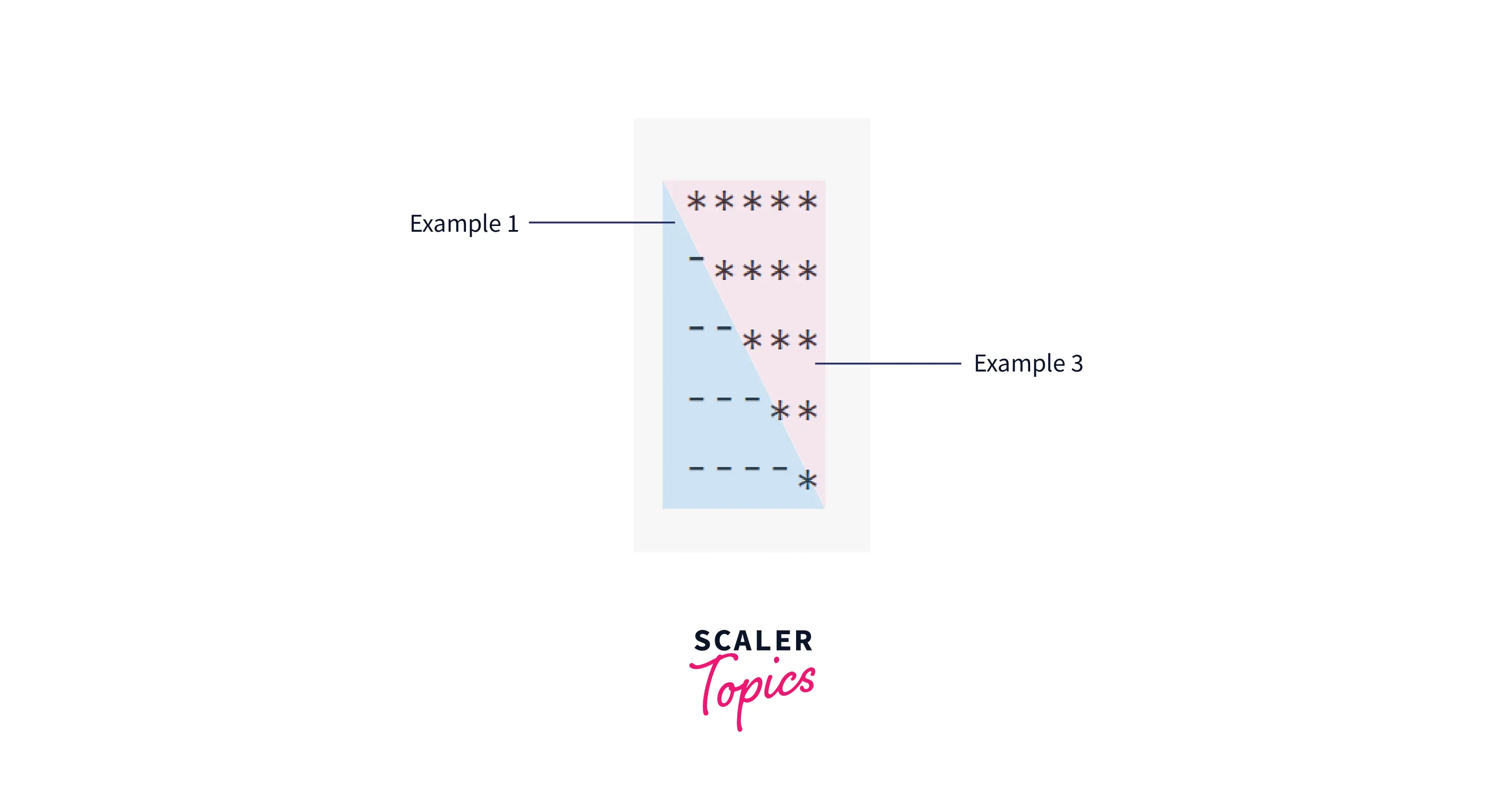
Explanation: We want to club 2 triangles side by side (Space triangle, and Star Triangle). Therefore the rows do not change. So we want will have to limit the outer loops to 1.

So our outer loop will iterate n times. For inner loops, we will need 2 of them for the 2 triangles.

The spaces loop will be very similar to Example 1. We will iterate it till i-1 since the 1st row has 0 spaces, the 2nd row has 1 space,.. ith row has i-1 spaces.

Star loop is very similar to Example 3. It will iterate n-i+1 times.

Example 6 : Arrowhead (Left)

Pattern:

Observation: This pattern is a combination of patterns of Example 1 and Example 3. We can divide it like this:

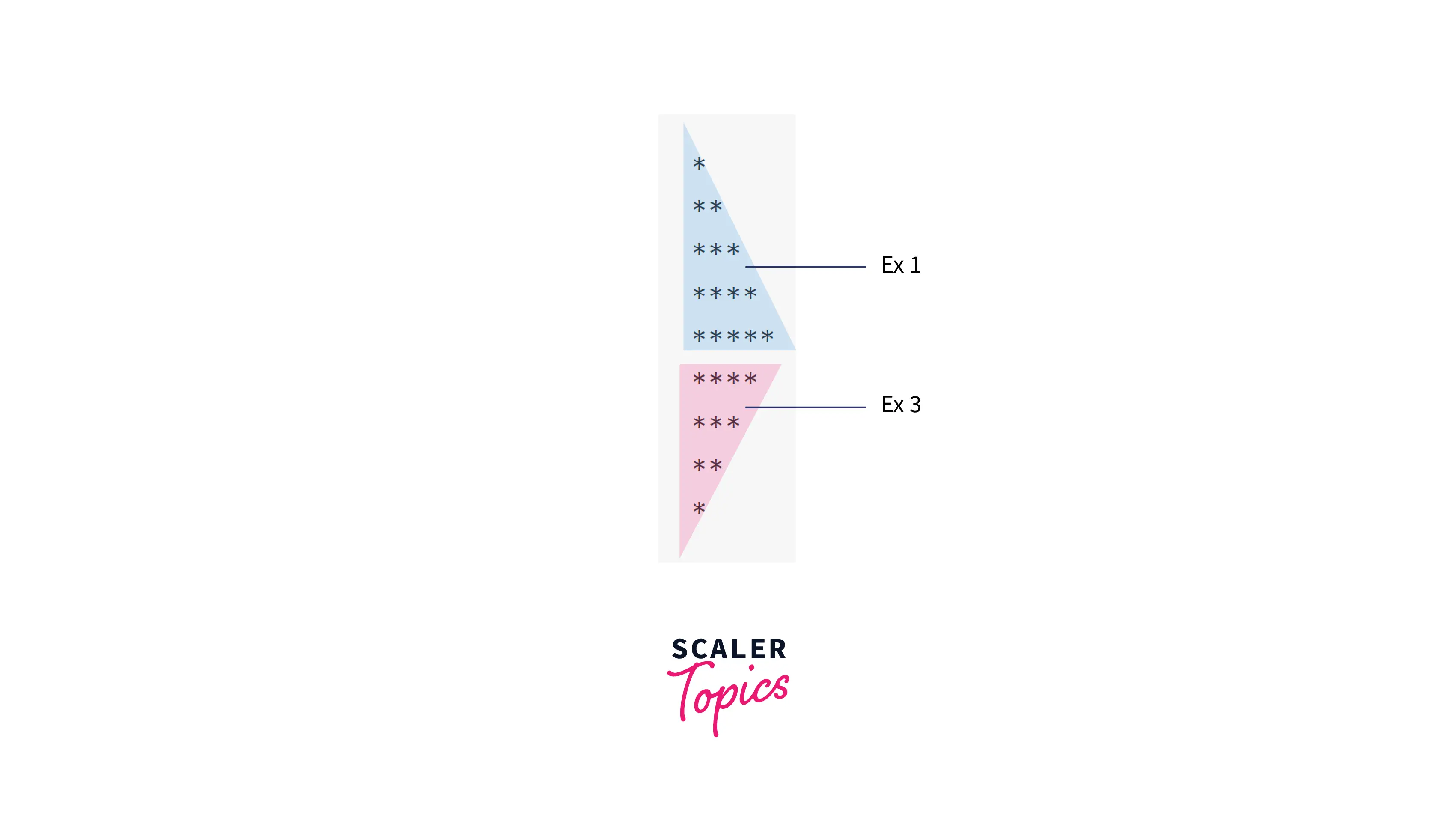
Explanation:

Since we don't have to print these 2 patterns side by side, and instead, we need to print it one after the other, we can use 2 nested loops. Nested Loop 1 for 1st triangle, similar to Example 1, of size n.

Nested Loop 2 for 2nd triangle, similar to Example 3, of size n-1, since 1 row is overlapping.

Example 7 : Arrowhead (Right)

Pattern:

Observation: It looks like patterns we have done earlier. It will be more clear once we replace spaces with '-'.

We can see that it is a mixture of 4 triangles, where all smaller triangles are similar to Example 1 and Example 3. Now we can divide this pattern into 2 or 4 patterns like this:

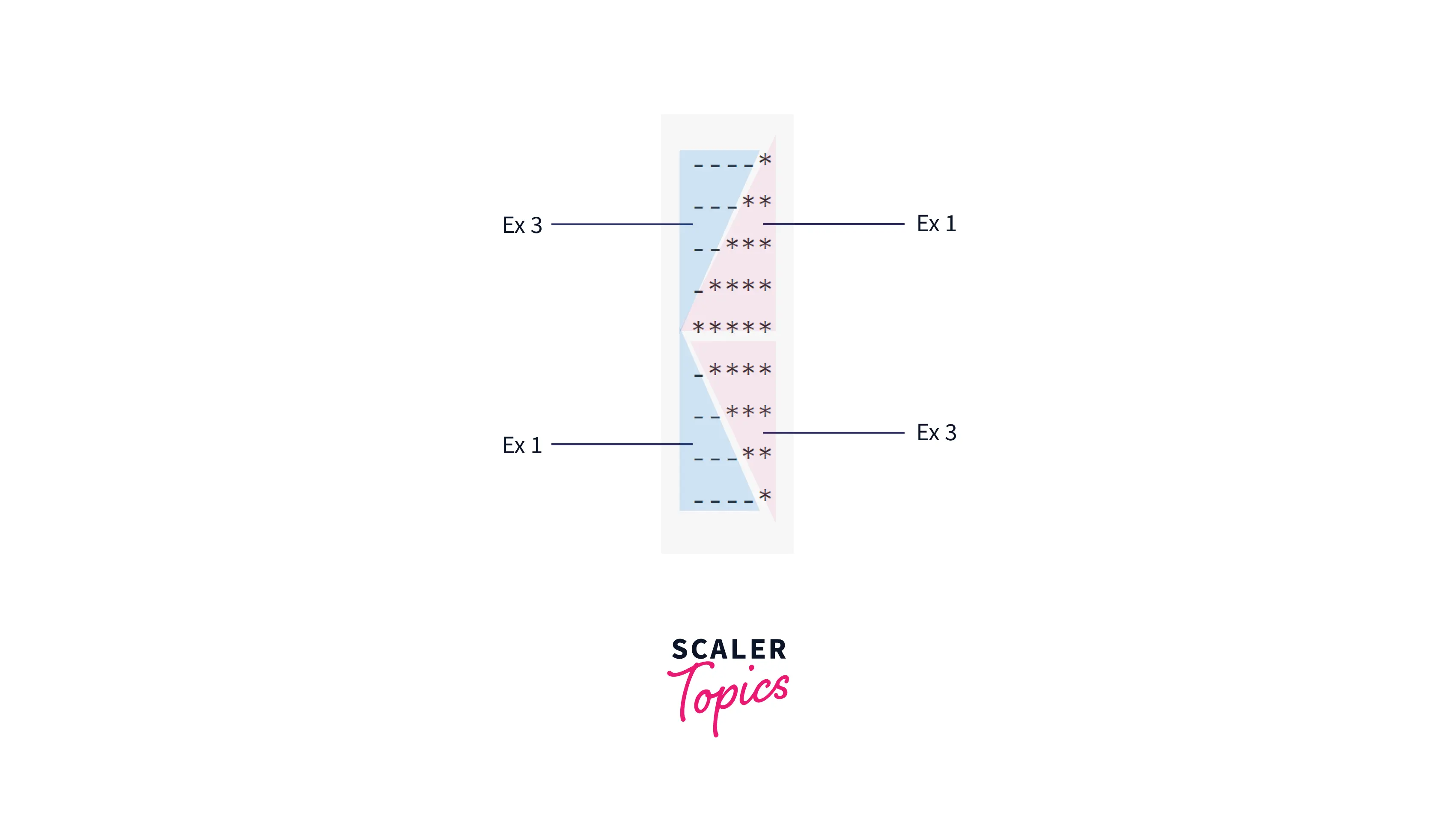
Explanation: We can see that we need to print 4 triangles, 1 and 2 side by side, and 3 and 4 side by side. Therefore we will need 2 pairs of nested loops.

1st nested loop will iterate for n times and print 2 triangles:

• a space triangle of size n-1, similar to Example 3.
• a star triangle of size n, similar to Example 1.

2nd nested loop will iterate for n-1 times and print 2 triangles:

• a space triangle of size n-1, similar to Example 1.
• a star triangle of size n-1, similar to Example 3. (Size is n-1 Since 1 row is overlapping)

Example 8 : Valley

Pattern:

Observation: It looks like star triangles and 1 space triangle. For understanding the space triangle, let's replace spaces with '-'.

So we can divide the pattern into 3 patterns:

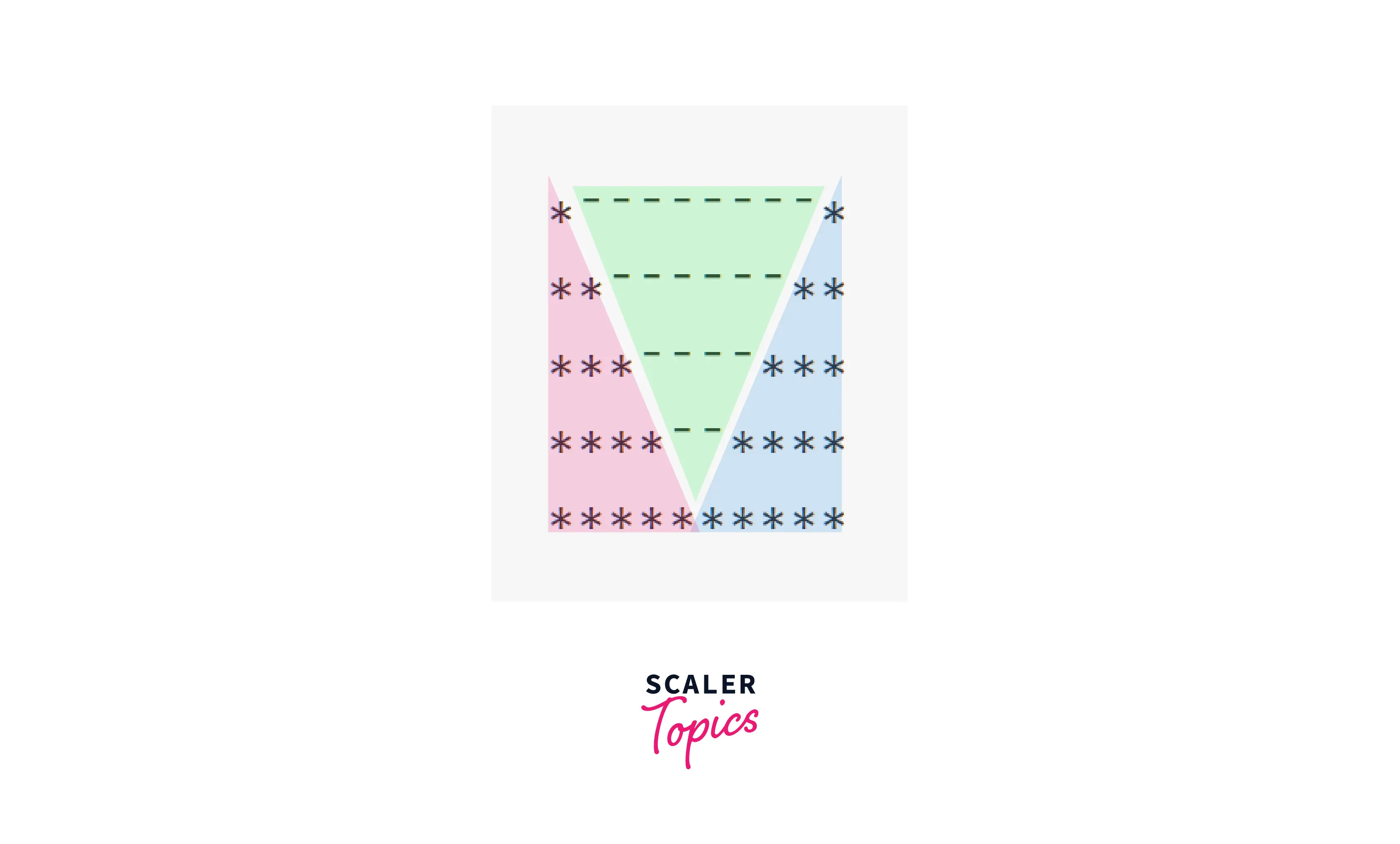
Explanation: Since we want to print the triangles side by side, we will have to use 1 outer loop and then divide the pattern into 3 parts.

3 parts:

Both the star triangles are similar to Example 1, of size n.

The space triangle is similar to Example 3 but we need to print 2 spaces instead of 1. This can easily be observed because we want: 2*(n-1) spaces in 1st row, 2*(n-2) spaces in 2nd row, 2*(n-i) spaces in ith row. Therefore, the size of the space triangle is n-1.

The bottom section of the pattern is called the lower pyramid. This lower pyramid forms the inverted or downward-expanding part of the symmetrical star pattern, completing the sandglass or hourglass shape.

Example 9 : Inverted Valley

Pattern:

Observation: This pattern is the reverse of the last pattern. And so it looks like we can divide into 2 star triangles, and 1 space triangle. For understanding the space triangle, let's replace spaces with '-'.

So we can divide the pattern into 3 patterns:

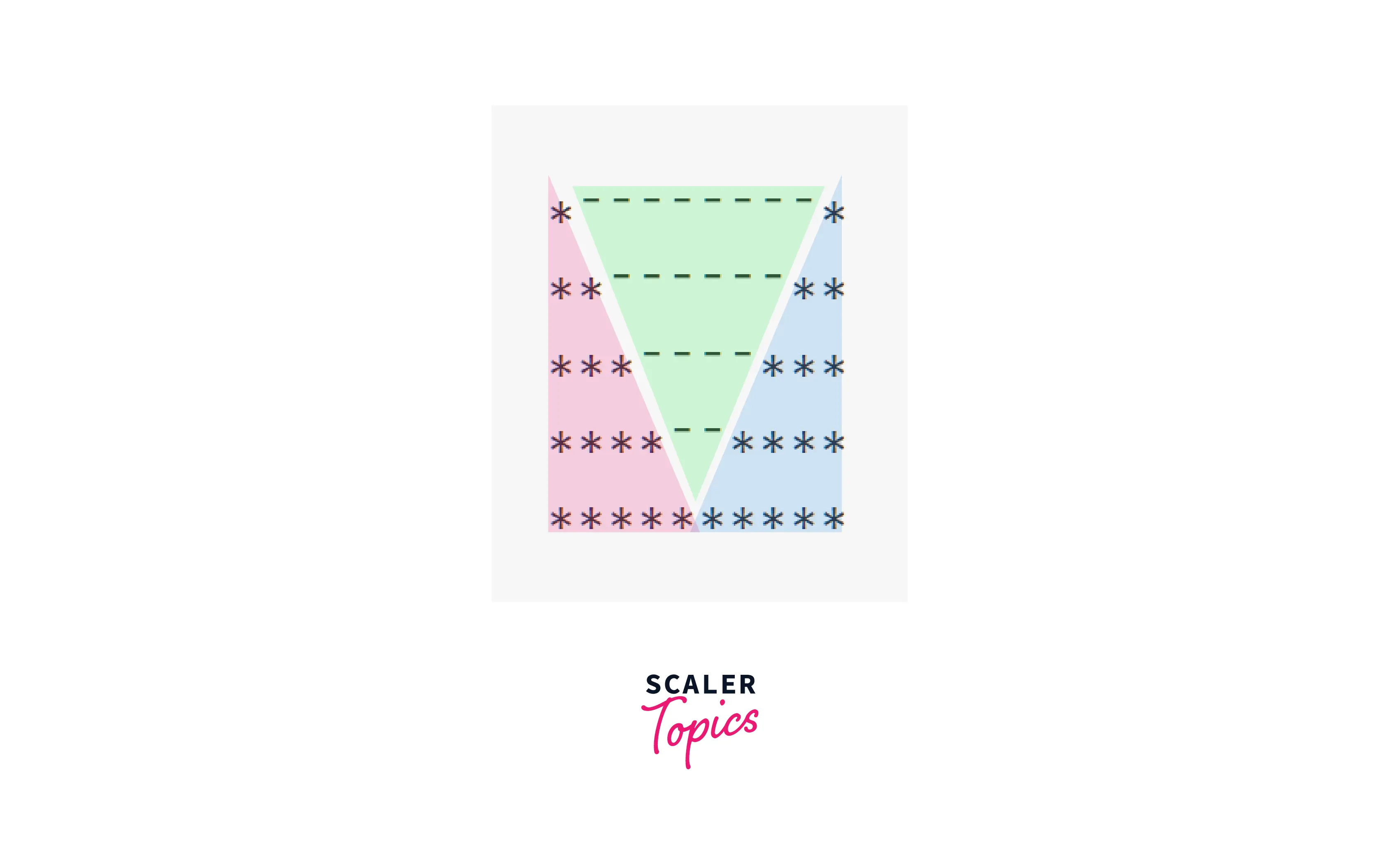
Explanation: Since we want to print all the 3 triangles side by side, we will have to use only 1 outer loop.

Since we have only 1 outer loop, and this pattern can be easily achieved by inverting the last pattern, we can just reverse the outer for loop, i.e.,

And we can also deal this as a new problem.

3 Parts:

Both the star triangles are similar to Example 3, of size n. Iteration for n-i+1 times.

The space triangle is similar to Example 1 but we need to print 2 spaces instead of 1. This can easily be observed because we want: 0 spaces in 1st row, 2 spaces in 2nd row, 2*(i-1) spaces in ith row. Therefore, the size of Space triangle is n-1.

Example 10 : Hollow Diamond

Pattern:

Observation: This looks like a combination of last 2 patterns. Let's replace all the spaces with '-', to observe the pattern.

Now, let's try to break it down into simpler patterns.

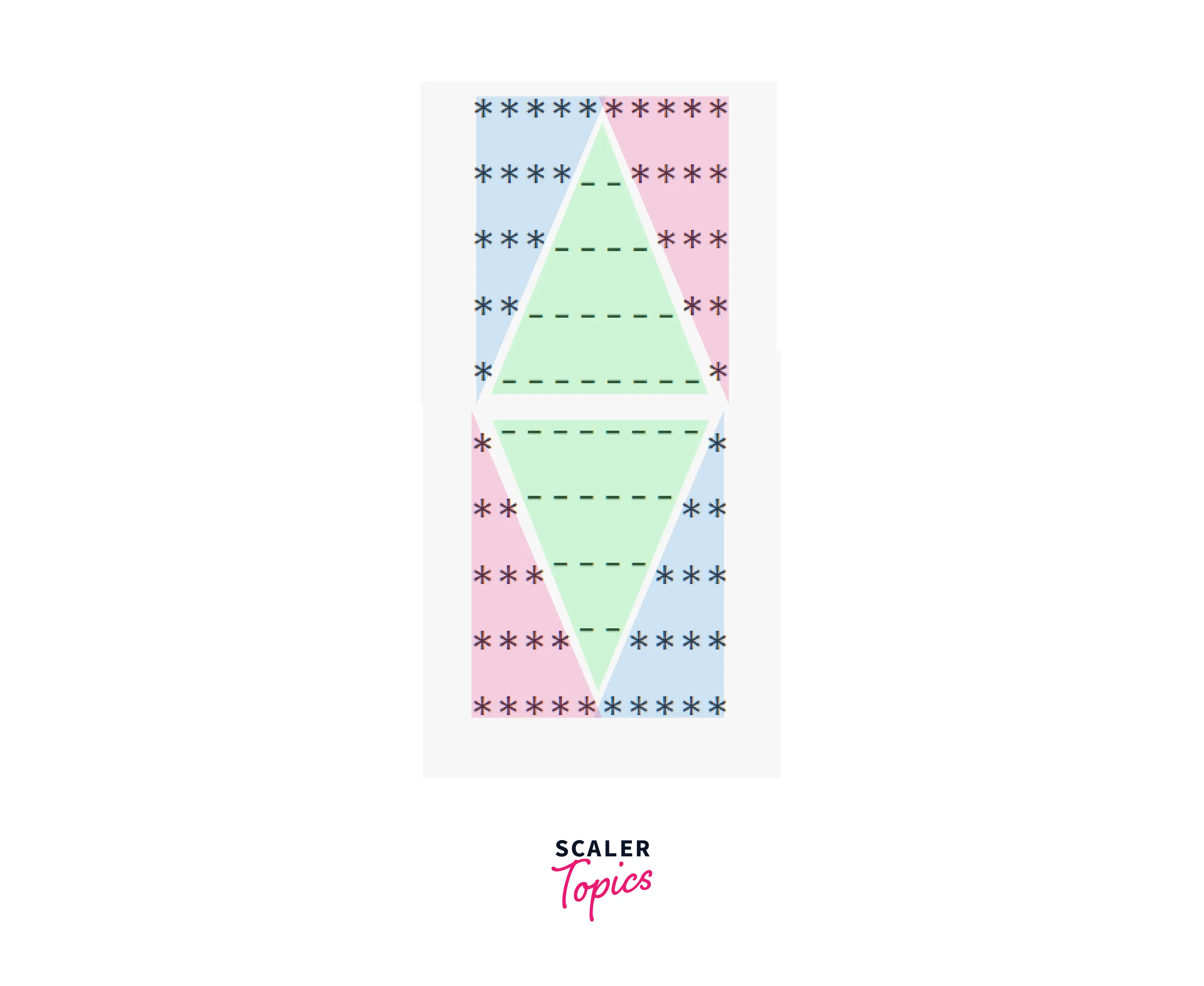
While doing so, we can see that this is nothing but a combination of previous 2 patterns.

Explanation: The hollow diamond pattern is formed by combining two pyramid patterns, one upright and one inverted, which creates its characteristic symmetry. Since we want to print the 2 patterns one after the other, we will use 2 pairs of nested loops. One from Example 8 and other from Example 9.

The spaces are doubled.

Example 11 : Spaced Pyramid

Pattern:

Observation: This shares similarities with Example 1, since we have 1 star in 1st row, 2 stars in 2nd row, and i stars in ith row. To understand spaces, let's replace all the spaces with '-'.

This is an example of a pyramid star pattern. We can see that we need to print a space triangle, similar to Example 3. And we also need to print stars with a space attached.

Now, lets try to break it into simpler patterns.

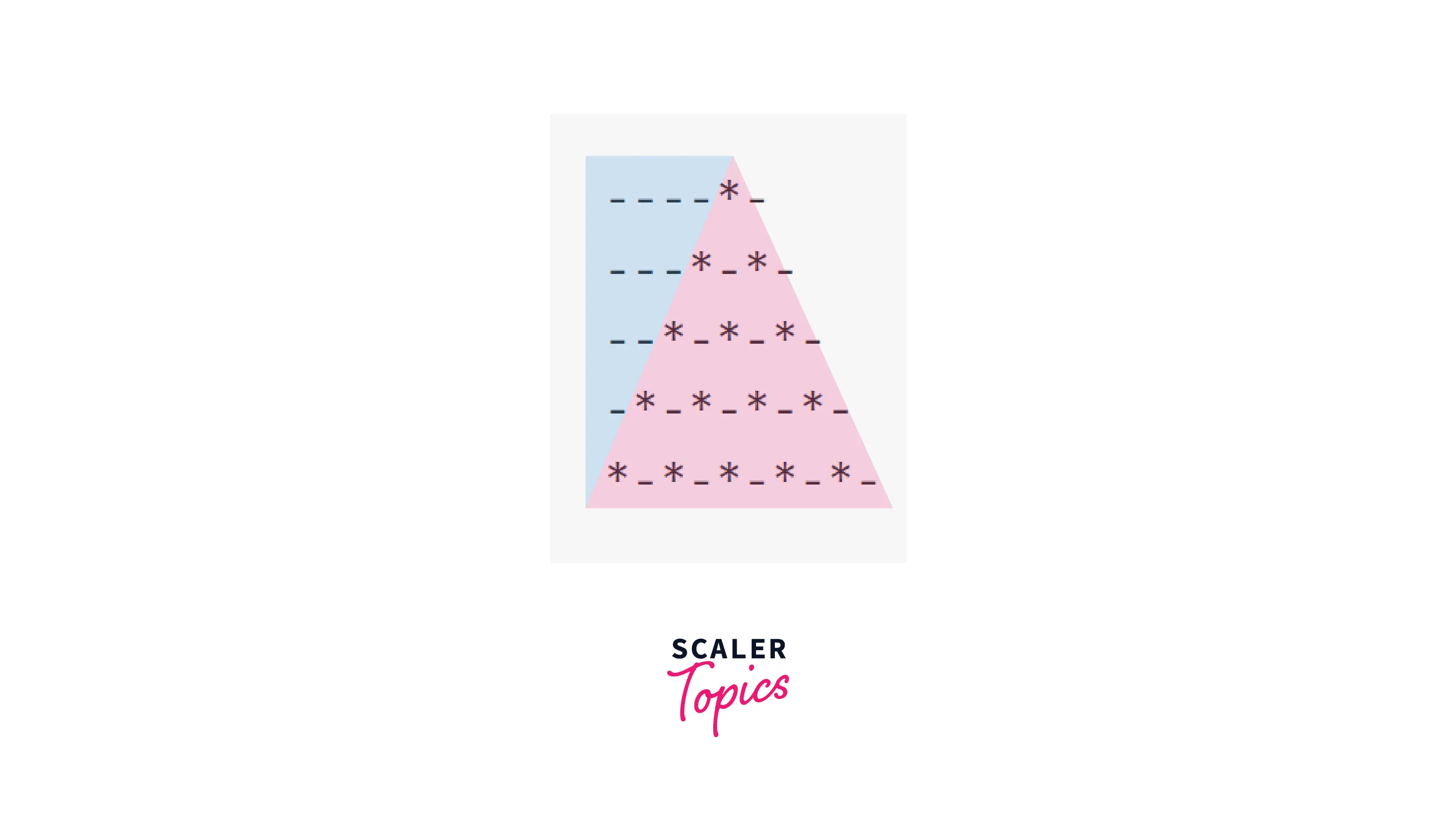
Explanation: Since space and star triangles are sides by side, we will limit the number of outer loops to 1.

Space loop will be similar to Example 3, of size n-1.

Triangle loop will be similar to Example 1, of size n. There is an extra space with each '*'.

Example 12 : Inverted Spaced Pyramid

Pattern:

Observation: This pattern is just the inverted version of last pattern. We can divide it into 2 triangles. Let's replace all the spaces with '-'.

Now, lets try to break it into simpler patterns.

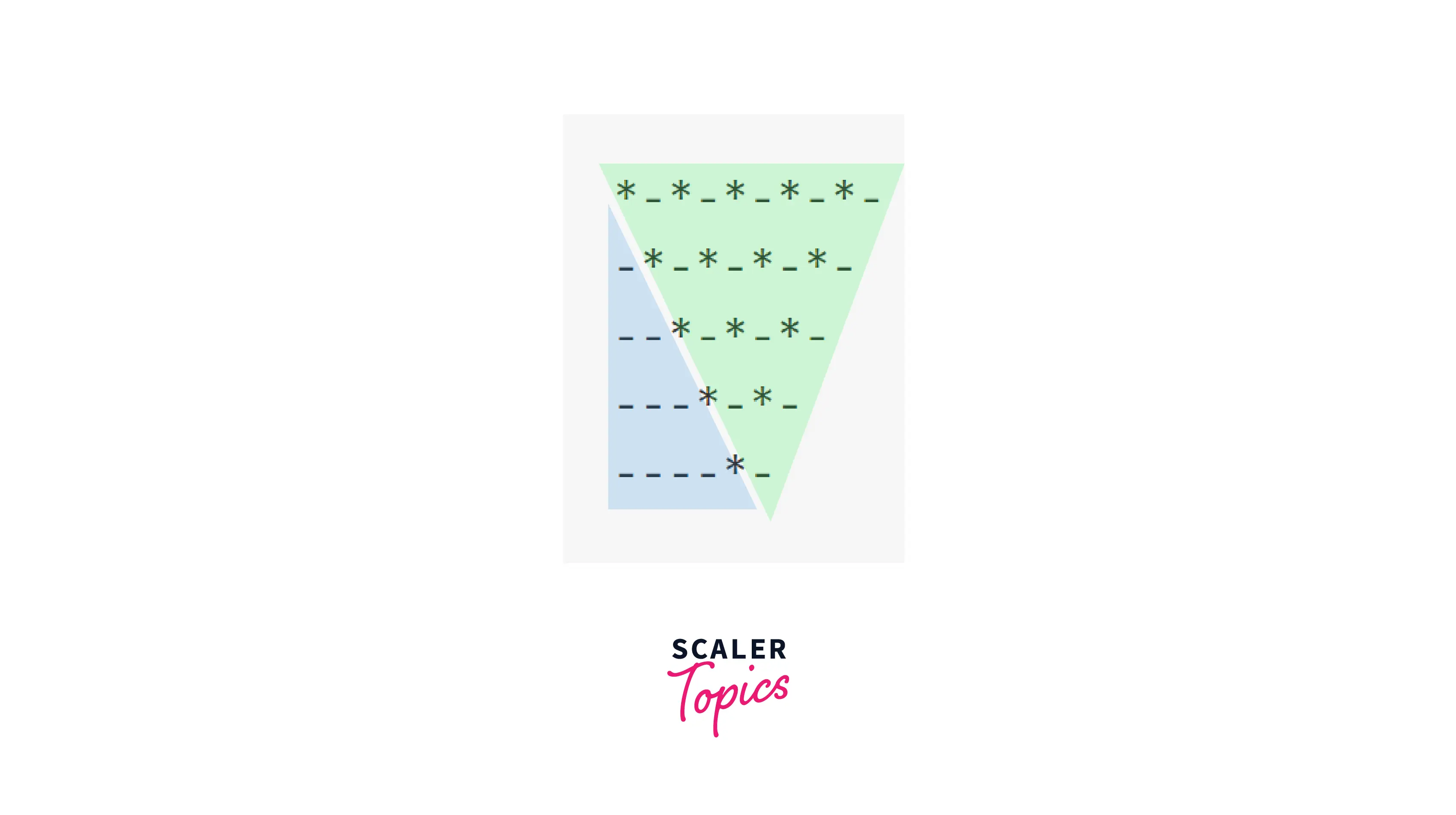
Explanation: Since we have only 1 outer loop (as both the triangles are printed side by side), we can invert the outer loop like this:

We can also approach it by breaking into smaller patterns.

Space loop will be similar to Example 1, of size n-1.

Triangle loop will be similar to Example 3, of size n.

There is an extra space with each '*'.

Example 13 : Hourglass

Pattern:

Observation: We can see that this pattern is a combination of last to patterns. Let's replace all the spaces with '-'.

Now, let's try to break it into simpler patterns.

Explanation: We can see that in this pattern, we are printing Example 11 and Example 12, one after other. Therefore, we will use 2 pairs of nested loops for the 2 parts.

Loop 1 will be similar to Example 11. Loop 2 will be similar to Example 12

There is an extra space with each '*'.

Example 14 : Spaced Triangle

Pattern:

Observation: In this pattern, stars are related to rows as: 1st row has 1 star, 2nd row has 3 stars, ith row has (2i - 1) stars.

Let's replace all the spaces with '-'.

Let's divide into 2 triangles.

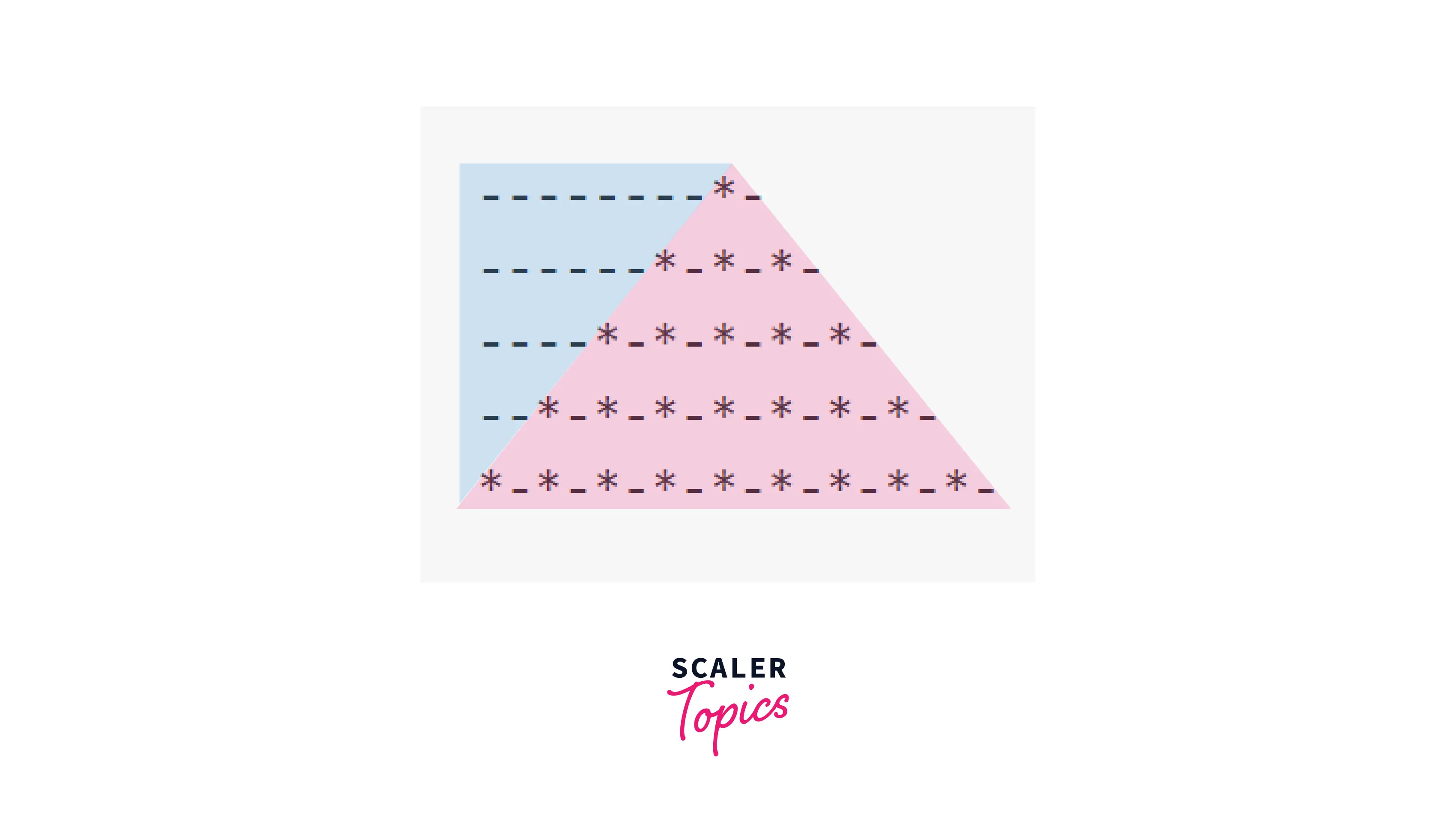
Explanation: In this pattern we have to deal with 2 triangles.

Space triangle is of size (n-1), and is printing 2 spaces. It is similar to Example 3, with difference being the number of spaces.

Star triangle is of size n, it is printing "*" with a space. It is iterating for (2i-1) times as discussed before.

Example 15 : Inverted Spaced Triangle

Pattern:

Observation: This pattern is the reversed version of the last pattern. Let's replace all the spaces with '-'.

Explanation: We can just reverse the outer loop and it will do the trick. We can also divide it into 2 triangles. Since we want to print them side by side, we will use only 1 outer loop.

We need to print:

A space triangle of size (i-1), similar to Example 1, with the difference being in the number of spaces.

A star triangle of size n. Since we want to print the reverse triangle, we can come up with many relations. One such relation is to print 2(n-i+1)-1* stars in every column.

Takeaway: (n-i+1) is very common while printing a pattern that is decreasing.

Example 16 : Diamond

Pattern:

Observation: This pattern is a combination of last 2 patterns. Let's replace all the spaces with '-'

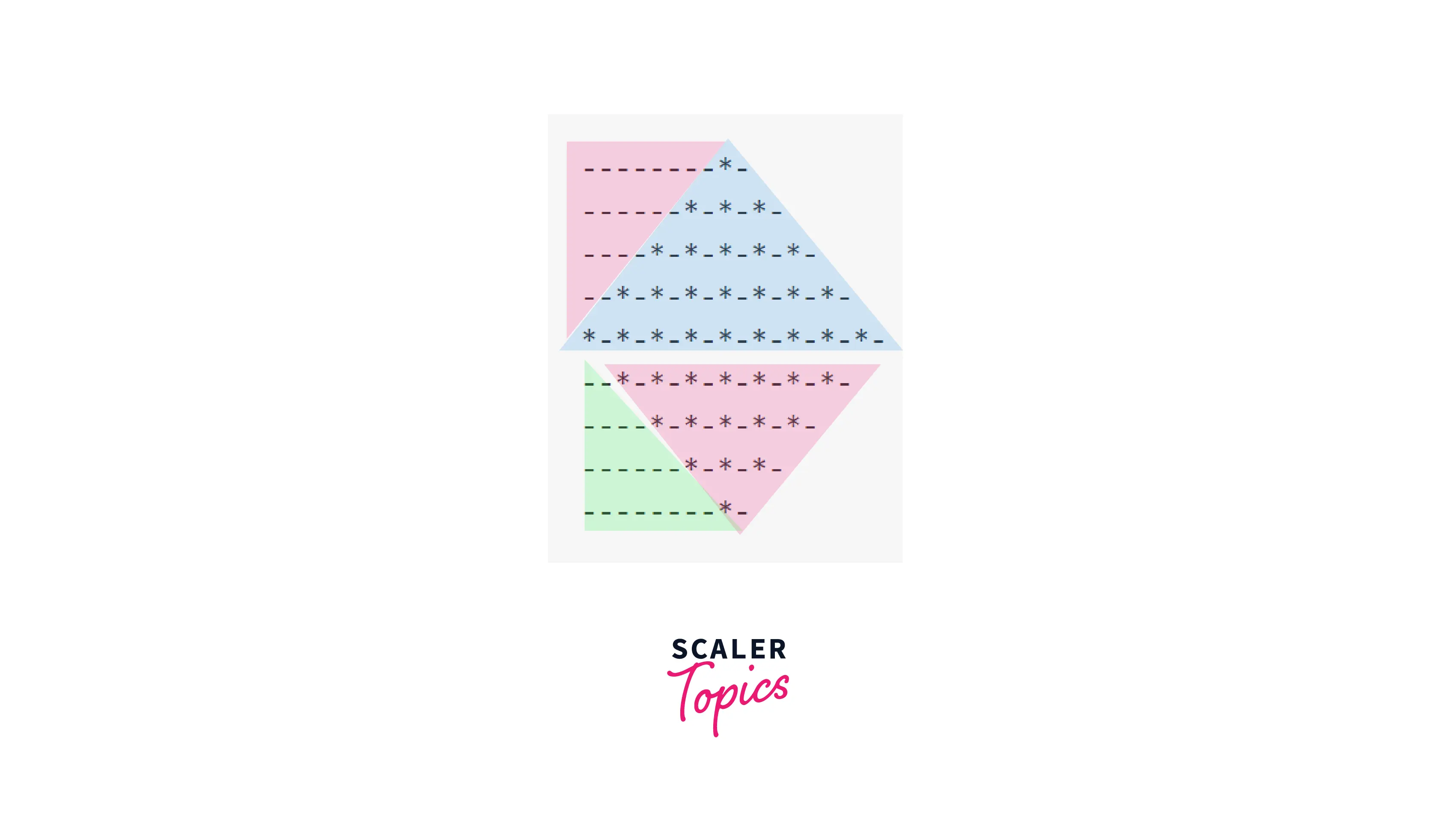
We can see that this pattern is nothing but combination of last 2 patterns.

Explanation: We will use 2 nested loops for 2 parts. Loop 1 similar to Example 14, of size n. Loop 2 similar to Example 15, of size n-1. It is because 1 row is overlapping.

Example 17 : Hollow Rectangle

Pattern:

Observation: We can observe that we want to print a n*n matrix, with some constraints. We don't want to print any stars in the interior. Let's replace all the spaces by '-'

We can see that we don't want to print a star anywhere except the border.

Explanation: So we can use an if for checking if "i is 1" or "j is 1" or "i is n" or "j is n", then only we will print the star.

The size of the pattern is n*n.

Example 18 : Hollow Right Angled Triangle (Left)

Pattern:

Observation: This pattern is similar to Example 1. But, here we want to print stars only in borders. Let's replace all the spaces with '-'.

Explanation: We can see that stars are just in the borders. So again, we will use an if statement.

Loops are very similar to Example 1. Outer loop will iterate n times, and the Inner loop will iterate i times.

Example 19 : Hollow Right Angled Triangle (Right)

Pattern:

Observation: This pattern is a combination of Example 18 and Example 3. Let's replace all the spaces with '-'.

We can divide it like this:

We can see that stars are just in the borders. So again, we will use an if statement. But here we also have to print a space triangle.

Explanation:

Since the space triangles and star triangles are printed side by side, we will limit the number of outer loops to 1. We will print a space triangle, similar to Example 3, of size n-1.

The space loop will iterate for n-i times.

The star part is similar to Example 18.

Example 20 : Hollow Arrowhead (Left)

Pattern:

Observation: It looks like that one part of this pattern is very similar to Example 18. To understand the pattern properly, let's replace all the spaces with '-'.

We can see that stars are just in the borders. Let's divide it into smaller patterns.

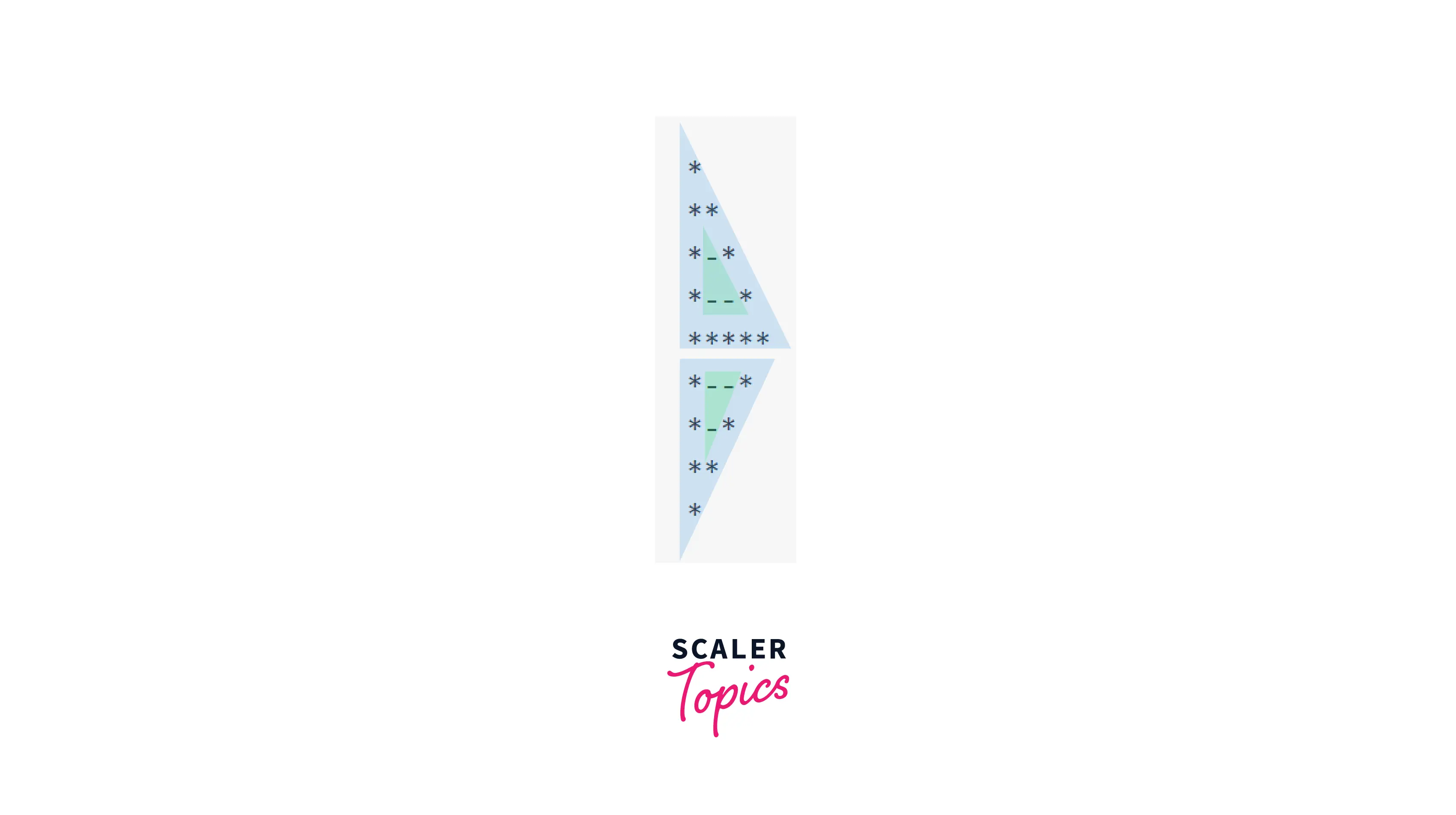
Explanation: We will use 2 pairs of nested loops to display the 2 parts.

Size of the upper triangle is n. Since there are i characters in ith row, we will iterate the inner loop for i times, and the outer loop for n times. For spaces, we will have to keep a check, if j is 1 or j is I, then we will print stars, else, print spaces.

For the lower triangle, we can see that we have 1 row overlapping, so we will print a decreasing triangle, similar to Example 3. Outer loop will iterate for n-1 times. We also have to take care of the spaces. So, j loop will iterate for n-1 times, and if j is 1 or j is n-i, we will print stars, else, print spaces.

Example 21 : Hollow Arrowhead (Right)

Pattern:

Observation: This pattern looks like a combination of the last pattern and the spaces triangles look like something we have delved into before. To better understand the spaces, let's replace all the spaces with '-'.

As we can see that space triangles are very similar to Example 1 and Example 3. Let's divide the pattern into smaller patterns.

Explanation: Just like the Example 20, we will divide this pattern into 2 halves, upper and lower. With the upper half, we will have to print a space triangle similar to Example 3, of size n-1. For the lower half, we will have to print a space triangle similar to Example 1, of size n-1.

Example 22 : Arrow (Left)

Pattern:

Observation: This pattern is very similar to Example 20, the difference being the row of stars in middle. As we do in every pattern, let's replace all the spaces with '-'.

To print the pattern, we can divide it into 2 halves (upper and lower).

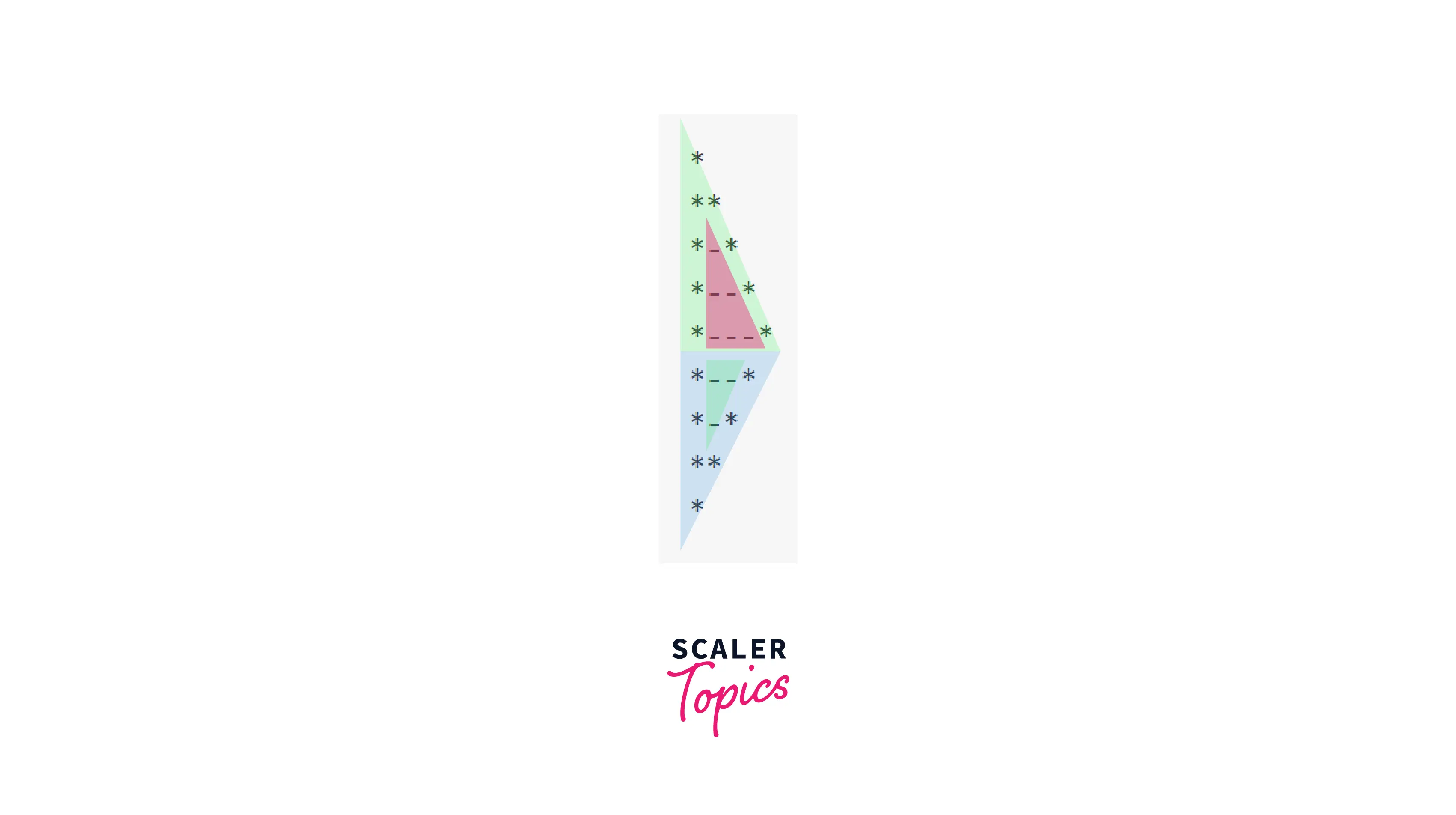
Explanation: We will use 2 pairs of nested loops for the 2 halves. Let's take reference to Example 20, and solve this pattern. We just want to print a row of stars in the last row of the upper triangle. We will achieve it with the help of it. We will check that if j is 1, or j is i or i is n, print star, else print space.

Example 23 : Arrow (Right)

Pattern:

Observation: This pattern is very similar to the last pattern, but differs in spaces. For understanding space, let's replace all the spaces with '-'.

Let's break this down into smaller patterns.

Explanation: This pattern is very similar to the last pattern, we just have to take care of 2 space triangles.

We will use 2 pairs of nested loops for the 2 halves.

For the upper half, the space triangle is of size n-1 and it is very similar to Example 3.

And for the lower half, the space triangle is of size n-1 and it is very similar to Example 1.

Since the space triangles and the pattern are side by side, we don't have to make separate nested loops, we will club into the 2 nested loops used for the upper and lower halves.

Number Pattern Programs in Java

Now that we have seen the examples of star patterns, let's play with numbers.

In Number Pattern Programs in Java, we are given a pattern that has some number series in it, and we need to print it in a specific way. It's just that we need to change the above logic so that it prints numbers instead of * this this.

To print numbers in these patterns, we use loops to control how the numbers are printed, allowing us to create various pattern prints with different numbers printed in each row or column.

Example 24 : Grid of numbers (Increasing row wise)

Pattern:

Observation: This looks like a square matrix. For the numbers, we can observe that numbers in each row are same, and are increasing if we go down a row.

Explanation: Size of the matrix is n*n. We will use a pair of nested loops to print this pattern. The outer loop and inner loop will iterate for n times each.

Here we want to print the row number in every row.Each row starts with the same number, which is equal to the row number—this is known as the row starts property in such patterns. We can do this by printing the value of 'i'.

Example 25 : Right Angled Triangle (Increasing column-wise)

Pattern:

Observation: This pattern looks similar to Example 25. The difference is that here we want to print the triangle. We can refer to Example 1 to do that.

You can refer Number Pattern Programs in Java to get a better understanding of different number pattern logics.

Explanation: We will print 'j' in every row, and we will bound j till i, as done in patterns before.

You can refer Number Pattern Programs in Java to get a better understanding of different number pattern logics.

Character Pattern Programs in Java

Character Pattern Programsin Java are very similar to Star Pattern Programs in Java, but they have sequences like Number Pattern Programs in Java.

A simple character problem would be to print the alphabet in Uppercase. We can easily do this, Just by knowing the ASCII code of 'A' and iterating till 'Z'.

ASCII codes:

• A-Z (Upper case) : 65 to 90.
• a-z (Lower case) : 97 to 122.
• ' ' (blank space) : 32

Each pattern program is typically implemented within a public class in Java, which provides the structure for the code.

We can use explicit type conversion to convert the ASCII values to characters.

Output:

Advanced Patterns

Advanced patterns in Java take your skills to the next level by combining multiple programming concepts such as nested loops, complex conditional statements, and mathematical logic. Examples of advanced patterns include Pascal’s Triangle, which uses binomial coefficients to print a triangle of numbers, Floyd’s Triangle, and the butterfly star pattern, which requires careful management of spaces and stars to achieve the desired effect.

Creating these patterns often involves using multiple levels of nested loops and intricate logic to control the placement of each element. For instance, the butterfly star pattern requires you to print stars and spaces in a mirrored fashion, while Pascal’s Triangle involves calculating and printing binomial coefficients for each row.

Mastering advanced patterns not only demonstrates your proficiency in Java programming but also sharpens your problem-solving skills, as you learn to break down complex requirements into manageable code using loops, conditional statements, and mathematical reasoning.