Radix Sort Program in C

Overview
Radix sort is a sorting algorithm that is used to arrange the elements of an array in a particular sorted order. It is a digit-by-digit sorting algorithm which makes it faster than most sorting algorithms including merge sort and quick sort as well. Radix sort program in C sorts the array in linear time but the data must be between a range of elements.
Introduction
Radix sort is a sorting algorithm that helps arrange elements of an array in a particular sorted order. Sorting makes searching and accessing data easier. Sorting is mostly used for numerical data or for arranging data in lexicographical order(i.e. dictionary order). It uses counting sort as a subroutine to sort.
Radix sort is a digit by digit sorting algorithm starting from the least significant (digit at the right-most position) to the most significant one(digit at the left-most position). It is a non-comparative algorithm which means it doesn't compare two elements of the same array to sort them. Thus, it is only applicable to arrays that contain elements in a certain range. This certain range is 1 to n^2^ where n is the number of elements in an array, to sort the array in linear time i.e. O(n) time complexity.
Radix sort takes the least significant digit of each of the elements and places them in the array in such a way that all the elements with the same least significant digits are placed together and elements having the least significant digit 0 are placed first, then the one having 1 are placed next and so on.
Similarly, the second least significant digit is considered and sorted. This process is performed as many times as the number of digits present in the maximum value of the array. Thus, it is a digit-by-digit sorting algorithm. Also, it is called non-comparative as we are not comparing any values of the arrays with other values that are present in the array.
If we observe the array below carefully we see that firstly the elements are sorted by the digits at the unit's place and then by the ten's place. Finally, we get the required array. This is roughly how the Radix sort program in C works.
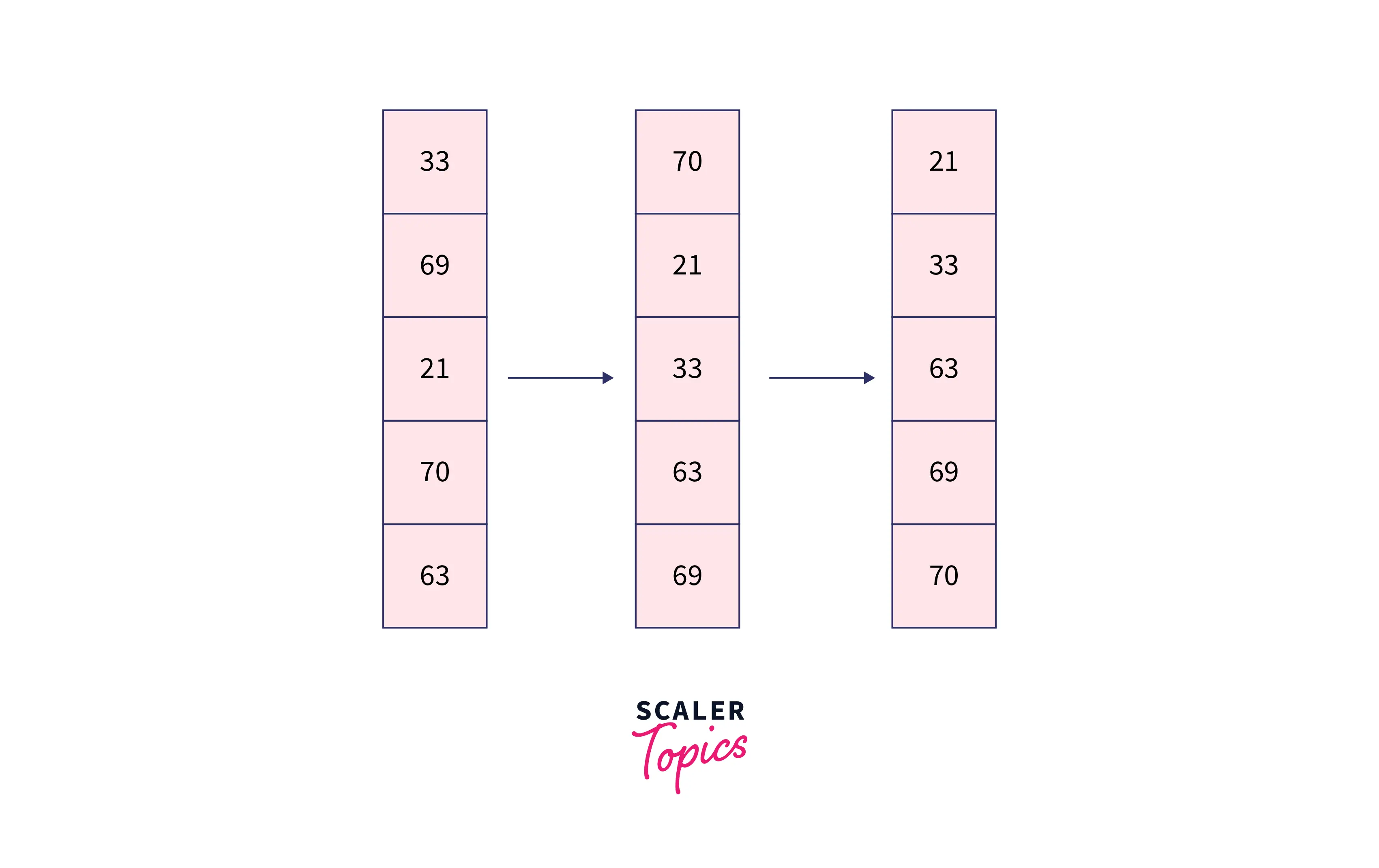
Algorithm of Radix sort
Let us look at the structured algorithm for the Radix Sort program in C.
Radix Sort
- Find the max value from the array say max. This will return the maximum number of digits and thus, the number of times we should run the loop and call CountSort say dts.
- Call CountSort dts times, pass the array, number of elements in the array i.e. n and exp. The value of exp is 1 in the first iteration and it is multiplied by 10 after each iteration.
Counting Sort
- Create two arrays count of size 10 and output of size the same as the array.
- Initialize count with 0.
- Perform count[(num[i]/exp)%10]++ for each element in the array using for loop. (We are counting the number of elements having the same value for a significant digit).
- Run a for loop, i ranging from 1 to 10, and perform count[i] = count[i-1]. This will return the index for elements to be placed.
- Lastly, run a for loop on the array i ranging from n-1 to 0 i.e. starting from behind. Find the value of num[i]/exp. Look for its value in the count array. Place the element in the output array at the index count[(num[i]/exp)%10]-1 and subtract 1 from count[(num[i]/exp)%10].
- Lastly copy each value of output into nums.
Working of Radix sort
To understand the working of Radix sort, let us look at the example of the array given below:
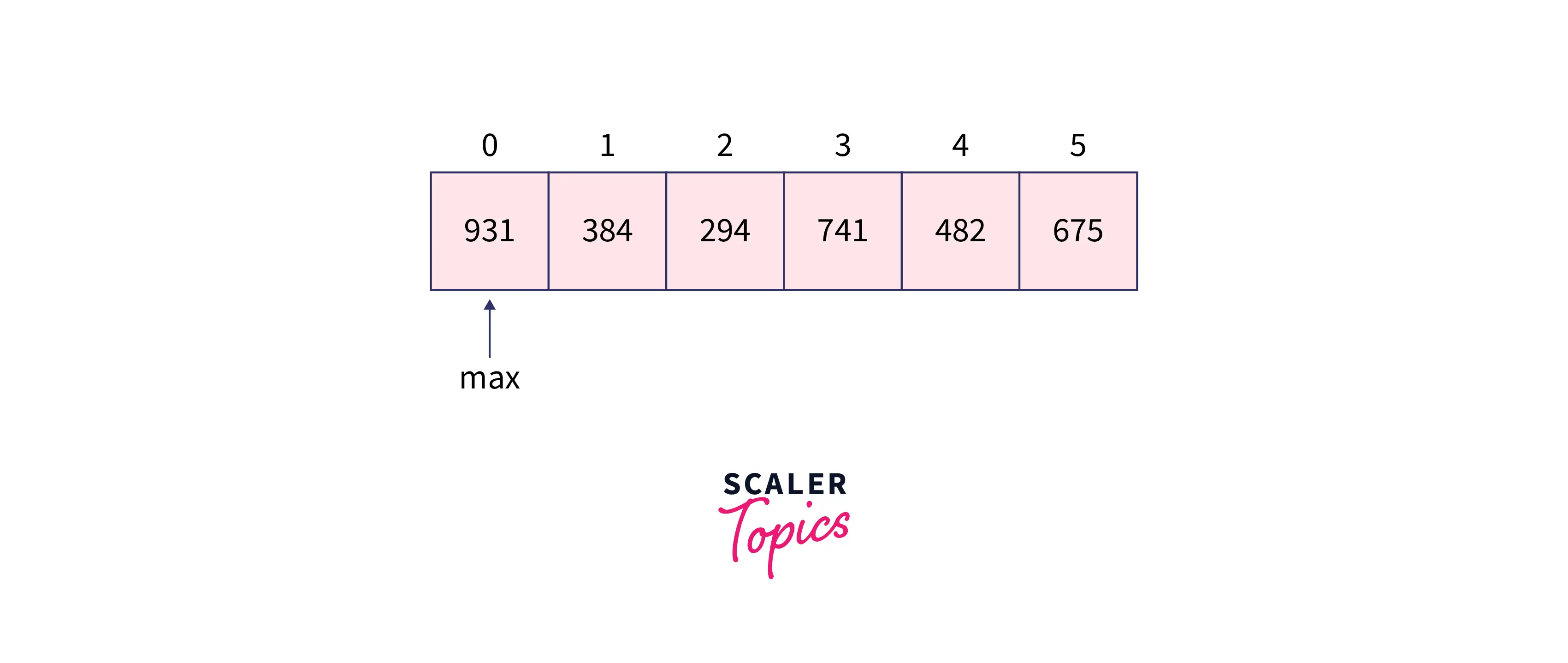
We first figure out the largest element in the array, in this case, it is 931. Next, we know it has 3 digits so we will be running a loop three times. The countSort function will be called with different values of exp. exp indicates the digit to be targeted to sort.
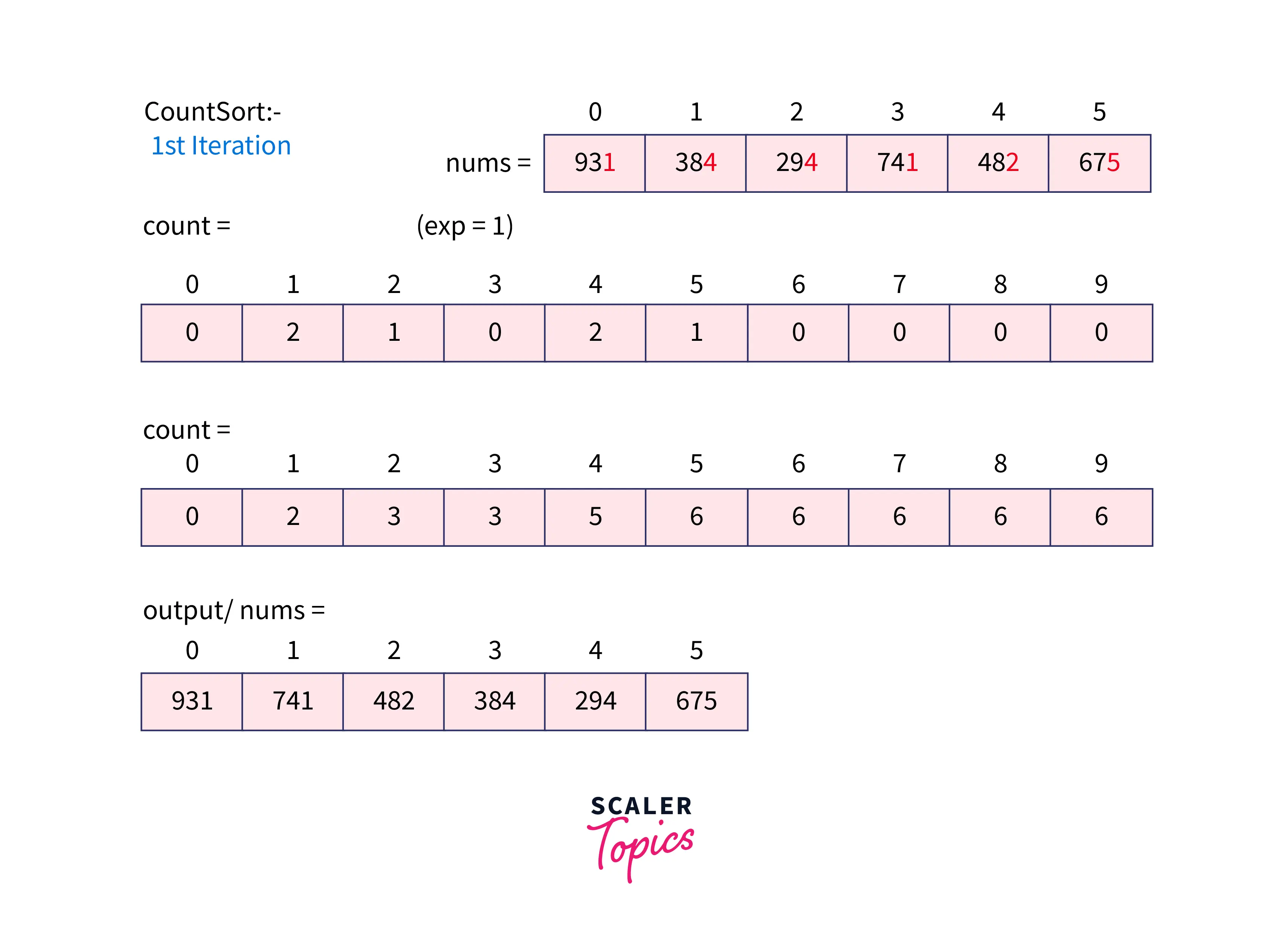
The value of exp is 1 and thus taking modulus with 10 it returns the rightmost digit to sort. We count all the elements having 0's at one's place, 1's at one's place, 2's at one's place, and so on.
Then we add all the elements sequentially i.e. count[i]=count[i]+count[i-1] to get the index just like a prefix sum.
Lastly, we form the output array using the count and the nums array. We visit each element of the nums array from (n-1)^th^ element to 0^th^ element i.e. we move from rightmost to leftmost element. We calculate the position of the element in the count array using the formula (nums[i] / exp) % 10. We read the value and subtract it by 1 in the count array. This value - 1 gives the index at which the element should be placed in the output array. Output is copied to the nums array.
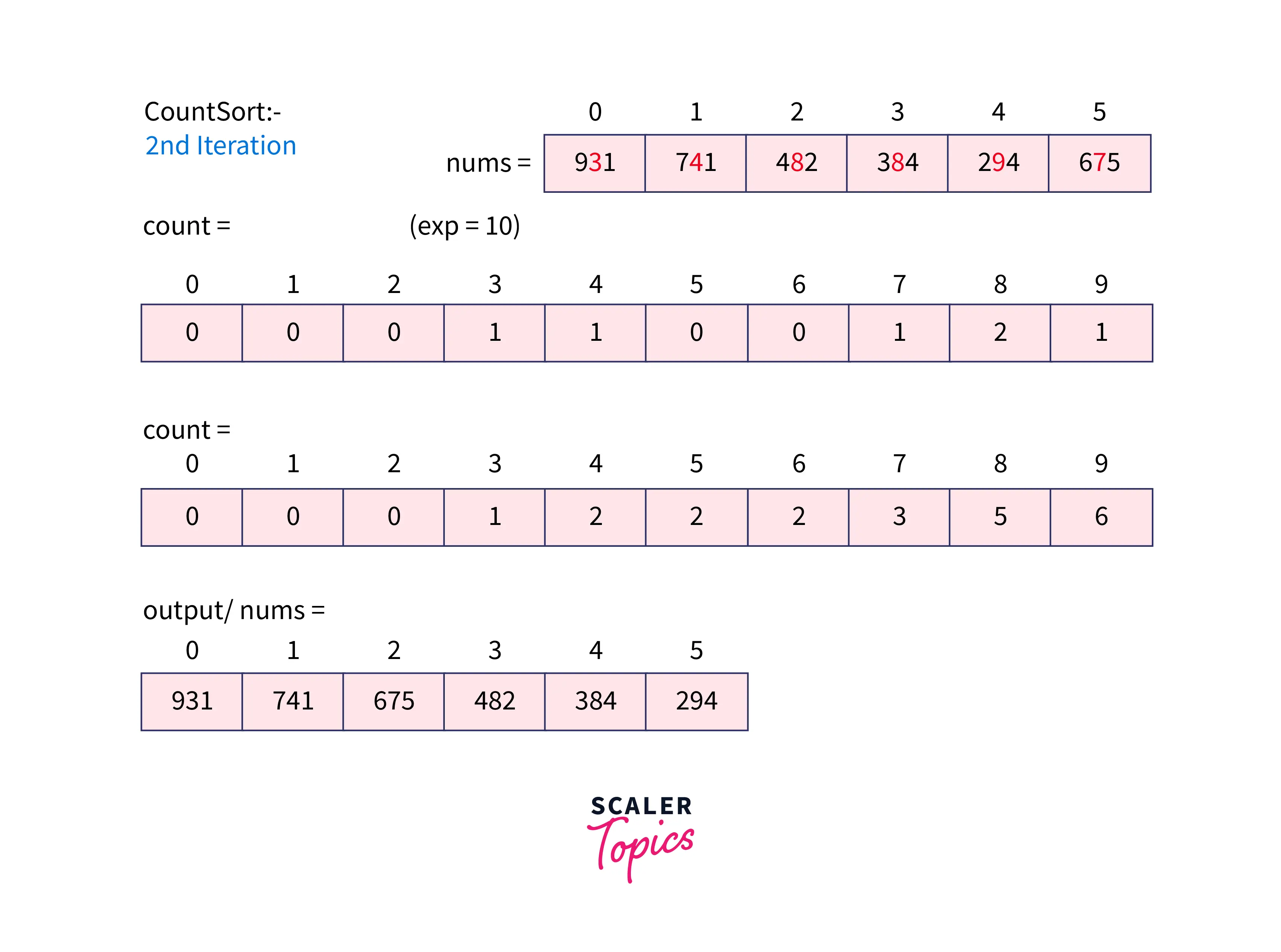
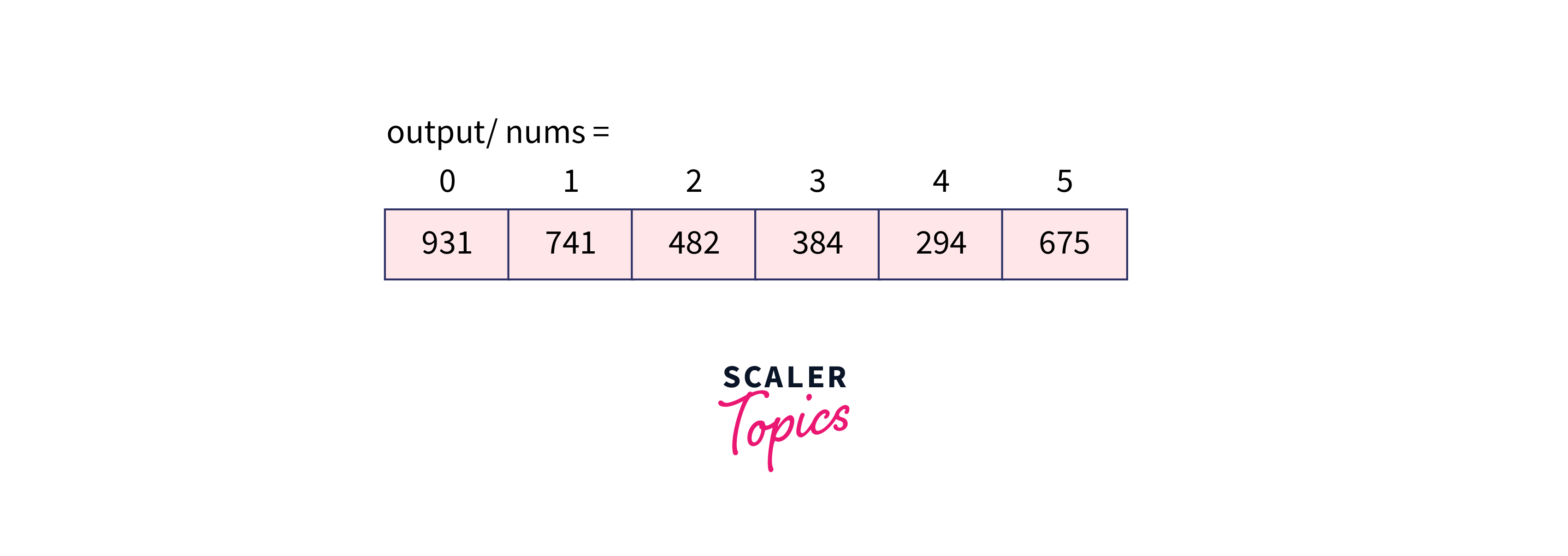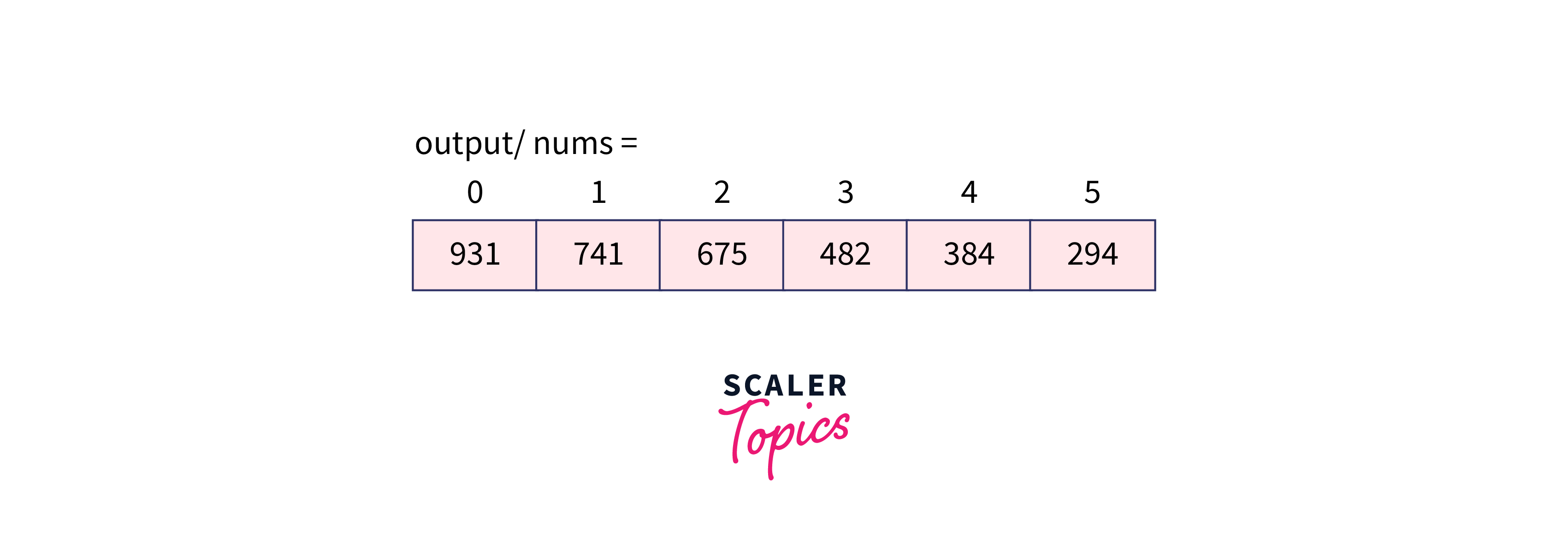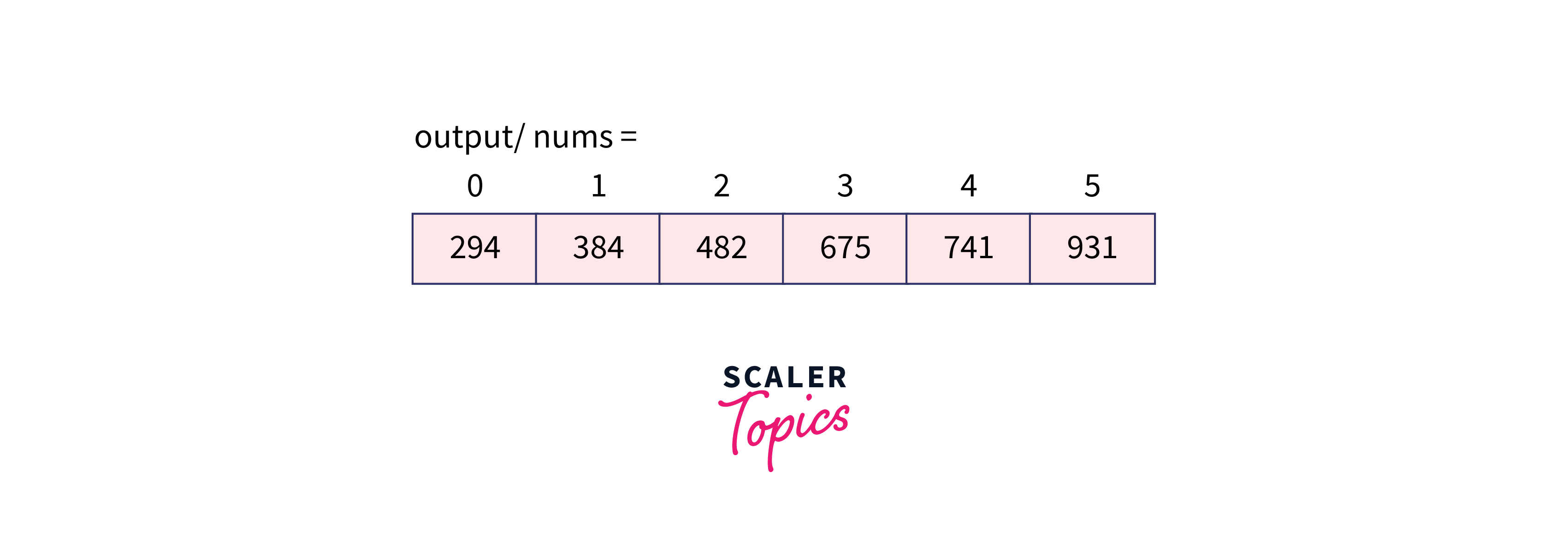
Now, exp becomes 10 and we follow the same process for the digit at the ten's position.
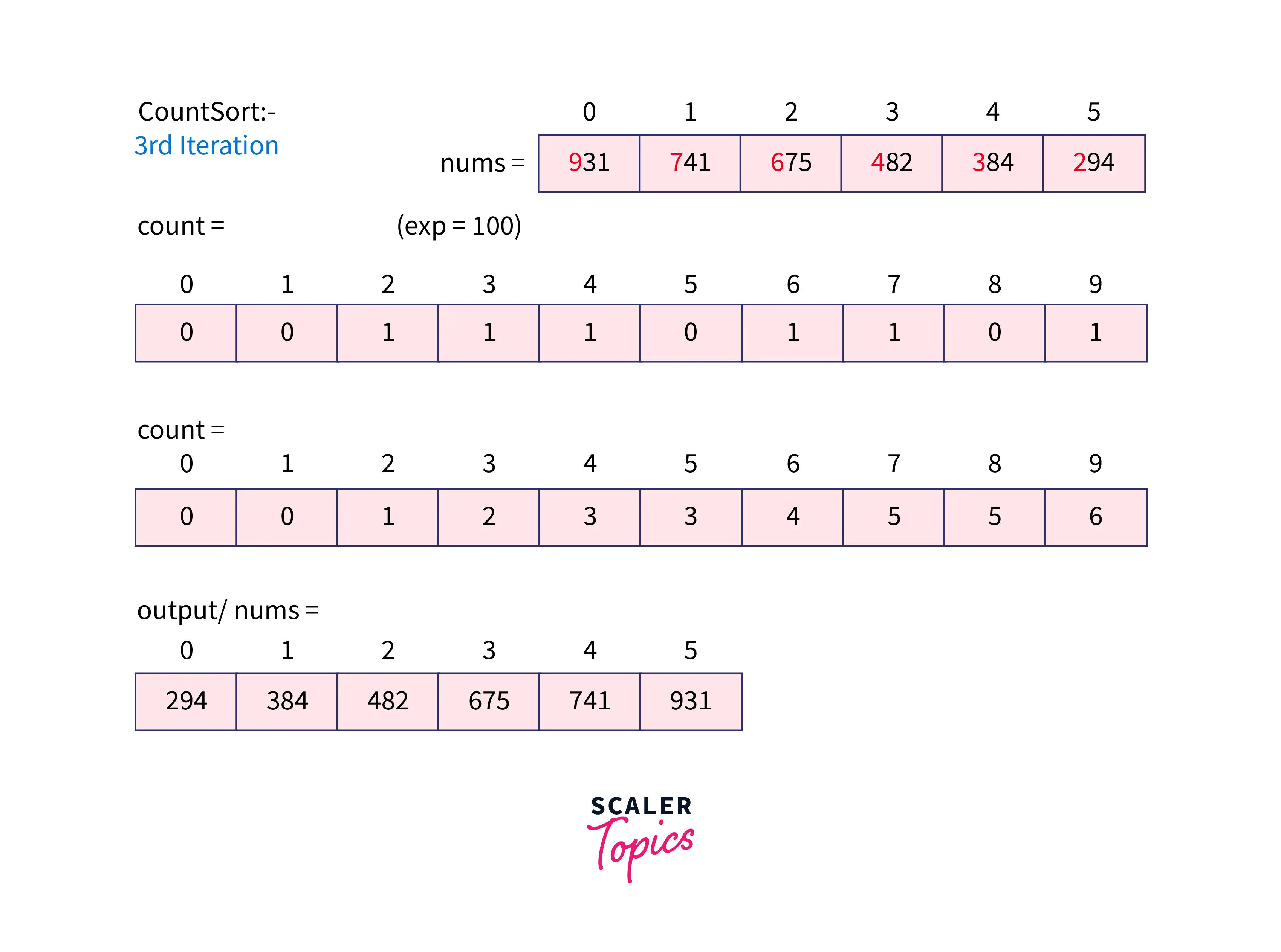
Again exp becomes 100 which is less than the max element and thus, we will call the CountSort function and it returns the sorted array.
Examples
Let us take another bit complex example having 1 digit 2 digits and 3-digit elements for the Radix sort algorithm. The example has 10 elements and the array is as follows:
| 783 | 91 | 20 | 443 | 579 | 931 | 812 | 0 | 581 | 366 |
|---|
As the maximum number has 3 digits the loop in RadixSort will run three times and call the CountSort function. After the first iteration, the array is as follows:
| 20 | 0 | 91 | 931 | 581 | 812 | 783 | 443 | 366 | 579 |
|---|
After 2nd iteration the array is as follows:
| 0 | 812 | 20 | 931 | 443 | 366 | 579 | 581 | 783 | 91 |
|---|
After 3rditeration the array is sorted and is given below:
| 0 | 20 | 91 | 366 | 443 | 579 | 581 | 783 | 812 | 931 |
|---|
Implementation of Radix sort in C
So to implement the Radix sort program in C we are required to create 4 functions. The first function getmax() returns the maximum value in the array. Then radix sort runs a for loop and provides the array and value of exp to the CountSort array. The print() function prints the array after sorting.
Output:
In the implementation above the getMax() method takes the array and its size as parameters and returns the maximum value present in the array. The RadixSort() function takes the array and its size as parameters and calls the getMax() method to get the max value which is used to run the for a loop. This for loop calls CountSort() method for each digit present in a max value.
CountSort() method takes the array, its size, and exp as parameters and sorts the array according to the value of exp. The value of exp tells the count sort digit at which position to choose and sort the array accordingly.
Radix sort complexity
Time Complexity
- Best case time complexity for the radix sort program in C is where n is the number of elements and k is the number of digits in the max value. It is when the array is already sorted.
- Average case time complexity is most useful where the values are neither sorted nor in descending order. Time complexity for the same is Θ(nk)(Theta(nk));
- The worst-case time complexity for the radix sort program is .
Space Complexity The extra space we use is in the count and output arrays which is equal to .
Conclusion
- Radix sort is a sorting algorithm that sorts the array in linear time.
- It is a digit by digit and non-comparative algorithm.
- Its time complexity is which is lesser than Quick sort and Merge sort algorithms.
- It uses the counting sort algorithm as its subroutine.
- Radix sort is only applicable for the data in the range 1 to n^2^.
