Random Forest in R Programming
Overview
Random Forest is an ensemble machine learning algorithm that combines multiple decision trees to enhance predictive accuracy and handle complex datasets. It mitigates overfitting by aggregating the predictions of individual trees, resulting in a versatile and powerful model suitable for classification and regression tasks.
What is Random Forest in R?
Random Forest is a popular machine learning algorithm used for both classification and regression tasks. It's particularly known for its versatility, robustness, and ability to handle complex datasets. In R, the Random Forest algorithm is implemented through the randomForest package, which provides functions to create and train Random Forest models.
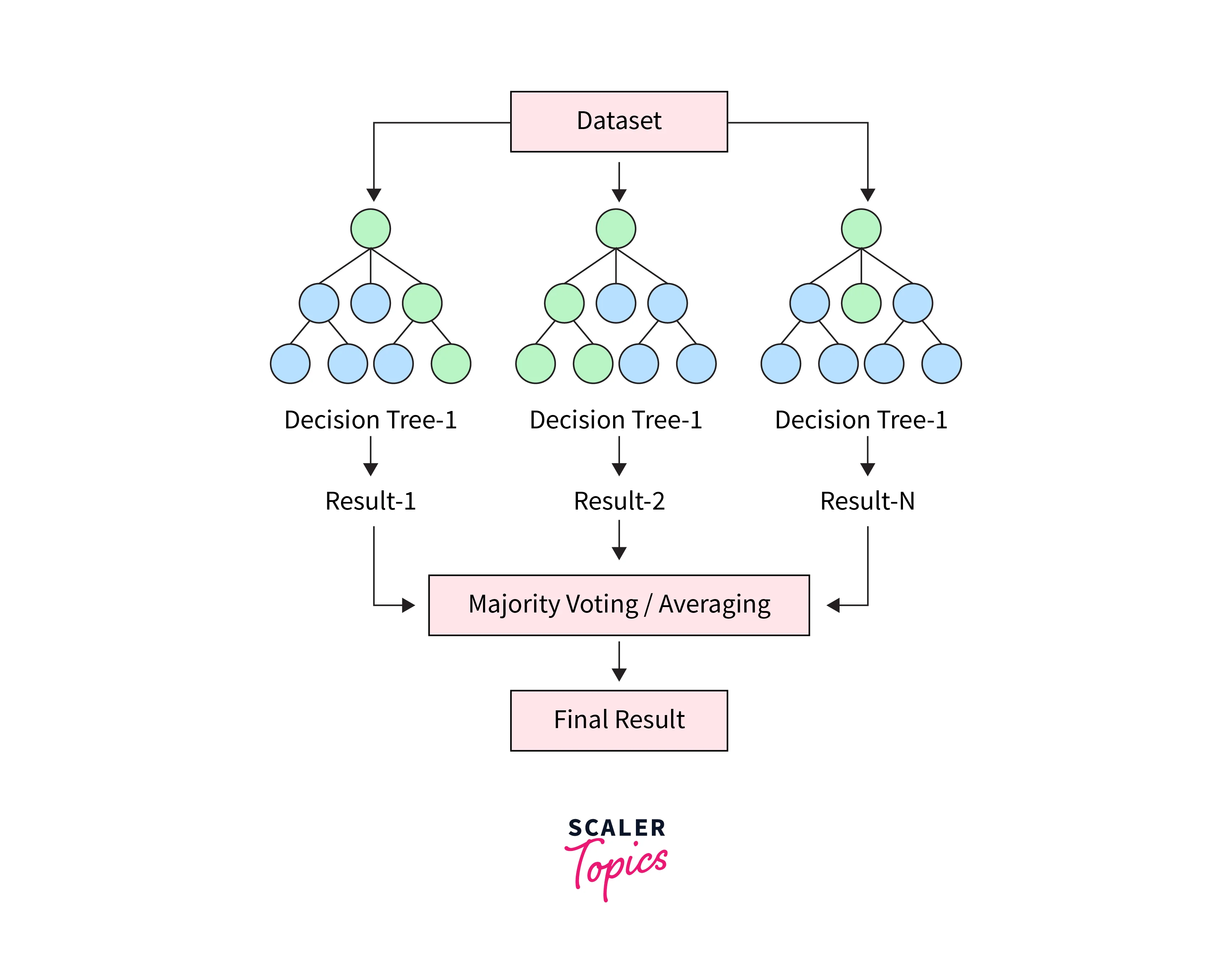
Here's a general overview of how Random Forest works:
-
Ensemble of Decision Trees: Random Forest builds an ensemble (a collection) of decision trees. Each tree is constructed using a subset of the training data and a random subset of features. These subsets are created using a process called "bagging" (Bootstrap Aggregating).
-
Random Feature Selection: At each node of a decision tree, a random subset of features is considered for making splits. This randomness helps to decorrelate the trees and reduces the risk of overfitting.
-
Voting or Averaging: For classification tasks, the mode (most frequent prediction) of the classes predicted by individual trees is taken as the final prediction. For regression tasks, the predictions from all trees are averaged to obtain the final prediction.
-
Reducing Variance: The main advantage of Random Forest is that it reduces overfitting by averaging the predictions of multiple trees. Each individual tree might overfit the data, but when combined, they tend to provide more stable and accurate predictions.
In R, you can use the randomForest package to create and train a Random Forest model. Here's a basic example of how to use it for a classification task:
Output
Remember to adjust parameters such as the number of trees, maximum depth of trees, and others based on your specific problem and dataset. The randomForest package provides many options for fine-tuning the algorithm's behavior.
Note that this example is simplified, and there are additional features and considerations when working with Random Forests in practice, such as handling missing values, optimizing hyperparameters, and evaluating model performance using techniques like cross-validation.
Decision Tree vs Random Forest
| Aspect | Decision Tree | Random Forest |
|---|---|---|
| Model Type | Single decision tree | Ensemble of decision trees |
| Complexity | Can be shallow or deep | Generally deeper for better performance |
| Bias-Variance Trade-off | High bias and low variance (shallow) | Balanced bias-variance trade-off |
| Interpretability | Highly interpretable path from root to leaf | Less interpretable due to ensemble |
| Overfitting | Prone to overfitting, especially when deep | Reduced overfitting due to aggregation |
| Robustness | Sensitive to noise and outliers | More robust due to ensemble and randomness |
| Generalization | Limited generalization to new data | Improved generalization through averaging |
| Sensitivity to Data | Highly sensitive to data variations | Less sensitive due to ensemble randomness |
| Computational Cost | Lower computational cost | Higher computational cost for ensemble |
Remember that the choice between Decision Trees and Random Forests depends on the specific characteristics of your problem, your data, and the trade-offs you are willing to make between interpretability and performance.
Random Forest Algorithm Features
The Random Forest algorithm offers several features that contribute to its effectiveness and popularity in machine learning applications. Here are some key features of the Random Forest algorithm:
-
Collective Grouping of Decision Trees: Random Forest operates as an ensemble learning technique, merging several decision trees to make predictions. This approach of combining trees enhances the accuracy of predictions and their generalizability.
-
Random Selection of Subsamples: The algorithm employs bootstrapped samples (randomly chosen samples with replacements) from the training dataset to create distinct datasets for each individual tree. This introduces variation and diversity into the data used for training each tree.
-
Haphazard Feature Choice: At each branching point of a decision tree, only a random subset of features is considered for the decision-making process. This random feature selection disassociates the trees and diminishes the risk of overfitting by preventing dominant features from exerting undue influence over all trees.
-
Majority Voting or Averaging: In the context of classification tasks, the final prediction results from a majority vote among the individual tree predictions. For regression tasks, the ultimate prediction is calculated as the mean of predictions from all the trees.
-
Combination of Bagging: The amalgamation of bootstrapped sampling and the averaging or voting process decreases variance and enhances model stability, thereby mitigating the likelihood of overfitting.
-
Out-of-Sample (OOS) Error: Since each tree is trained using a bootstrapped sample, the data left out of a particular tree's training set (out-of-bag samples) can be employed to assess the model's performance without necessitating an additional validation dataset.
-
Parallelization Capability: Because each tree in the ensemble can be independently trained, the training process can be parallelized, leading to quicker training times, especially on processors equipped with multiple cores.
-
Resilience to Perturbations: Compared to individual decision trees, Random Forest exhibits a decreased sensitivity to anomalies and noisy data due to the confluence of predictions from multiple trees.
-
Significance of Features: Random Forest offers a metric for gauging the importance of different features, revealing which features contribute more substantially to the model's predictions. This insight can be beneficial for feature selection and gaining insights into the data.
-
Management of Missing Data: Random Forest can manage missing data by employing surrogate splits during the construction of trees, reducing the necessity for pre-processing imputation techniques.
Overall, the Random Forest algorithm's combination of ensemble techniques, randomness, and inherent robustness makes it a powerful tool for building accurate and generalizable predictive models.
How Does a Random Forest Work?
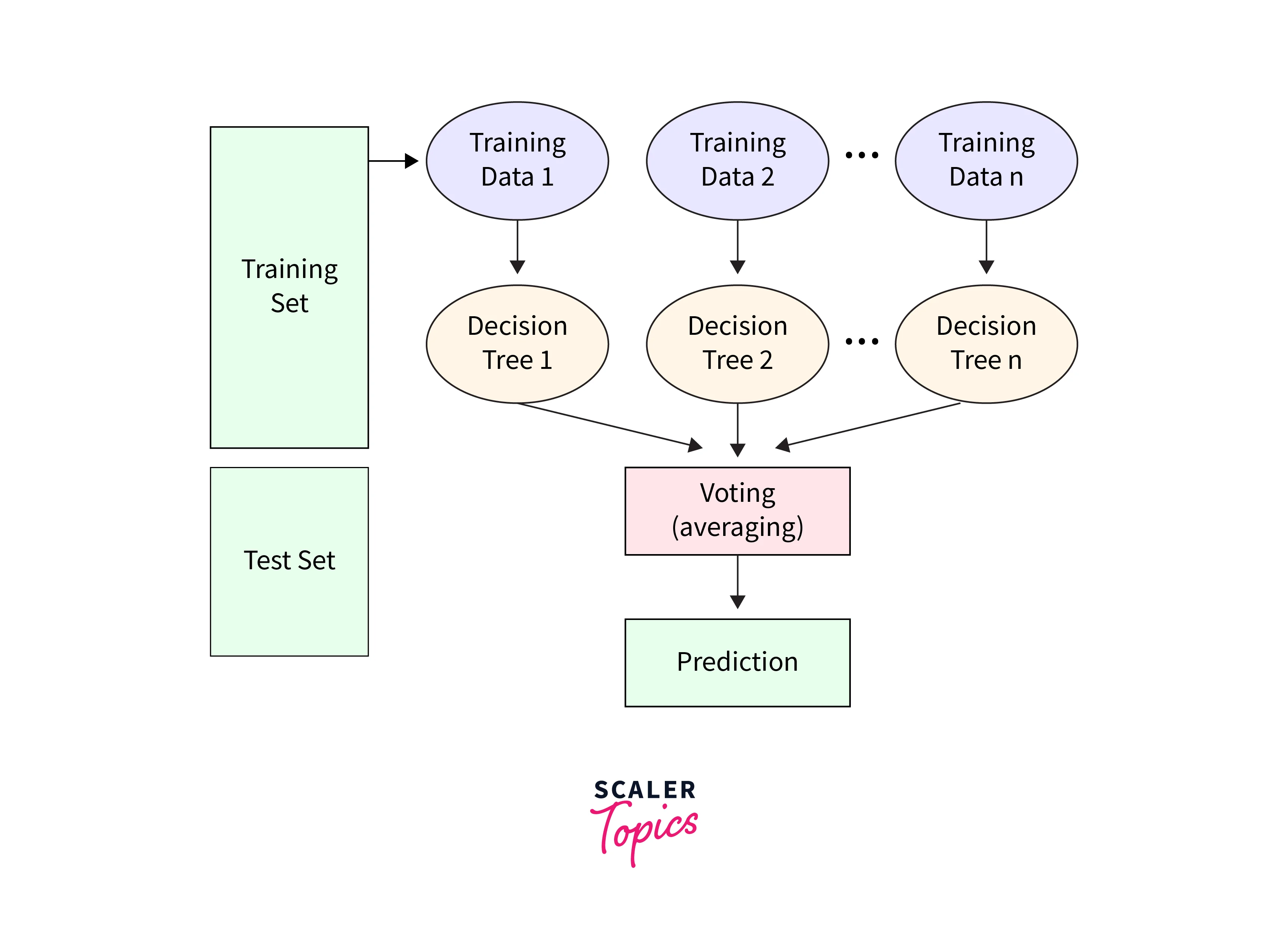
Random Forest functions as an ensemble learning method, merging predictions from numerous decision trees to craft a more precise and resilient model. Here's a sequential breakdown of Random Forest's operation::
-
Data Preparation:
- Random Forest is typically used for supervised learning tasks, both classification and regression.
- The training dataset is divided into features (input variables) and the target variable (output variable) that you want to predict.
-
Bootstrapped Sampling:
- For each tree in the forest, a random sample (with replacement) is drawn from the training dataset. This creates a "bootstrapped" sample for training that is slightly different for each tree.
-
Random Feature Selection:
- At each node of each tree, a random subset of features is selected to determine the best split. This prevents a single dominant feature from dictating the decision for many trees.
-
Tree Construction:
- Using the bootstrapped sample and the randomly selected features, a decision tree is constructed through a process of recursive binary splitting. The tree is grown until a stopping criterion is met, such as reaching a maximum depth or a minimum number of samples in a leaf node.
-
Voting or Averaging Predictions:
- For classification tasks, each tree's prediction is based on the majority class of the samples in the corresponding leaf node. The final prediction is determined by majority voting among all the trees' predictions.
- For regression tasks, each tree predicts a numerical value for the target variable in the leaf node. The final prediction is the average of the predictions from all the trees.
-
Aggregation and Output:
- Once all the trees have made their predictions, the Random Forest algorithm aggregates the individual predictions to make a final prediction. The method of aggregation depends on the task (classification or regression).
-
Out-of-Bag (OOB) Evaluation:
- As each tree is trained using a bootstrapped sample, the information excluded from a specific tree's training set (known as out-of-bag samples) can be utilized to gauge the model's performance. This offers an intrinsic validation approach, eliminating the requirement for a distinct validation dataset.
-
Feature Importance:
- Random Forest provides a measure of feature importance based on how much each feature contributes to reducing impurity in the trees. Features that are frequently chosen for splits at higher levels of the trees are considered more important.
-
Prediction and Evaluation:
- Once the Random Forest model is trained, it can be used to make predictions on new, unseen data. The aggregated predictions from the ensemble of trees provide more accurate and robust predictions compared to a single decision tree.
In summary, Random Forest leverages the principles of ensemble learning, bootstrapped sampling, and random feature selection to create a collection of decision trees that work together to improve prediction accuracy, reduce overfitting, and handle noisy data. The algorithm's ability to harness the power of multiple trees while reducing individual trees' biases and variance makes it a powerful tool for various machine learning tasks.
Preparing Dataset for Random Forest
Preparing your dataset for use with the Random Forest algorithm involves several steps to ensure that your data is in the right format and quality. Here's a guide to preparing your dataset for Random Forest:
-
Data Cleaning:
- Address missing values: Decide on a strategy for handling missing values, such as imputation or removing rows/columns with missing values.
- Remove duplicates: Check for and eliminate any duplicate rows in your dataset.
- Handle outliers: Determine whether outliers need to be addressed, as Random Forests are generally less sensitive to outliers compared to single decision trees.
-
Feature Selection and Engineering:
- Identify relevant features: Analyze your dataset to select the most relevant features that contribute to the target variable. Discard irrelevant or redundant features.
- Create new features: Consider generating new features that might capture important information, like interactions between existing features or domain-specific transformations.
-
Categorical Variables:
- Convert categorical variables: Convert categorical variables into numerical format using techniques like one-hot encoding or label encoding. This ensures that the algorithm can process them properly.
-
Data Splitting:
- Split the dataset: Divide your dataset into training and testing sets. This allows you to train the model on one portion and evaluate its performance on another, unseen portion.
-
Feature Scaling:
- Normalize or standardize features: Depending on the nature of your features and the algorithm's sensitivity to feature scales, consider scaling your features to a similar range. Random Forest is not as sensitive to feature scaling as some other algorithms, but scaling can still help in some cases.
-
Handling Imbalanced Classes (for Classification):
- If your classification problem has imbalanced classes, consider techniques like oversampling, undersampling, or using appropriate evaluation metrics to account for class imbalance.
-
Parameter Tuning:
- While Random Forest has fewer hyperparameters to tune compared to some other algorithms, you may still need to experiment with parameters like the number of trees, maximum depth, minimum samples per leaf, etc., to achieve optimal performance.
-
Out-of-Bag (OOB) Evaluation:
- Keep in mind that Random Forest offers an internal validation mechanism through the out-of-bag (OOB) samples. This can help you assess the model's performance during training without a separate validation set.
-
Handling Multicollinearity:
- If your dataset has high multicollinearity (correlation between predictor variables), it might affect the performance and interpretability of the model. Consider addressing this issue by applying dimensionality reduction techniques or feature selection.
Output
Terminologies in the Random Forest Algorithm
Terminologies in the Random Forest Algorithm:
-
Ensemble Learning: The practice of amalgamating multiple models, often decision trees, to construct a more potent and precise predictive model.
-
Decision Trees: Fundamental elements of the Random Forest algorithm, forming tree-like structures that use recursive feature value splits to predict target outcomes.
-
Bootstrapped Sampling: The process of randomly selecting data samples from the training set with replacement, generating diverse subsets for individual trees.
-
Random Subspace: Feature bagging or random subspace involves picking a random subset of features for each tree, introducing variation and diversity into feature selection.
-
Voting or Averaging: In the Random Forest ensemble, predictions of individual decision trees are combined through either majority voting (for classification) or averaging (for regression) to determine the final prediction.
-
Bagging (Bootstrap Aggregating): A technique where each decision tree is trained on a bootstrapped sample, and their aggregated predictions enhance model accuracy and robustness.
-
Feature Importance: Random Forest assesses feature importance by measuring contributions to predictions. Features with higher importance values play more significant roles.
-
Gini Impurity: A measure of randomness within a sample set, utilized for guiding tree-building through optimal split selection.
-
Entropy: A measure of disorder within samples, used to determine splits in decision tree algorithms.
Performing Random Forest on Dataset
Let's perform a Random Forest analysis on a dataset. For this example, we'll use the "Boston Housing" dataset from the MASS package, which contains information about housing prices in Boston. We'll perform a regression task to predict the median value of owner-occupied homes.
Here's how you can do it in R:
Output
In this example:
- We load the required libraries: randomForest for the Random Forest algorithm and MASS for the Boston Housing dataset.
- We load the Boston Housing dataset and inspect its structure using str() to understand its contents.
- We split the dataset into features (X) and the target variable (y).
- We split the data into training and testing sets using a random sample of 70% for training and 30% for testing.
- We train a Random Forest model using the training data (X_train and y_train).
- We make predictions on the test set (X_test) using the trained model.
- We calculate the Mean Squared Error (MSE) to evaluate the model's performance.
Replace the "Boston Housing" dataset with your own dataset and adjust the code accordingly to perform Random Forest analysis on different data.
Shortcomings of Random Forest
While Random Forest is a powerful and versatile algorithm, it's important to be aware of its limitations and potential shortcomings:
-
Computational Complexity: Random Forest can be computationally intensive, especially with a large number of trees and complex datasets. Training and evaluating a large ensemble of trees can require substantial computational resources.
-
Model Interpretability: While individual decision trees are relatively easy to interpret, the ensemble nature of Random Forest can make it more challenging to explain the combined decision-making process of the entire forest.
-
Memory Usage: Storing multiple decision trees and associated data can consume significant memory, especially for large datasets or when using a high number of trees.
-
Bias in Feature Importance: Random Forest's feature importance measures can sometimes be biased in favor of variables with high cardinality (many unique values) or continuous variables with more splits. This can affect the accuracy of importance rankings.
-
Overfitting with Noisy Data: While Random Forest is less prone to overfitting than individual decision trees, it can still struggle with noisy data if the noise is not properly managed during preprocessing.
-
Limited Extrapolation: Random Forest can't extrapolate well beyond the range of training data. If the test data falls outside the range of the training data, predictions may be less accurate.
It's important to consider these limitations when deciding whether to use Random Forest for a particular task and to carefully preprocess data, tune hyperparameters, and evaluate model performance to ensure the algorithm's effectiveness.
Fine Tuning Random Forest
Fine-tuning a Random Forest model involves adjusting its hyperparameters to optimize its performance for a specific problem. Validation datasets are crucial for tuning as they help select optimal parameters by gauging model performance on unseen data. Cross-validation enhances robustness by systematically rotating validation sets, providing a comprehensive assessment of parameter configurations' generalizability. Here's a small list on how to perform fine-tuning for a Random Forest model:
-
Select Hyperparameters to Tune: Identify the hyperparameters that have the most impact on the model's performance. Some key hyperparameters in Random Forest include:
- n_estimators: The number of trees in the forest.
- max_depth: The maximum depth of individual trees.
- min_samples_split: The minimum number of samples required to split an internal node.
- min_samples_leaf: The minimum number of samples required to be at a leaf node.
- max_features: The number of features to consider for the best split at each node.
-
Set Up Parameter Grid: Define a grid of values for the selected hyperparameters. You can create different combinations of hyperparameter values to search for the optimal configuration.
-
Cross-Validation: Split your training data into multiple folds and perform cross-validation. Cross-validation helps evaluate the model's performance across different subsets of the data, preventing overfitting to a specific subset.
-
Hyperparameter Search: Use techniques like grid search or randomized search to explore different combinations of hyperparameters. Grid search exhaustively tries all possible combinations from the defined parameter grid, while randomized search samples a fixed number of combinations randomly.
-
Evaluation Metric: Choose an appropriate evaluation metric based on your problem. For regression, you might use Mean Squared Error (MSE), while for classification, metrics like accuracy, F1-score, or area under the ROC curve (AUC-ROC) are common.
-
Model Training and Evaluation: For each combination of hyperparameters, train the Random Forest model on the training data using k-fold cross-validation. Evaluate its performance on the validation folds using the chosen evaluation metric.
-
Select Best Hyperparameters: Choose the set of hyperparameters that yields the best performance on the validation data. This is often referred to as the "best" configuration for your Random Forest model.
-
Final Model Evaluation: After finding the best hyperparameters, train a final Random Forest model using these settings on the entire training dataset. Evaluate its performance on an independent test dataset that hasn't been used for hyperparameter tuning.
-
Interpretability and Generalization: Remember that while fine-tuning can improve model performance, it's essential to strike a balance between optimization and model interpretability. Avoid overfitting to the validation data and ensure that the model generalizes well to new, unseen data.
-
Automated Tools: Consider using automated hyperparameter tuning libraries like caret or scikit-learn's GridSearchCV and RandomizedSearchCV for efficient hyperparameter search.
Fine-tuning Random Forest requires experimentation, patience, and a thorough understanding of your data and problem domain. It's crucial to strike a balance between complexity and performance to achieve the best results.
Random Forest Applications
-
Healthcare Diagnosis Random Forest is commonly employed in healthcare to diagnose diseases based on patient data and symptoms. It helps identify conditions such as cancer, heart disease, and diabetes by analyzing risk factors and medical history.
-
Credit Risk Evaluation Random Forest is used in finance to evaluate credit risk by forecasting the likelihood of loan defaults. It assesses financial attributes and repayment history to classify applicants as low or high credit risks, enhancing risk assessment accuracy.
-
Satellite Data Analysis Random Forest is applied in environmental monitoring and agriculture to analyze remote sensing data like satellite images. It categorizes land cover, detects deforestation, and forecasts crop yields, showcasing its ability to handle intricate spatial data.
-
Customer Analysis in Retail Retail utilizes Random Forest for customer segmentation, fraud detection, and recommendations. It uses customer behavior and demographics to group customers, identify fraud, and suggest tailored product recommendations.
Conclusion
- Random Forest is an ensemble machine learning algorithm that combines multiple decision trees to increase accuracy and handle complex datasets. It is effective in both classification and regression tasks
- In R, Random Forest is executed using the randomForest package. It involves creating decision trees on different data subsets and feature sets, with predictions aggregated through voting or averaging.
- Random Forest employs bootstrapped sampling and random feature selection, enhancing model robustness and reducing overfitting. It's highly effective due to its ensemble approach, voting/averaging mechanisms, feature importance evaluation, and out-of-bag error estimation for internal validation.
- Preparing data for Random Forest includes data cleaning, feature engineering, and handling categorical variables. Fine-tuning involves adjusting hyperparameters like the number of trees and maximum tree depth, often using cross-validation for robust parameter selection.
- Widely applied in fields like healthcare, finance, and environmental monitoring, Random Forest has limitations like computational intensity, reduced interpretability due to ensemble complexity, and potential bias in feature importance measures.
