Recursive Functions in R

Introduction

Recursion is a powerful concept wherein a function calls itself to solve a problem in smaller and more manageable pieces. It's like a Russian nesting doll of code, each layer peeling back to reveal a smaller version of the original problem. Recursive functions can be harnessed in R to write clean, efficient code that tackles complex tasks gracefully and precisely. Whether you're a novice exploring the depths of R or a seasoned programmer seeking to deepen your understanding, this guide will illuminate the elegant dance of recursion, enhancing your problem-solving skills. Let's begin our journey.

Understanding Recursion in Programming

Recursion is a concept common across various programming languages, including R. Before we delve into the specifics of recursive functions in R, it's important to understand the general idea of recursion in programming.

How Recursion Works

Recursion in programming is a method where a function calls itself to solve a problem. The function will continue to call itself until a condition known as the base case is met. Once the base case is achieved, the function stops calling itself and begins to return the results, unwinding the chain of function calls.

To illustrate, imagine that you're standing at the top of a staircase, and you want to reach the bottom. Each step you take down the staircase is analogous to a recursive call. You keep taking steps (recursive calls) until you reach the bottom (base case). Once you're at the bottom, you've completed your task and no longer need to take more steps (no more recursive calls).

Here's what a general recursive function might look like:

In this structure, the recursiveFunction continues to call itself with a progressively smaller problem until it reaches the base case. At this point, the function can start returning results up the chain. This process is known as 'unwinding' the recursion.

Advantages and Limitations of Recursion

Recursion offers several advantages and, at the same time, comes with certain limitations.

Advantages of Recursion:

1. Simplicity:

   Recursive functions can make the code look clean and elegant. They break down complex problems into simpler sub-problems, which can often be easier to understand and solve.

2. Reduction of unnecessary variables:

   With recursion, temporary variables can often be eliminated, making the code more efficient and readable.

3. Problem-solving approach:

   Recursion embodies a problem-solving paradigm called "divide and conquer." Breaking the problem into smaller pieces provides a clear and intuitive approach to tackling tasks that may otherwise be difficult to solve iteratively.

Limitations of Recursion:

1. Stack Overflow:

   Every time a recursive function calls itself, it pushes another layer onto the 'call stack.' If the recursion is too deep, i.e., the function calls itself too many times before reaching the base case, it can lead to a stack overflow error, causing the program to crash.

2. Performance:

   Recursive functions can be slower and consume more memory than their iterative counterparts, as they require memory allocation for each recursive call.

3. Complexity:

   While recursion can simplify some problems, it can also add complexity, especially for those unfamiliar with the concept. Understanding the flow of recursive functions can sometimes be challenging, making the code harder to debug and maintain.

Basic Concepts of Recursive Functions

Before implementing a recursive function, it's vital to understand its fundamental concepts: the base case, recursive case, and the design of recursive algorithms.

Base Case

The base case is the condition that stops the function from making further recursive calls. It is the simplest case that can be solved directly without recursion. Without a well-defined base case, a recursive function could keep calling itself indefinitely, leading to a stack overflow error. Identifying a suitable base case that the function will eventually reach is important, thereby halting the recursion.

Recursive Case

The recursive case is where the function calls itself, each time with a smaller or simpler input. It is designed so that each recursive call brings the function one step closer to the base case. This case is essentially the problem, broken down into simpler, smaller parts.

Recursive Algorithm Design

The design of a recursive algorithm generally follows these steps:

1. Identify the base case:

   Define the simplest form of the problem that can be solved directly.

2. Break down the problem:

   Divide the larger problem into smaller, simpler subproblems that are instances of the same problem.

3. Solve the subproblems:

   Use recursive calls to solve these smaller subproblems. Ensure that each recursive call brings the algorithm closer to the base case.

4. Combine the results:

   Once the base case is reached, start unwinding the recursion by combining the results from each recursive call to solve the overall problem.

Now that we understand the basic concepts of recursive functions, let's move on to implementing these concepts in R programming.

Recursive Functions in R

Like other programming languages, we can create recursive functions in R to handle complex tasks easily and efficiently. R's inherent ability to manipulate data structures combined with the power of recursion can lead to profound solutions to challenging problems. However, it's essential to use recursion judiciously to avoid performance pitfalls and maintain readability.

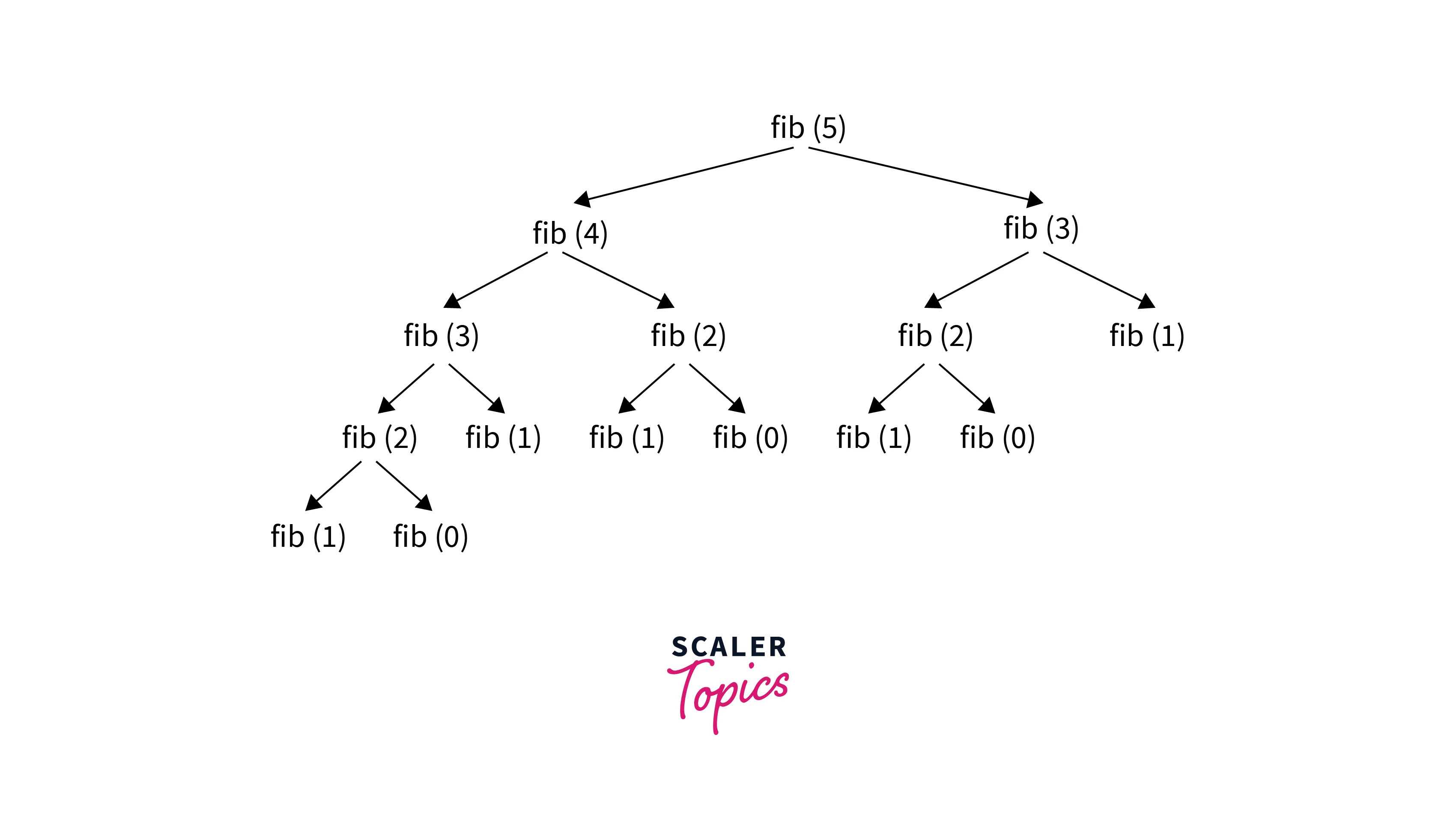
We'll create a recursive function to calculate the Fibonacci sequence, another common use case for recursion.

In the Fibonacci sequence, each number is the sum of the two preceding ones, usually starting with 0 and 1. In this recursive function, the base case is when n is less than or equal to 1. For these cases, the function directly returns n. The recursive case is when n is greater than 1. For this case, the function calls itself twice: once with n-1 and once with n-2, returning the sum of these two recursive calls.

Each call of fibonacci(n-1) and fibonacci(n-2) makes the problem smaller, bringing it closer to the base case. Once the base case is reached, the recursion starts unwinding, with each level of recursion returning a result to the level above, ultimately calculating the nth number in the Fibonacci sequence.

Example - Factorial Using Recursion in R

The factorial of a non-negative integer n is the product of all positive integers less than or equal to n. It's denoted by n!, a classic example of a problem that recursion can solve elegantly.

Let's create a recursive function in R to calculate the factorial of a number:

In this recursive function, the base case is when n equals 0. In this case, the function directly returns 1 because the factorial of 0 is 1. The recursive case is when n is greater than 0. Here, the function calls itself with n-1 and multiplies n by the result of this recursive call.

Each call of factorial(n-1) makes the problem smaller, bringing it closer to the base case. Once the base case is reached, the recursion starts unwinding, with each level of recursion returning a result to the level above, ultimately calculating the factorial of the number.

Example - Sum of Series Using Recursion in R

Let's consider another interesting example where we use recursion to calculate the sum of a numerical series in R. For instance, we may want to calculate the sum of the first n natural numbers.

Here's how we can do this using a recursive function:

In this recursive function, the base case is when n equals 1. For this case, the function directly returns 1. The recursive case is when n is greater than 1. Here, the function calls itself with n-1 and adds n to the result of this recursive call.

Each call of sumSeries(n-1) reduces the problem size, inching it closer to the base case. Once the base case is reached, the recursion starts unwinding, with each level of recursion returning a result to the level above, ultimately calculating the sum of the first n natural numbers.

Key Features of Recursion in R

1. Simplicity:

   Recursion in R can simplify the implementation of complex tasks by breaking them down into simpler sub-problems.

2. No Loop Constructs:

   Recursive functions often remove the need for traditional loop constructs, leading to cleaner code.

3. Efficiency:

   Recursion can be more memory efficient if it replaces a large amount of intermediate state that would otherwise be kept in loop variables.

4. Stack Overflow Risk:

   Deep recursion in R may lead to a stack overflow error if it exceeds the limit of recursive calls, necessitating effective base cases.

5. Problem-solving Approach:

   Recursion embodies the "divide and conquer" approach, providing a clear strategy for solving complex problems.

Applications of Recursion in R

Recursion finds numerous applications in R programming, simplifying complex problems into manageable tasks. Here are a few examples:

1. Data Structures:

   Recursive functions can traverse complex data structures such as lists, trees, and graphs. They can help perform operations like searching, sorting, or traversing each element.

2. Mathematical Computations:

   Recursion is commonly used to solve mathematical problems like calculating factorial, Fibonacci sequence, sum of series, etc.

3. Algorithm Design:

   Recursion is at the heart of several algorithmic paradigms, like 'divide and conquer' or 'dynamic programming.' Algorithms like quicksort, mergesort, tree-based algorithms, etc., often use recursion.

4. Nested or Hierarchical Data:

   Recursive functions can process and analyze nested or hierarchical data, common in fields like genomics, psychometrics, and network analysis.

5. Problem Simplification:

   Many complex problems can be simplified using recursion, breaking them into simpler, smaller subproblems.

Types of Recursion in R

Recursion in R and other programming languages can be generally classified into direct and indirect.

1. Direct Recursion:

   A function directly calls itself to perform a task in direct recursion. Most examples we've discussed, such as calculating factorial or the sum of a series, involve direct recursion. The function makes a call to itself within its own function body, reducing the problem's size with each recursive call.

2. Indirect Recursion:

   In indirect recursion, a function calls another function, which calls the first function. This type of recursion involves at least two functions circularly calling each other. It can be harder to understand and less common than direct recursion.