Recursively Remove All Adjacent Duplicates

Problem Statement

Given a string, remove all adjacent duplicates from the strings using recursion. Return the modified input string such that the it does not contain any adjacent duplicate characters.

Example

Example 1: For a better understanding of the problem statement let's have a look at the below mentioned example:

Input:

string str= "bbcedde"

Output:

"c"

Example Explanation

Firstly, the given input string is "bbcedde", remove all the adjacent duplicates initially, then the string becomes "cee". Here we need to remove all the adjacent duplicates again then the string becomes "c". Since in the present string, there are no adjacent duplicates present so we simply return the modified string as the output. It can be explained using the below image:

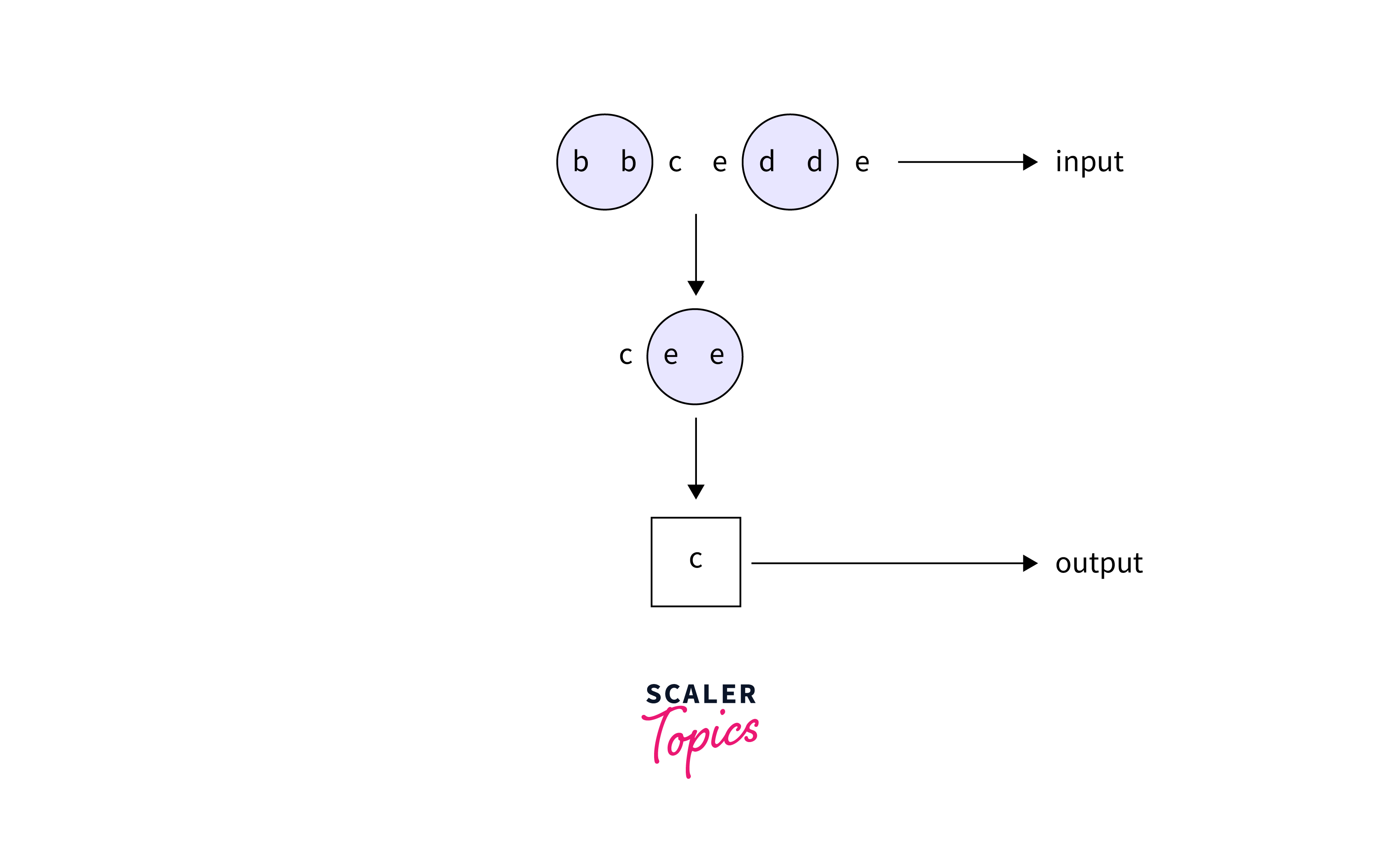
Input Format

Input format includes, for every test case a string given of length N.

Output Format

We need to return the output string which does not contain any adjacent duplicates. This string can be empty as well.

Constraints

• 1 <= N (length of the input string) <= 10^5
• Input string always contains lower case alphabets.

Approach 1: Using Schlemiel Painter’s Algorithm

The idea here is to use recursion for removing all the adjacent duplicates. In this approach we use Schlemiel painter's algorithm which is a class of procedures known as Schlemiel the Painter's Algorithm, also written as Shlemiel, states that many functions may appear to perform well under smaller workloads but when it comes to huge load they end up being very inefficient because of many redundant operations that are to be carried out to perform a task at a lower level. So, in this approach, we traverse the string from the leftmost end, the answer is always present at the remaining string variable assumed during recursion this remaining string has all the characters with no adjacent duplicates in it. Now, append the first character of the string with the remaining string and we need to call the recursive function for the next N-1 characters of the original string (where N is the length of the input string). And for every recursive call, we have to check whether the remaining string's last character is matching with the string which is passed through the recursion(also called as original string). For every recursive call, we check for the three possibilities which are first character of the remaining string can be same as the first character of input string, remaining string can become empty and the last removed character is the same as the first character of the string passed through the recursion or the third possibility can be just appending the first character of the string passed(original string) at the beginning of the remaining string . In this way, recursion is called for every small part of the string and we it helps in removing all the adjacent duplicates from the input string.

Algorithm

Below algorithm clearly explains the above approach:

• Firstly start traversing the input string from the left side.
• Include the leftmost character in the remaining_str, now the recursive function by passing the string of size (N-1) i.e, from the second character.
• For every recursive call we need to check for the below three possibilities:
  • The first possibility can be the first character of the remaining string is the same as the first character of the string which is passed through the recursion, If this is the possibility then we need to remove the first character from the remaining string. This is achieved using a while loop.
  • The second possibility is if the remaining string becomes empty and the last removed character is the same as the first character of the string passed through the recursion. In this case, we need to return the empty string. As there are no distinct adjacents present in the given string.
  • The last possibility is nothing of the above two cases happened then we just need to append the first character of the string passed(original string) at the beginning of the remaining string.
• At any point in the recursion, we need to keep track of the last removed character and update it. Because last removed character helps in maintaining the string such that there are no adjacent duplicates in the remaining string.
• Because, let's assume the last removed character is "b" and the first element of the remaining string is "b", then it means we will be having adjacent duplicates at the end of the result, so we need to remove these by using the last removed character using a while loop on a remaining string.

This can be clearly explained below:

this '$b$' has to be removed.

The recursive tree formed for removing adjacent duplicates is as follows:

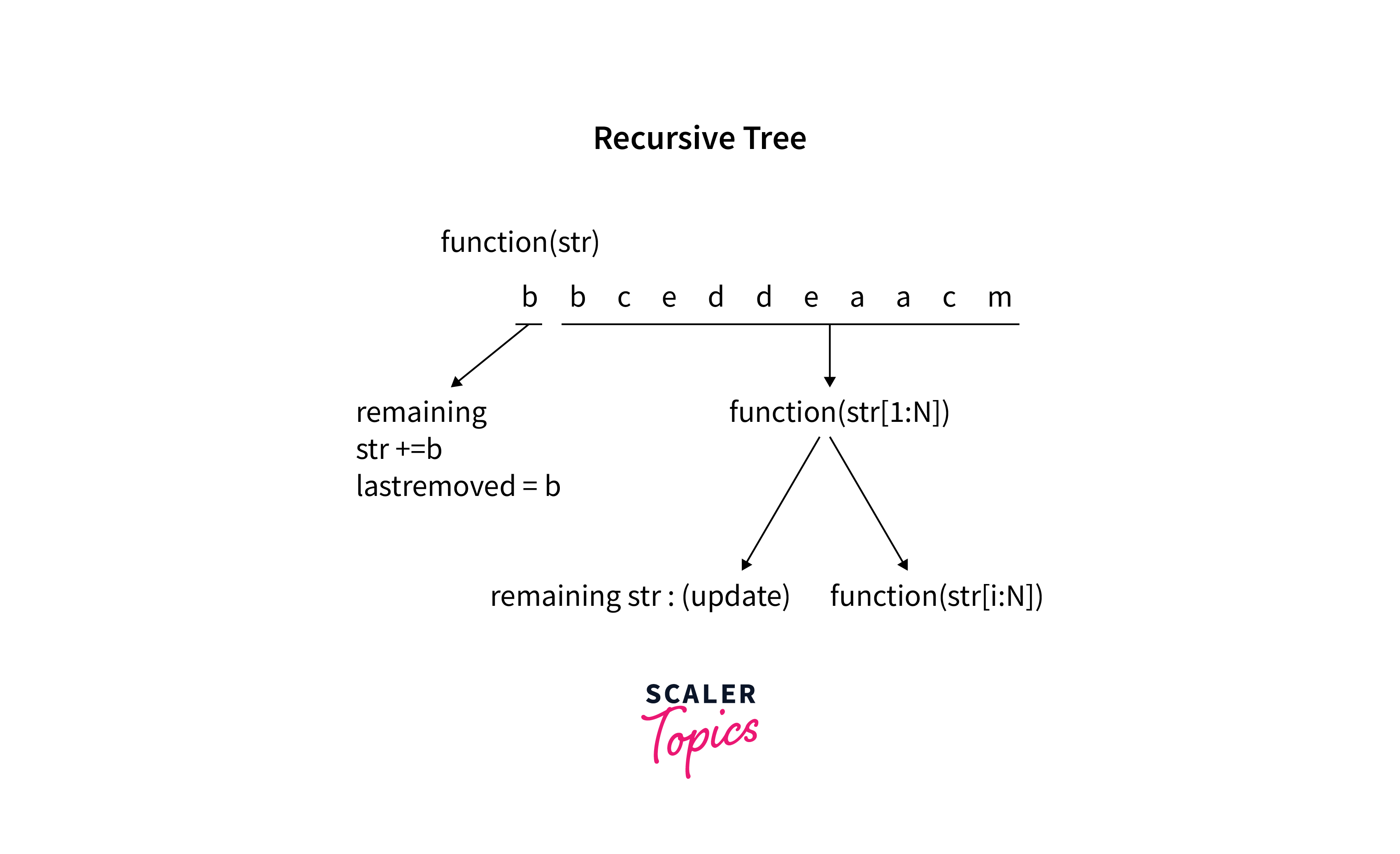
Implementation

Below is the implementation of the above approach for removing the adjacent duplicates using recursion by following the Schlemiel painter’s algorithm in C++, python, and java.

C++ implementation for removing adjacent duplicates using recursion:

Output:

m avcabvcb

Python implementation for removing adjacent duplicates using recursion:

Output:

m avcabvcb

Java implementation for removing adjacent duplicates using recursion:

Output:

m avcabvcb

Explanation:

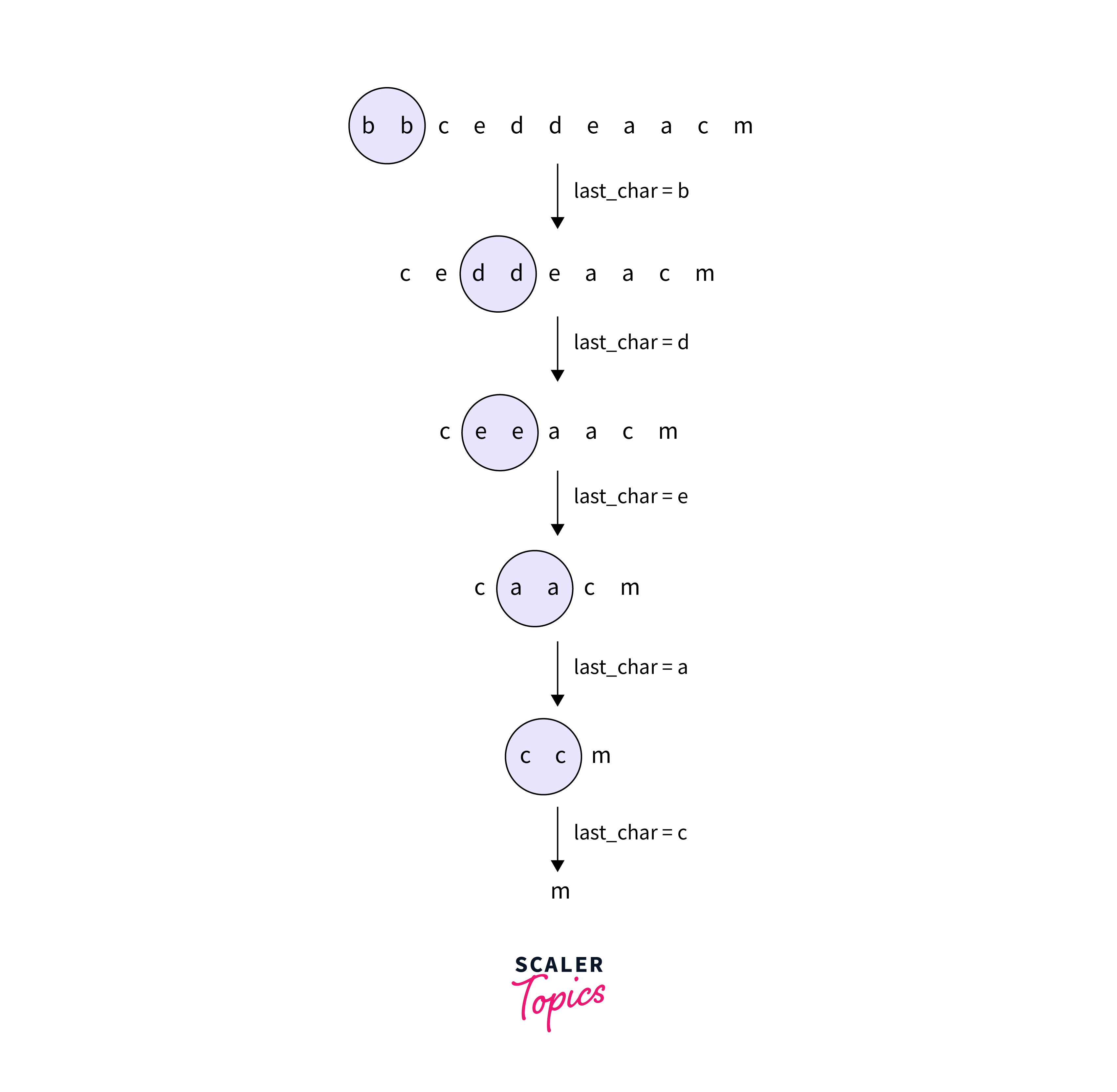
For the input string "bbceddeaacm", all the adjacent duplicates are removed using recursion. For a clear understanding of the approach, the below image clearly explains the approach by using the input string:

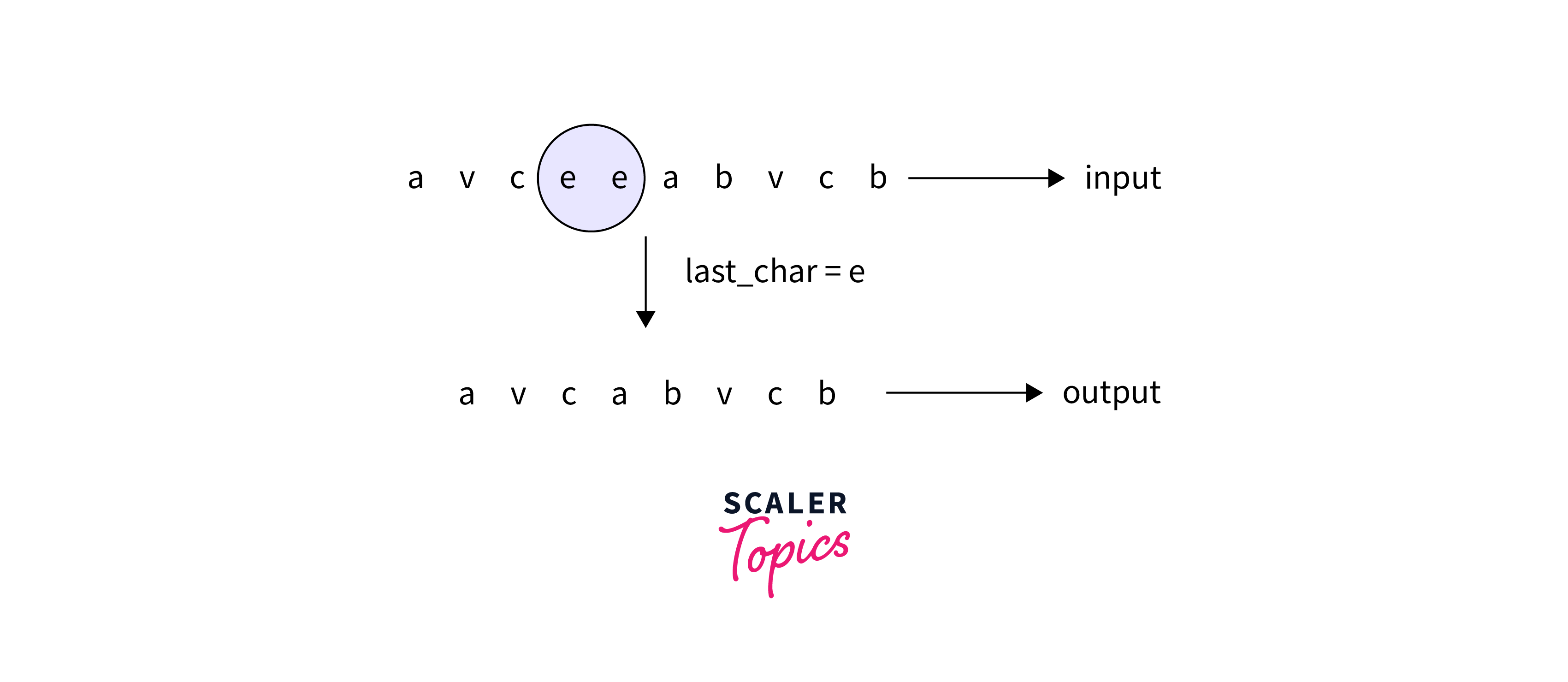
For the second input string "avceeabvcb" after removing all the adjacent duplicates using recursion, the remaining string obtained is "avcabvcb". The below image explains how recursion is implemented on the input string.

Complexity Analysis

Time Complexity: $O(N)$ where N is the length of the given input string.

• The recurrence relation obtained is $T(N) = T(N-K) + O(K)$, where K is the number of first characters which are the same in the original string and the remaining string. The value of K is obtained by counting the number of iterations where first characters are matching in original and remaining string.
• Because in each recurrence call we call for the recursive function for the remaining string and also remove the adjacent duplicates of size K, this has the time complexity of $O(K)$.
• By solving the recurrence relation the overall time complexity for removing adjacent duplicates using recursion is $O(N)$

Space Complexity: $O(N)$, where N is the length of the given input string.

• Extra space is needed for the auxiliary stack space used during the recursion.

Approach 2

Approach 2 is a slight modification of approach 1. In the above approach we have checked for characters matching at the starting of the index and removed it, similarly in this approach the basic idea is to check whether the remaining string's first character is matching with the last character of the original string (a string that is passed through the recursion). If the character is matched then we need to ignore that character before combining it with the remaining string in recursion, so it means that we are ignoring all the characters which makes the string with no duplicate characters. The remaining algorithm remains the same as the previous approach which is discussed above in the article.

Algorithm

Below is the algorithm to be followed for removing adjacent duplicates using recursion:

• Start traversing from the leftmost end of the given input string.
• Firstly we need to check whether the first character is matching with the second character in the string, if yes then we need to remove all duplicate characters using a while loop
• Every time we need to update the value of the last removed character and keep track of it using a variable, this is used to check for adjacent duplicates in every recursive call.
• After this call for the recursive function by passing the modified original string and updated last character.
• In the recursive call check whether the last character of the original string is matching with the starting character of the remaining string, if they are matching modify the value of the original and remaining string value by ignoring all the duplicate characters.
• At the end return the combination of the original string which has doesn't have duplicates and the remaining string(string in the recursive call which doesn't have any adjacent duplicates).

Implementation

Below is the implementation of the above approach for removing all adjacent duplicates using recursion:

C++ implementation for removing all adjacent duplicates using recursion:

Output:

nbcecm avckabvb

Python implementation for removing all adjacent duplicates using recursion:

Output:

nbcecm avckabvb

Java implementation for removing all adjacent duplicates using recursion:

Output:

nbcecm avckabvb

Explanation:

All the adjacent duplicates in the given input string are removed using recursion and return the output string. The output string doesn't have any adjacent duplicates. Recursion helps in removing all adjacent duplicates. For a clear understanding of this approach, the below image highlights the dry run.

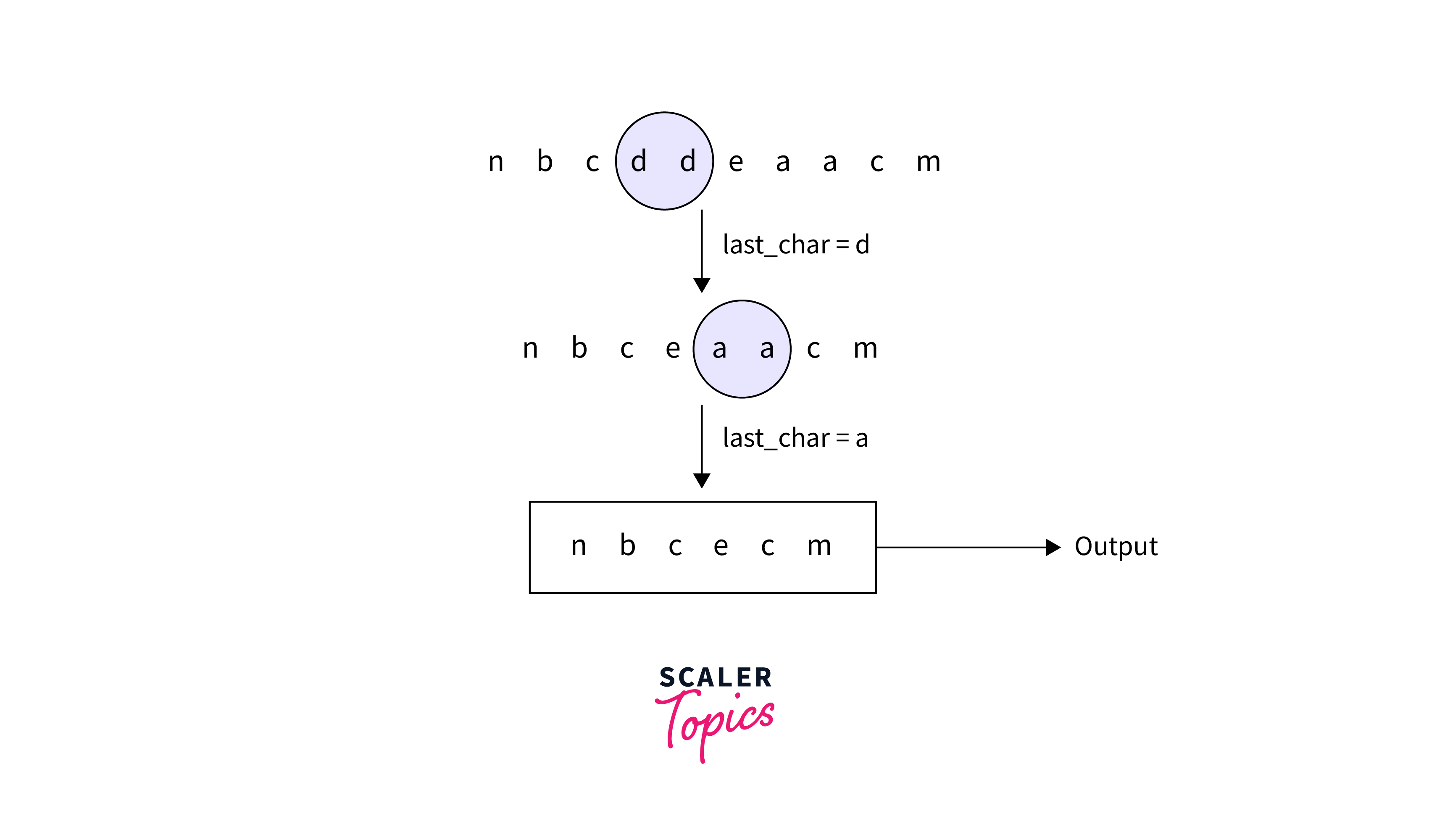
For the second input string, the dry run is as follows which is shown in the below image:

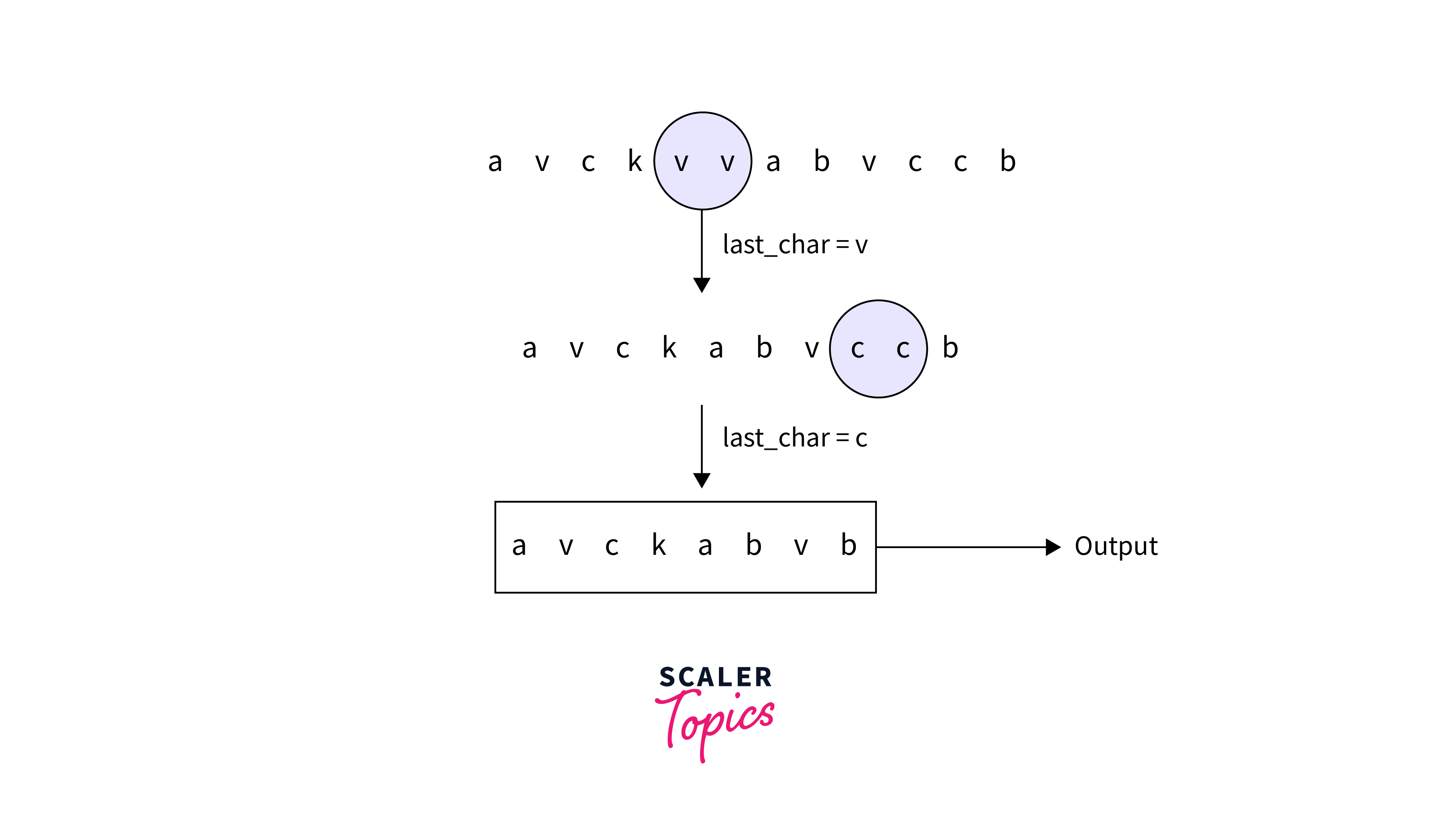
Complexity Analysis

Time Complexity: $O(N)$, where N is the length of the given input string.

• The recursive relation obtained is $T(N)= T(N-K-M) + O(K) +O(M)$, where K is the number of first characters that are the same in the original string and also in the remaining string. Whereas M is the number of matching characters in the remaining string and from the end of the original string. To remove all these matching characters we use a while loop, so it takes a time complexity of the length of characters that are matching.
• Removing all the matching characters in the original string and the remaining string takes a time complexity of $O(K)$.
• Removing all the matching characters from the start of the remaining string and the end of the original string is $O(M)$.
• By solving the recurrence relation, the overall time complexity obtained for removing all adjacent duplicates from the given input string is $O(N)$.

Space Complexity: $O(N)$, where N is the length of the given input string.

Extra space is needed during the recursion for auxiliary stack space.