Detect and Remove Loop in a Linked List

Problem Statement

We are given the head pointer of a linked list. Determine whether the linked list contains a loop or not. If it contains a loop, then we need to remove it as well from the given linked list.

There is a loop in a linked list if there is some node that can be reached again by continuously following the next pointer.

The loop must be removed from the linked list so that after the cycle is removed, the resulting linked list becomes linear and connected.

Example

Below is a linked list with a loop/cycle.

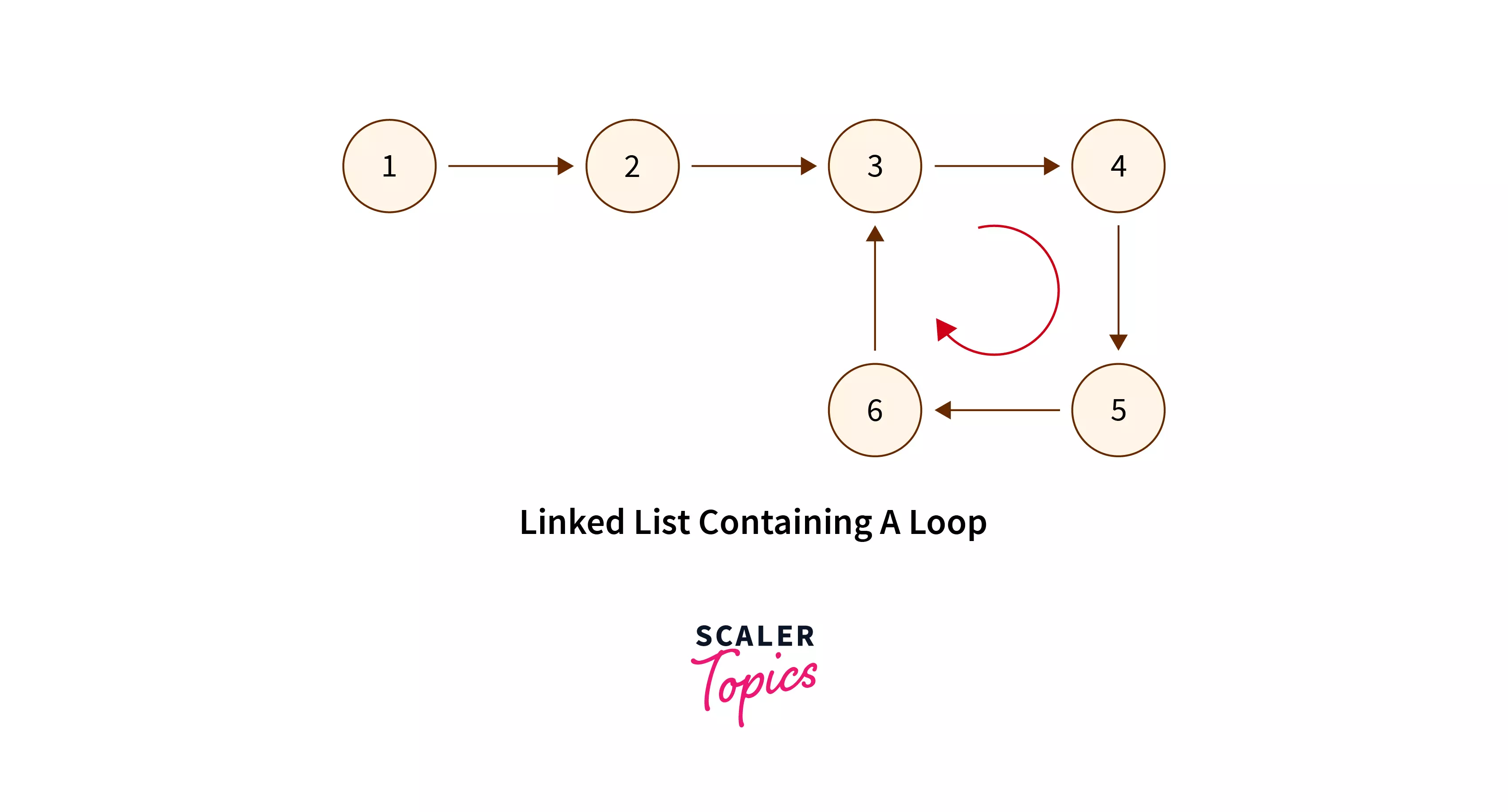
In the example mentioned above, if we start from the node 3, the path 3 -> 4 -> 5 -> 6 -> 3 forms a cycle. So, the linked list contains a cycle.

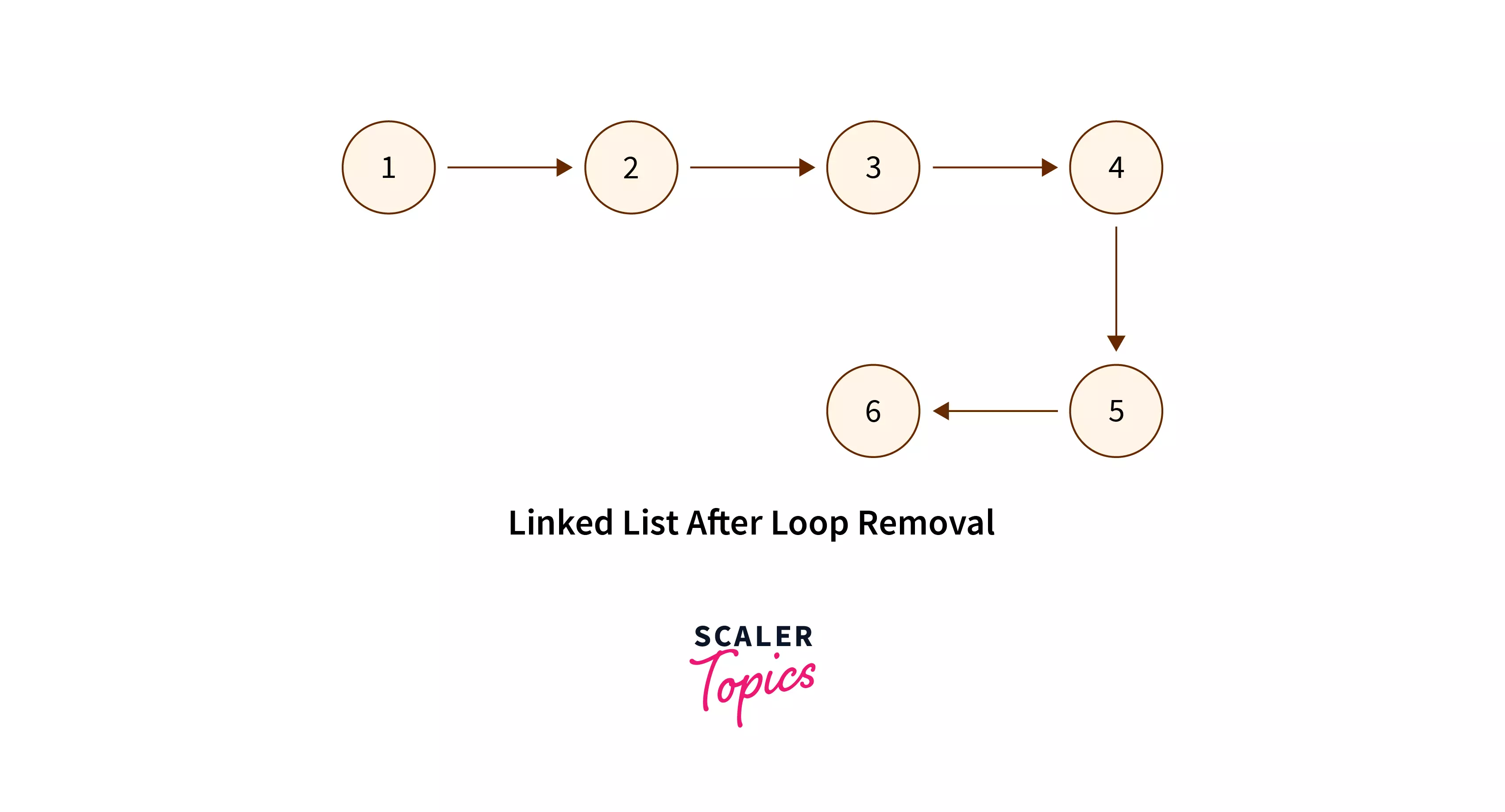
Below is the linked list after removing the link between the node with value 6 and the node with value 3.

Approach 1: Check One by One (code in Java, Python, C++)

In this approach, we first use Floyd's cycle detection algorithm, which is very efficient in detecting and removing loops in a linked list. Using Floyd's cycle detection algorithm allows us to detect and remove a loop from the linked list without using any extra space.

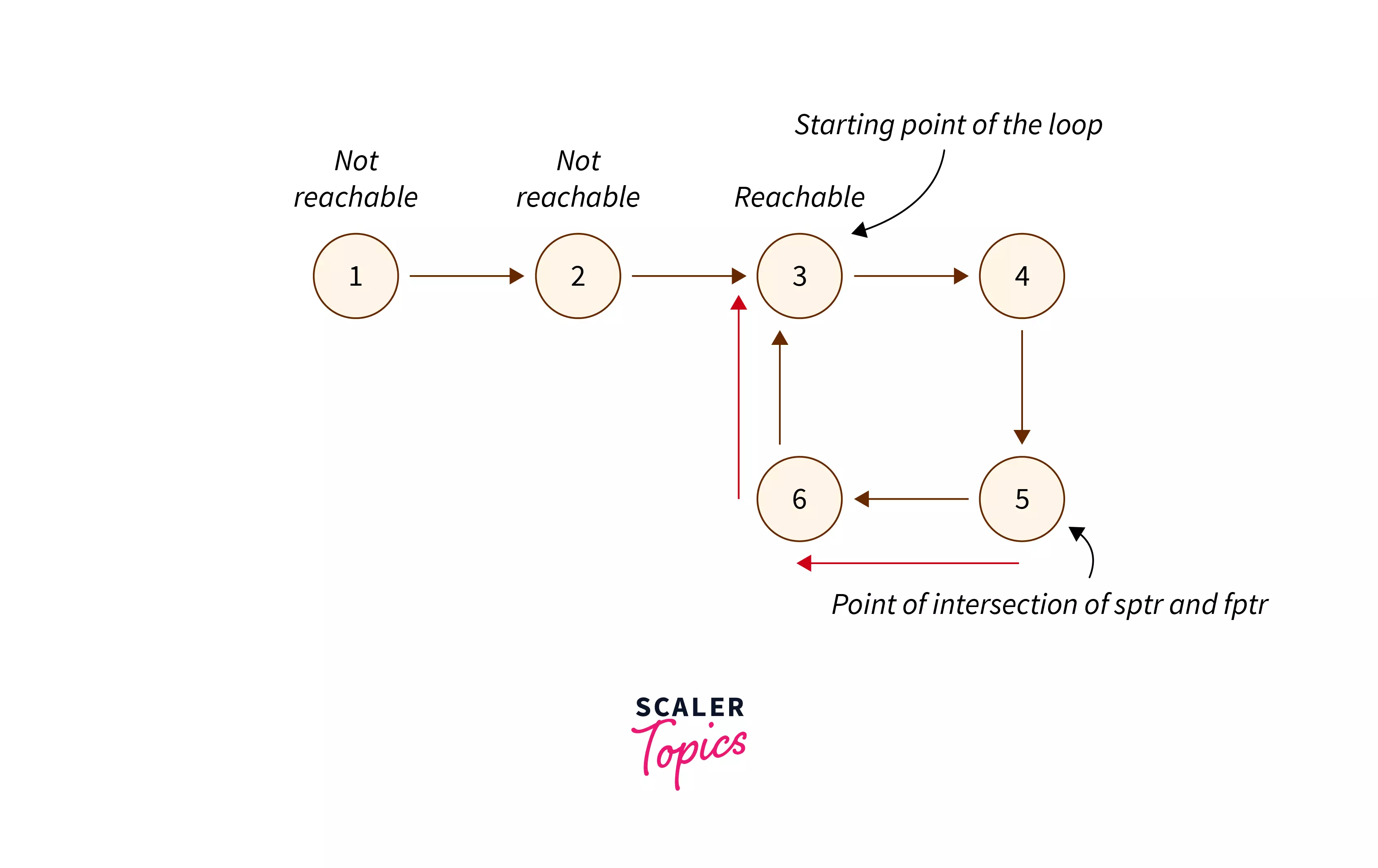
To find the starting point of the loop (so that we can delete the link between the starting and the ending node of the loop to remove the cycle), we can do the following.

Start from the head node of the linked list and check whether the node is reachable from the intersection point. If a node is reachable from the intersection point, this node is the starting point of the loop.

Code Implementation

Java

Python

C++

Complexity Analysis

The time and space complexity of the above approach is given below.

Time Complexity : Since for each node, we are checking whether it is reachable from the sptr node or not, the time complexity of the above approach is O(n^2).

Space Complexity : The space complexity for the above approach is O(1) since we are using only two pointers to detect the loop and no extra space.

Approach 2: Better Solution

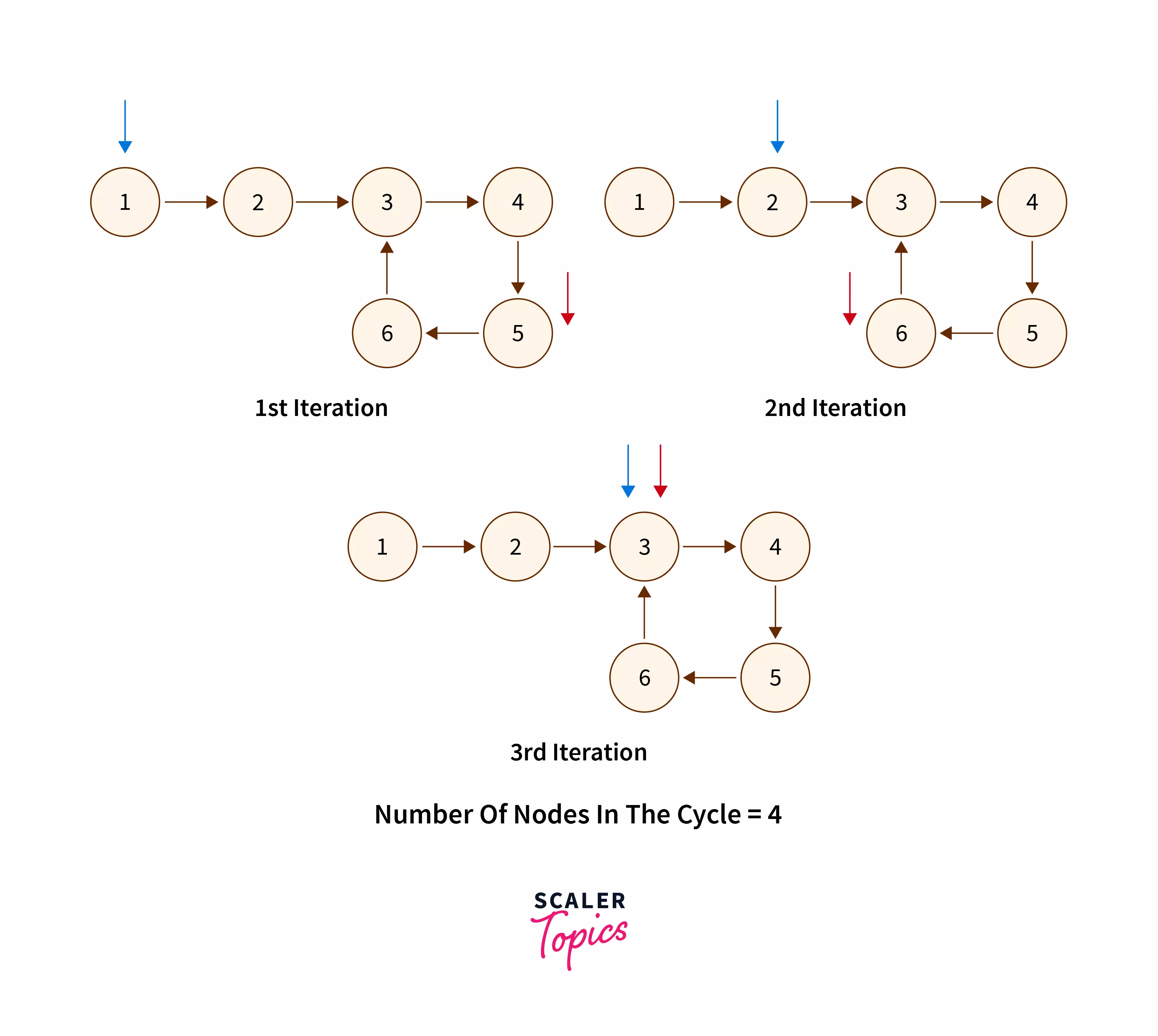
In this approach, we find the intersection point of the slow and fast pointers using Floyd's algorithm. Once intersected, count the nodes in the cycle starting from the slow pointer. Then, we will initiate two pointers: one from the head and another from a node 'ctr' distance away. Move them one node at a time until they meet; this intersection marks the start node of the loop.

This method efficiently identifies cycles in linked lists and determines their start points, ensuring optimal traversal for loop detection and node counting.

The graphical representation of how the two pointers will move in every iteration is given below.

Finally, we will remove the link between the start node and the preceding node to remove the cycle.

Code Implementation

Java

Python

C++

Complexity Analysis

Time Complexity : The time complexity of the above approach is O(n).

Space Complexity : The space complexity for the above approach is O(1) since we are using only two pointers to detect and remove the loop and no extra space.

Approach 3: Removing Loop Without Counting the Number of Nodes in the Cycle (code in Java, Python, C++)

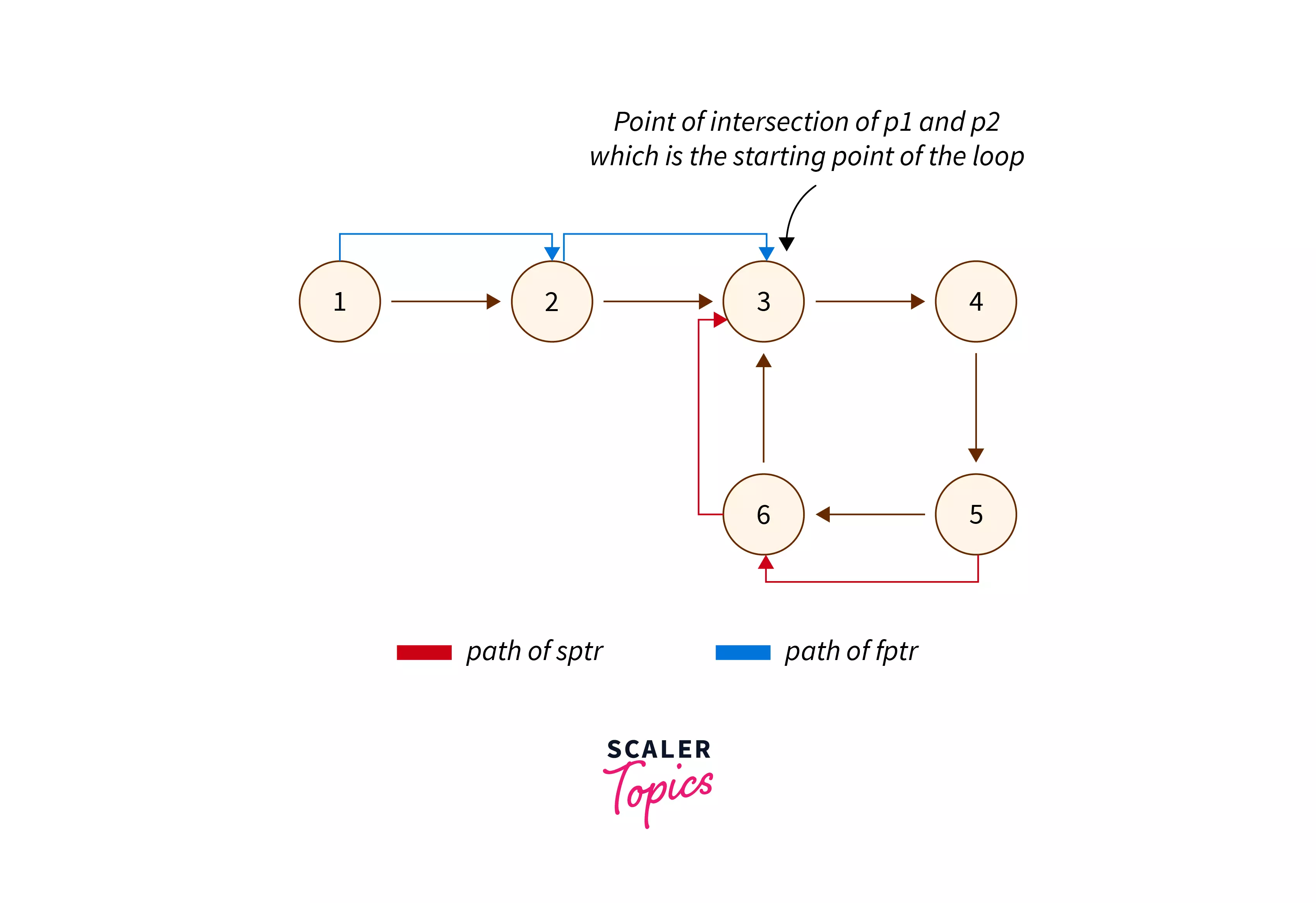
In this approach, after we know the loop exists in the linked list, we have to remove it. For this, we will take two pointers, p1 and p2. We initialize pointer p1 with the head of the linked list and pointer p2 with the point where the two pointers sptr and fptr become equal.

We will move the pointers p1 and p2 until we reach a state when p1->next becomes equal to p2->next. When the loop terminates, the pointer p2 will point at the node preceding the starting point of the node in the loop.

The representation of how the pointers p1 and p2 move until p1->next becomes equal to p2->next is given below.

To remove the cycle, we can just make p2->next = NULL. This will break the link between the p2 node and the starting point of the loop, removing the cycle.

Proof of Why This Approach Works

The above solution works because the loop's starting point is at the same distance from the head of the linked list and the point of intersection of sptr and fptr.

This can be proved by using fundamental physics concepts of speed, distance and time.

Given below is the path followed by sprt and fptr.

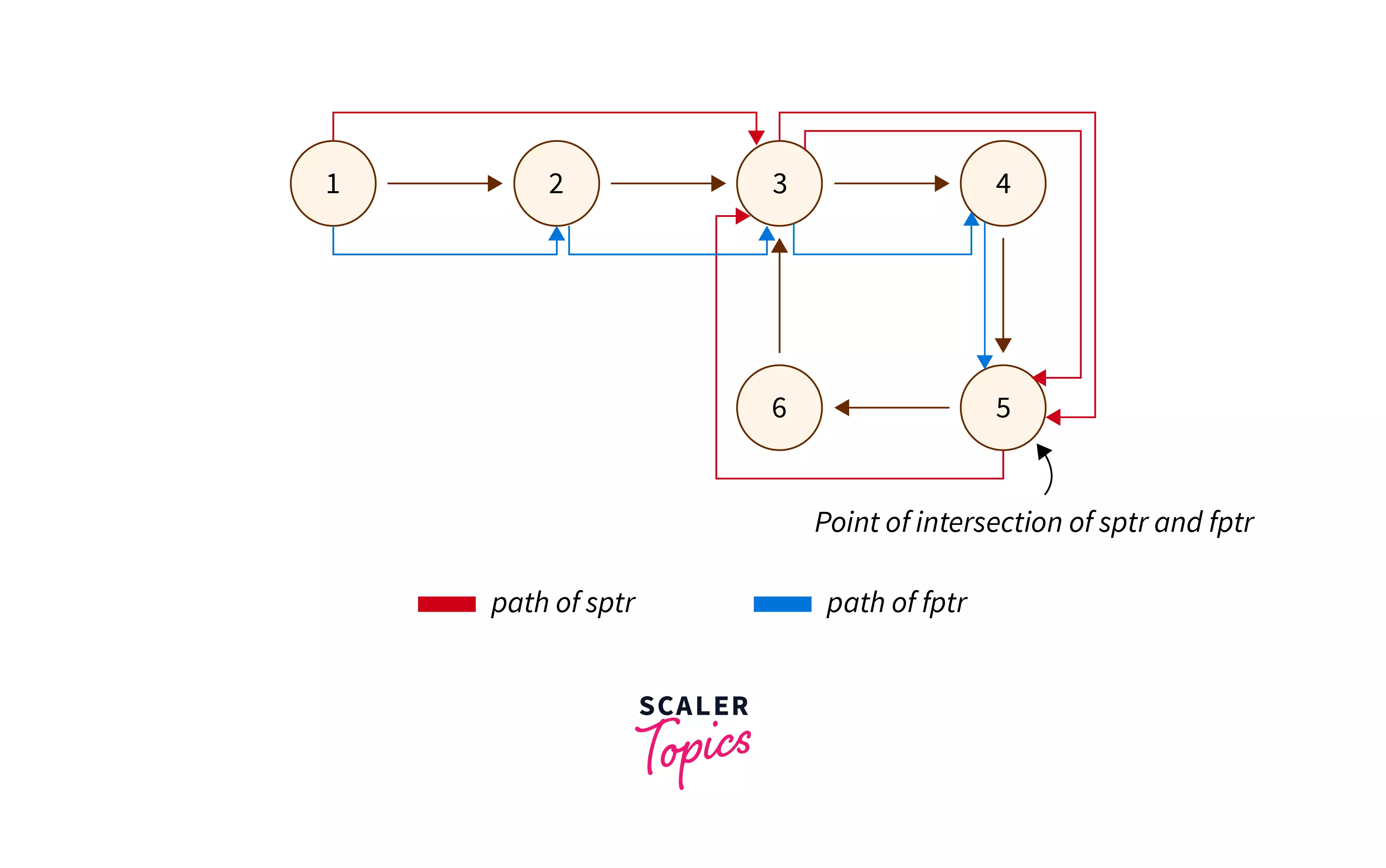
Let's define some distances. Let x be the distance between the head and the start node of the loop, y be the distance between the start node of the loop and the intersection point of sptr and fptr and z be the distance between the intersection point of sptr and fptr and the start node of the loop.

These distances are shown in the diagram given below.

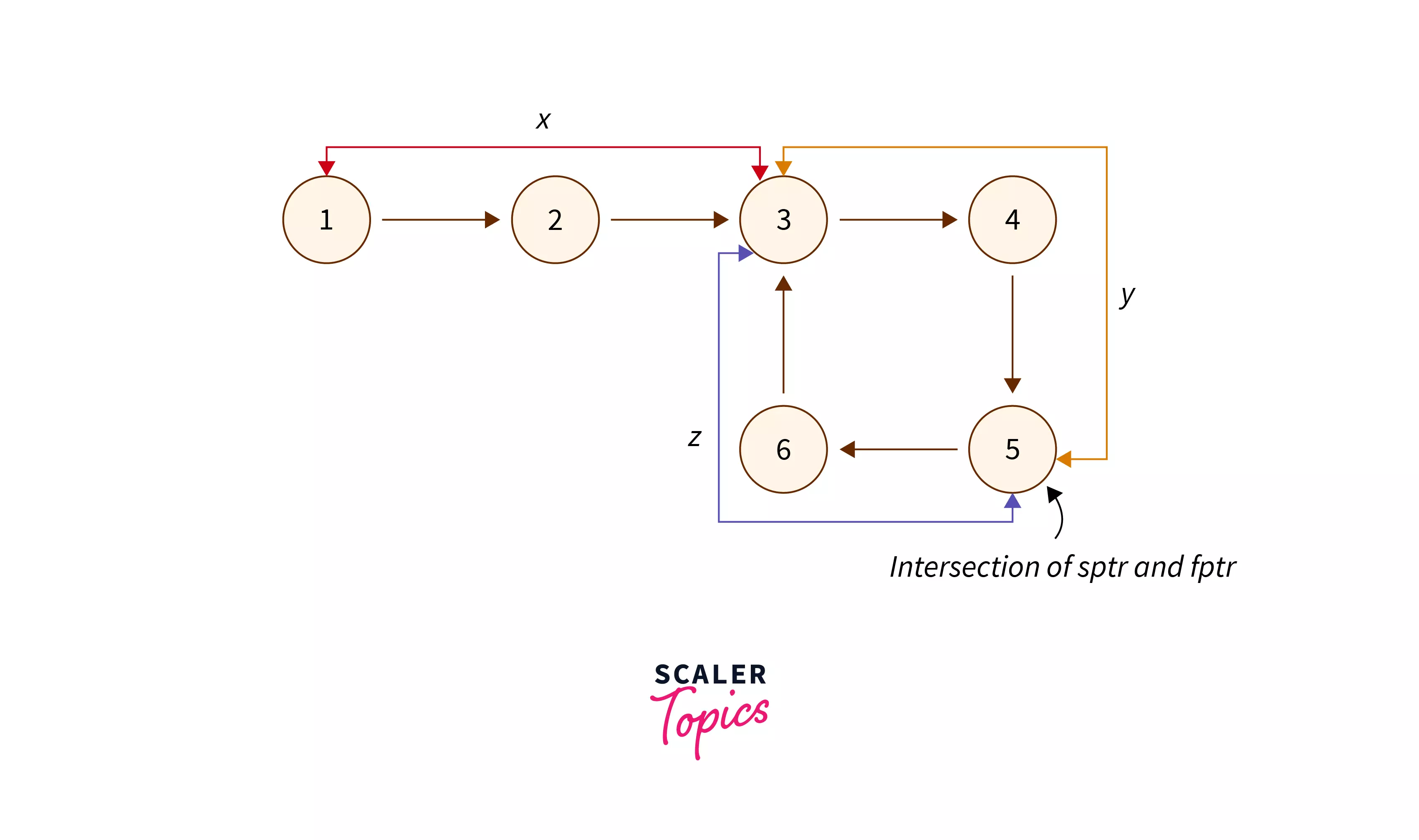
Looking at the above two images, we can say that the distance travelled by the pointer sptr = (x + y) and the distance travelled by the node fptr = (x + y + z + y) are equal to (x + 2y + z).

Since the speed of the fptr pointer is twice the speed of the sptr node, let the speeds of sptr and fptr be 'v' and '2v', respectively.

In physics, we have a formula - time = distance/speed. So, let's find the time the two pointers took to reach the intersection point.

Time taken by sptr to reach the intersection point => t1 = (x + y) / v ... (equation 1)

Time taken by fptr to reach the intersection point => t2 = (x + 2y + z) / 2v ... (equation 2)

Both sptr and fptr reach the intersection point at the same time, so from equations 1 and 2, we can deduce,

Finally, we have proved x (the distance between the head of the linked list and the starting point of the loop) is the same as z (the distance between the intersection point and the starting point of the loop).

Code Implementation

Java

Python

C++

Complexity Analysis

Time Complexity : Since we iterate over each node at most twice (twice in the case of nodes present in the loop), the time complexity of the above approach is O(n).

Space Complexity : The space complexity for the above approach is O(1) since we use only two pointers to detect and remove the loop and no extra space.

Approach 4: Hashing (Hash the Address of the Linked List Nodes)

This approach will use a hashmap to track which node has been visited while traversing the linked list. Below are the steps that explain the algorithms clearly.

1. We start from the head node and traverse the linked list.
2. If we arrive at a node already visited, this node is the first node of the cycle.
3. To remove the loop, we will arrive at a node just preceding the already visited node in the loop and remove the link between these two nodes.

Code Implementation

Java

Python

C++

Complexity Analysis

Time Complexity : Since we are traversing each node only one time, the time complexity of this approach will be O(n).

Space Complexity : Since we are using a hashmap to store the visited status of each node, the space complexity of the above approach is O(n).