Rotate Array (Java,C++,Python)

"Rotate array" refers to the process of rearranging the elements within an array by shifting each element to a new position. This rearrangement can be performed either clockwise or counterclockwise.

Types of Array Rotation in Array

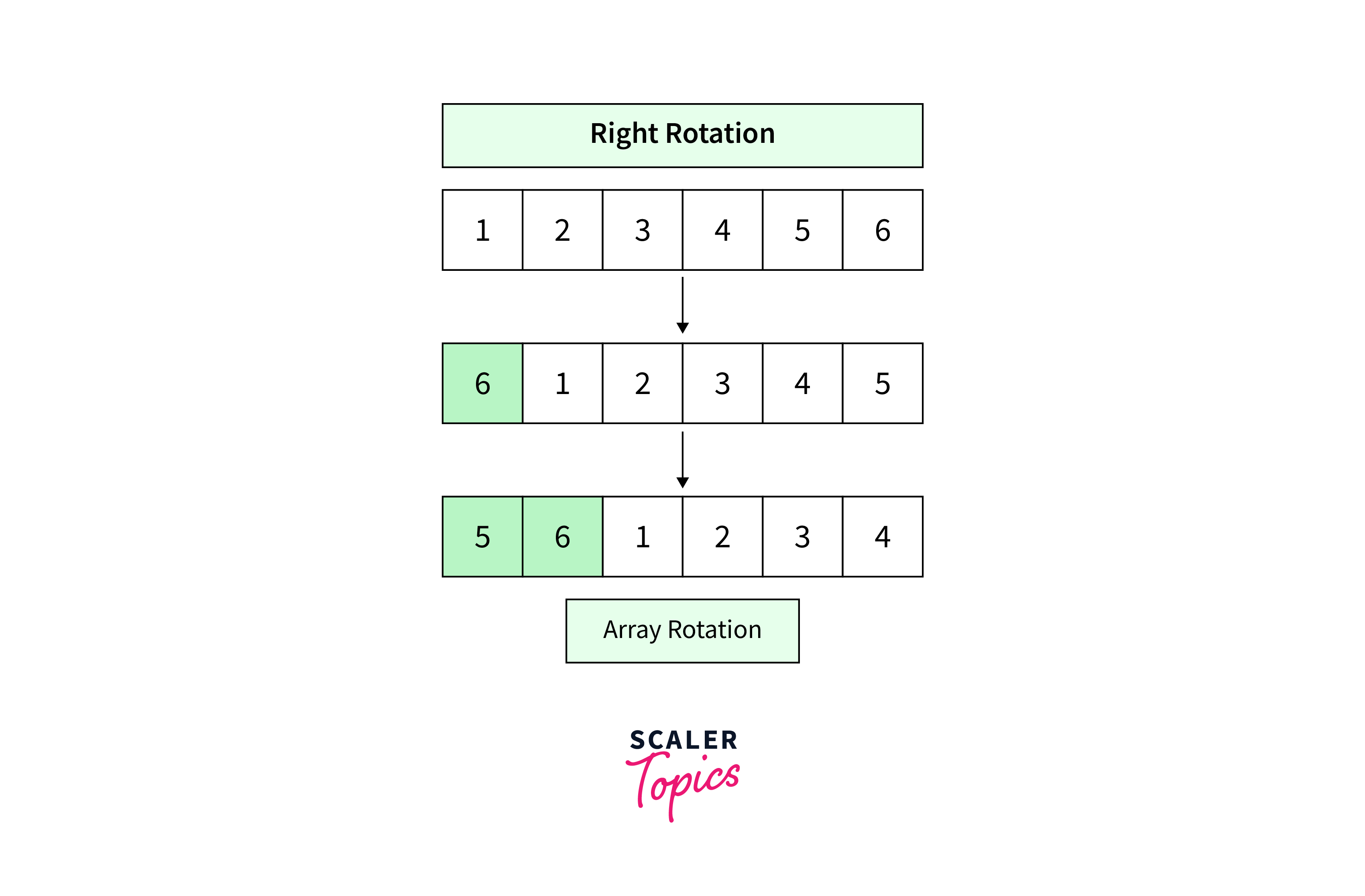
Right Rotation

In right rotation, the array elements are shifted towards the right. Each element moves to the position one step to the right, and the last element moves to the first position.

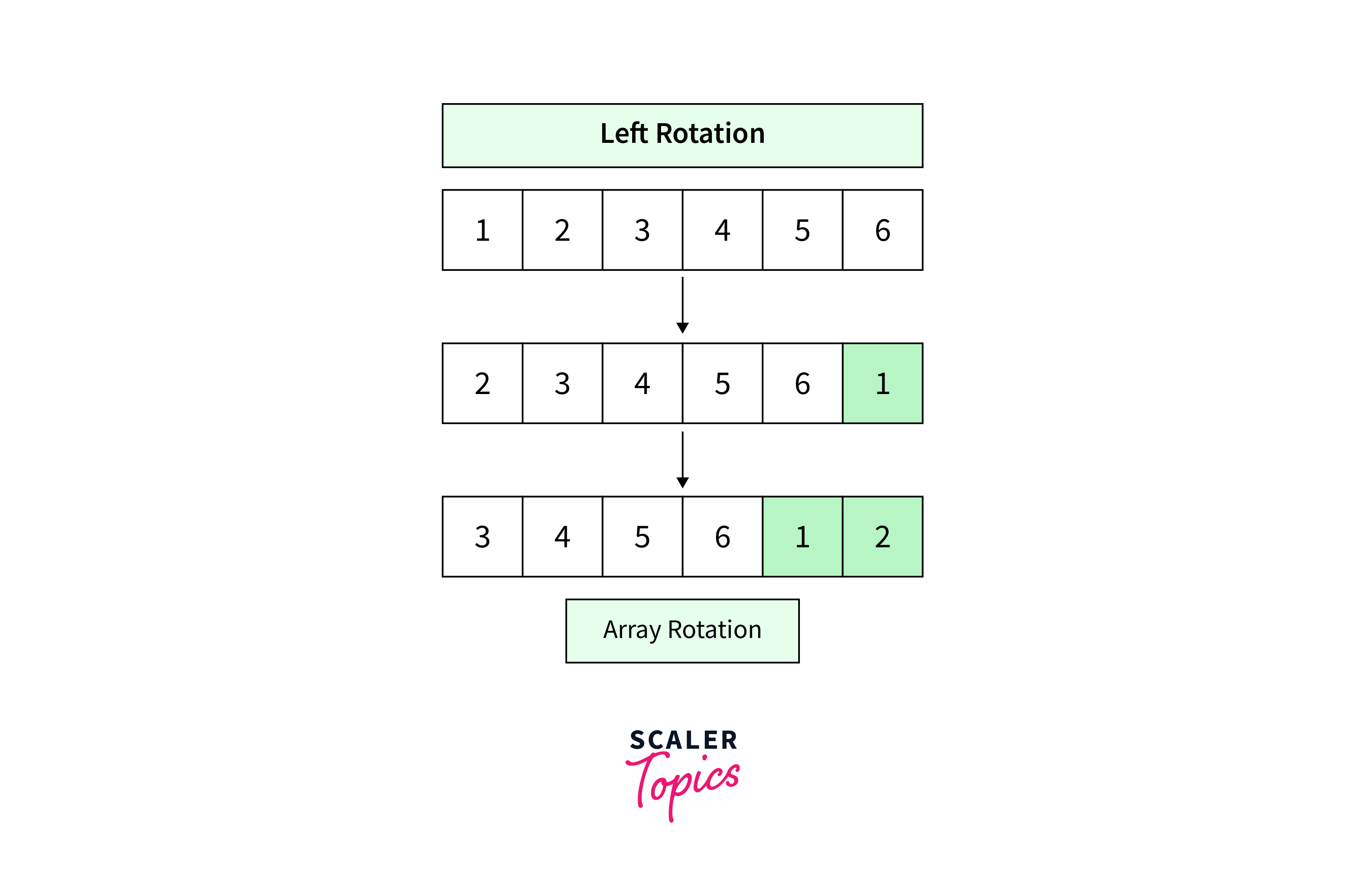
Left Rotation

In left rotation, the array elements are shifted towards the left. Each element moves to the position one step to the left, and the first element moves to the last position.

How to Implement Rotations in an Array?

1. Rotate One by One

• In this method array is rotated one by one k times.
• While rotating always store the first element in a temp array and shift rest of the elements by one step.
• Example - arr =[1,2,3,4,5,6] , k=2
  • rotate array by one step (left rotation) - arr = [2,3,4,5,6,1]
  • rotate array again by one step (left rotation) - arr=[3,4,5,6,1,2]

C++ Implementation (Rotate Array - C++)

Java Implementation (Rotate Array - Java)

Python Implementation (Rotate Array - Python)

Complexity Analysis

• Time Complexity - O(n*k)
• Space Complexity - O(1)

2. Using Temporary Array

• arr = [10,20,30,40,50,60], k=2
• Store first k elements in a temp array. temp =[10,20]
• Shift rest of the array elements left by k steps. arr = [30,40,50,60,50,60]
• Restore the temp array elements in the original arr in last k positions. arr = [30,40,50,60,10,20]

C++ Implementation (Rotate Array - C++)

Java Implementation (Rotate Array - Java)

Python Implementation (Rotate Array - python)

Complexity Analysis

• Time Complexity - O(n)
• Space Complexity - O(n)

3. Juggling Algorithm

• This method is an extension of the Rotate array one by one method.
• In juggling algorithm, the given array is divided into different sets where number of sets is equal to GCD(n, k), where n is the length of array.
• The elements are then moved k positions to the left within the sets.
• Let's take an example and see how juggling algorithm works - arr = [1,2,3,4,5,6,7,8,9,10,11,12] and k=3
• In the above example the length of the array n=12 and k=3. The GCD of 12 and 3 is 3.
• So, the array will be divided into 3 sets and the elements will be moved among the sets.
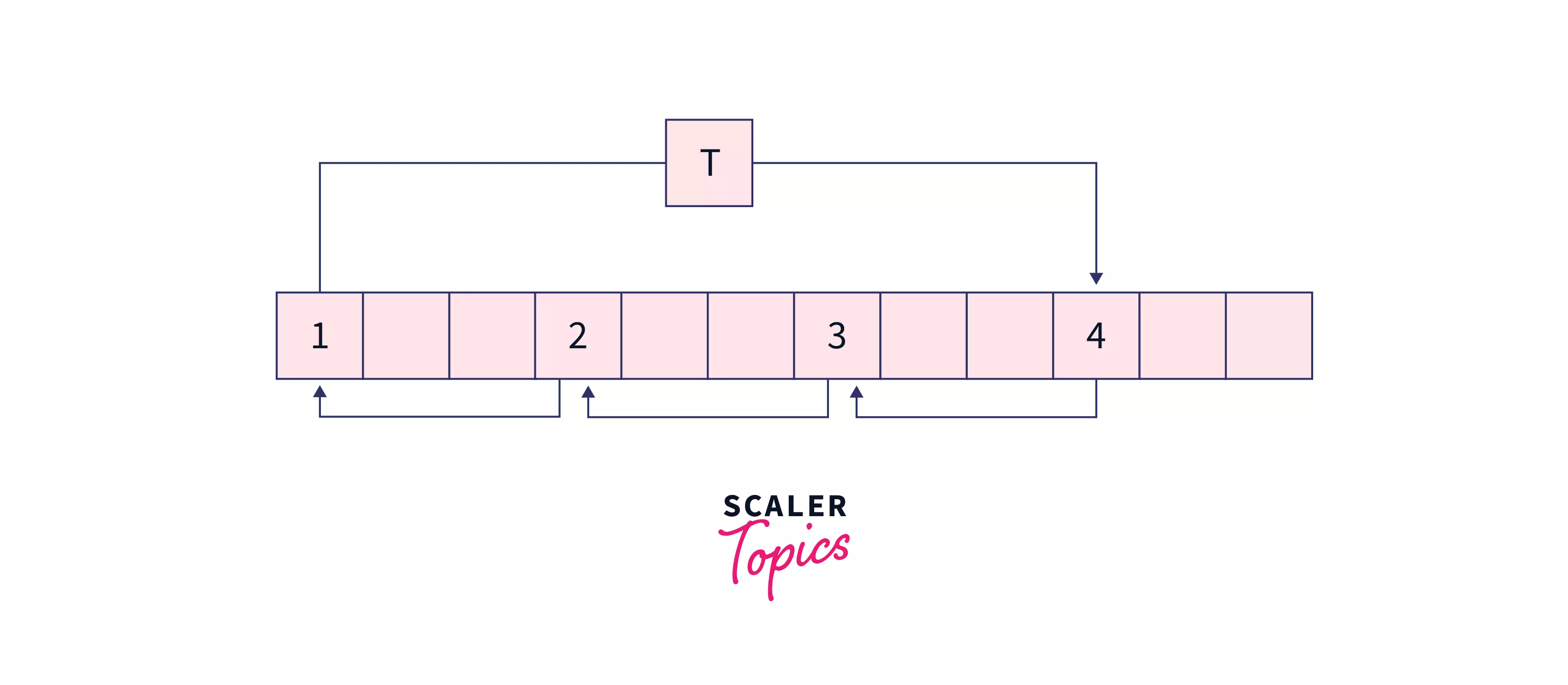
• After first step, elements are moved in first set as shown in the figure above. The array after first step will be [4 2 3 7 5 6 10 8 9 1 11 12]
• Similarly, After second set move - arr= [4 5 3 7 8 6 10 11 9 1 2 12]
• After third set move - arr= [4 5 6 7 8 9 10 11 12 1 2 3]

C++ Implementation (Rotate Array - C++)

Java Implementation (Rotate Array - Java)

Python Implementation (Rotate Array - Python)

Complexity Analysis

• Time Complexity - O(n)
• Space Complexity - O(1)

4. The Reversal Algorithm

• By observing the pattern in the rotation of the array, it can be thought of to be made of two parts arr[0..K-1] and arr[k..n-1], where n= size of array.
• Reverse the arr[0...k-1]
• Reverse the arr[k...n-1]
• Reverse the whole array [0...n-1]
• Lets's take an example - arr = [1,2,3,4,5,6,7],k=3, length of the arr(n) =7
• After reversing arr[0..k-1] we get - [3,2,1,4,5,6,7]
• After reversing arr[k..n-1] we get - [3,2,1,7,6,5,4]
• After reversing the whole arr[0...n-1] we get [4,5,6,7,1,2,3]

C++ Implementation (Rotate Array - C++)

Java Implementation (Rotate Array - Java)

Python Implementation (Rotate Array - Python)

Complexity Analysis

• Time Complexity - O(n)
• Space Complexity - O(1)

Applications of Array Rotation

1. Search in a Sorted and Rotated Array: Efficiently searching in a sorted and rotated array can be achieved using algorithms like binary search, which capitalize on the rotation to find elements quickly.
2. Image Processing and Computer Vision: In image processing and computer vision applications, array rotations play a crucial role in tasks such as image transformation, alignment, registration, and feature detection, enabling various image manipulation and analysis techniques.
3. Text Editing and Processing: Text editing software utilizes array rotations for implementing text selection, deletion operations, as well as undo and redo functionalities, allowing users to manipulate and navigate through text efficiently.
4. Audio and Video Processing: Array rotation techniques are employed for applying effects like pitch shifting, time stretching, stereo panning, and creating dynamic visual effects.

Advantages of Rotations in an Array

1. Array rotation can optimize performance by enabling the use of more efficient algorithms or data structures for operations like searches or lookups. This optimization can lead to faster processing times and improved overall efficiency.
2. Array rotation simplifies computations, particularly in scenarios involving matrices. For example, rotating a matrix can streamline operations such as matrix-vector multiplication by facilitating the use of simpler computation methods like the dot product, thereby reducing complexity and enhancing computational efficiency.
3. By rotating an array, you can transform its representation, making it more adaptable and easier to work with or analyze. For instance, rotating a matrix can facilitate its representation as a vector or alter the orientation of the data, enhancing flexibility in data manipulation.