Square Root in C++

What is Meant by the Square Root of a Number?

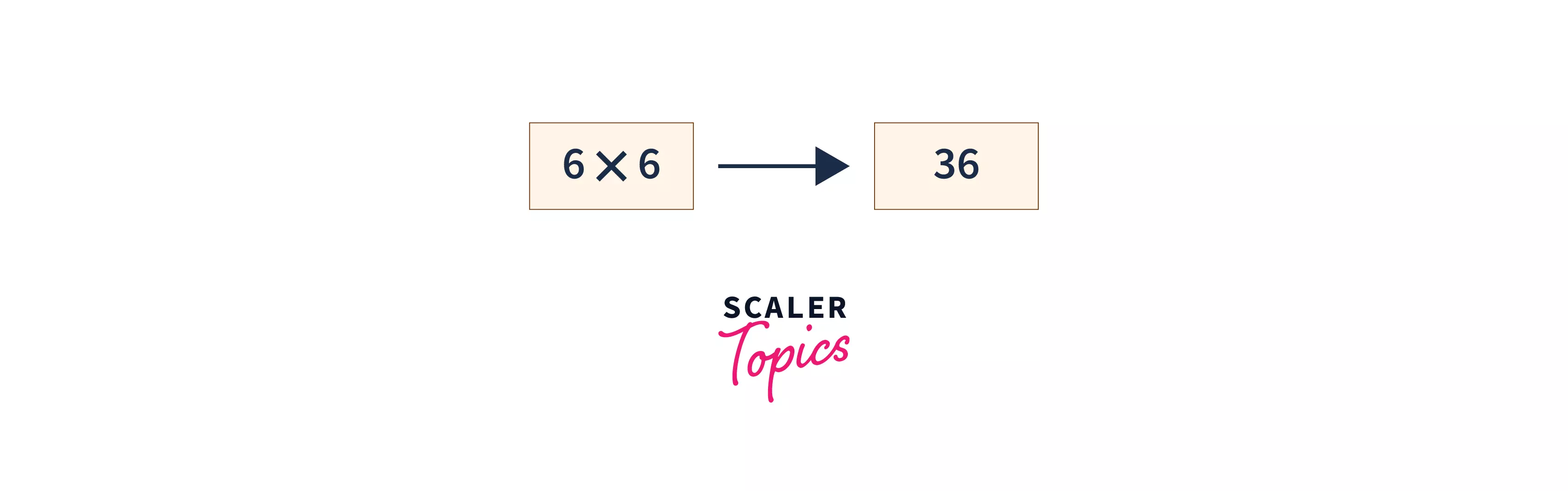
The square root of a number n is a number that, when multiplied by itself, results in n.

Hence if $s^2 = n$ then s is the square root of n.

Example: $6^2 = 36$, which means that 6 is the square root of 36.

Introduction to Square Root in C++

In C++, we will see two ways to find square roots broadly. One way is to develop our own algorithm, and the other uses in-built libraries. To develop an algorithmic approach, we need to understand that there is no straightforward mathematical formula to calculate the square root of a number. Hence we need to think of something innovative.

Instead of asking the question "what is the square root of a number", we shall ask " which number's square is the number we have been given". Thus, given a number n, we shall try to find the number s such that $s^2 = n$.

Brute Force Approach to Finding the Square Root

Let us use the brute force approach to find the square root of a number.

Assume the number for which we have to find the square root is n. We know that the square root of n would be less than n or greater than 0. Let us say we must find the square root to precision 3 (we can never calculate the square root of any non-perfect square with complete precision).

1. We will start with s = 0.001
2. Multiply the number with itself and check if the obtained number is greater than n.
3. If not, increase s by 0.001 and go to step 2.
4. If s is greater than n, return the value of s as the answer.

Time complexity

The two operations we are doing in the above code are:

Assuming the cost of both operations is 1, we can compute the total time complexity. The first operation occurs p times, so the time complexity is O( p ). We need to understand how the for loop runs for the second operation.

Let us take p as 3, so inc is 0.001. i starts at 0.001 and assumes values 0.002, 0.003, ... 1.000, 1.001, ... 2.000 and so on. Hence between two whole numbers, the loop runs $10^p$ times, and it runs till we have i = √ n

Hence total number of times loop runs till we reach i = √ n is i = $10^p$ * √ n

Thus the total time complexity is O( p ) + O($10^p$ * √ n) ≈ O($10^p$ * √ n).

Finding Square Root Using Binary Search

Let us see if we can do better than the above solution. Since we are "searching" for the number whose square is equal to the given number, what if we apply binary search to limit our iterations?

Let us simplify the problem by assuming that we only have to find the square root of perfect squares (a perfect square is a number whose square root is a natural number).

Our search window to start with shall be [1,n]. We shall keep halving the search window every iteration by updating the lower or upper bound of the window. If the square of the middle of our search window is greater than n, we know that the square root of n lies in the lower half of our window. Similarly, if the square of the middle of our search window is lesser than n, we know that the square root of n lies in the greater half of our window.

1. We will set the lower bound of our search to 1 and the higher bound to n.
2. We will set a mid-value as (lower_bound + upper_bound)/2.
3. If the square of mid is greater than n, we will set the upper bound to just less than mid, i.e., mid - 1.
4. We will set the lower bound to just greater than `mid + 1.
5. If the square of mid is equal to n, we break.

Dry run

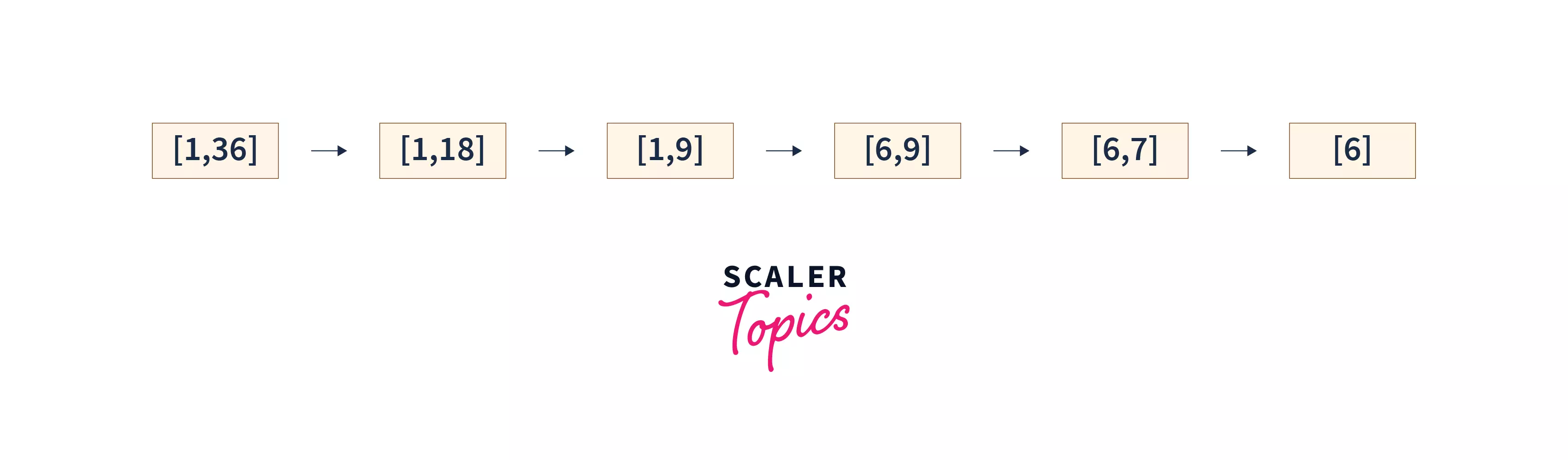
Let us take n = 36.

Iteration 1: Our search window is [1,36].

$mid = (1+36)/2 = 18$ $18^2 = 324$, which is greater than 36. Hence square root is present in the lower half of our window. We will update the upper bound to mid.

Iteration 2: New search window is [1,18].

$mid = (1+18)/2 = 9$ (integral division) $9^2 = 81$, which is greater than 36. Hence square root is present again in the lower half of our new window. We will update the upper bound to mid.

Iteration 3: The new search window is [1,9].

$mid = (1+9)/2 = 5$ $5^2 = 25$, which is smaller than 36.

Hence square root is present in the greater half of our new window. We will update the lower bound to mid + 1.

Iteration 4: The new search window is [6,9].

$mid = (6+9)/2 = 7$ $7^2 = 49$, which is greater than 36. Hence square root is present in the lower half of our new window. We will update the upper bound to mid.

Iteration 5: The new search window is [6,7].

$mid = (6+7)/2 = 6$ $6^2 = 36$, which is equal to 36. We shall print 6 as the answer and break out of the loop.

Time complexity

The time complexity of the above approach is the number of times our while loop runs (assuming the cost of each iteration is 1). If our initial window is [1,n], the size of our search space is n, which is being halved every iteration (either the lower bound is doubled or the upper bound is halved). This keeps going until our search window cannot shrink further; that is when upper_bound = lower+bound + 1. Thus the window assumes the size of n, n/2, n/4... 2, which takes log(n) iterations. Hence the binary search algorithm (assuming perfect squares) to find the square root of a number has the time complexity O(log(n)).

Finding Square Root in C++ by Using Predefined Function

In C++, we can use the pow function of the math.h library to find the square root of a number. pow function expects the exponent as an argument. Just like for finding the square, we use 2 as the exponent; for square root, we need to use 1/2 as the exponent.

Alternatively, we can use the cmath library, which directly has an sqrt function.