Transpose of a Matrix in Python

Introduction to Matrix Transpose in Python

Before learning how to transpose a matrix in Python, we should first understand the matrix and transpose of a matrix.

A matrix is a rectangular array of some data(numbers, letters, or other objects) arranged in the form of rows and columns. A matrix is composed of rows and columns. If the number of rows is N and the number of columns is M. Then we say the matrix is a N x M matrix. Refer to the image below to see how a matrix is represented using subscripts.

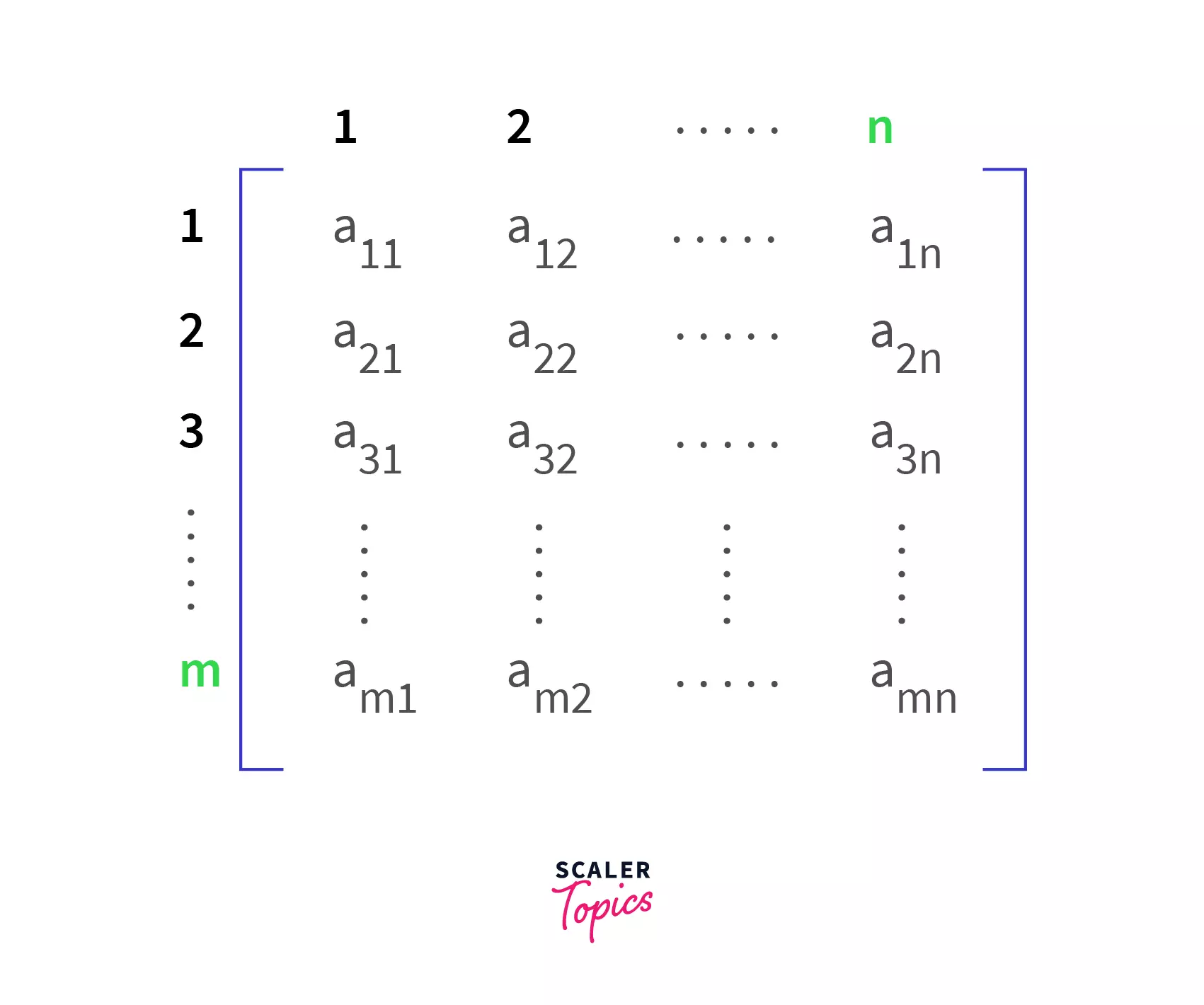
Now, the transpose of the matrix is nothing but a matrix obtained by changing the rows into columns and columns into rows. If a matrix is initially N x M (N is several rows and M is several columns), then after the transpose, the matrix becomes M x N (M is the number of rows and N is several columns). Refer to the image below to visualize the transpose of a matrix.

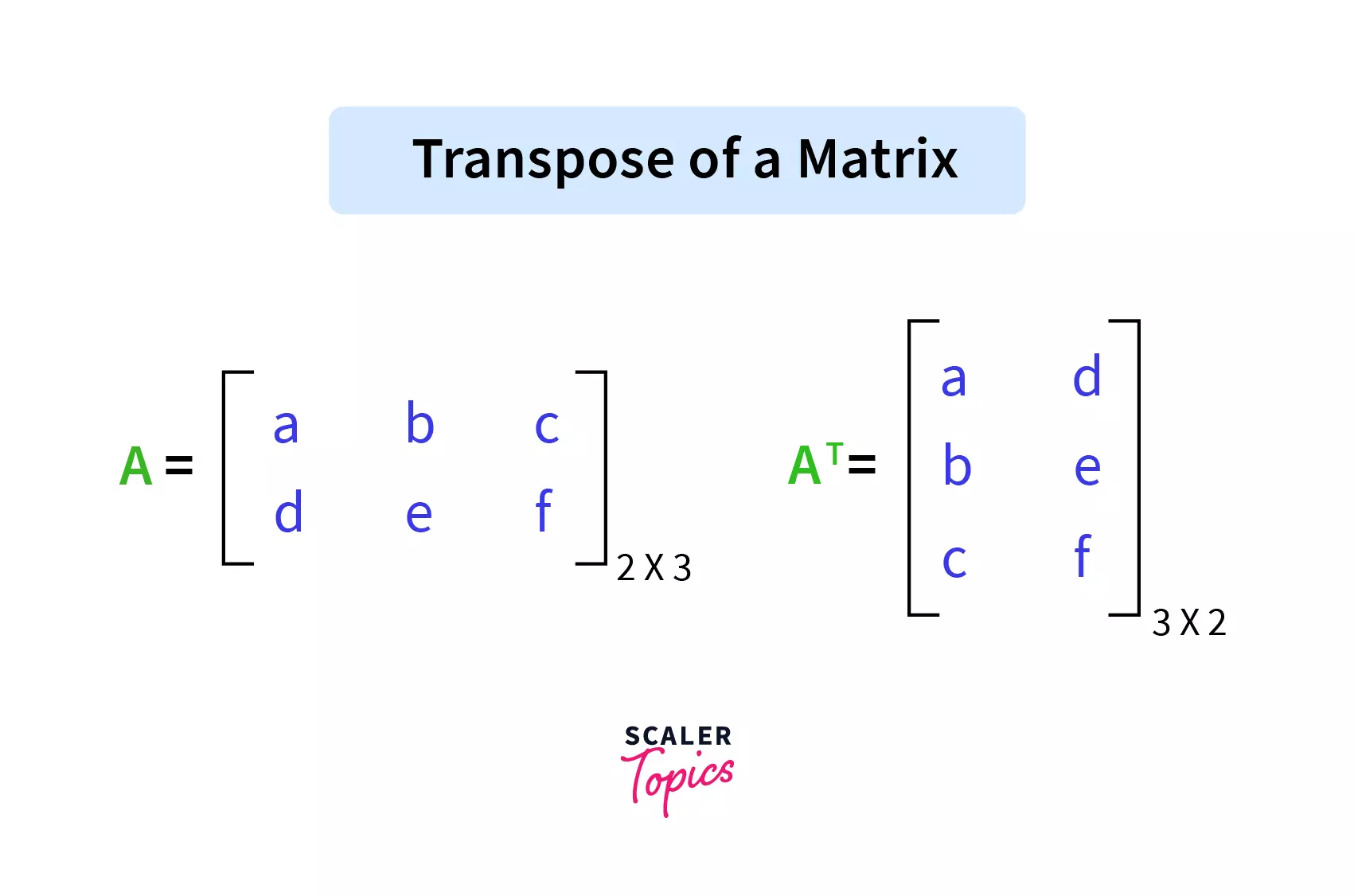
Note: Transpose of a matrix A is denoted by either A' or A^T.

Now, in python a matrix can be implemented using nested lists. Example: matrix = [[1, 2], [2, 3], [3, 4]] As we can see, the matrix has 3 rows and 2 columns so it is a 3x2 matrix. We can visualize the matrix as:

After the transpose, the matrix has 2 rows and 3 columns so it becomes a 2x3 matrix. The transpose of the matrix will look like as shown below:

The transpose of a matrix in Python can be implemented in various ways. Let us now discuss them one by one.

Transpose of a Matrix using Nested Loop

As we have seen, we can implement a matrix using nested lists(lists inside a list). So, we can use a nested loop (loop inside another loop). By running two loops (using I and j variables), we can change the value present at the ith row and jth column to the jth row and ith column. Refer to the code below for a better understanding.

Output:

Here, we are placing the matrix[i][j] element into the transpose[j][i].

Transpose of a Matrix using Nested List Comprehension

We have seen how to get transpose of a matrix in python using nested loops, but we can also use the pythonic way (shorter way). List comprehension (creating lists based on existing iterables) is very frequently used in these scenarios as list comprehension helps us to write concise codes (codes which take less space). Refer to the code below for a better understanding.

Output:

Transpose of a Matrix using Zip

We can also obtain the transpose of a matrix in python using the map() function and zip() function.

Let us see the code for better understanding.

Output:

Transpose of a Matrix using NumPy Library

So far, we have seen all the built-in methods of getting the transpose of a matrix in python. We can use a library named NumPy, built to work around arrays. The NumPy library helps us to work with large data sets and supports various methods that help us to work with multi-dimensional arrays efficiently. We will use the transpose() function of the NumPy library. Let us see the code for a better understanding.

Output:

For Square Matrix

The transpose of a square matrix results in another square matrix because the number of rows and columns are the same. Let us take an example of a square matrix (NxN):

Output:

For Rectangular Matrix

As we know, the transpose of an NxM matrix will result in an NxM matrix. Since N and M are of different values, the matrix is not considered a rectangular matrix. Let us take an example of the 2x5 matrix:

Output:

Learn More:

• What is PIP in Python?.