0-1 BFS

In normal BFS of a graph all edges have equal weight but in 0-1 BFS some edges may have 0 weight and some may have 1 weight.

For Example:

A vector, d will be defined to store distances between different vertices from source(s). d[s] will be 0 as the distance from source to source is 0. s will be pushed into the front of the deque(q). We’ll visit connected nodes and keep popping the previously pushed node at the front of the queue. We’ll assign u and w as first second edge respectively and push the edge connecting node having weight 0 to front of the queue and if the weight is 1, push it to the back of the queue, this will be repeated till the queue is empty which denotes all the nodes are visited.

Here is the basic code of the algorithm:

Let's understand this algorithm with a pictorial representation of a graph.

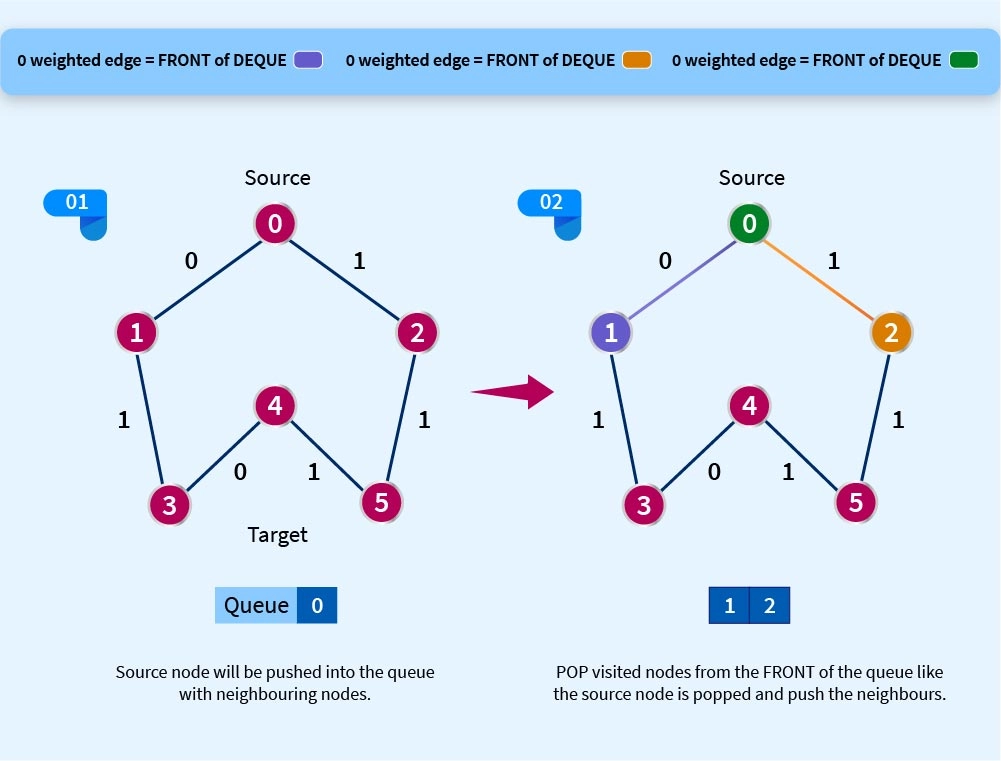
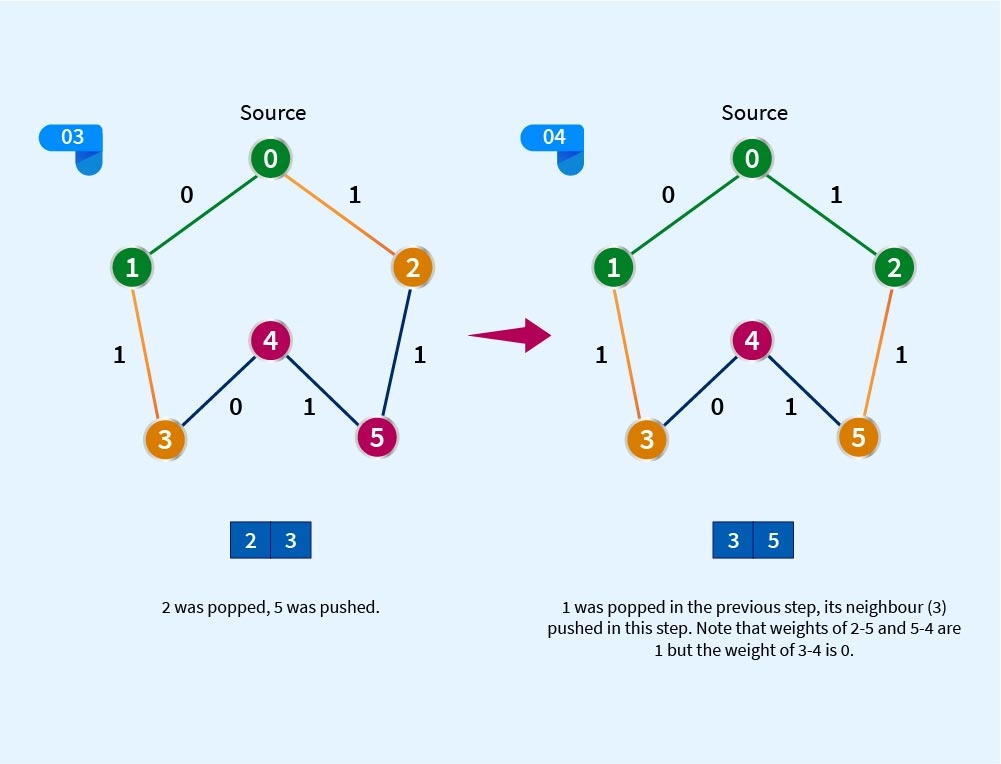
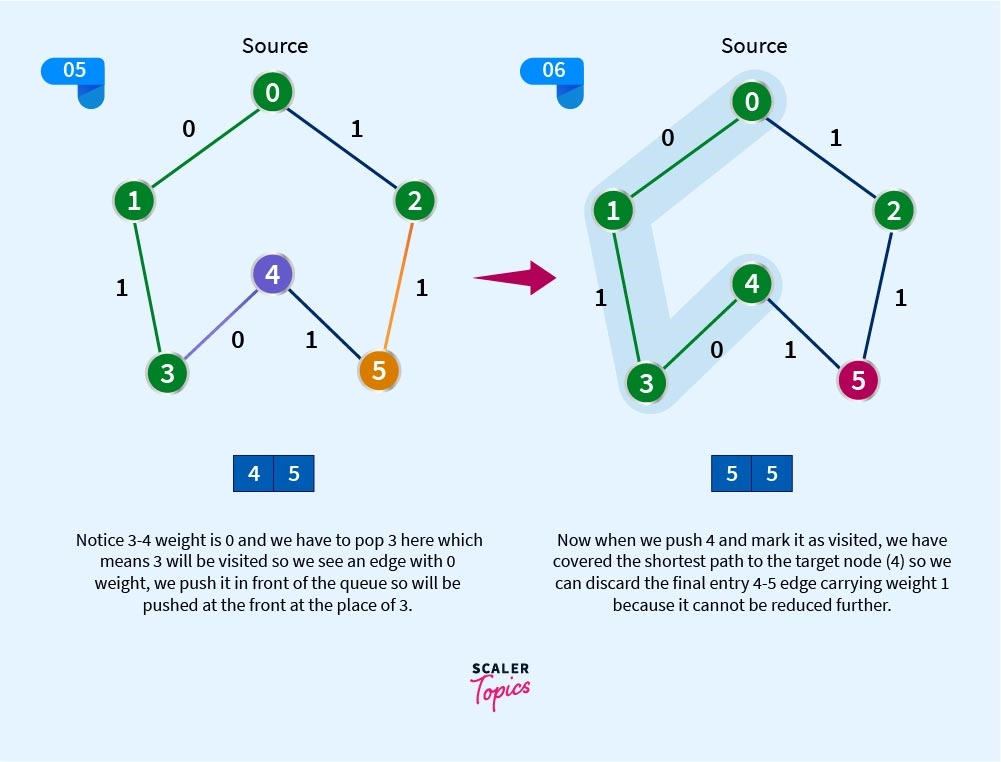
Explanation:

The edge with weight 1 will be pushed to the back of the queue so notice nodes 2,5,4 and 3 was added at the back of the queue as evident from the graph and the rest with weight 0 will be pushed in front, the front will always be popped (removed) after being pushed off course and the back element moves to the front, but when in the 5th step 3 was popped and due to 3-4 linkage have weight 0 therefore pushed in front.

Time Complexity:

Suppose a graph G, has V vertices and E edges. It is a weighted graph with boolean weights i.e. either 0 or 1.

So while traversing the graph, while visiting a vertex we know we only have two possibilities, an edge having weight 0 or another edge having weight 1, we also know the queue holds two consecutive successive elements (nodes).

So if the edge weight equals 0 we will push the node to the front and if not push it back to the end, this allows our queue to remain sorted.

Thus all the nodes are visited minimum once the concluding time taken to visit all nodes equals sum of the number of edges and vertices. So, the time complexity of 0-1 BFS is O(E + V), which is linear and more efficient than

Dijkstra: O(V2+E) -> (O(E + V Log V)

Example of 0-1 BFS Algorithm

Suppose a graph with V nodes and E edges. Edges have binary weights (0 or 1). The source node is the 2nd node and we need to find the shortest path from the source node to every other node. Seems sound na. Our logic remains the same, jog your memory with me…We will use a double-ended queue (DEQUE) because it allows insertion and deletion at both ends which is exactly what we need:

1. Traverse through all the nodes (first the source node will be pushed in front then its neighbour after popping source)
2. Checking the weight of all the edges
3. Pushing the nodes in the queue, if weight 0 then in front else back of the queue
4. Printing the sum of the weight of edges making shortest path from source node to other nodes

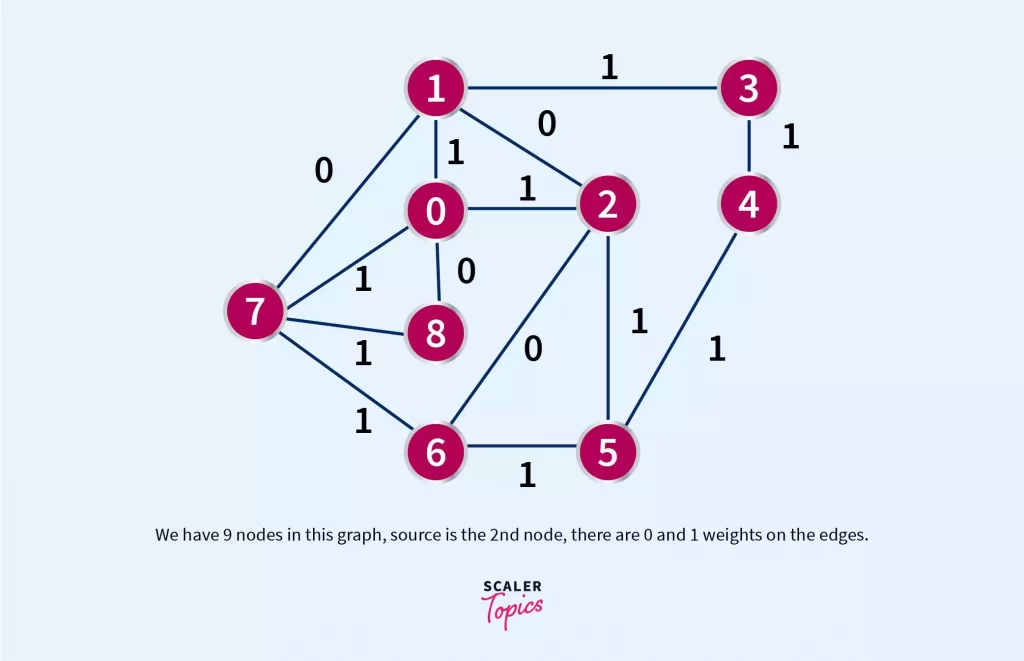
We have 9 nodes in this graph, source is the 2nd node, there are 0 and 1 weights on the edges.

Here is the code for the 0-1 BFS in C++. The above graph is taken as input to the program :

Output:

Practice this into a compiler and try manipulating the values if you understand the flow of code, make a graph yourself with pen paper and give edges 0 and 1 weight randomly, put the values in this code, run it, and match it.

Implementation of 0-1 BFS on Java and Python3

You can find the implementation of the above graph problem in Java and Python here:

Java Program

Python Program