Advanced Nim’s Game

Overview
The Nim Game is a combinatorial game that involves a number of piles of stones or coins and two players playing the game. In each turn, one player chooses a pile and removes a non-zero number of stones or coins from the pile. The person who cannot make a move loses in the end. We explore a variation of the standard Nim Game(Advance Nim Game or Zero Move Nim Game) and also define its solution.
Takeaways
Complexities of the nim's game
- Time Complexity :
- Space Complexity:
What is the Advance Game of Nim?
Let us discuss what the Standard Game of Nim or Nim Game is before we define the Advanced Game of Nim(Zero Move Nim Game).
The Game of Nim or Nim game is a mathematical combinatorial game in which we have a pile of some objects, say coins in this case, and two players who will take turns one after the other. In each turn, a player must pick at least one object(coin in this case), and may remove any number of objects(coins) given that they all belong to the same pile. The game is won by the one who picks the last object(coin).
In Advanced Game of Nim, for each non-empty pile, either of the players can remove zero items and be counted as its move, but this move can only be used once per pile by either of the players. This is a slight modification over the standard nim game.
Before we move on to the approach to solve the advanced game of nim, let us understand some terms related to the solution.
Grundy Number
A Grundy Number is a number that defines a state of a combinatorial game. Using Grundy Number we can define any Impartial Game(such as Nim Game).
Before we revisit the Grundy Number, let us understand another term MEX(Minimum Excludant).
MEX(Minimum Excludant)
Minimum Excludant (MEX)is the smallest non-negative number not present in a set of numbers, that is the minimum value of the complement set. The Minimum Excluded values are also used in greedy coloring algorithms in graph theory.
Lets take a look at some examples to understand how Minimum Excludant (or MEX) works:
Examples:
-
- The Minimum Excludant (or MEX) of a null set () is .
-
- The Minimum Excludant (or MEX) of this set is
-
- The Minimum Excludant (or MEX) of a set of all even numbers is the first odd number, that is .
-
- The Minimum Excludant (or MEX) of this set is .
-
- The Minimum Excludant (or MEX) of this set is , where is the ordinal limit of the natural numbers.
-
- The Minimum Excludant (or MEX) of this set is , where is the ordinal limit of the natural numbers.
Now that we have a basic understanding of how the MEX works, let us take a look at how MEX helps us in calculating the Grundy number () next.
How to calculate Grundy Number?
The calculation of the Grundy Number is based on the following statement: The Grundy Number is equal to 0 for a game that is immediately lost by the player who plays first, otherwise, the Grundy Number is equal to the MEX of all the numbers which are possible next positions by making one move in the game.
Let us take a look at an example to see how we can calculate the Grundy Number.
The game will start with a pile of N coins and two players. The player whose turn is first may move any number of positive coins. The last player to move any number of coins wins the game. Before moving onto some cases, for simplicity, we'll say that the is written as .
Let us take a look at some cases:
Let N be the number of coins in the pile.
-
N = 0 : If the pile has 0 coins then the first player has nothing to pick and loses the game immediately, thus,
=
-
N = 1 : If the pile has 1 coin then he has the following one option :
- The player picks 1 coin, then 0 coins are left whose Grundy value is G(0)=0.
= = = .
-
N = 2 : If the pile has 2 coin then he has the following options :
- The player picks 1 coin, then 1 coin is left whose Grundy value is G(1)=1.
- The player picks 2 coin, then 0 coins are left whose Grundy value is G(0)=0.
= = = .
-
N = 3 : If the pile has 3 coin then he has the following options :
- The player picks 1 coin, then 2 coins are left whose Grundy value is G(2)=2.
- The player picks 2 coin, then 1 coin is left whose Grundy value is G(1)=1.
- The player picks 3 coin, then 0 coins are left whose Grundy value is G(0)=0.
= = = .
-
N = 4 : If the pile has 4 coin then he has the following options :
- The player picks 1 coin, then 3 coins are left whose Grundy value is G(3)=3.
- The player $picks 2 coin, then 2 coins are left whose Grundy value is G(2)=2.
- The player picks 3 coin, then 1 coin is left whose Grundy value is G(1)=1.
- The player picks 4 coin, then 0 coins are left whose Grundy value is G(0)=0.
= = = .
-
N = 5 : If the pile has 5 coin then he has the following options :
- The player picks 1 coin, then 4 coins are left whose Grundy value is G(4)=4.
- The player picks 2 coin, then 3 coins are left whose Grundy value is G(3)=3.
- The player picks 3 coin, then 2 coins are left whose Grundy value is G(2)=2.
- The player picks 4 coin, then 1 coin is left whose Grundy value is G(1)=1.
- The player picks 5 coin, then 0 coins are left whose Grundy value is G(0)=0.
= = = .
Let us formulate the size of the pile with its corresponding Grundy Number and try to find if it follows some pattern or not.
| Size of the pile (N) | Grundy Number (Grundy(N)) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
From the above table, it can be easily observed that for any its corresponding Grundy Number that is or is .
Also, note that the problem that we just discussed above is actually the Standard Game of Nim. Therefore just like the way we (Exclusive-OR) the Grundy Number of the size of piles to solve Standard Game of Nim we will use the same method over here but before we do that let us find the Grundy Number for Advanced Nim game(Zero Move Nim game).
Approach
We'll first try to find the Grundy Number (Grundy(N)) for some simple values of N, where N is the size of a pile of coins.
For simplicity, we will call the move of picking zero coins as zero moves and,
is the Grundy Number of N that is . nF as the pile of size N with no zero moves left. nT as the pile of size N with zero moves left ( we can reach the state of nF from nT for a value of n but the reverse is not possible since we can only use the zero move once).
Also, we should note that Grundy(N) is actually equivalent to Grundy(nT), thus for every N, its corresponding Grundy number will be Grundy(nT).
Let us look at some cases now:
- N = 0 : If the pile has 0 coins then the first player has nothing to pick and loses the game immeditely,thus, =
Note: We cannot pick 0 coin because the zero move is defined that it can only be applied to a pile having non zero coins.
-
N = 1 : There are two cases in this:
- nF = 1 : Pile of size 1 with no zero move left:
- The player picks 1 coin, then 0 coins are left. = =
- nT = 1 : Pile of size 1 with zero move left:
- The player picks 1 coin, then 0 coins are left.
- The player make the zero move and does not pick any coin, this new state is now 1F (pile of size 1 with no zero move left) = = = =
Therefore, = =
- nF = 1 : Pile of size 1 with no zero move left:
-
N = 2 : There are two cases in this:
- nF = 2 : Pile of size 2 with no zero move left:
- The player picks 2 coin, then 0 coins are left.
- The player picks 1 coin, then 1 coins are left, this new state is now 1F (pile of size 1 with no zero move left). = = = =
- nT = 2 : Pile of size 2 with zero move left:
- The player picks 2 coin, then 0 coins are left.
- The player picks 1 coin, then 1 coin is left, this new state is now 1T (pile of size 1 with zero move left).
- The player make the zero move and does not pick any coin, this new state is now 2F (pile of size 2 with no zero move left) = = = =
Therefore, = =
- nF = 2 : Pile of size 2 with no zero move left:
Note: We cannot create the state 1F(pile of size 2 with no zero move left) from the current state that is 2T because we would have to make two different moves i.e., pick 1 coin from the pile and make a zero move while we are allowed to make only one move.
-
N = 3 : There are two cases in this:
- nF = 3 : Pile of size 3 with no zero move left:
- The player picks 3 coin, then 0 coins are left.
- The player picks 2 coin, then 1 coins are left, this new state is now 1F (pile of size 1 with no zero move left).
- The player picks 1 coin, then 2 coins are left, this new state is now 2F (pile of size 2 with no zero move left). = = = =
- nT = 3 : Pile of size 3 with zero move left:
- The player picks 3 coin, then 0 coins are left.
- The player picks 2 coin, then 1 coins are left, this new state is now 1T (pile of size 1 with zero move left).
- The player picks 1 coin, then 2 coin is left, this new state is now 2T (pile of size 2 with zero move left).
- The player make the zero move and does not pick any coin, this new state is now 3F (pile of size 3 with no zero move left) = = = =
Therefore, = =
- nF = 3 : Pile of size 3 with no zero move left:
-
N = 4 : There are two cases in this:
- nF = 4 : Pile of size 4 with no zero move left:
- The player picks 4 coin, then 0 coins are left.
- The player picks 3 coin, then 1 coins are left, this new state is now 1F (pile of size 1 with no zero move left).
- The player picks 2 coin, then 2 coins are left, this new state is now 2F (pile of size 2 with no zero move left).
- The player picks 1 coin, then 3 coins are left, this new state is now 3F (pile of size 3 with no zero move left). = = = =
- nT = 4 : Pile of size 4 with zero move left:
- The player picks 4 coin, then 0 coins are left.
- The player picks 3 coin, then 1 coins are left, this new state is now 1T (pile of size 1 with zero move left).
- The player picks 2 coin, then 2 coins are left, this new state is now 2T (pile of size 2 with zero move left).
- The player picks 1 coin, then 3 coin is left, this new state is now 3T (pile of size 3 with zero move left).
- The player make the zero move and does not pick any coin, this new state is now 4F (pile of size 4 with no zero move left) = = =
Therefore, = =
- nF = 4 : Pile of size 4 with no zero move left:
-
N = 5 : There are two cases in this:
- nF = 5 : Pile of size 5 with no zero move left:
- The player picks 5 coin, then 0 coins are left.
- The player picks 4 coin, then 1 coins are left, this new state is now 1F (pile of size 1 with no zero move left).
- The player picks 3 coin, then 2 coins are left, this new state is now 2F (pile of size 2 with no zero move left).
- The player picks 2 coin, then 3 coins are left, this new state is now 3F (pile of size 3 with no zero move left).
- The player picks 1 coin, then 4 coins are left, this new state is now 4F (pile of size 4 with no zero move left). = = = =
- nT = 5 : Pile of size 5 with zero move left:
- The player picks 5 coin, then 0 coins are left.
- The player picks 4 coin, then 1 coins are left, this new state is now 1T (pile of size 1 with zero move left).
- The player picks 3 coin, then 2 coins are left, this new state is now 2T (pile of size 2 with zero move left).
- The player picks 2 coin, then 3 coins are left, this new state is now 3T (pile of size 3 with zero move left).
- The player picks 1 coin, then 4 coin is left, this new state is now 4T (pile of size 4 with zero move left).
- The player make the zero move and does not pick any coin, this new state is now 4F (pile of size 4 with no zero move left) = = =
Therefore, = =
- nF = 5 : Pile of size 5 with no zero move left:
Let us now formulate the size of the pile with its corresponding Grundy Number and try to find if it follows some pattern or not.
| Size of the pile (N) | Grundy Number (Grundy(N)) |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 1 |
| 3 | 4 |
| 4 | 3 |
| 5 | 6 |
From the above table, it can be easily observed that for any its corresponding Grundy Number that is is either if is odd or if is even, i.e.
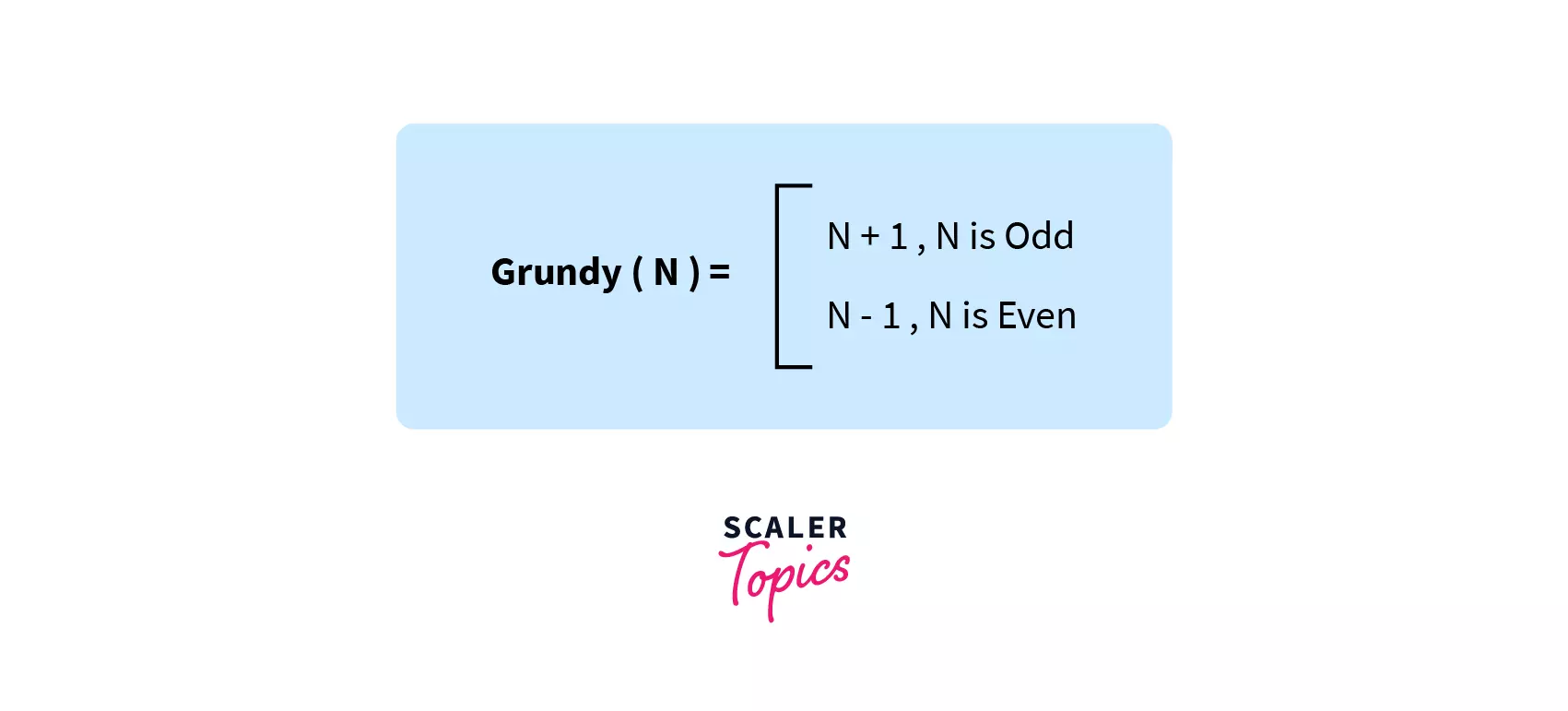
Now that we have the formula to find the Grundy number of any state (that is G(N)), let us move forward to define the Winning State and the Losing State of the game.
Winning State and Losing State
As we have noticed and pointed out above that this game is very analogous to the Standard Game of Nim (Nim Game), we shall be using a similar method of using the Cumulative XOR(Nim Sum) to define the winning state (Winner of the game) and the losing state (Loser of the game). We shall only talk about the player whose going to play first when we talk about the Winning state or losing state.
For an array Piles[] which represents the sizes of the pile of coins,
Winning State
Considering both the players play optimally, which means that they don’t make any moves that may hamper their chances of winning, then the player to play first will win the game if and only if the Cumulative XOR(Nim Sum) of the Grundy Number of the size of the piles is Non-zero.
Losing State
Otherwise, the player to play first will lose the game if and only if the Nim Sum of the Grundy Number of the size of the piles is Zero.
Example
Let us take a look at some examples before implementing the code.
Example 1:
Given piles of coins are:
Input:
= {, , }
Output:
Player 1 wins the game.
Explanation: Let us first calculate the equivalent Grundy number for each pile = {}
Now we calculate the Nim Sum(Cumulative XOR)
= (3^8^6) =
Since the Nim sum is Non-Zero, Player 1 wins the game, Let us take a look at another example before moving forward.
Example 2:
Given piles of coins are:
Input:
= {, , }
Output:
Player 2 wins the game.
Explanation: Let us first calculate the equivalent Grundy number for each pile = {}
Now we calculate the Nim Sum(Cumulative XOR)
= (9^3^10) =
Since the Nim sum is Zero, Player 2 wins the game.
Let us now look at the implementation of the above logic.
Implementation in C++
Output
Time and Space Complexity
The Time Complexity of the above defined solution is where n is the size of the piles' array. However, the auxiliary space complexity is , since no additional space has been used as we just need one variable to store the Nim sum(cumulative XOR).
Summary
- The Advanced Game of Nim is a slight modification over the Standard Nim Game.
- In Advanced Game of Nim, for each non-empty pile, either of the players can remove zero items and be counted as its move, but this move can only be used once per pile by either of the players.
- MEX or Minimum Excludant is the smallest non-negative number not present in a set of numbers.
- A Grundy Number is a number that defines a state of a combinatorial game.
- The Grundy Number is equal to:
- 0 for a game that is immediately lost by the player who plays first, else,
- the MEX of all the numbers which are possible next positions by making one move in the game.
- =
- , if N is odd,
- , if N is even.
- The player to play first will win the game if the Cumulative XOR(Nim Sum) of the Grundy Number of the size of the piles is Non-zero.
- The player to play first will lose the game if the Cumulative XOR(Nim Sum) of the Grundy Number of the size of the piles is Zero.
- The Time Complexity of the above defined solution is and the auxiliary space complexity is where n is the size of the piles[] array.
