Binary Search Algorithm

Overview
Binary search is an efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing in half the portion of the list that could contain the item, until you've narrowed down the possible locations to just one.
Takeaways
- Complexity of Binary search algorithm
- Time complexity - O()
- Space complexity - O(1)
This is the second part of a three-part series on Searching Algorithms.
In the previous article, Linear Search, we discussed why searching is so important in everyday life and discussed the most basic approach to perform searching; Linear Search. If you didn’t get a chance to read that one, I’d highly recommend jumping right to it and have a quick read.
Today, we will be discussing an approach which frankly is personally my favorite algorithm of all time; Binary Search.
Definition
A quick recap on the definition of searching.
Searching is a method to find some relevant information in a data set.
While discussing the Linear Search algorithm, we mentioned that it is not very efficient as in most cases, as it ends up searching the entire array to find an element.
Since it wasn’t the most practical approach for large data sets, we desperately needed an improvement over it and the programming geniuses worked hard to find one. And they did 🙂
In a galaxy very very near, Binary Search was born.
Binary Search
Binary Search is an algorithm that can be used to search an element in a sorted data set. By sorted, we mean that the elements will either be in a natural increasing or decreasing order.
Natural order is the default ordering of elements. For example, integers’ natural increasing order is 1, 2, 3, 4, … which is the increasing order of their value.
A: 5 3 12 38 9 45 1 22 3
B: 1 3 3 5 9 12 22 38 45
In the above example, the array A is not sorted as the elements are not in either natural increasing or decreasing order of value. While the array B is sorted in natural increasing order.
In a nutshell, we can say that an array of integers is sorted if
where size is the number of elements in the array.
Similarly for strings, in programming, the natural order is lexicographic, or simply, how you would find them in an English dictionary.
For example, “ant” will be present before “art” in an English dictionary. Thus, “ant” is said to be lexicographically smaller than “art”.
Let’s say we’re trying to search for a number, K, in a sorted array of integers. For simplicity, let’s assume the array is sorted in natural increasing order.
Let’s say the array is
1 3 3 5 9 12 22 38 45
And the element we’re searching for, K = 12
If we apply Linear Search, we will always start with the first element until we either find K or reach the end of the array.
But since the array is sorted here, can we use that to our advantage?
Let’s make an acute observation.
In a sorted array, for any index i, where 0 <= i < size and size is the number of elements in the array
if arr[i] < K
It means the element at index i is less than K. Hence, all the elements before the index i will also be less than K right, since the array is sorted. Therefore, we can choose to ignore the elements on the left side of the index i and not compare them with K at all.
For example, if i = 2, arr[2] = 5. Hence, arr[2] < K, so we ignore the elements on the left side of index i, i.e. 1 and 3 since they will also be less than K and we will never find 12 on that side.
1 3 3 5 9 12 22 38 45 K = 12
1 3 3 5 9 12 22 38 45 K = 12

Similarly,
if arr[i] > K
It means the element at index i is greater than K. Hence, all the elements after the index i will also be greater than K right, because of the sorted nature of the array. Thus, we can choose to ignore the elements on the right side of index i and not compare them with K at all.
For example, if i = 5, arr[5] = 12. Hence, arr[5] > K, so we ignore the elements on the right side of index i, i.e. 22, 38 and 45 since they will also be greater than K and we will never find 12 on that side.
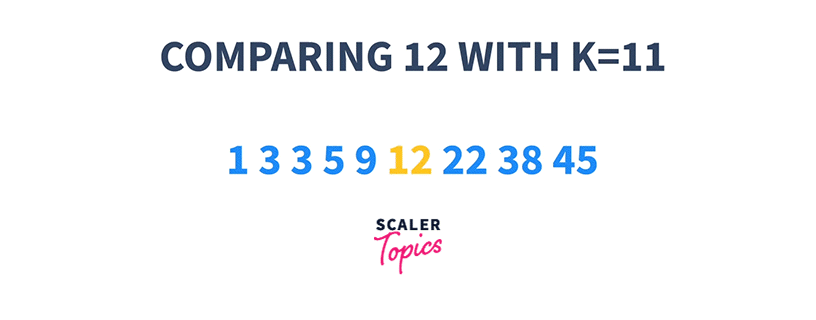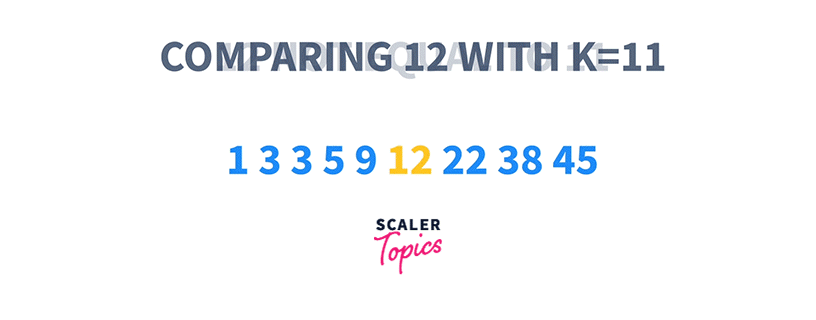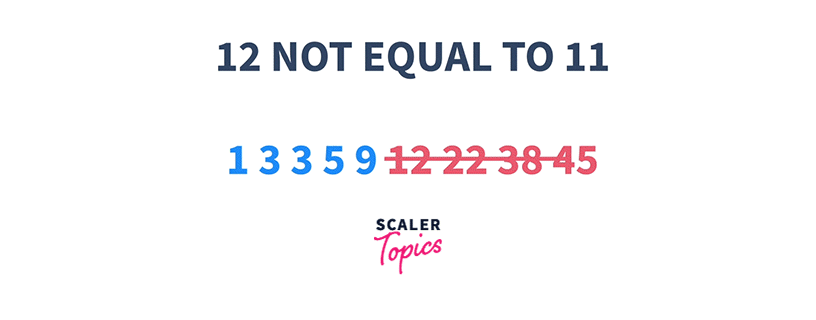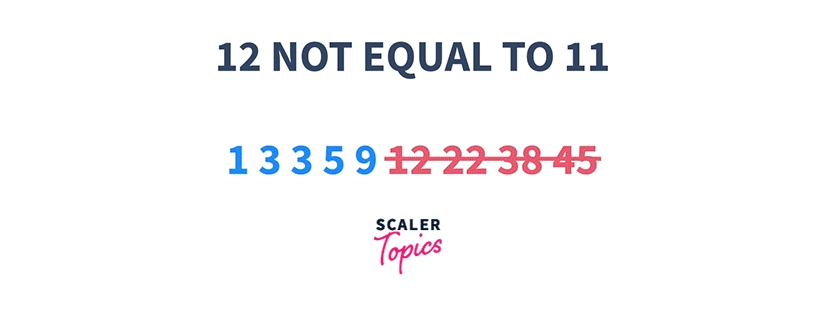
1 3 3 5 9 12 22 38 45 K = 11
1 3 3 5 9 12 22 38 45 K = 11
That means if we start searching at any index i, and check if the element at that index is either less than or greater than K, we can choose to ignore a particular set of elements present on the left or the right side of that index respectively.
On the other hand,
if arr[i] == K
It means that the element at index i is equal to K and we have found the element K in the array. Hence, we do not need to search any further and our job is done.
If we choose the right position to start searching, the above observation can reduce the number of elements we need to search by quite a big margin.
Now comes the problem of choosing the most optimal position to start the search from. That’s where the term ”Binary” comes into the picture.
Unary means one. Binary means two.
If you’re thinking about starting at the middle of the array, you’re absolutely 100% right.
Binary Search works on the principle of Divide and Conquer. It divides the array into two halves and tries to find the element K in one or the other half, not both. It keeps on doing this until we either find the element or the array is exhausted.
We start the search at the middle of the array, and divide the array into binary, or two parts. If the middle element is less than K, we ignore the left half and apply the same technique on the right half of the array until we either find K or the array cannot be split any further.
Similarly, if the middle element is greater than K, we ignore the right half and apply the same technique on the left half of the array until we either find K or the array cannot be split any further.
Let’s try to apply this approach for the above example.
The size of the above array is, size = 9
Thus, the middle element will be at index i = (9 – 1) / 2 = 4
We will start with the middle element, at index i =4 and K = 12
1 3 3 5 9 12 22 38 45 9 < 12, ignore left half
1 3 3 5 9 12 22 38 45 22 > 12, ignore right half
1 3 3 5 9 12 22 38 4 12 == 12, found K

As you can see above, we found K = 12 in just the third comparison. This is better than the linear search approach where it would’ve taken five comparisons.
Let’s try another example where K might not be present in the list, K = 4.
1 3 3 5 9 12 22 38 45 9 > 4, ignore right half
1 3 3 5 9 12 22 38 45 3 < 4, ignore left half
1 3 3 5 9 12 22 38 45 3 < 4, ignore left half
1 3 3 5 9 12 22 38 45 5 > 4, ignore right half
1 3 3 5 9 12 22 38 45 no more elements left to compare

As you can see, we could not find K since it was not present in the array. But we were able to determine this is just 4 comparisons, while linear search would’ve compared all the elements of the array.
You: But Rahul, this just took 5 less comparisons. All this effort for a measly 5 comparisons :/
Rahul: Yes for the above example, it might look like it’s not a very big optimization over linear search. But that’s because the number of elements in the array is quite less, very less to be precise. The real power of binary search can be seen when the array contains millions of elements.
You: How much exactly? Like 10 comparisons less than linear search? 😛
Rahul: Haha. Nice one. Keep reading to find out 🙂
Algorithm
Below is the algorithm of Binary Search.
- Initialise n = size of array, low = 0, high = n-1. We will use low and high to determine the left and right ends of the array in which we will be searching at any given time
- if low > high, it means we cannot split the array any further and we could not find K. We return -1 to signify that the element K was not found
- else low <= high, which means we will split the array between low and high into two halves as follows:
- Initialise mid = (low + high) / 2, in this way we split the array into two halves with arr[mid] as its middle element
- if arr[mid] < K, it means the middle element is less than K. Thus, all the elements on the left side of the mid will also be less than K. Hence, we repeat step 2 for the right side of mid. We do this by setting the value of low = mid+1, which means we are ignoring all the elements from low to mid and shifting the left end of the array to mid+1
- if arr[mid] > K, it means the middle element is greater than K. Thus, all the elements on the right side of the mid will also be greater than K. Hence, we repeat step 2 for the left side of mid. We do this by setting the value of high = mid-1, which means we are ignoring all the elements from mid to high and shifting the right end of the array to mid-1
- else arr[mid] == K, which means the middle element is equal to K and we have found the element K. Hence, we do not need to search anymore. We return mid directly from here signifying that mid is the index at which K was found in the array
Below is an implementation of Binary Search in Java 8 –
Output:
Time Complexity
Since we always start with the middle element first, in the best case, it’s possible that the middle element of the array itself is the element we’re searching for, K.
On the other hand, if the element we’re searching for is not present in the array, we keep splitting the array into two halves until it cannot be split any further, i.e. only one element is left. So what is the complexity of this?
Let’s solve this with an example. Assume the size of the array is N = 8.
- In the first step, the array of size 8 is split in the middle into two parts of size 4 each.
1 2 3 4 | 5 6 7 8
- In the second step, either of the two arrays of size 4 is split in the middle into two parts of size 2 each.
1 2 | 3 4 or 5 6 | 7 8
- In the third step, either of the four arrays of size 2 is split in the middle into two parts of size 1 each.
1 | 2 or 3 | 4 or 5 | 6 or 7 | 8
Now, we will be left with only one element which cannot be split any further.
If you notice, at each step, we are discarding one half of the array, until we either find the element or there are no more elements left to search in.
So we conclude that the worst-case time complexity will be the total number of steps in which we can split the array into two halves until it cannot be split any further.
In the above example, it took 3 steps to split the array into two halves until only one element was left.
Let’s try to generalize this. Did you notice something?
N = 8 =
Taking logarithm with on both sides,
= = = 3
Since = 1,
= 3, total number of steps to split N into 2 halves until it’s equal to 1
This is exactly like the definition of logarithm: gives us the value of the exponent to which we must raise the base (2 in our case) to produce x (which is the size of the array in our case).
Hence, for an array of size N, it will take steps to split it into two halves until only one element is left.
Since the length of the array was a power of 2 in the above example, the value of is an integer. But if it is not a power of 2, will be a decimal value. Hence, we can take the ceiling value of in general.
The ceiling value of any number x is the minimum integer value that is greater than x. For example, the ceiling value of 2.5 will be 3.
By applying some basic high school mathematics here, we were able to conclude that for an array of size N, the worst-case time complexity of binary search will be O(ceil()).
To give you some perspective, if N = 100000 (), the worst-case complexity of linear search will be O(N) = O().
Not that good right?
On the other hand, the worst-case complexity of binary search will be
= O ( ) = O(16.6096404744) ~ O(17)
That means the binary search will be able to determine whether an element is present in an array or not in just 17 steps. It’s almost 6000 times better than a linear search.
Mind-blowing right? 😛
Space Complexity
As we can see we are not using any significant extra memory in Binary Search. So the space complexity is constant, i.e. O(1).
P.S. The variables used for storing the bounds, middle index and other minor information are constant since they don’t depend on the input size of the array.
Applications of Binary Search
If the array is sorted, binary search is the clear winner. It takes in the worst case while linear search will take O(N) in the worst case.
You: But what if the array is not sorted, Rahul? We won’t be able to use this awesome algorithm after all.
Rahul: Yes you are right. If the array is not sorted, we won’t be able to use binary search directly. Yikes! We can always sort the array and then apply binary search 😀
You: But sorting itself might take O(N*) and then an additional for binary search. This is even worse than linear search .
Rahul: I’m glad you mentioned that :)
You’re absolutely right though. If we have to sort the array, then the total time complexity of sorting and binary search will be even more than that of linear search. In that case, a linear search might be the best solution.
But if you are given an array and you have to perform multiple, let’s say Q search queries on it. Then binary search is your best friend.
Why?
Because once we sort the array, then we can perform all the queries one by one on the sorted array. And since, each binary search query will only take time in the worst case, for Q queries it will take *O(Q)**.
So if we use a good sorting algorithm like Merge Sort or Heap Sort which has a guaranteed time complexity of *O(N)**, the total time complexity will be
Binary Search = O(N + Q) = O((N+Q) * )**
If we assume the number of queries to be equivalent to the number of elements in the array, then the above equation becomes
Binary Search = O(N * )
On the other hand, if we use a linear search, then each query will take O(N) in the worst case and the total time complexity for Q queries will be
Linear Search = O(N * N) = O()
As we can see, binary search performs a lot better than linear search if the array is not sorted and the number of queries is huge, which is the more likely scenario in real-life use cases.
Conclusion
Today we learned an absolute legend of an algorithm. Binary search has a whole lot of applications, other than search as well.
Food for thought: It can be used to find the square root of a number as well 😛
Thanks for reading. May the code be with you 🙂
Exercise
- We mentioned that binary search can be used to find the square root of a number. Can you think about how we can do it? If you would like to solve this question, you can find it here on InterviewBit
- We have implemented the iterative solution of binary search above. Try writing a recursive version of it yourself. And think about which one has a better performance in terms of time and space complexity
- Binary search is one of the hottest topics in interview questions. Here is one such question.
