Bit Masking

A bit is a boolean value that can be either 0 or 1. Bitmasking is the act of applying a mask over a value to keep, change or modify a piece of given information. A mask determines which bits to take and which bits to clear off a binary number. Bitmasking can be used to mask a value to represent the subsets of a set using various bitwise operations. The concept of bitmasking is used along with dynamic programming to solve a wide range of problems.

In this article, we will discuss bitmasking and also solve problems involving Bitmasking and Dynamic Programming.

Scope of the Article

• This article defines Bit Masking and explains the intuitive logic of this algorithm.
• We learn to generate all the subsets of a set with bit masking along with its C++ implementation.
• We also discuss a problem in which we have shown the implementation of Bitmasking with Dynamic Programming.

Takeaways:

Bit masks are used to access specific bits in a byte of data. This is often useful as a method of iteration.

What is Bit Masking?

A bit is a boolean value that can be either 0 or 1. In computing whenever we use a number they are internally processed as a summation of 0's and 1's. For example, the number 5 is represented as 101 in binary.

Masking is a general concept in which we keep, change, or remove some part of the information.

In programming, a mask determines which bits we want to keep and which bits we want to clear off a binary number. Masking is the act of applying masks to a value using various bitwise operations. Masks can be imposed over a number to represent different information using a single value. One of the useful applications of bitmasking is to mask a number to represent the subsets of a set.

Let us understand how we can mask a value to represent a set using Bitmasking.

How Bitmasking is used to Represent a Set of Elements?

Let us suppose we have a set S consisting of N items numbered from 1 to N. Set S can be represented as follows, $S=1,2,3,\dots ,N$. Bitmasking is a way in which every subset of S can be represented with the help of a number in its binary form. To represent a set of N items we need a sequence of N bits where every bit represents an item in the Set. This sequence of bits used to represent a subset of a set is usually referred to as a mask. For example, the sequence of bits 10101 is a mask used to represent a set of size 5.

In a particular subset if the $i^{th}$ bit in the mask is set or is equal to 1 that means that the $i^{th}$ item is included in the subset. If the $i^{th}$ bit is unset or is equal to 0 that means that the $i^{th}$ item is not included in the subset. For example, the mask 1010110 represents a subset of a set having 7 items (number of bits in the mask) including items 2,3,5,7 (1 based indexing). Refer to the diagram shown below.

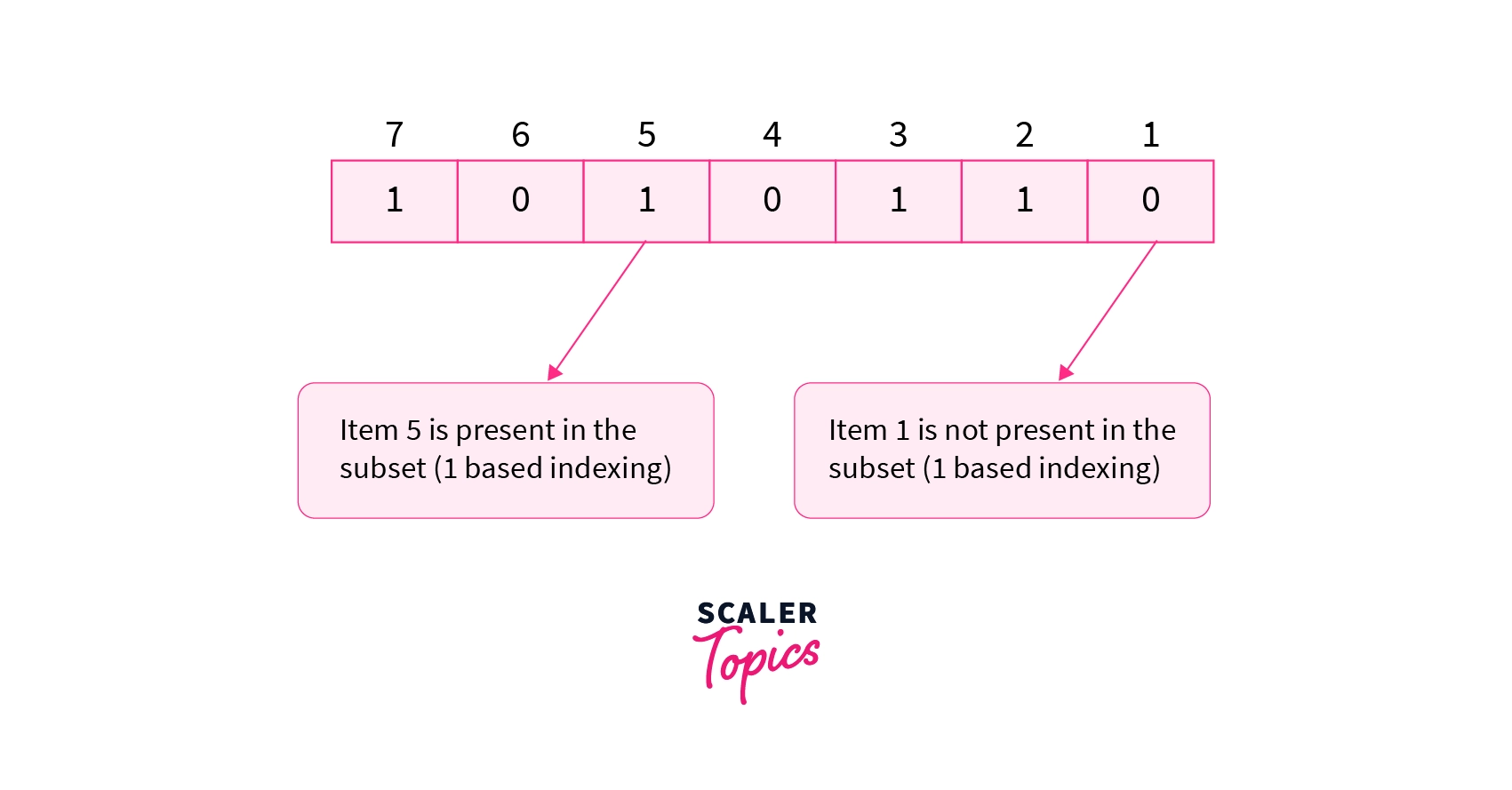
The mask represents a subset of a set having 7 items. The subset consists of only items 2,3,5,7(**1based indexing**) as the corresponding bits in the mask are set to1`.

Let us now understand how we can generate the subsets of a set using bit masking.

Generating Subsets of a Set using Bit Masking

A set of size N can have a maximum of $2^N$ subsets. Thus we need $2^N$ masks to represent all the subsets of a set.

If there is a set S consisting of 2 items, item1 and item2. We know that there will be $2^2$ subsets, i.e 4 subsets of set S. Let us now try to generate all the possible subsets of set S. We will also encode each subset with a unique mask. Refer to the diagram shown below.

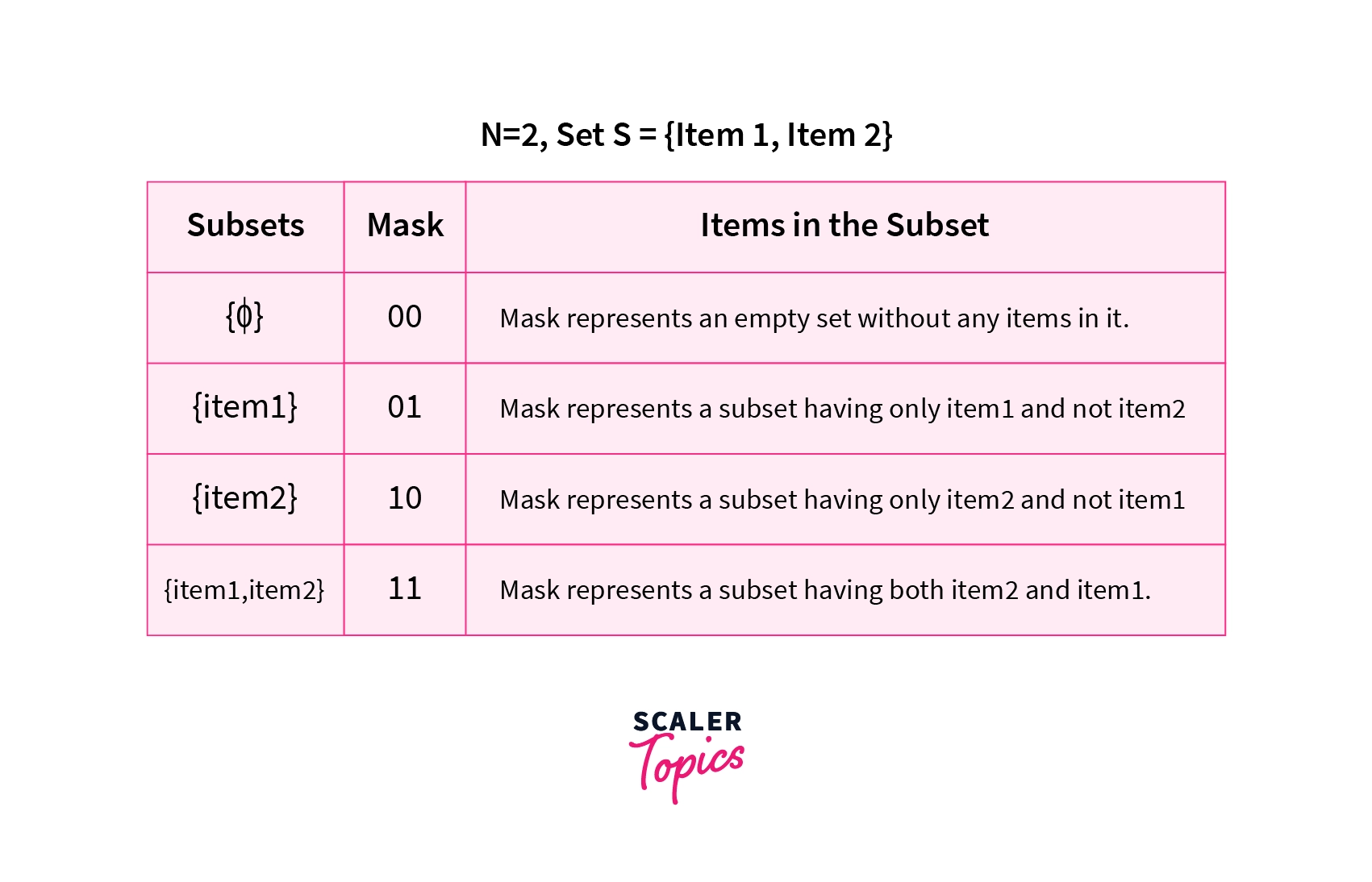
The table shows all the subsets of set S and also the masks associated with each subset

The diagram shown above shows all the subsets that are possible from the given set S. The masks {00,01,10,11} represent each subset of the set S. The mask 00 represents an empty set. The mask 01 represents a subset having only item1 and so on.

If we look carefully, we can see that these masks are equal to the binary representation of the number {0,1,2,3}. Thus to represent all the subsets of a set we use the numbers $0,1,2,\dots ,2^N-1$ in their binary forms. However, it is not necessary to explicitly convert these numbers in their binary forms as they will be converted to their binary form during the compilation of the code. Let us look at some of the basic bitwise operations.

Basic Bitwise Operations

In this section, we will look at some of the basic bitwise operations that we will use in the later parts of the article.

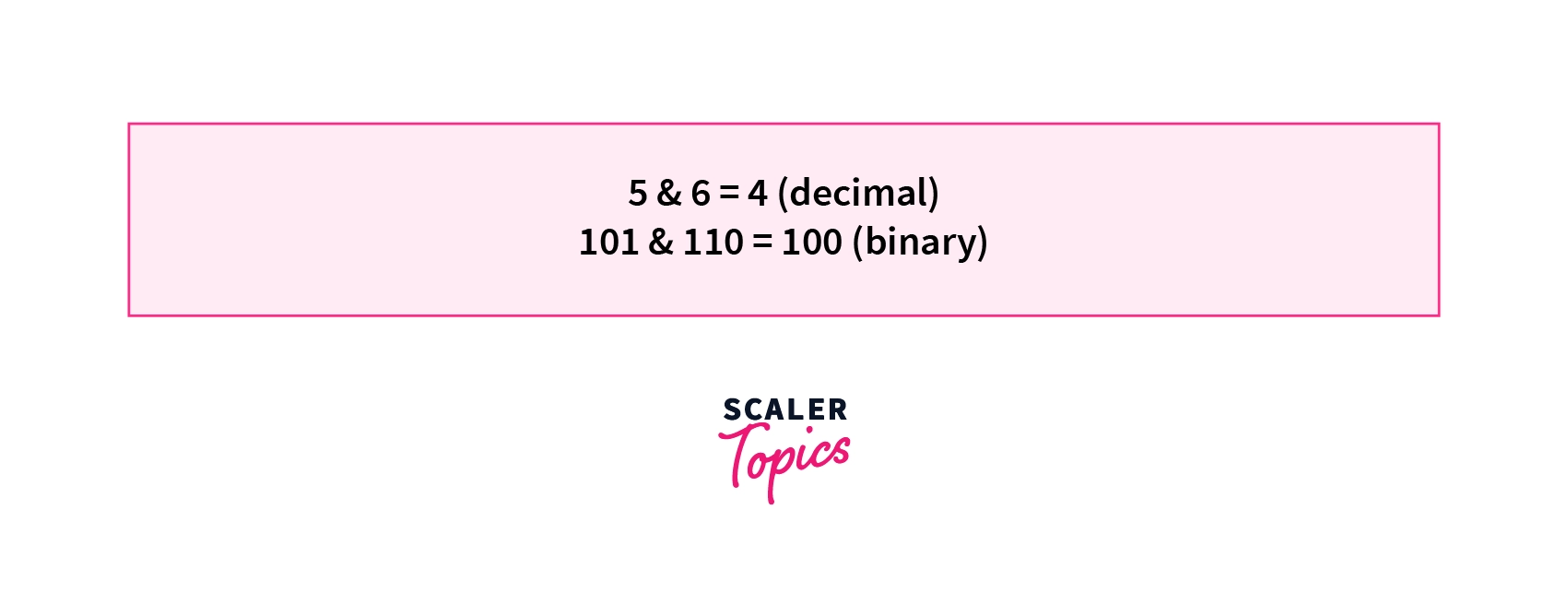
1. Bitwise And Operator & – The bitwise & of two bits is equal to 1 if the corresponding bits of both the operands are equal to 1. If either bit of an operand is 0 then the result is equal to 0.

2. Bitwise Or Operator | – The bitwise or of two operands is equal to 1 if at least one corresponding bit of both the operands is equal to 1.

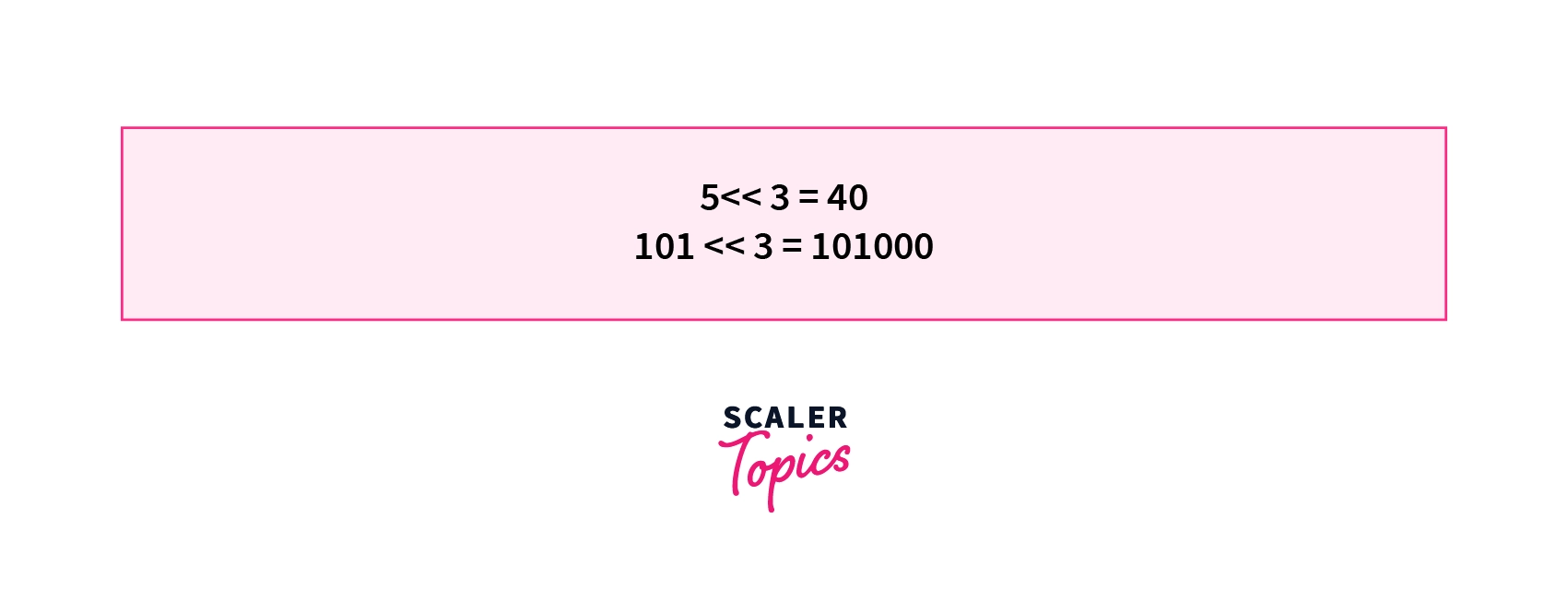
3. Left Shift Operator << – The left shift operator shifts all the bits of a particular number left by a specified number of bits. All the bits vacated by the left shift operation are filled with 0's. $5<<3$ will shift all the bits in the binary representation of 5 left by 3 places. $5<<3=(101000)2$=$(40){10}$.

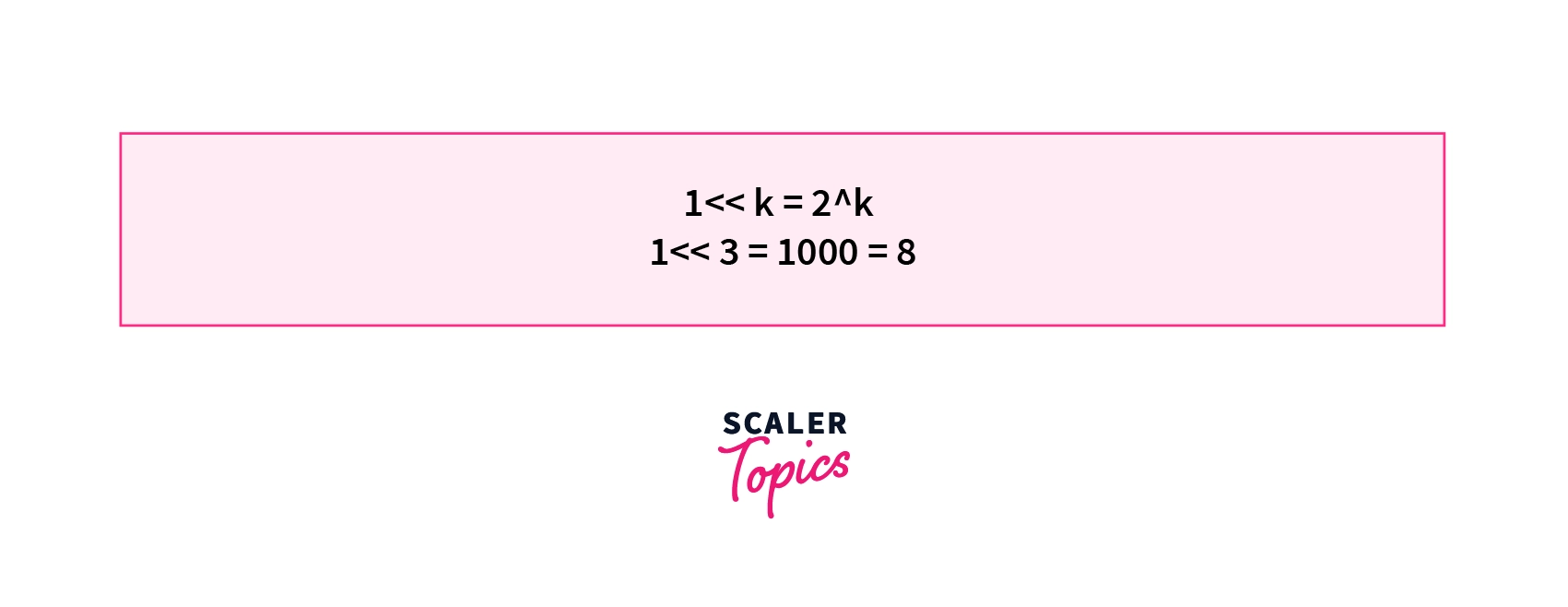
4. Power of 2 using << operator – One useful application of the left-shift operator is to find the power of 2. If we left-shift 1 by k places we will get the result $2^k$ in decimal. For example, $1<<1$ will result in $(10{)}_2$ which is equal to 2 in decimal. Similarly, $1<<3$ will result in $(1000{)}_2$ which is equal to 8 in decimal.

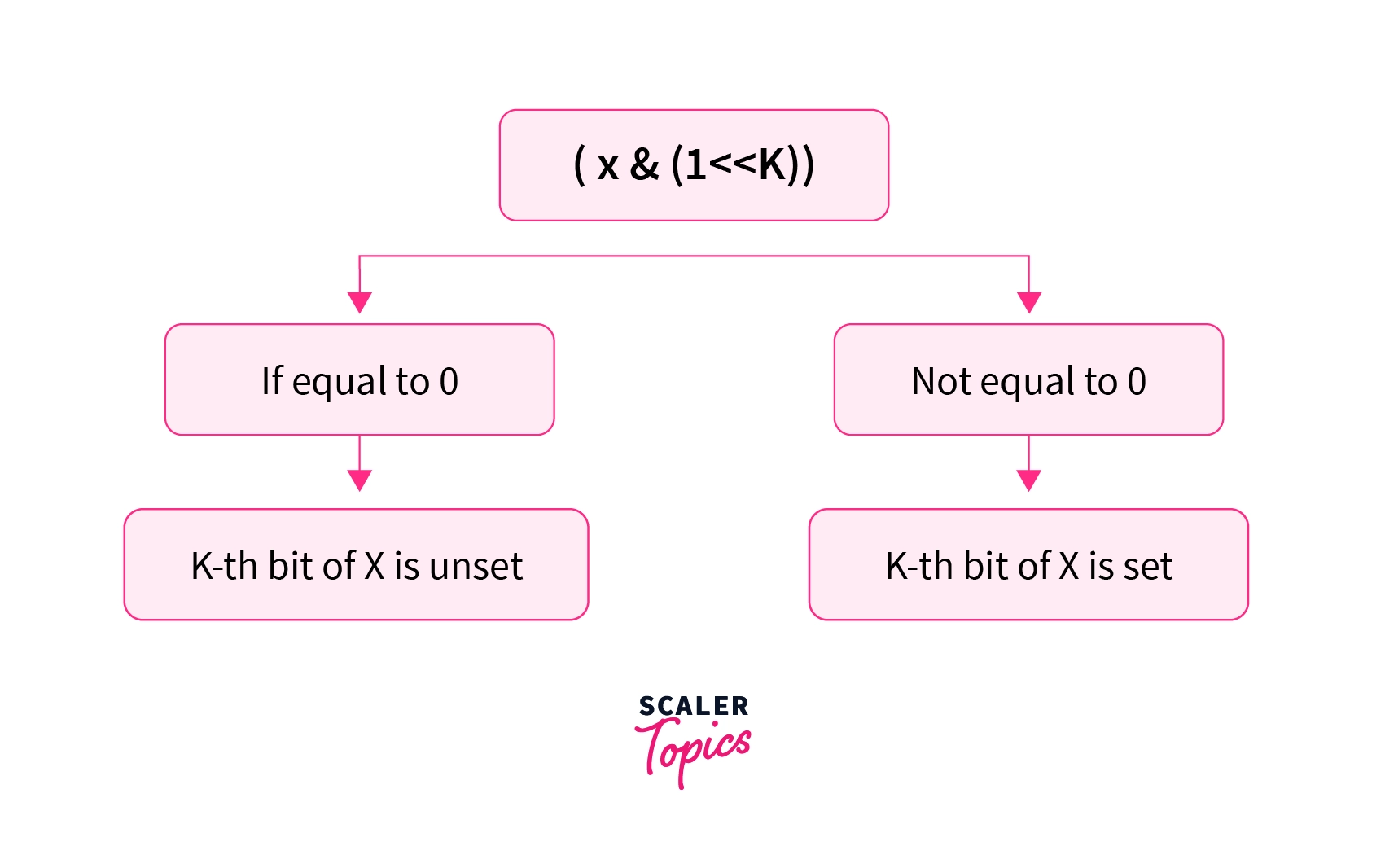
5. Checking if the $i^{th}$ bit is set or not – Let us take a binary number $X=(101101{)}_2$. If we want to check whether the 2nd bit from the right (0 based indexing) of X is set or not. We can left shift 1 by 2 places which will give us ${100}_2$ in binary and take its bitwise and & with X. If the result of bitwise & of X and $1<<2$ is equal to 0 that means that the $2^{nd}$ bit in X is unset or is equal to 0. Else the $2^{nd}$ bit of X is set or is equal to 1. In this case, we can see that 101101 & $00100$ = $(00100{)}_2$ which is not equal to 0. Hence the 2nd bit of X is set. We can generalize this idea to all the bits of X.

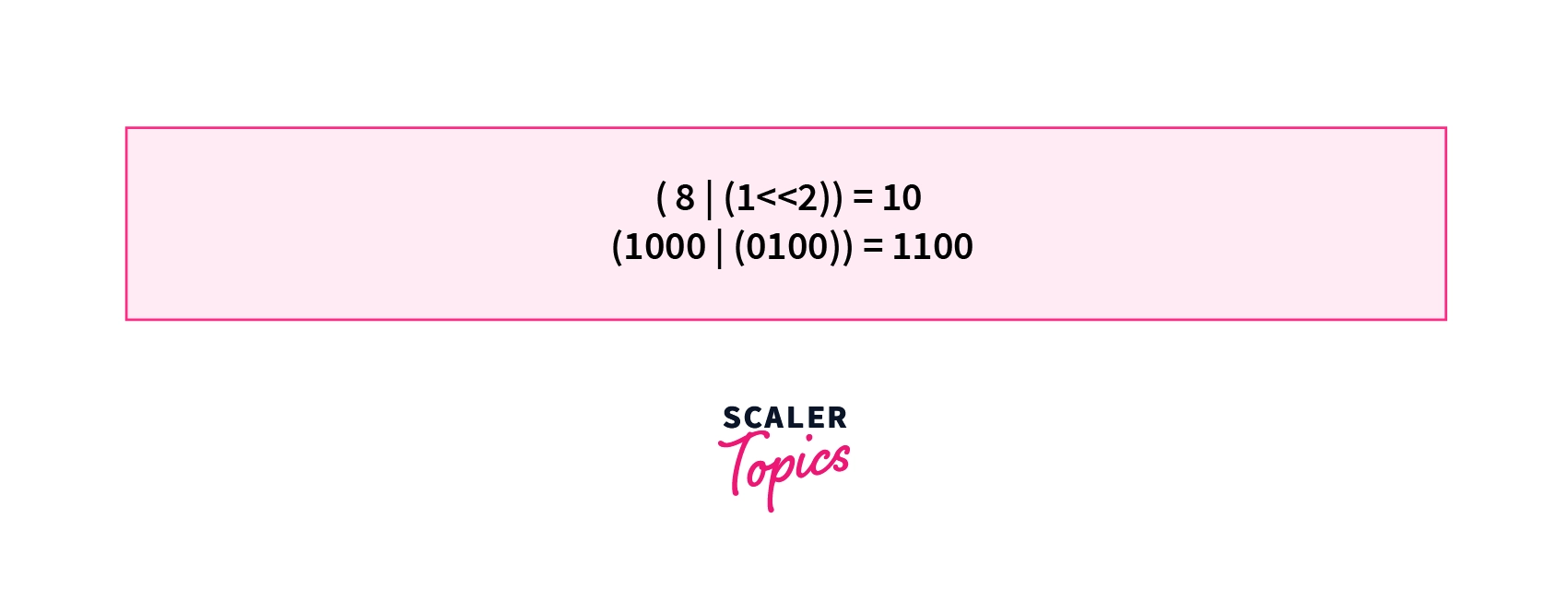
6. Set the $k^{th}$ bit of a number – We can use a similar idea discussed above to set a particular bit of a number. If we want to set the $k^{th}$ bit a number from right (0 based indexing) we can left shift 1 by k places and take its bitwise or with the number. If we want to set the $2^{th}$ bit of the number $(1000{)}_2$. We can do the operation $(1000|(1<<2))$ = $(1000|0100{)}_2$ = $(1100{)}_2$.

Now let’s try to implement the code for generating all the subsets of a given set using a bitmask.

Problem Statement 1

Given a set S of size N consisting of N items numbered from 1 to N. Print all the subsets of S. Set S can be represented as S= {1,2,3...,N}.

For a set of size equal to 2. All the possible subsets are {0},{1},{2},{1,2}. Where {0} represents an empty set.

Constraints-

• N can range from any integer between 1 to 20 inclusive. i.e $1<=N<=20$

Implementation of Generating All the Subsets of a set Using Bitmask.

As we have seen above that we can mask all the subsets of a set using the binary representation of a number from 0 to $2^{N-1}$. So we will run two loops. The outer loop will run through all the masks representing a particular subset of a set. That is the outer loop will run from 0 to $2^{N-1}$. In the inner loop, we will iterate through all the bits of a mask where each bit represents a specific item in the set. That is we will iterate from 0 to N-1 as there are N items in the set and each bit represents an item of the set.

If the $i^{th}$ (0 based indexing) bit of a mask is set that means that the $(i+1{)}^{th}$ (1 based indexing) item is present in the current subset. So we will print the $(i+1)$. Else we will continue the loop. At the end of the outer loop, we will get all the subsets of the given set S.

To check whether the $i^{th}$ bit of a mask is set or not we will use the algorithm discussed in the above section. Let us look at the code for the same.

C / C++ Implementation for Generating All the Subsets of a Set

// C / C++ code to print all the subsets of a Set 
// consisting of N items.

#include<bits/stdc++.h>
using namespace std;

void PrintAllSubsets(int N, int maximum_mask_required)
{
    //print the empty set or the null set seperately.
    cout << "0";

    //In the outer loop we will iterate through all the masks required
    // i.e from 0 to 2^N-1
    for (int mask = 0; mask <= maximum_mask_required; mask++)
    {
        //In the inner loop we will check whether the k-th bit of
        // the mask is set or not
               //If k-th bit is set k+1 th item is present in the subset
               // Else k+1-th item is not present in the current subset.
        for (int k = 0; k < N; k++)
        {
            if ((mask & (1 << k)) != 0)
            {
                // the k-th bit of the mask is set print k+1 (1 based indexing)
                cout << k + 1 << " ";
            }
        }
        cout << "\n";
    }
}

int main()
{

    int N = 3; // There N items in the set numbered from 1 to N

    int maximum_mask_required = (1 << N) - 1;// Maximum mask that will be required to represent a subset

    // Print all subsets of set S consisting of N items.
    PrintAllSubsets(N, maximum_mask_required);
    return 0;
}

Time Complexity

To generate all the subsets of a set S having N elements we run two loops. The outer loop runs from 0 to $2^{N-1}$. That is through all the masks required to represent all the subsets of size N . In the inner loop, we iterate through each bit in the mask. As there are N items in the set $S$ we iterate through $N$ bits in the inner loop from 0 to $N-1$. Thus the time complexity for the given approach is $O(2^N\ast N)$.

Bitmasking with Dynamic Programming

Till now we have discussed how bit masking can be used to represent a Set by only using a decimal integer. The concept of bit masking can be used along with dynamic programming to solve a wide range of problems.

We have seen that in bit masking we follow a brute-force approach in which we consider every possibility that we might come across. For example, in the subset generation problem, we considered all the subsets of a given set.

In the problems of bit masking that consist of Overlapping Subproblems, Dynamic Programming can be used to reduce the time complexity of the brute force approach by many folds.

In the dynamic programming approach, we store the results of an already calculated state to prevent calculating a particular subproblem multiple times. We would suggest everyone to refer to the article 0-1 Knapsack Problem where we have discussed dynamic programming from the basics.

Let us consider a problem that uses BitMasking along with Dynamic Programming.

Problem Statement 2

Given a set of N people and N tasks, you have to assign 1 task to exactly 1 person. This means that every person will be allotted only one task. We will also be given a Cost matrix where $Cost[i][j]$ will represents the cost of alloting $j^{th}$ task to the $i^{th}$ person (0 based indexing).

Out of all the possible combinations in which the tasks can be allotted, we have to assign the tasks in such a way that the total cost of assigning the tasks is maximized.

Constraints

• N can range from any integer between 1 to 20 inclusive. i.e $1<=N<=20$
• $1<=Cost[i][j]<=100$ where $0<=i<N$ and $0<=j<N$.

Consider the input shown in the diagram below-

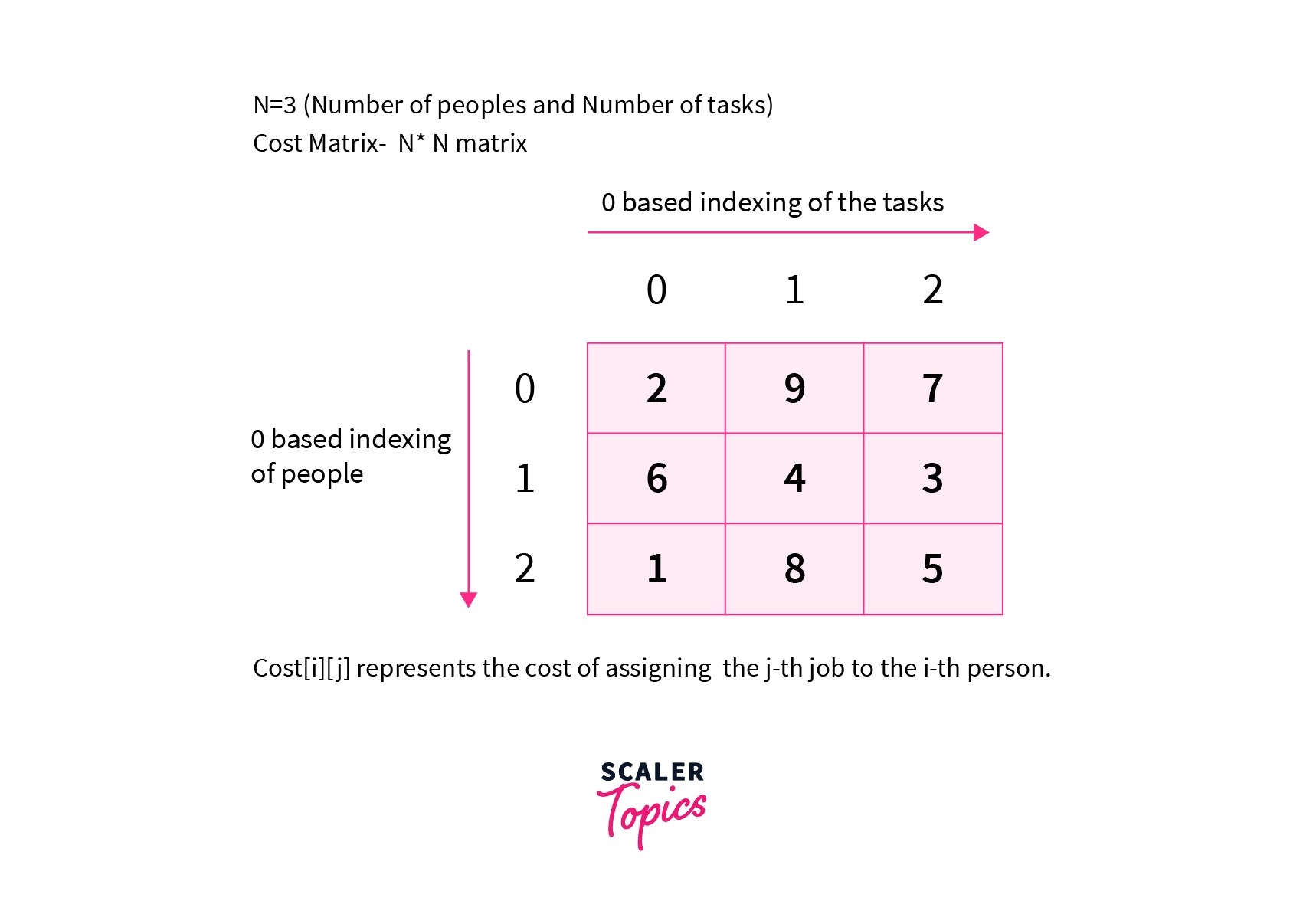
We are given N=3. This means that there are 3 people and 3 tasks respectively. The cost matrix shows the cost of assigning a task to each person.

Note that we can assign one task to exactly one person.

Optimal Solution

The optimal solution for the given input will be to assign the $3^{rd}$ task to the $1^{st}$ person, assign the $1^{st}$ task to the $2^{nd}$ person, and assign the $2^{nd}$ task to the $3^{rd}$ person. The total cost will be $cost[0][2]+cost[1][0]+cost[2][1]=7+6+8=21$.

Refer to the diagram below for a better understanding.

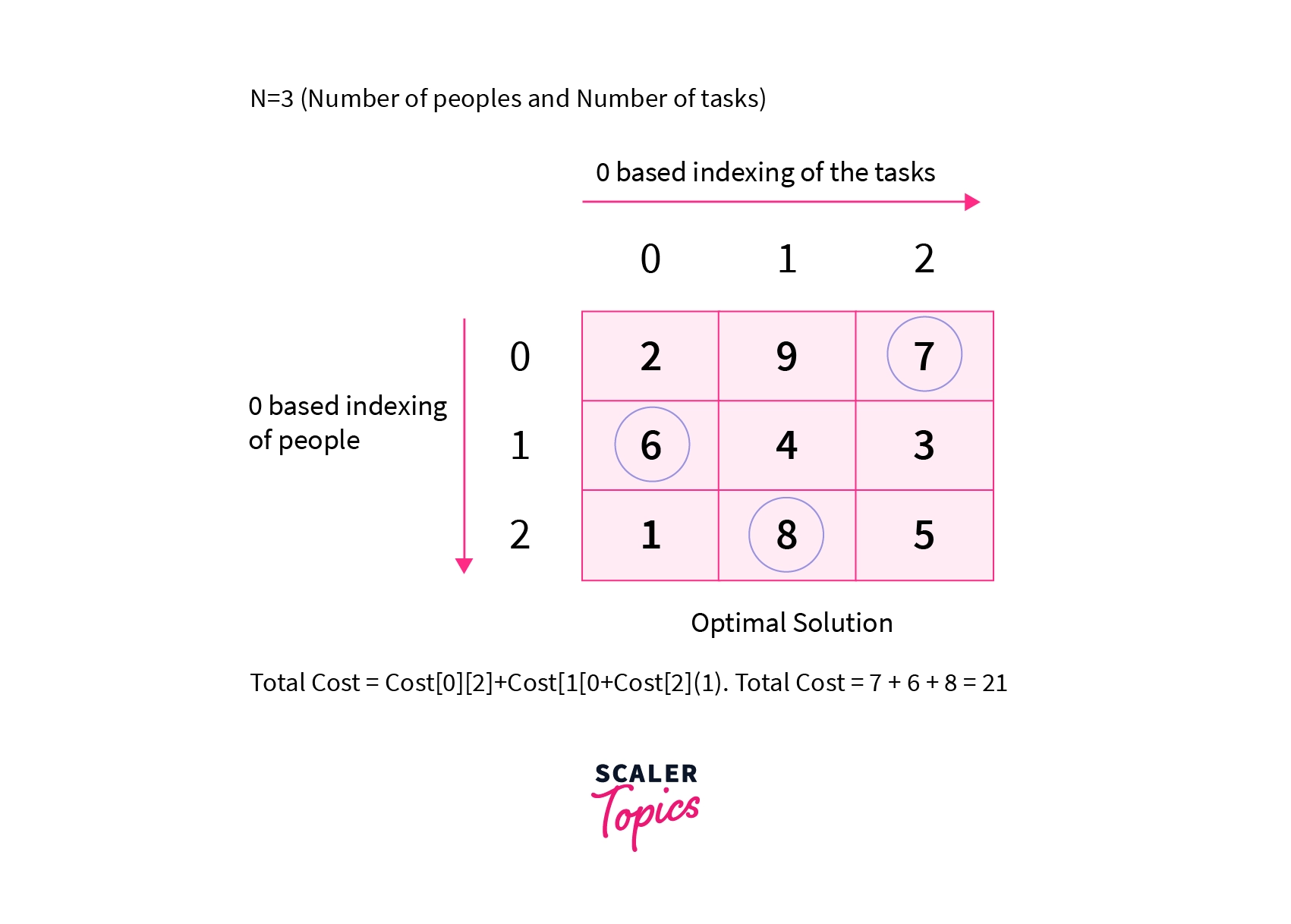
We can try all other valid combinations of assigning tasks but none will give a total cost greater than 21. Thus 21 is the required answer for the given input.

Creating the Algorithm for the Problem

To solve the above problem there are some key observations that we need to make. Let’s discuss them one by one.

• The constraint for N is very less. N can range from 1 to 20. In the problems that can be solved using bit masking, the constraints are generally less as they require an exponential time complexity. Though it does not always ensure that the problem can be solved using bit masking. The constraints give us a rough idea that the problem may be solved using bitmasking.
• Trying all the ways of assigning tasks and choosing the optimal answer from all the valid combinations. Here valid combinations mean that one person is assigned only one task. The fact that we need to try all the possible ways and find the optimal answer among them gives us a fair idea that the problem may be solved using dynamic programming.

Now we need to develop an algorithm by which we can try all the possible ways in an efficient way. We will use recursion to generate all the possible ways and find the maximum cost of assigning tasks. Later we will memoize this recursion with the help of Dynamic Programming which will optimize our recursion by many folds.

Trying All the Possible Ways Using Recursion

Now we will discuss the recursion to generate all the possible combinations. We will use 0 based indexing while referring to the jobs and to the people. Initially, we will assign the $0^{th}$ job and we have the set of people {0,1,2} available with us. Let us define a function Rec(i, S) which will determine that we are currently assigning task i and we have S set of people available with us.

For example, the state Rec(1,{0,2}) tells us that currently, we are assigning the $2^{nd}$ task (0 based indexing) and we have the $1^{st}$ and the $3^{rd}$ person available in our set to whom we can assign the $2^{nd}$ task.

We will try out every way of assigning the i-th task to the S set of people. Refer to the recursion tree shown below.

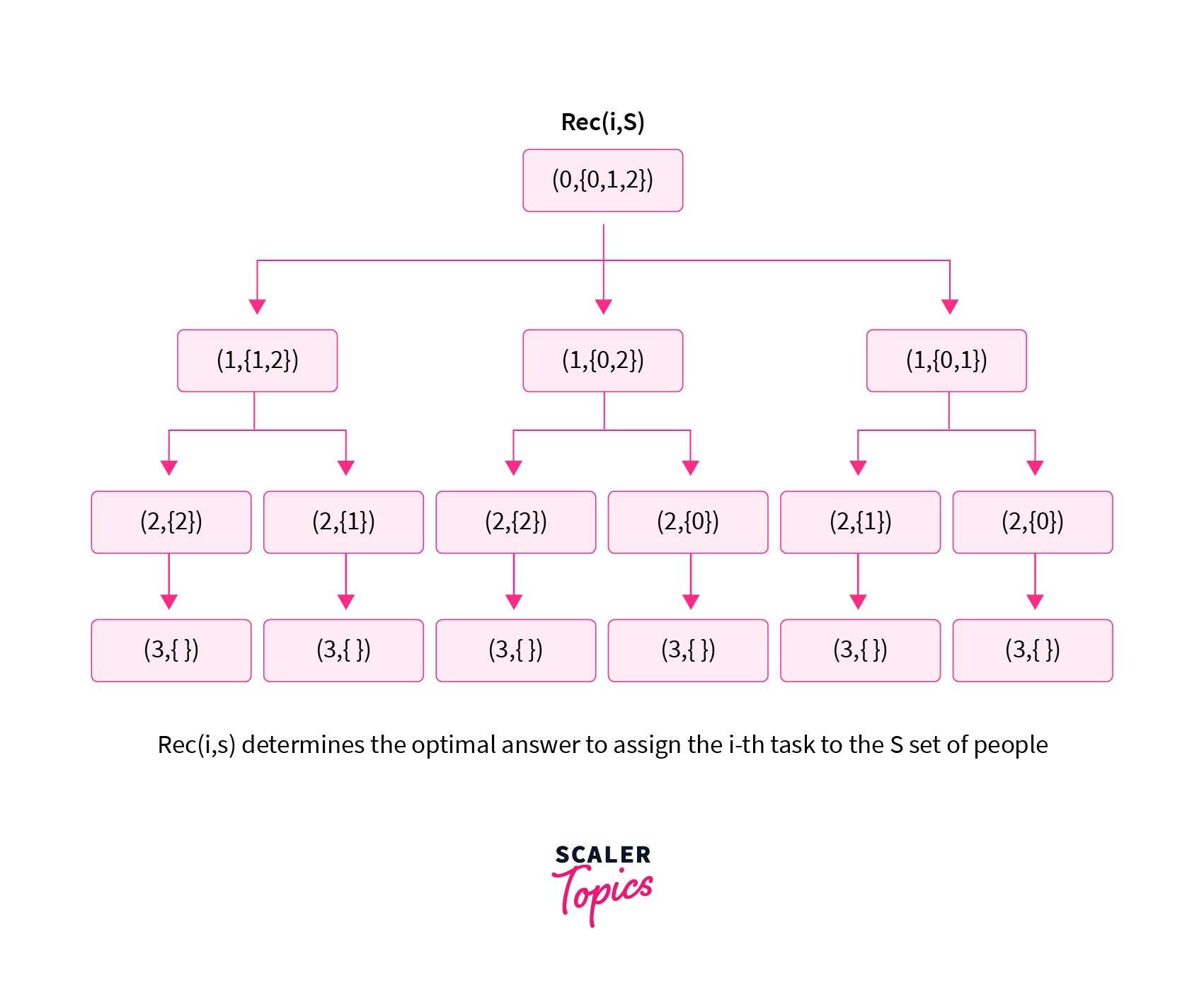
The recursion tree shown above shows the recursion to generate all the possible ways of assigning 3 tasks to 3 people. We can then select the optimal answer among them.

Now we need a way by which we can pass the set of available people in the recursion. But we have already seen how we can represent a set using bit masking in the above sections. We will use the same concept in the recursion to represent the set of available people in a set.

In the given problem to represent a set of 3 people, we will need the masks from0 to $2^3-1$, i.e from 0 to 7. Let us see how we can implement bitmasking along with recursion.

Using Recursion along with Bit Masking

As discussed above we will use the masks $0$ to $2^{N-1}$ to represent a set of N people. Each bit in a mask will represent a person in the set and will determine whether that person has been already assigned a task or not. If the $i^{th$} bit in a mask is set or is equal to 1 then that means that the $i^{th}$ person has been already been assigned a task and we can’t allot more tasks to that person. As one person can be allotted only one task. We can only assign a task to a person if the bit corresponding to that person in the mask is unset or is equal to 0.

For example, the mask 0110 will tell us that the $1-th$ and the $2-th$ (0 based indexing) person has already been assigned tasks and we can’t assign more tasks to them. We can only assign the remaining tasks to the $0-th$ and the $3-th$ persons as the $0-th$ and the $3-th$ bit in the mask is unset.

Implementation of Recursion along with Bit Masking

Let us define a function Rec(i,mask) where i represents that currently, we are assigning the $i^{th}$ task, and mask determines the set of people available to us to whom we can assign the tasks.

Initially, we will pass (0,0) to the recursive function Rec(i,mask). This will mean that we are currently assigning the $0^{th}$ task and we can assign the 0-th task to every person in the set as all the bits in 0 are unset. Inside the recursion, we will assign the current task to all the available people in the set. To check if the $k^{th}$ person can be assigned a task or not we can check whether the $k^{th}$ bit in the mask is set or not.

If the $k^{th}$ person can be assigned a task we will assign the current task to the $k^{th}$ person. While assigning the task we will also set the $k^{th}$ bit in the mask to 1 and also add the cost of assigning the current job to the $k^{th}$ person. We will then make a recursive call to assign the next job to the remaining set of people.

The recursion tree for the given approach will look as follows:

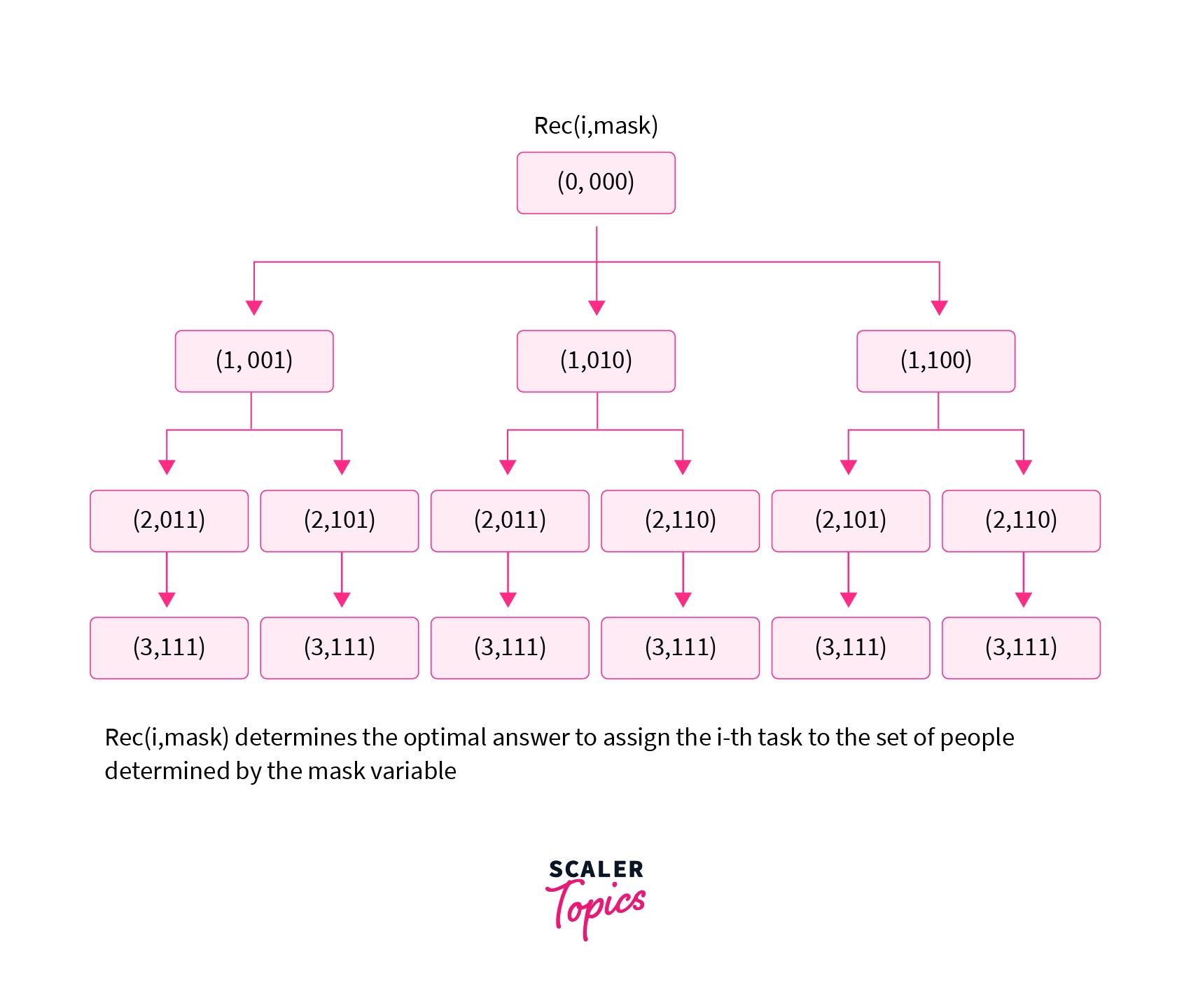
To check whether the k-th bit is set or not and how we can set a particular bit in the mask to 1 refer to the basic bitwise operations discussed above. Now let us look at the code of the algorithm discussed till now.

Base Case for the Recursion

• There is a single base case for the recursion. As we keep increasing i by 1 once we assign the $i^{th}$ task to a person. So when the value of i becomes equal to N that means that we have assigned all the N tasks to N people and there are no tasks left with us to assign. So we return 0 whenever we get i greater than or equal to `N.

C / C++ Implementation for the Recursive Approach

#include<bits/stdc++.h>
using namespace std;

int N;
int Cost[21][21];

int Maximum_Cost(int i, int mask)
{
	if (i >= N)
	{
		// base case
		return 0;
	}

	// As we need the maximum answer assign ans with the minimum
	// integer value.
	int ans = INT_MIN;

	for (int k = 0; k < N; k++)
	{
		//Check if the k-th person has been already assigned a 
		//task or not.
		if ((mask & (1 << k)) == 0)
		{
			//if k-th person has not been assigned a task,
			//add Cost[i]][k] and make the k-th bit of mask=1
			//Solve the recursion to assign i+1-th job with set
			//of people represented by the mask value.

			ans = max(ans, Cost[i][k] + Maximum_Cost(i + 1, (mask | (1 << k))));
		}
	}

	// return the optimal answer for the current state.

	return ans;
}

int main()
{

	N = 3;

	// input is same as discussed in the problem statement
	//{{2,9,7},
	// {6,4,3},
	// {1,8,5}}

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			cin >> Cost[i][j];
		}
	}

	//Print the maximum cost for assigning the tasks
	cout << "Optimal Solution for the given N and Cost Matrix is:\n";
	cout << Maximum_Cost(0, 0);

	return 0;
}

Overlapping Subproblems in the Recursion Approach

The main problem with the recursion approach is that we solve a particular subproblem several times. Due to this reason, the time complexity of the recursion approach becomes exponential. Thus the recursive approach fails to solve the problem efficiently for large inputs.

Let us understand the concept of overlapping subproblems with help of an example.

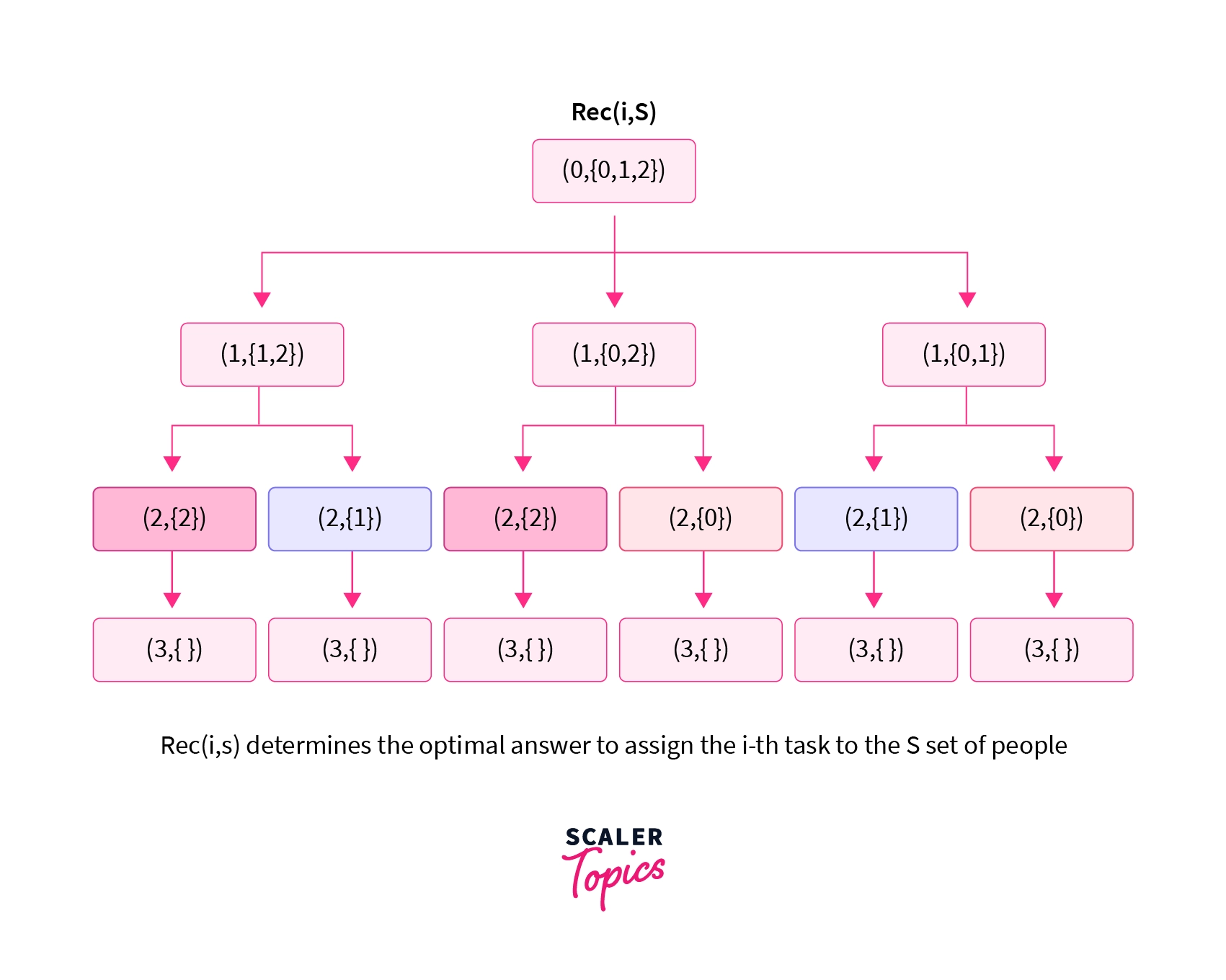
The diagram above shows the recursion tree for the input discussed above. Here we can see that the state ( 2, {2} ) appears multiple times in the recursion. These subproblems are known as overlapping subproblems as they occur multiple times in the recursion tree. We can see multiple overlapping subproblems in the recursion tree shown above.

To solve the problem of overlapping subproblems we can use Dynamic Programming. Here we make sure that one subproblem is not computed multiple times by storing the result of intermediate subproblems in an array or a vector.

Implementation of Memoization with Bit Masking

Memoization is a technique for improving the recursive algorithm. This involves making minor changes to the recursive code such that we can store the results of intermediate subproblems.

To know more about memoization and the intuitive logic behind memoization refer to the article 0-1 Knapsack Problem before moving further in this article. In this section, we will discuss how we can implement memoization for the recursion discussed above.

Let us declare a 2-Dimensional Array DP[ ][ ] which we will use to store the results of the intermediate subproblems. $DP[i][mask]$ will store the optimal result to assign the $i^{th}$ job to the set of people represented by the mask. We will initialize the DP array with -1 as the $Cost[i][j]$ can never be negative due to which our optimal answer can never be negative. Note that we can use any negative number.

Before making any recursion call we check if the value present in the DP array is equal to -1 or not. If the value present in the DP array for that state of the recursion is not equal to -1 that means that we have already calculated the optimal solution for that subproblem. Thus we return the value present in the DP array for that state of the recursion without making any recursive call.

If the value present in the DP array for that state is equal to -1 we make the recursive call and store the result of that subproblem in the DP array. Let us look at the implementation of the algorithm discussed above.

C / C++ Implementation for the Memoized Approach

We will use a global array DP[][] to store the intermediate results. $DP[i][mask]$ will store the optimal result to assign the $i^{th}$ task to the set of people represented by the mask. For N people we will need masks from 0 to $2^{N-1}$. Thus for N=20, we will need a DP array of size $DP[21][2^{20}]$. This is the maximum size of the DP array that can be required as N is always less than or equal to 20. We will initialize the DP array with -1

#include<bits/stdc++.h>
using namespace std;

int N;
int DP[21][1 << 20];
int Cost[21][21];

int Maximum_Cost(int i, int mask)
{
	if (i >= N)
	{
		// base case
		return 0;
	}

	//Before moving further in recursion check if answer for that
	//Sate has already been calculated

	if (DP[i][mask] != -1)
	{
		//Answer for the subproblem has already been calculated
		//return the answer present in DP[i][mask]
		return DP[i][mask];
	}

	//The answer for the state has not been calculated before.
	//Make the recursion call and store the result in the DP array.
	int ans = INT_MIN;

	for (int k = 0; k < N; k++)
	{
		//Check if the k-th person has been already assigned a
		//task or not.
		if ((mask & (1 << k)) == 0)
		{
			//if k-th person has not been assigned a task,
			//add Cost[i]][k] and make the k-th bit of mask=1
			//Solve the recursion to assign i+1-th job with set
			//of people represented by the mask value.

			ans = max(ans, Cost[i][k] + Maximum_Cost(i + 1, (mask | (1 << k))));
		}
	}

	// Store the result of the subproblem in the DP array.

	return DP[i][mask] = ans;
}

int main()
{

	N = 3;

	// input is same as discussed in the problem statement
	//{{2,9,7},
	// {6,4,3},
	// {1,8,5}}

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			cin >> Cost[i][j];
		}
	}

	//Initialize the DP array with -1
	memset(DP, -1, sizeof(DP));

	//Print the maximum cost for assigning the tasks
	cout << "Optimal Solution for the given N and Cost Matrix is:\n";
	cout << Maximum_Cost(0, 0);

	return 0;
}

Space Complexity

To store all the states of the recursion we are using a two-dimensional DP array of size $N\ast 2^N$. This is because for a set of size N there can maximum of $2^N$ subsets. Thus the space complexity for the given approach is $O(N\ast 2^N)$.

Time Complexity

After we have memoized the recursion using dynamic programming we are calculating a particular subproblem only once. As there can be a maximum of $N2^N$statessowewillcalculatealmost$N2^N$ states in the recursion. But for every state, we are running a loop from 0 to N-1 inside the recursion to assign a task to each person which takes an O(N) time complexity. Thus the overall time complexity for the algorithm discussed above is $O(N * (N2^N) )$whichisequalto$O(N^22^N)$.

Supercharge Your Coding Skills! Enroll Now in Scaler Academy’s DSA Course and Master Algorithmic Excellence.

Conclusion

• Bitmasking is the act of applying a mask over a value to keep, change or modify a piece of given information.
• Bitmasking can be used to solve problems where we need to deal with generating subsets of a set. However, as the bitmasking approaches involve an exponential time complexity we should be careful of the constraints given in the problem.
• In the bitmasking problems that involve overlapping subproblems, dynamic programming can be used to prevent computing a particular subproblem multiple times.