Combinatorics in Data Structure

Combinatorics is a branch of mathematics concentrating on counting, arrangement, and combination of elements within sets to satisfy specific criteria. It delves into the principles and methods used to solve problems related to permutations, combinations, graph theory, etc.

Essential to fields such as computer science, cryptography, and statistics, combinatorics plays a pivotal role in understanding complex problems by simplifying them into manageable numerical values. Its applications range from solving puzzles to optimizing complex systems, showcasing its versatility and importance in theoretical and applied mathematics.

Features of combinatorics

Combinatorics is distinguished by several key features that make it a unique and essential area of mathematics:

1. Permutations and Combinations: Combinatorics includes the study of permutations (arrangements of objects where order matters) and combinations (selections of objects where order does not matter). This aspect is fundamental in calculating probabilities and understanding various arrangements within a finite set.

2. Graph Theory: A significant part of combinatorics, graph theory explores the relationships between objects. It involves the study of graphs (networks of nodes connected by edges) and is crucial in computer science for algorithms, networking, and solving connectivity problems.

3. Enumerative Combinatorics: This area focuses on counting the number of ways specific structures can be built according to given rules, often involving sophisticated techniques for dealing with large, complex sets.

4. Algebraic Combinatorics: This branch links combinatorics with algebra by studying combinatorial structures and their algebraic properties. It involves using group theory, matrix theory, and other algebraic tools to solve combinatorial problems.

5. Combinatorial Design Theory: This field deals with the arrangement of elements within sets to meet specific criteria, often used in experimental design, error-correcting codes, and the theory of finite geometries. It emphasizes the creation of optimal configurations, ensuring balanced and systematic coverage of all variables.

Combinatorics Formulas

Combinatorics is rich with formulas that help solve many problems involving counting, arrangements, and selections. Here are some fundamental combinatorics formulas:

1. Factorial (n!): The product of all positive integers up to (n), used in permutations. $n! = n \times (n-1) \times \cdots \times 2 \times 1$ For example, $5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$

2. Permutations: The number of ways to arrange (r) objects from a group of (n) unique objects is given by $P(n, r) = \frac{n!}{(n-r)!}$ This formula is used when the order of the objects matters.

3. Combinations: The number of ways to choose (r) objects from a group of (n) unique objects, where order does not matter, is given by $C(n, r) = \frac{n!}{r!(n-r)!} = \binom{n}{r}$ This is also known as the binomial coefficient.

4. Binomial Theorem: For any positive integer (n), $(x + y)^n = \sum_{k=0}^{n} \binom{n}{k} x^{n-k} y^k$ where $\binom{n}{k}$ is a binomial coefficient. This theorem provides a formula for expanding the powers of a binomial.

These formulas are the building blocks for solving more complex combinatorial problems and are widely applied in various fields, including computer science, probability theory, and optimization.

What are permutation and Combination?

Permutation and combination serve as essential principles within combinatorics, dealing with arranging and selecting objects from a set.

Permutation:

A permutation refers to the organization of items in a particular sequence. It focuses on the sequence in which objects appear, where the order matters. For example, the permutations of the set {A, B, C} include ABC, ACB, BAC, BCA, CAB, and CBA. In permutations, changing the order creates a new arrangement.

Mathematically, the permutations of (n) objects taken (r) at a time is denoted by P(n, r) and is calculated as: $P(n, r) = \frac{n!}{(n-r)!}$

Where (n!) (n factorial) is the product of all positive integers up to (n), and (r) is the number of objects to be arranged.

Combination:

Conversely, a combination refers to the selection of objects from a set where the order does not matter. It's about choosing items without regard to how they are arranged. For example, the combinations of 2 letters from the set {A, B, C} are AB, AC, and BC. AB is considered the same as BA, as the selection order is irrelevant.

The number of combinations of n objects taken r at a time is denoted by (C(n, r)) or $\binom{n}{r}$, known as the binomial coefficient, and is calculated as: $C(n, r) = \binom{n}{r} = \frac{n!}{r!(n-r)!}$

In essence, permutations are used when the problem is about arranging or ordering. In contrast, combinations are used when the problem is about selecting or choosing without regard to the order of the selected items. These concepts are widely applied in various fields, including mathematics, statistics, computer science, and daily life decision-making.

Applications Of Combinatorics

Combinatorics cover a wide range of applications.

1. Enumerative Combinatorics is widely used in counting problems, such as analyzing sequences, tree constructions, etc.

2. Other combinatorial techniques are used to study areas such as: a. Partition Theory b. Graph Theory c. Design Theory d. Finite Geometry and many more.

3. Combinatorics is also used in the field of probability theory to understand the occurrences of structures of certain features.

Pascal Triangle

While discussing the topic of combinations, we described the following notation for choosing $k$ out of $n$ items, that was, ${}^nC_k$. This $C$ is called the binomial coefficient.

As shown below, a table of binomial coefficients is popularly known as Pascal's triangle (sometimes also called Pascal-Pingala Triangle, or Pingala's Meruparastara).

This triangle shows the first 6 rows of the triangle. But how is this triangle generated? The rules are as follows:

1. Every row starts with 1 and ends with 1
2. The other in-between elements are just the sum of elements present on the right and left in the previous row.

The image below shows the flow of the calculation:

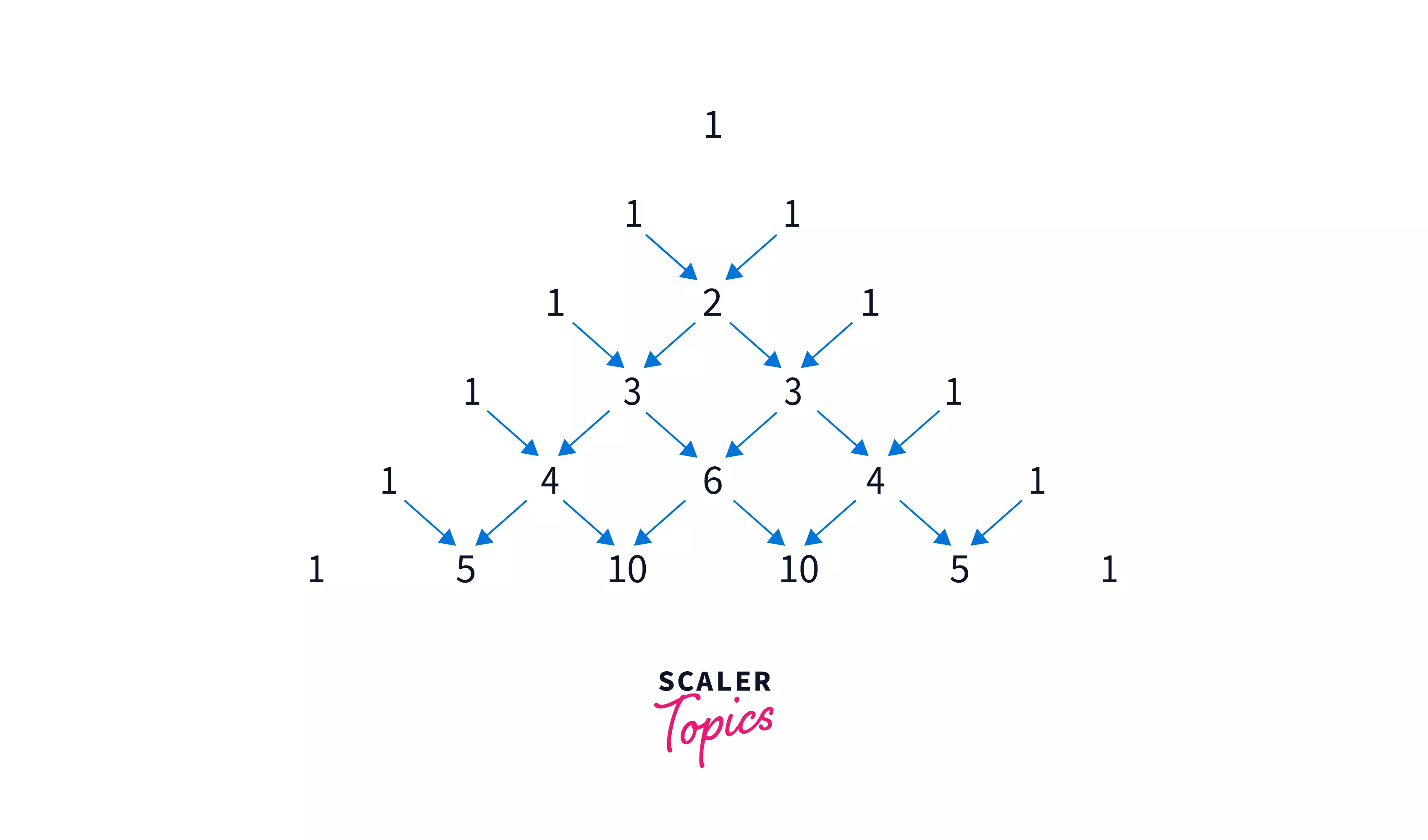
But we still need to see how this relates to binomial coefficients. It's as follows:

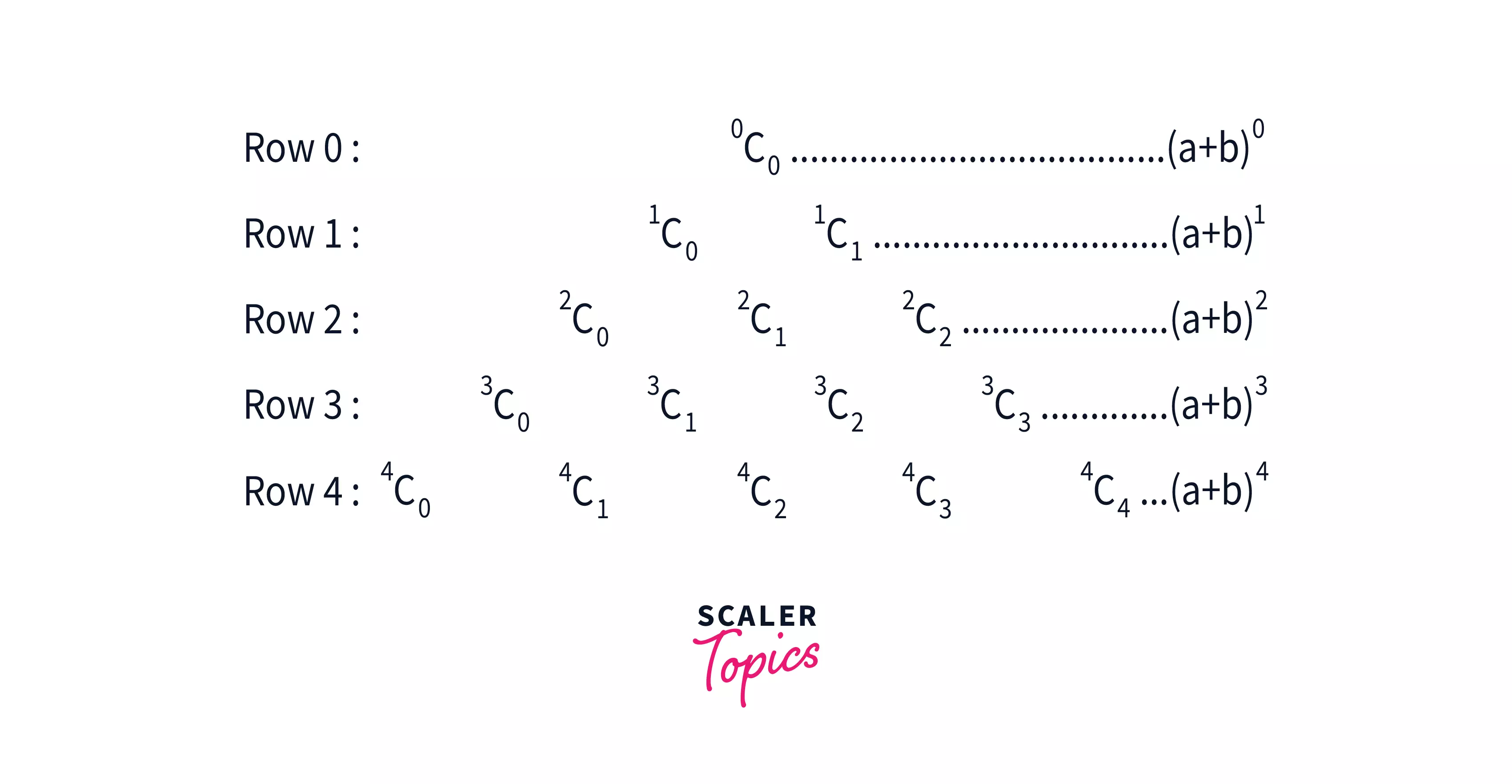
As shown above, row $n$ provides us with the coefficients of binomial terms $a^ib^j$ upon expansion of $(a+b)^n$, that is, ${}^nC_i$.

For example, on expansion of $(a+b)^3$, we get

The coefficients are 1, 3, 3, 1, which are the same as the contents of row 3.

Combinatorics Solved Examples

Combinatorics problems vary widely, but here are a couple of solved examples that illustrate the application of permutation and combination formulas to solve typical combinatorial problems:

Example 1: Permutation Problem

Problem: In a race with 10 runners, how many ways can the first, second, and third places be awarded?

Solution: We use the permutation formula Since this is a permutation problem (the order matters). We have 10 choices for the first place, 9 for the second (after the first has been chosen), and 8 for the third. Thus, the total number of different ways to award the first three places is: $P(10, 3) = \frac{10!}{(10-3)!} = \frac{10!}{7!} = 10 \times 9 \times 8 = 720$

So, there are 720 different ways to award the first three places in the race.

Example 2: Combination Problem

Problem: A committee of 4 members needs to be formed from 10 people. How many different committees can be formed?

Solution: We use the combination formula Since this is a combination problem (the order does not matter). We want to select 4 people out of 10, without regard to the order of selection: $C(10, 4) = \binom{10}{4} = \frac{10!}{4!(10-4)!} = \frac{10!}{4!6!}$

Calculating the factorials and simplifying: $\frac{10 \times 9 \times 8 \times 7}{4 \times 3 \times 2 \times 1} = 210$

So, there are 210 different ways to form a committee of 4 members from a group of 10 people.

These examples demonstrate how permutation and combination formulas are applied to solve problems involving arrangements and selections in combinatorics.