Extended Sieve

Introduction

Prime numbers are one of the most important concepts of mathematics. They find their use in a variety of applications, especially in cryptography. And if they are so important there must be a way to find prime numbers efficiently instead of performing a time-taking primality check. Hence 2200 Years ago, Eratosthenes (A Greek mathematician) came up with an approach that is vastly used in calculating prime numbers in a range which is known as the Sieve of Eratosthenes or more commonly simply "Sieve".

What is Sieve of Eratosthenes

Sieve of Eratosthenes is an algorithm that is used to find prime numbers in the range $[1,n]$ for a given $n$. The basic idea behind Sieve is to initially assume all numbers from $2$ to $n$ as prime (as it is known that $1$ is not prime) and iterate from $i=2$ to $\sqrt{n}$ and if $i$ is marked as a prime number then mark all the multiples $i$ as non-primes (composite). The algorithm is discussed in depth in our previous article Sieve of Eratosthenes, please go through it to understand it more clearly.

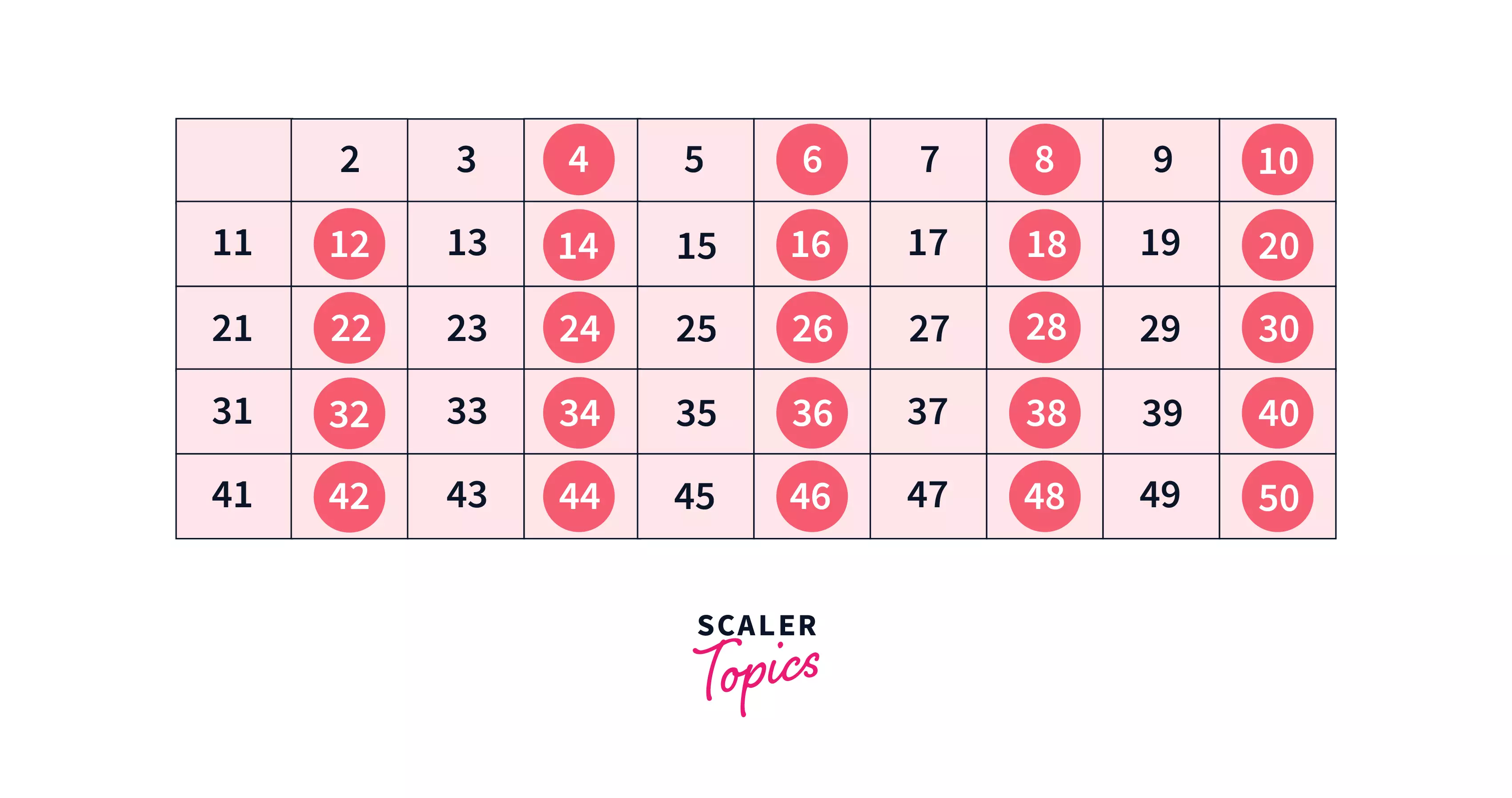
Problem with Sieve of Eratosthenes

The major and the only issue with the standard implementation of Sieve is, the extra $O(n)$ space (visited array) is needed to find all prime numbers in the range $[1,n]$. Imagine a situation, where we need to find all prime numbers in the range $[1,10^7]$ using the standard Sieve of Eratosthenes algorithm. It would not be an efficient approach as it is difficult to allocate $O(n)$ extra space when $n\geq 10^7$. If somehow we can optimize space complexity then we can solve the issue. For that, we have a modified algorithm called "Extended Sieve of Eratosthenes".

What is Extended Sieve of Eratosthenes?

The main idea behind the extended sieve is to divide the range of $[1,n]$ into many segments, and compute primes of each segment one by one. Now the question arises that how much should be the size of each segment. Generally, the size of each segment is taken around $\sqrt n$.

After which the segments will look like, $[1,\sqrt n],$ $[(\sqrt n +1), (2\times\sqrt n)],$ $...,$ and $[(n-\sqrt n), n]$.

For Example: Let's assume $n$ to be $16$ then we will not find prime numbers in the range $[1,16]$. Instead we will find primes in the segments - $[1,4],$ $[5, 8],$ $[9,12]$, and $[13,16]$ indvidually.

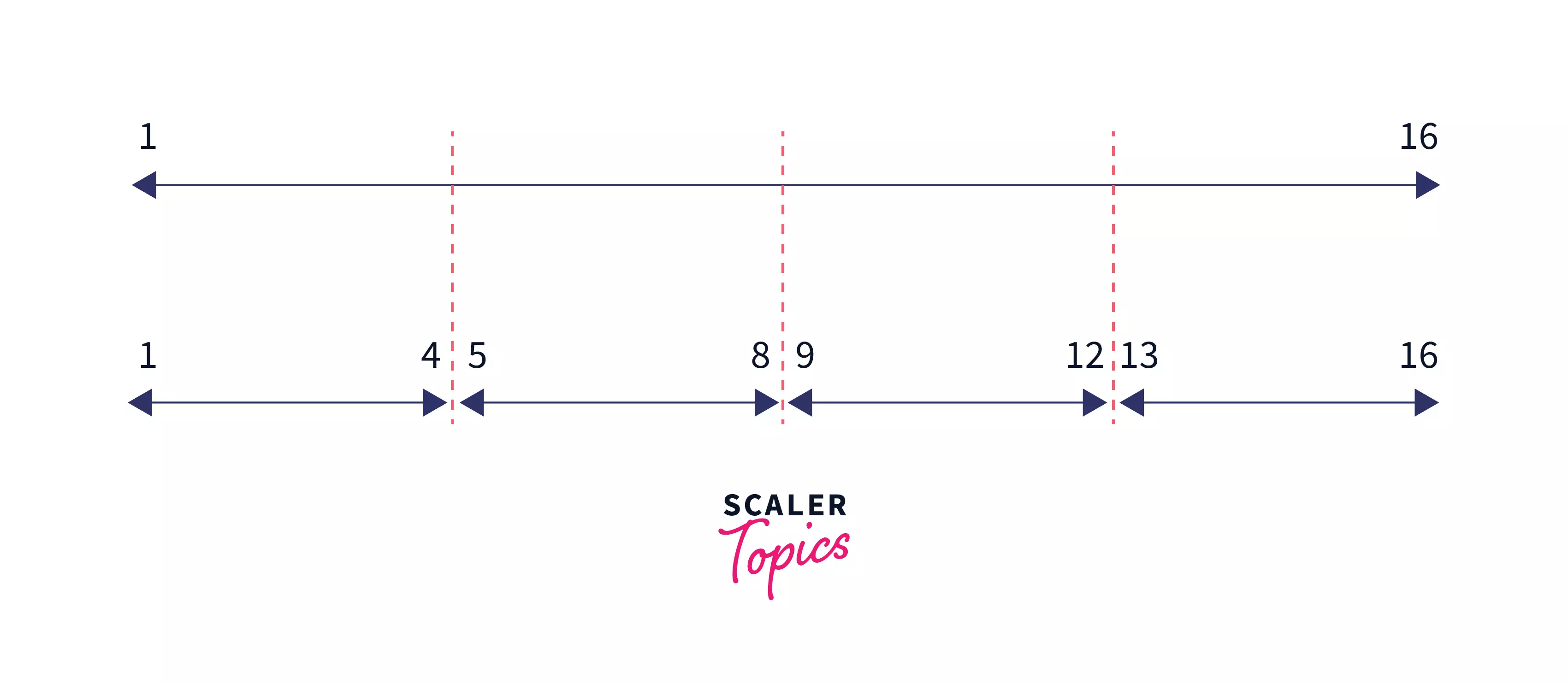
Below are the steps for implementing the extended sieve of Eratosthenes:

• Divide the range $[1,n]$ into segments of size at most $\sqrt n$.
• Use the standard sieve to find prime numbers up to $\sqrt n$ and store them in an array/list prime.
• Do the following for each segment $[low, high]$
  • Create a boolean visited array of size $high-low+1$ and mark all its entries to be true.
  • Iterate through all the prime numbers stored in the list prime and mark all its multiples as false that lies in the range $[low, high]$.

We are doing the third step because we want to find the prime numbers belonging to a range $[\sqrt{n}+1, 2\times\sqrt n],$ $[(2\times\sqrt{n})+1, 3\times\sqrt n]$ and so on. By performing the third step it can be done easily.

Example of Extended Sieve

Let's say we want to find all prime numbers less than or equal to 50 using the extended Sieve algorithm as discussed above.

• Firstly we will divide the range of $[1,50]$ into some segments of size $\lfloor \sqrt{n}+1\rfloor$. We know that $\sqrt{50}=7.07$ and hence $\lfloor \sqrt{n}+1\rfloor=8$. So the segments will be like -

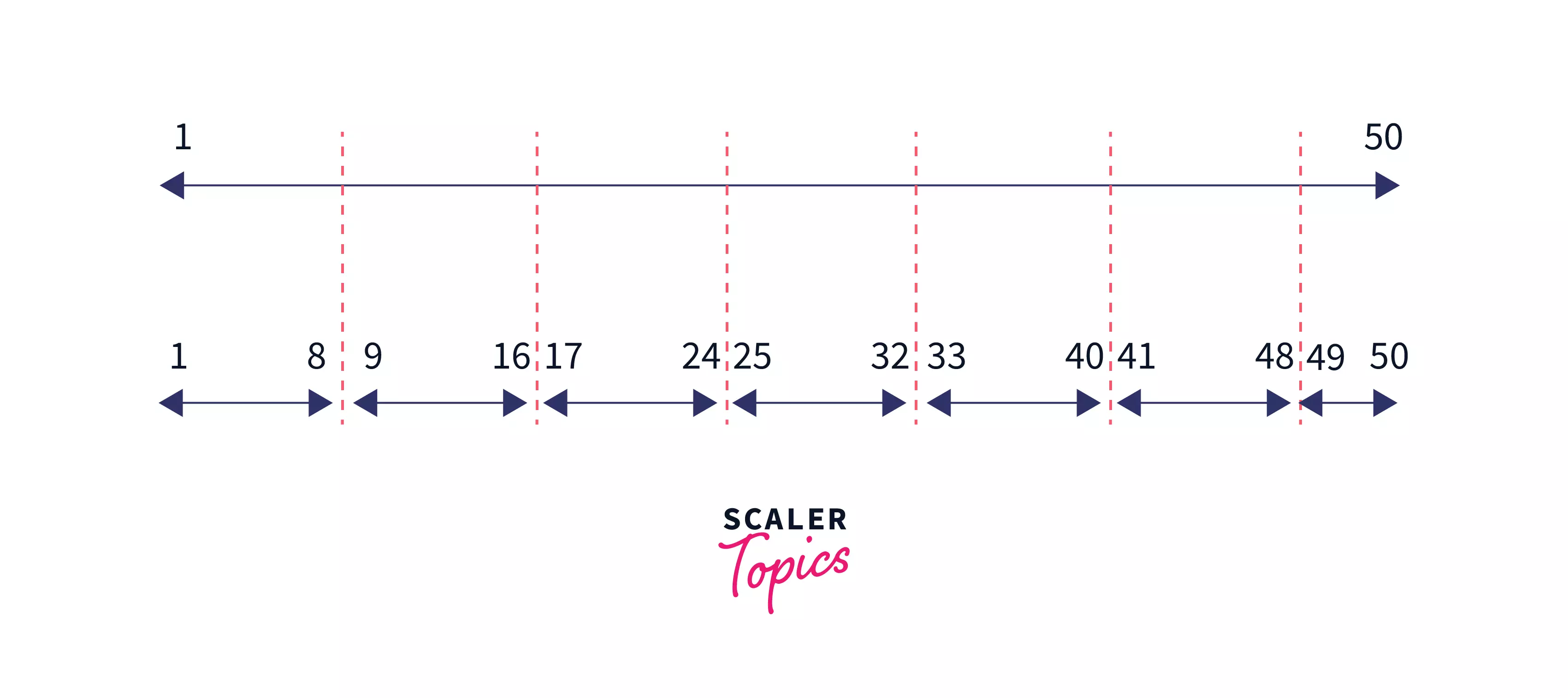
• Now using the Standard sieve we will find and print all prime numbers in the range $[1,8]$ and store them in list prime. After performing we will have - prime=[2,3,5,7]

• For segment $[9,16]$, we will make a boolean array visited and mark all elements as true (For easier representation we consider strikethrough numbers as false otherwise true). Now we will check for multiples of all numbers in prime (say $x$) that lie in the range $[9,16]$ and mark them false. After which boolean array will look like - visited = 9, 10, 11, 12, 13, 14, 15, 16. Now we will print and add all the un-marked numbers in prime, because they are not divisible by any number present in prime and hence they are prime numbers.

• Similarly for the segment $[17, 24]$, we will have - visited= 17, 18, 19, 20, 21, 22, 23, 24. Again, due to the same reason we will print and add 17, 19, and 23 in primes.

• Perform the same procedure for all the other segments, at last, we will have the following elements printed on the user console and in the list. prime= 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47

Implementation of Extended Sieve

Let's say we want to find the prime numbers in the range $[1,n]$ using the extended sieve.

• The first step would be finding the size of segments in which we divide the problem. In general practice, $size$ is taken as $\lfloor \sqrt{n}\rfloor+1$.
• Then we would declare a list (say prime) which would store all the prime numbers of the range $[1,size]$.
• Now, we will run the classical sieve algorithm for the range $[1, size]$.
• Then we will define our next interval using $low$ as $size+1$ and $high$ as $2\times size$.
• Mark all the multiples of numbers in prime belonging to the range $[low, high]$ as non-primes(composite).
• Add $size$ to low and high and repeat the above steps till $low<n$.

Pseudocode:

C/C++ implementation of Extended Sieve

Java implementation of Extended Sieve

Output:

Complexity Analysis

• Time Complexity - Here we are using the standard sieve of Eratosthenes multiple times but for a smaller range of numbers. It does not affect the time complexity as we are dividing the range into some number of segments and solving each segment individually. Hence the time complexity is the same as of standard sieve $i.e.$ $O(n\times\log{(\log n)})$. For the proof of time complexity please refer to Sieve of Eratosthenes.

• Space Complexity - We are using an auxiliary boolean array visited of length ($size+1$), where $size=\sqrt{n}$. Hence the space complexity is $O(\sqrt{n})$.