Fenwick Tree | Binary Indexed Trees

The Binary Indexed Tree, also known as the Fenwick tree, provides an efficient way to calculate prefix sums of a series of numbers, especially in scenarios where the values are mutable. Unlike prefix sum arrays, which excel in answering prefix sum queries but struggle with frequent updates, Fenwick trees offer a balance between efficient query answering and mutable value updates.

By maintaining cumulative frequencies of array elements at each node, Fenwick trees enable prefix sum calculations in logarithmic time complexity.

Utilizing the concept that any integer will be expressed as the sum of powers of 2, Fenwick trees store the sum of a specific range of elements at an index in the auxiliary array, facilitating quick prefix sum computations with minimal space overhead.

For Example:

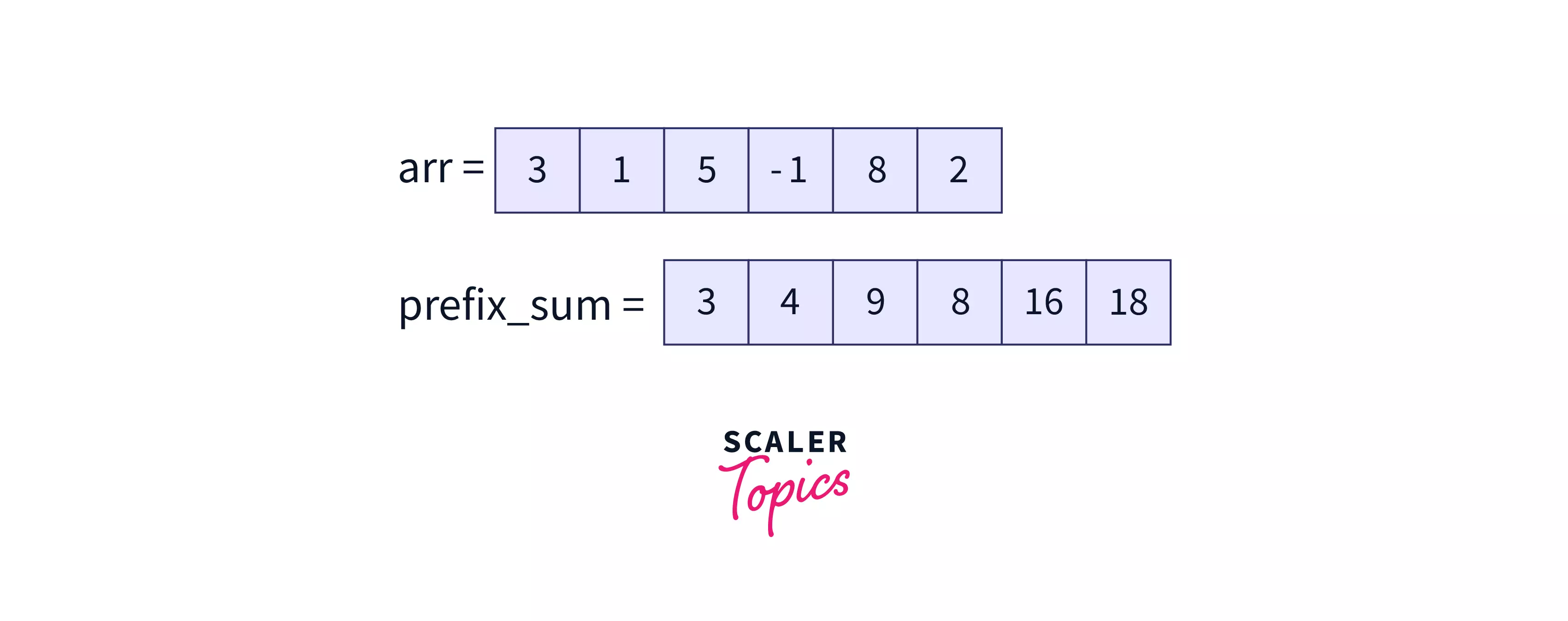
Representation of Fenwick Tree

The BIT (Binary Indexed Tree) is represented as an array (say $bit$). Where each index of $bit$ stores the sum of a range of elements of the original array (say $a$).

Let $i$ be an index of the array $bit$, then $bit[i]$ will contain the sum of elements KaTeX parse error: $ within math mode where $x$ is the position of the least significant set-bit in the binary representation of $i$.

Let us understand by an Example: Let's say we want to know the range of which sum is stored in $bit[12]$, we know that binary representation of $12$ is $1100$, we can see that the position of least significant set-bit from right, $x$ is $3$.

That means $bit[12]$ will contain the sum of the range $(13-2^{3-1}+1) \rightarrow 12$ $i.e.$ $9 \rightarrow 12$.

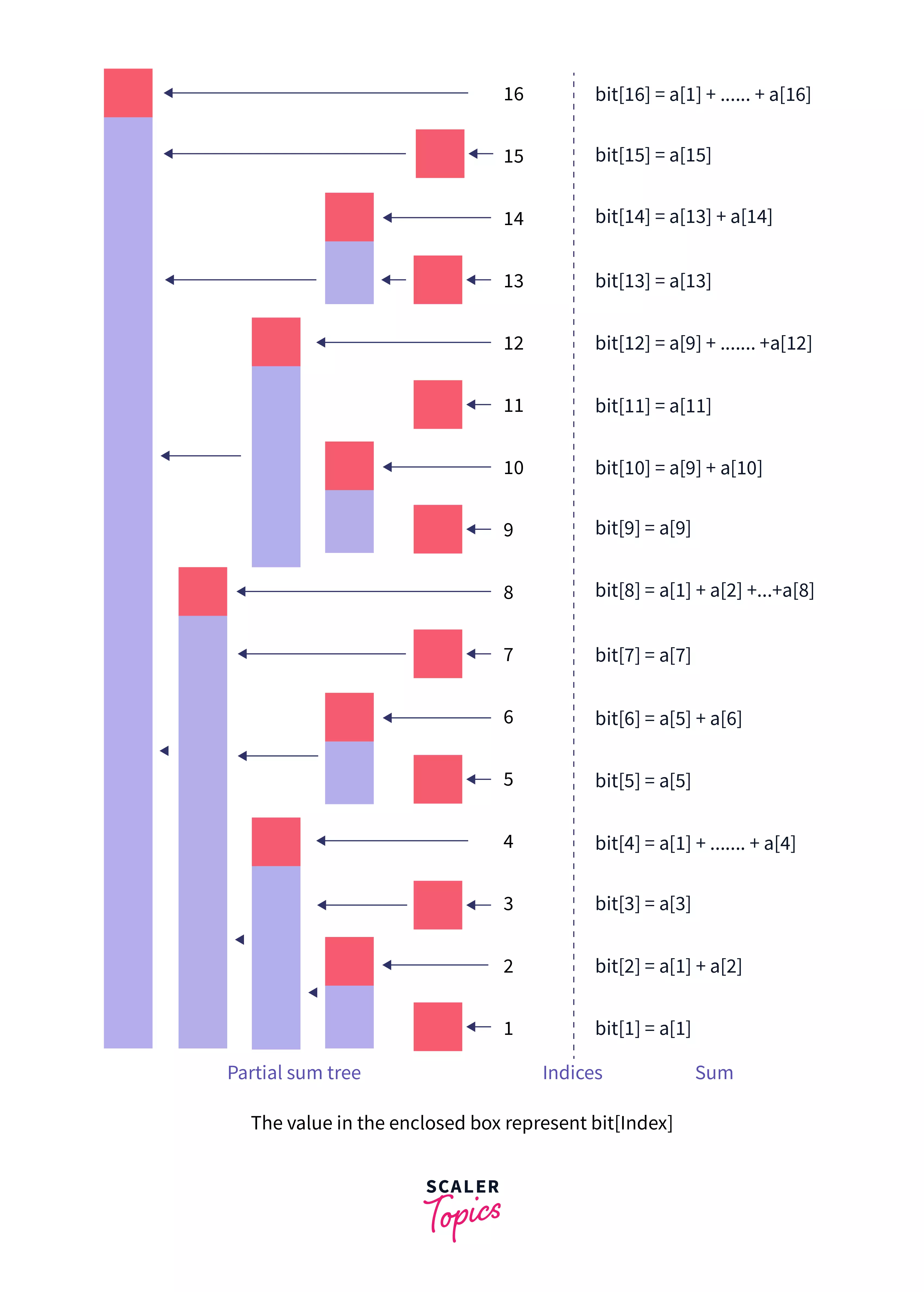
The above image represents the range of elements for which the sum is stored for any index i in the bit array of size 16.

For Example: index 12 in bit holds the sum of the values of the range $[9\rightarrow 12]$ present in a and index 8 in bit holds the sum of the values of the range $[1\rightarrow 8]$ in a. So to find the prefix_sum[12] we can simply find $bit[12]+bit[8]$ instead of calculating sum one by one.

Construction of Fenwick Tree

Let's say we have been given an array $a$, of size $n$. So we will create another array of size $n+1$(say $bit$) all of its entries will be initialized with 0. Then we will use the update function for each index of array $a$. Its pseudocode will be like -

For Example: Let $a=\{4,2,1,5,6,3,9,7,2,3\}$ Then $bit$ array will correspond to - $\{4,6,1,12,6,9,9 ,37,2,5 \}$ where $bit[i]$ represents sum of range $(i-2^{x-1}+1) \rightarrow i$

Operations of Fenwick Tree

The two main operations supported by Fewick tree are -

• getSum(x) - This operation returns the sum of first $x$ elements of the array $i.e.$ $a[0]+a[1]+...+a[x]$.
• update(x,val) - This operation updates the value of $a$ at index $x$ $i.e.$ $a[x]=val$

We can also find the sum of any arbitrary range $[left,right]$ using the below-given function which uses getSum(x) to find the same.

getSumRange(left, right): This operation returns the sum of array elements within a range $i.e.$ $a[left]+a[left+1]+...+a[right]$. It can be easily calculated using _getSum(x)_ operation by returning getSum(right+1)-getSum(left)

How does Binary Indexed Tree work?

The core idea revolves around leveraging the property that any positive integer can be expressed into a sum of powers of 2.

For instance, take the number 15, which can be expressed as 8 + 4 + 2 + 1. Within the Binary Indexed Tree (BIT), each node aggregates the sum of a distinct range of elements. The range of elements represented by each node in the Binary Indexed Tree (BIT) is determined by the position of the least significant set bit in its binary index. Consider an example where we need to calculate the sum of the first 15 elements. To achieve this, we sum the last 8 elements (from 8 to 15) along with the sum of the preceding 4 elements (from 4 to 7) and the initial 2 elements (from 2 to 3). As the number of set bits in a number's binary representation is O(Logn), both getSum() and update() operations traverse at most O(Logn) nodes. Building the Binary Indexed Tree (BIT) requires O(nLogn) time complexity since it invokes the update() function for each of the n elements.

getSum(x) operation:

getSum(x) operation returns sum of array elements from $0^{th}$ index to $x^{th}$ index $i.e.$ $a[0]+a[1]+...+a[x]$. Steps invloved to calculate it are -

• Initialize answer, ans with 0.
• Increase x by 1 (To maintain 1-based indexing).
• While x is greater than 0
  • $ans+=bit[x]$
  • $x-=(x\&(-x))$
• Move to the parent of the BITree[index] by eliminating the rightmost set bit from the current index. i.e. $x-=(x\&(-x))$.
• Return ans

update(x, val) operation

update(x, val) operation updates the value of array $a$ at index $x$ to $val$. After updating, we also need to update $bit$ array at those indices which get impacted by the element at index $x$. , Steps involved in that are -

• Find the change happening at the index x, $\delta val=val-a[x]$.
• Update the value at index x $i.e.$ $a[x]=val$.
• While $x\leq n$
  • $bit[x]+=\delta val$
  • $x+=(x\&(-x))$
• Move to the next element of BITree[index] by incrementing the rightmost set bit of the current index. i.e. $x+=(x\&(-x))$.

Code Implementation

To implement the Fenwick tree (BIT) we will have the following global variables to maintain simplicity in the code.

• n- It denotes the size of the array on which we want to perform certain operations which are discussed in the previous sections.
• bit- It is the actual binary indexed tree that is represented in array format. Its size will be n+1 to maintain 1-based indexing.

The functions which are needed to implement functionalities of the binary indexed trees are :

• FindSum- It takes one argument (say ind) and we need to return the sum of values of the given array (say a) in the range [0, ind].
• SumOfRange- It takes two arguments (say left and right) and we will return the sum of values of a in the range [left, right]
• Update- It takes two arguments (sat ind and val) and we need to change the value of a at index ind to val and correspondingly we also need to update the bit.

C++:

Java:

Python:

Output: Sum of range 2-6 is 24. Sum of range 5-9 is 33.

Complexity Analysis of Fenwick Tree

• Time Complexity:
  • Construction: O(n * log n)
  • Query: O(log n)
  • Update: O(log n)

This is because the number of nodes visited is proportional to the number of set bits in the binary representation of the index.

• Space Complexity:
  • O(n)

Applications of Fenwick Tree

Fenwick Tree is mainly used to optimize the process of finding the prefix sum of the arrays such that we can have the prefix sum of an array index in logarithmic time complexity. However, there are some popular questions that can be efficiently solved using Fenwick trees:

• Mutable Range Sum Queries: Q queries can be answered in $O(Q\times \log{n})$ time which is way better than $O(Q\times N)$ run-time of brute force approach.
• Count Inversions in an Array: The number of inversions can easily be found in $O(n\times \log{n})$ time even without sorting the array.
• Count smaller numbers after self: Many practical uses can be seen in the real world which can be computed efficiently using BIT.