Floyd Warshall Algorithm

Overview
Floyd Warshall algorithm is used to find the shortest path between all vertices in the weighted graph. This algorithm works with both directed and undirected graphs but it does not work along with the graph with negative cycles.
Takeaways
-
Floyd Warshall's Algorithm is used for solving all pair shortest path problems.
-
Complexity of Floyd Warshall's Algorithm
- Time complexity - O()
- Space complexity - O(n)
Introduction of Floyd Warshall Algorithm
If you’re looking for an algorithm for scenarios like finding the shortest distance between every pair of stations in a subway, then all hail the mighty polynomial-time Floyd-Warshall algorithm!
In other words, the Floyd-Warshall algorithm is an ideal choice for finding the length of the shortest path across every pair of nodes in a graph data structure.
Albeit, the graph shouldn’t contain any negative weight cycles. 🤞🏻
You see, the Floyd-Warshall algorithm does support negative weight edges in a directed graph so long the weighted sum of such edges forming a cycle isn’t negative.
And that’s what I mean by a negative weight cycle!
Think about it, if there exists such a negative cycle, we can always just keep traversing this cycle over and over while making the length of the path smaller and smaller. Keep doing it, and the length eventually approaches negative infinity which is absurd!
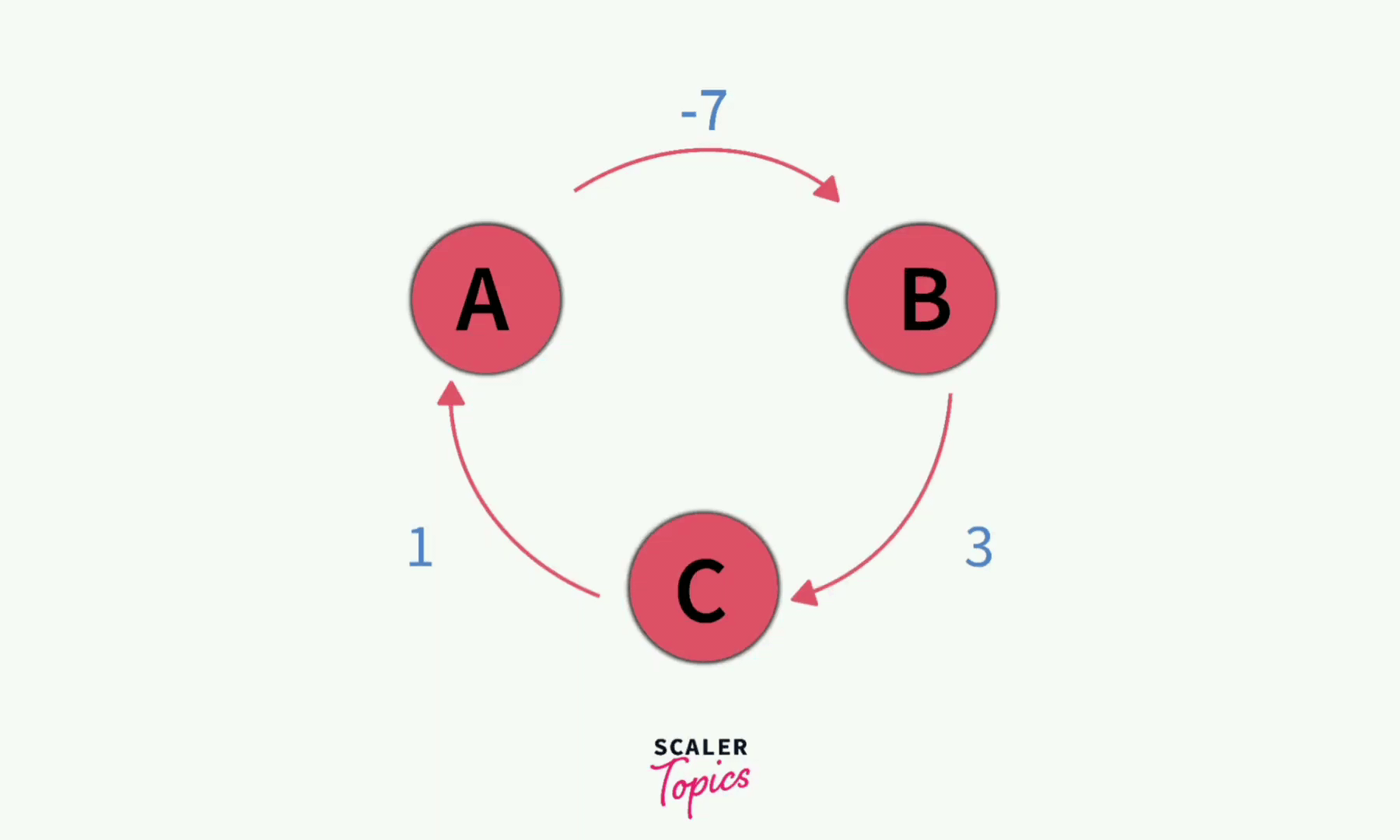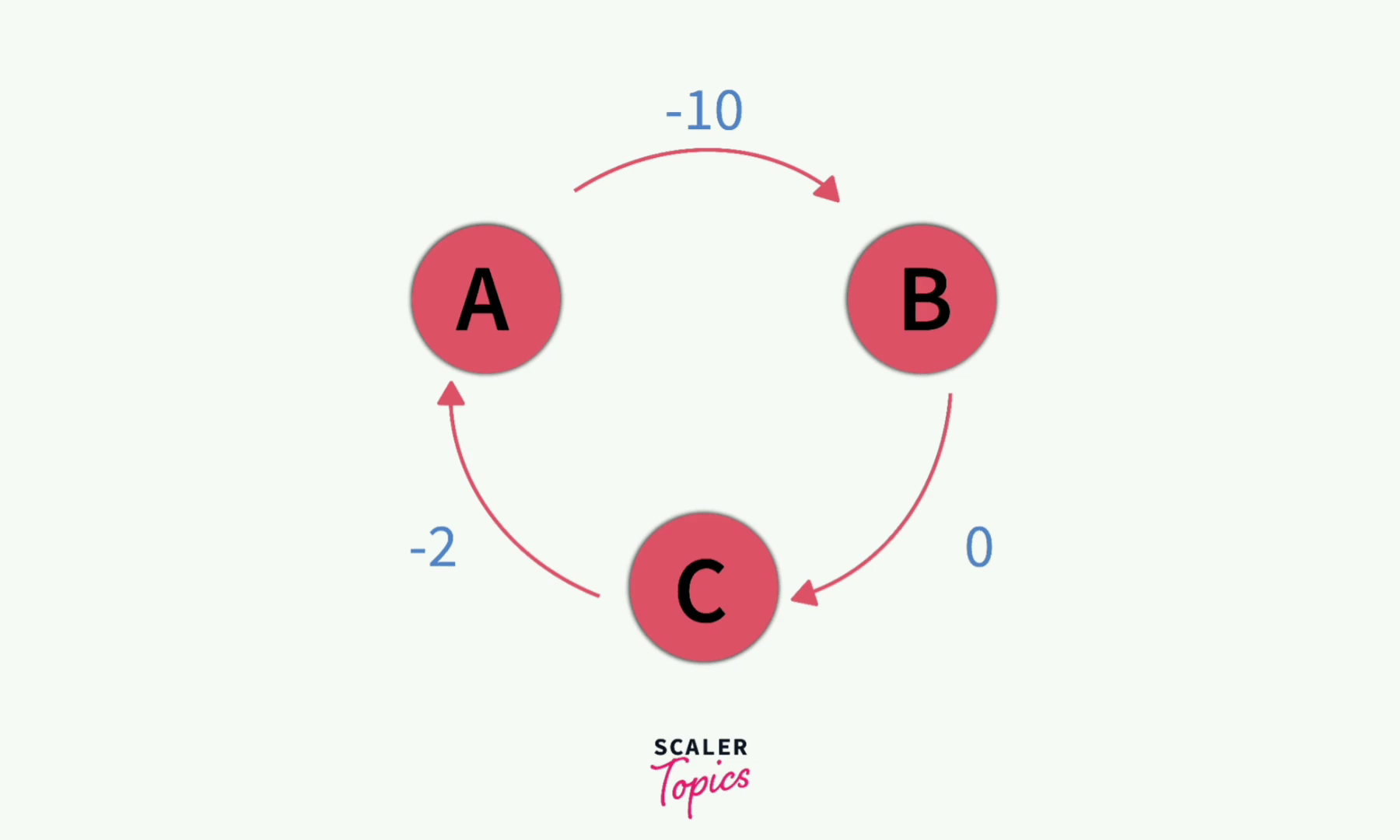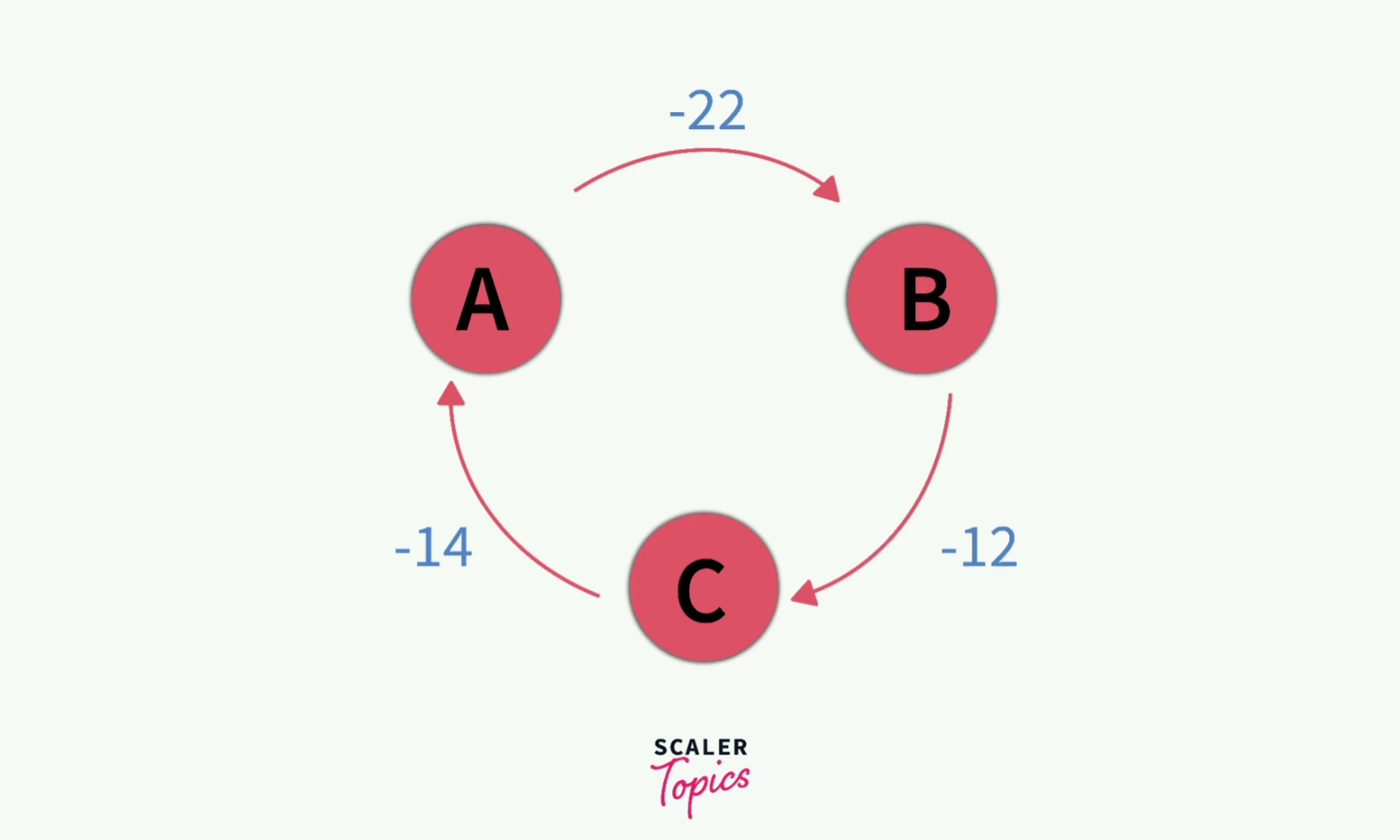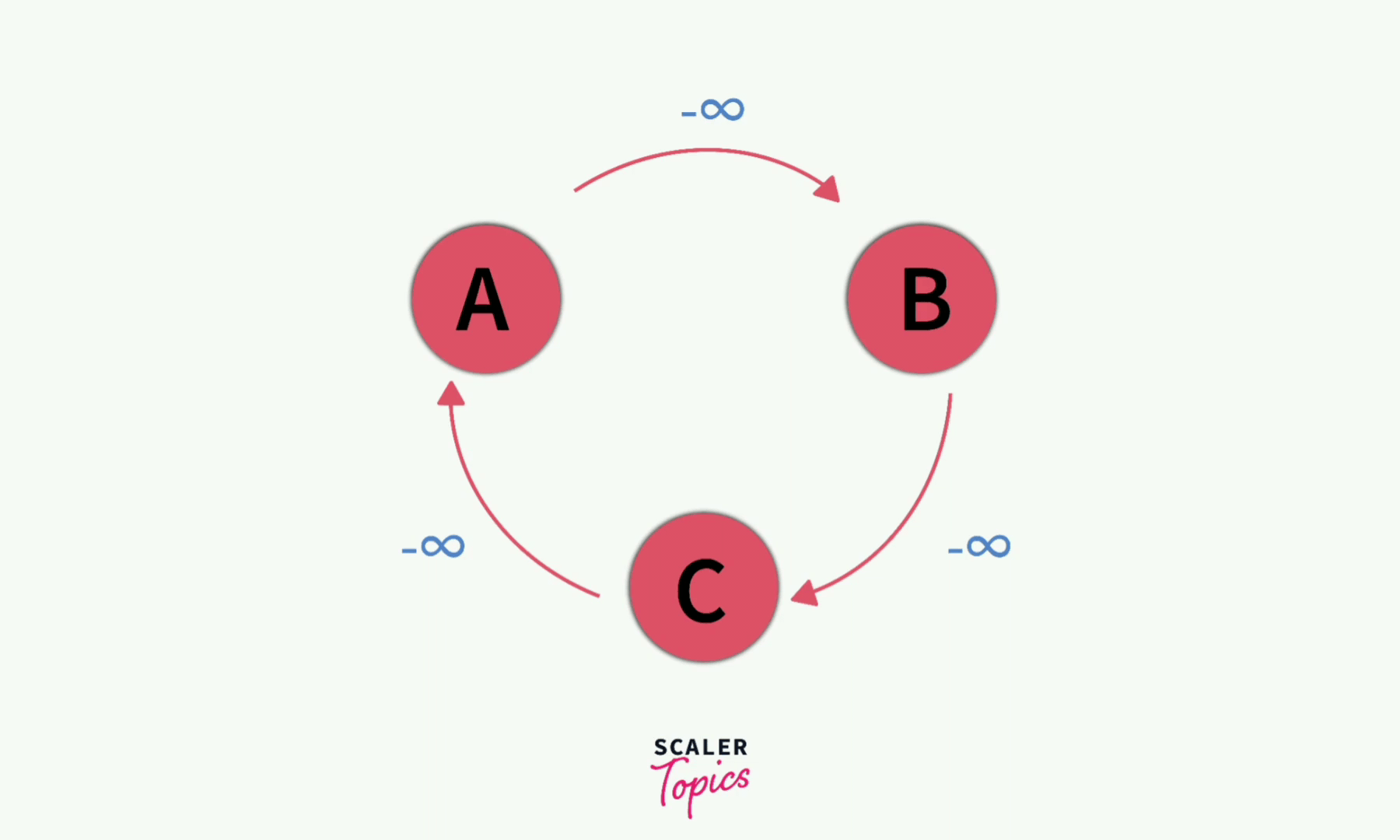
Also if we observe, the algorithm can’t support negative weight edges in an undirected graph at all. Such an edge forms a negative cycle in and of itself since we can traverse back and forth along that edge infinitely as it’s an undirected graph.
Well, you might argue why bother learning another algorithm when we can solve the same stuff by extending the Bellman-Ford or Dijkstra’s shortest path algorithm on every node in the graph.
Technically you can, but we don't use Dijkstra/Bellman-ford...
Because of time complexity! ⏰
Will discuss more on that later…
Now that we have a fair share of understanding as to what is and why we need the Floyd-Warshall algorithm, let’s peek behind the curtains and see how it works!
How Does The Floyd-Warshall Algorithm Work?
Let’s understand the flow by considering the following graph:
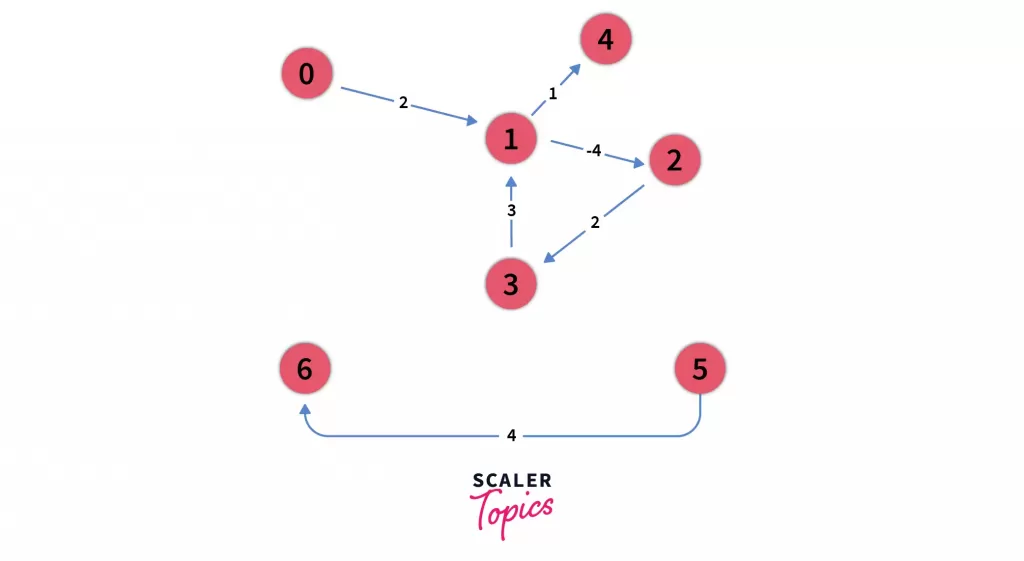
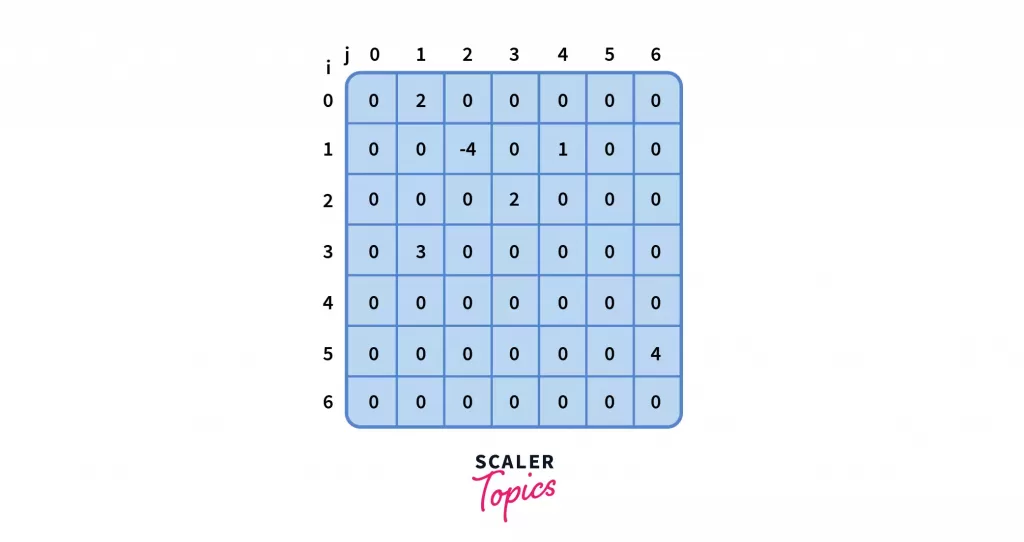
- This graph can also be represented by the following adjacency matrix A of size nxn where the row and the column are indexed as i and j respectively.
In our case, n = 7 and i, j corresponds to nodes belonging to the graph.
- The next step is to create a corresponding distance matrix D having the same dimension as A which satisfies the following conditions:
| D[i][j] = A[i][j] | if A[i][j] ≄ 0 | when an weighted edge A[i][j] is present between nodes i & j |
|---|---|---|
| D[i][j] = ∞ | if A[i][j] = 0 and i ≄ j | when no edge is present between two different nodes i & j |
| D[i][j] = 0 | if i = j, | when nodes i and j are same |
where D[i][j] refers to the distance from node i to node j.
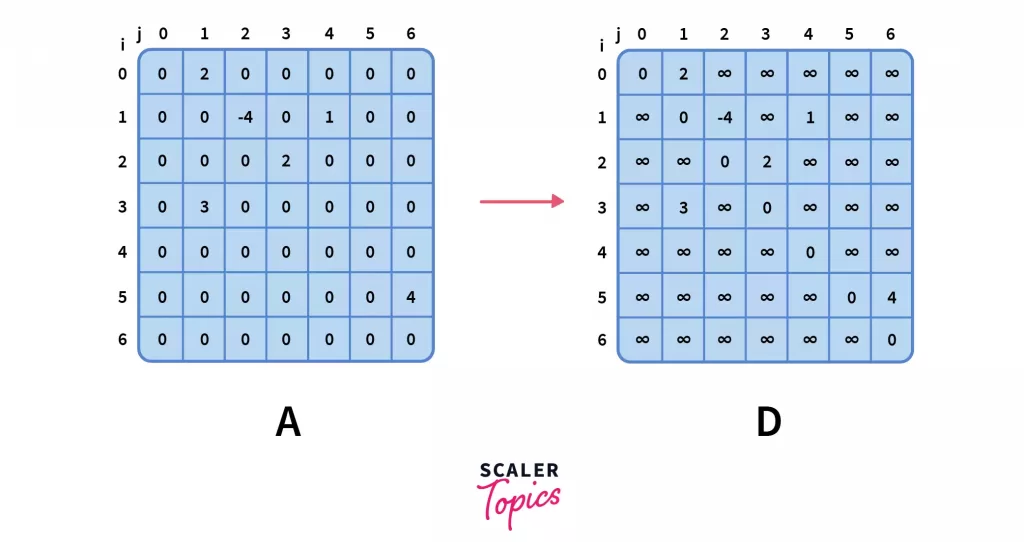
This distance matrix will eventually serve as a constant time lookup for the shortest path across every pair of nodes once the Floyd-Warshall algorithm runs its course.
- Notice how D[2][1] equals infinity at this moment however if you look at the original graph closely, you can see there’s a path via node 3:
This implies that 5 is the shortest distance from node 2 to node 1 and not infinity.
Now ask yourself, can this hold for other pairs of nodes as well? 🤔
This little insight is what led to the development of the Floyd-Warshall algorithm!
- The crux of the algorithm is to pick a node, say k and use it as an intermediate node for every other pair of nodes, i and j.
Now, picking an intermediate node can increase or decrease the overall distance, so make sure you always pick the minimum distance as shown below:
- Let’s walk through the process by picking node 0 as the intermediate node.
Scroll up and look at the graph again, you will see no path exists via node 0. You can also confirm the same from the distance matrix itself since D[i][0] = ∞ for every i.
So, we can conclude that the distance matrix remains the same when k = 0.
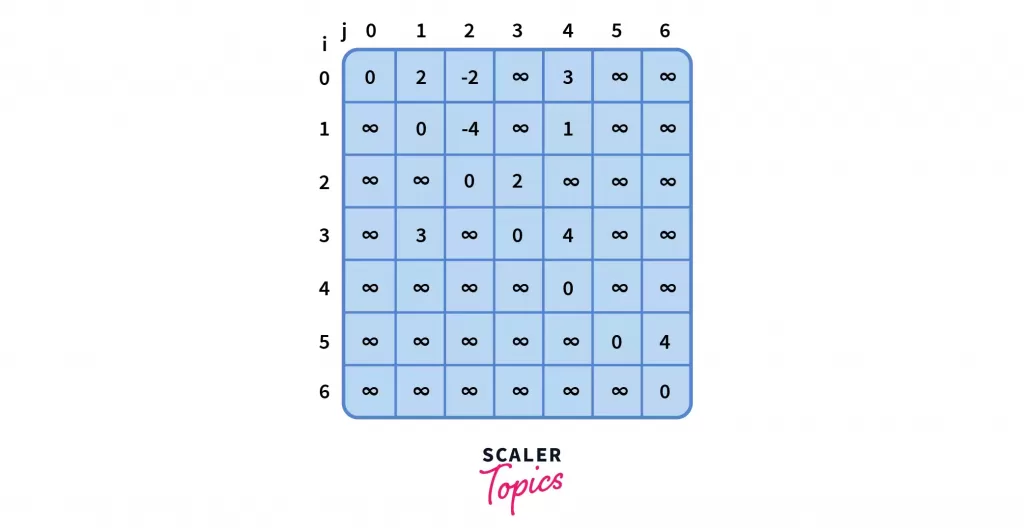
- Moving on, we pick node 1 as the next intermediate node. But this time the distance matrix does get an update like so,
Since, above mentioned cells had infinity as their previous value, hence any finite number would be a minimum.
Note that we actually checked for all pairs of i and jsuch asD[4][2] = D[4][1] + D[1][2] = ∞ + (-4) = ∞` which implied no updation. It is only after checking all possible pairs did we conclude that those three above mentioned cells got an update.
-
Let’s repeat the procedure for k = 2,
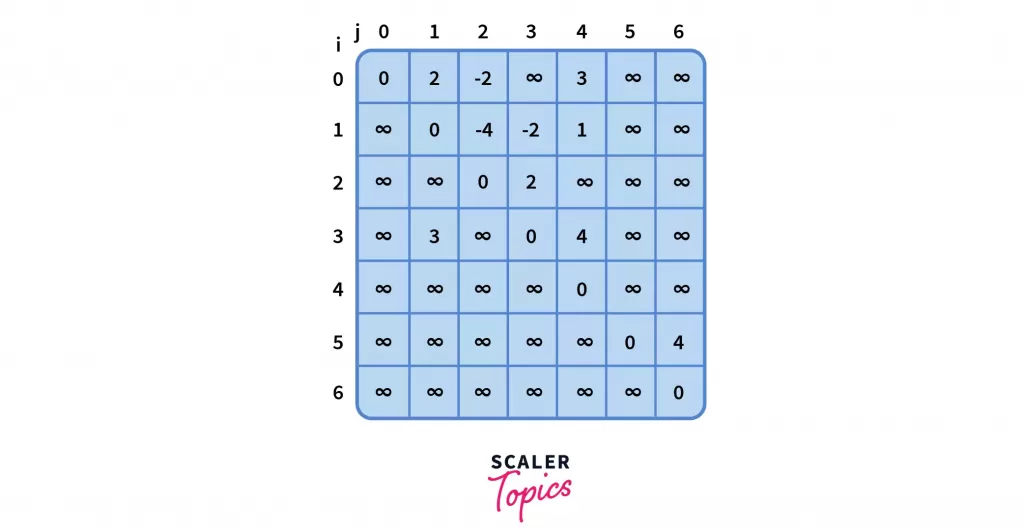
-
Similarly, for k = 3,

-
Lastly, for nodes 4, 5 and 6, the distance matrix doesn’t get updated due to the reasoning we had for k = 0. Thus, the final distance matrix D, as it stands,
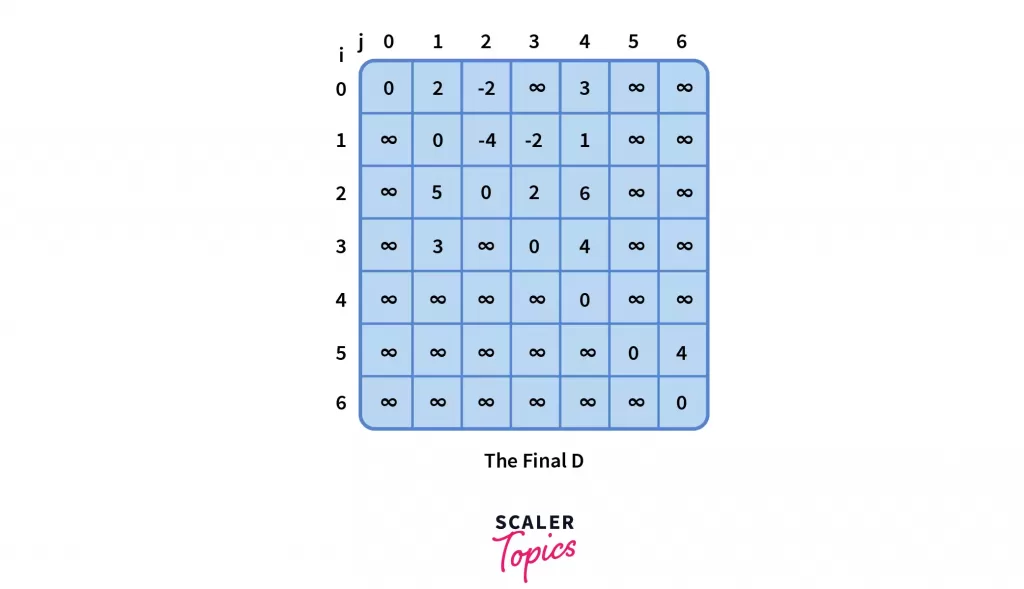
The Floyd-Warshall Algorithm
For the initial distance matrix D that we had earlier derived from adjacency matrix A of size nxn, we can formulate the above steps like so:
That’s it!
That’s the heart of the algorithm. 🙂
Three nested loops for k, i, j and one relaxation condition D[i, j] = min(D[i, j], D[i, k] + D[k, j]). Pretty straightforward I would say!
Q: So, what’s the catch?
A: The order of the loops.
None of the above works, because the iterator k responsible for intermediate nodes must always be in the outermost loop.
It’s because the Floyd-Warshall algorithm updates the distance matrix in incremental phases starting from k = 0.
So when k = 4, and both the inner loop completes their iteration, the distance matrix holds the shortest path by only considering nodes 0, 1, 2, 3, and 4 as the intermediate node.
In other words, prior to the kth phase, the value of any cell D[i][j] is equal to the length of the shortest path from node i to node j, if that path is allowed to enter only those nodes which are smaller than k.
In the end, the distance between any two nodes i and j refers to the shortest distance considering all possible numbers of intermediates in between.
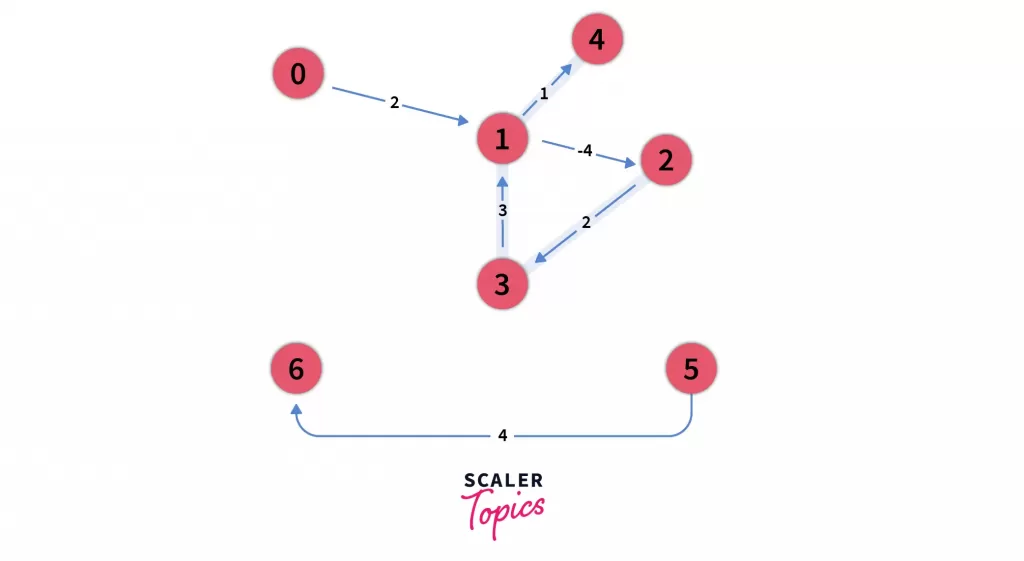
e.g. path from node 2 to node 4 hops through nodes 3 and 1
Let’s see what transpires when we alter the order of the loops?
Considering the order i –> j –> k, the shortest distance would be either a direct path or via only one intermediate node in between. That’s because we update all pairs of nodes only once.
However, there can be shorter routes from i to j if we consider multiple intermediate nodes as we have seen just before. Hence, by applying the correct order k –> i –> j (or k –> j –> i), we would be updating the routes k times for every pair of nodes.
I hope you have understood the algorithm now.
Whew… 🥲
That was a lot!
Speaking an infinite deal of nothing, shall receive the code in the coming section.
Live long and go through the language of your choice… 🖖🏻
Implementation of Floyd Warshall Algorithm on C, C++, Java, Python
Floyd Warshall Algorithm in C
Floyd Warshall Algorithm in C++
Floyd Warshall Algorithm in Java
Floyd Warshall Algorithm Python
Time Complexity of the Floyd Warshall Algorithm
The overall time complexity of the Floyd Warshall algorithm is where n denotes the number of nodes in the graph.
If you are not familiar with the analysis of complexity, you can go through here for details.
Since we are talking about time complexity, let’s address our unfinished discussion as to why the Bellman-Ford or Dijkstra’s shortest path algorithm is not an appropriate choice for solving the shortest path problem concerning all pairs of nodes.
The Bellman-Ford and Dijkstra’s shortest path algorithm only computes the shortest path from one node to all other nodes and has an respective upper bound of and where and are the numbers of nodes and edges respectively.
Moreover, Dijkstra’s shortest path algorithm doesn’t work for negative weighted edges.
And if we extend the Bellman-Ford algorithm for all nodes, the time complexity becomes = .
We know, the maximum number of edges can be a high as for a directed graph, so the overall complexity could be as high as but since the Floyd Warshall algorithm depends only on the number of nodes, the number of edges does not matter.
This makes the Floyd-Warshall algorithm a more efficient choice!
Applications of the Floyd Warshall Algorithm
So far, we have only been talking about one use case of the Floyd Warshall algorithm. Here are few applications mentioned below:
- Fast computation of Pathfinder networks
- Inversion of real matrices
- The transitive closure of directed graphs
- Checking if an undirected graph is bipartite or not.
- Shortest path in a graph
Join Dynamic Programming Course by Scaler Topics to master advanced problem-solving techniques and enhance your programming prowess.
Conclusion
The Floyd-Warshall algorithm is one of the shortest path algorithms for graphs in that you can apply its properties to solve the above-mentioned problems.
