Heap Data Structure

Heap Data Structure is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. Min-Heap − Where the value of the root node is less than or equal to either of its children. Max-Heap − Where the value of the root node is greater than or equal to either of its children.
What are Complete Binary Trees?
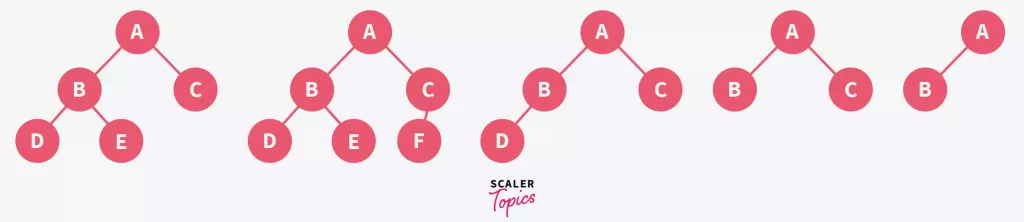
Complete binary trees are structured such that:
-
Fully Filled Levels: Each level is completely filled, with the possible exception of the last level. This ensures a dense and balanced tree structure.
-
Left-Filled Last Level: The last level is filled from left to right, which might not be fully complete, maintaining the tree's integrity.
-
Sequential Arrangement: Elements are arranged sequentially without gaps, adhering to the parent-child index relationship, crucial for representing the tree as an array.
-
No Empty Spaces: True complete binary trees don't have empty spaces in their array representation, making each position meaningful.
Incorrect Array Representation:

Correct Array Representation:

- Foundation for Heaps: This well-ordered structure is essential for forming heaps, ensuring they meet the necessary criteria for max-heap or min-heap in data structure, based on the heap property.
Types of Heap Data Structure
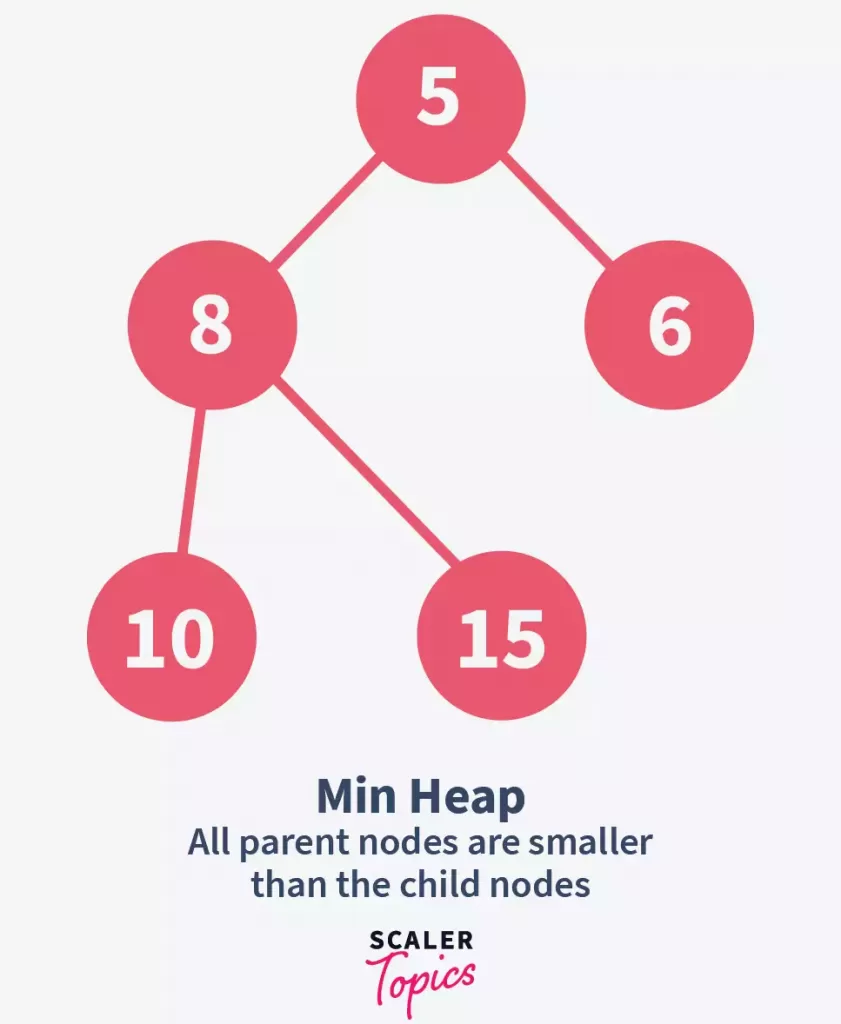
1. Min-heap:
- In a min-heap, each node is smaller than its child nodes.
- The root of a min-heap is the smallest element in the heap.
The provided image shows a min-heap example: the root 5 is smaller than its children 8 and 6, and node 8 is smaller than its children 10 and 15, confirming the min-heap structure.
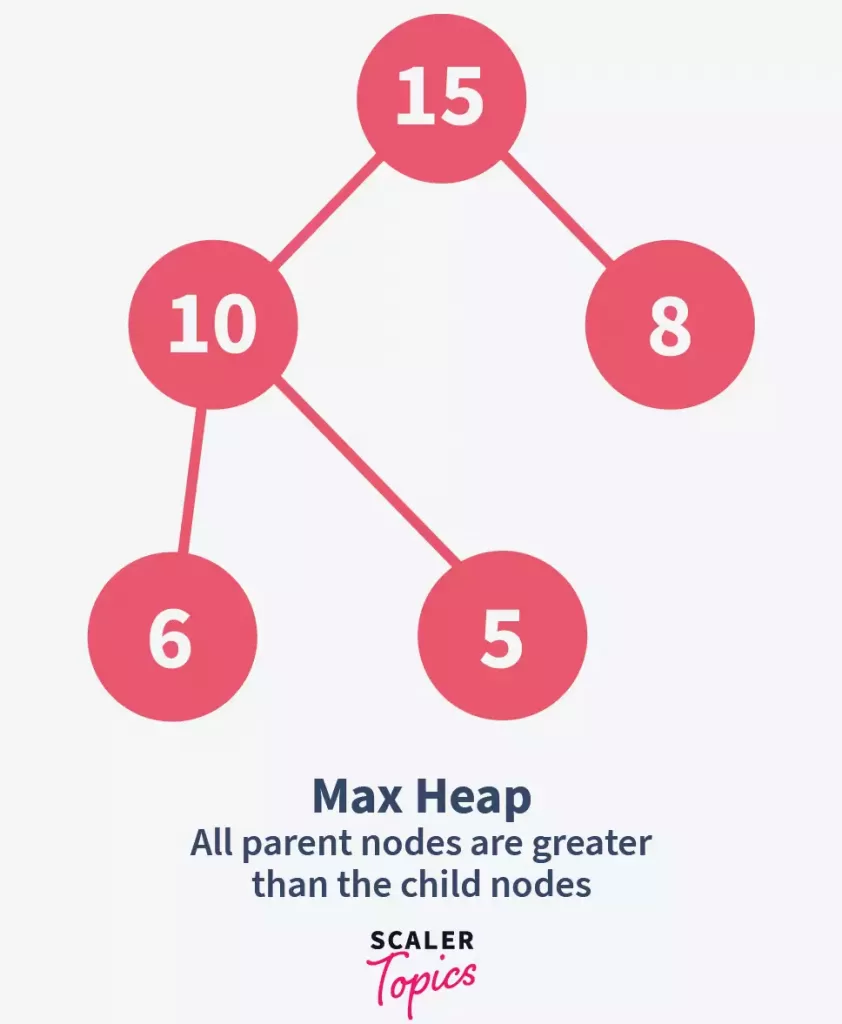
2. Max-heap
- In a max-heap, each node is greater than its child nodes.
- The root of a max-heap is the largest element in the heap.
The provided image illustrates a max-heap example: the root 15 is greater than its children 10 and 8, and node 10 is greater than its children 6 and 5, confirming the max-heap structure.
Heap Data Structure Operations
Every data structure has some operations like insertion, deletion associated with them. Heaps are no different, and there are many operations that can be performed on heap data structures. We will be discussing these operations over a max-heap since the same operations can be applied to a min-heap also.
Heapify
Heapify process for a binary tree involves transforming an array into a max-heap in data structure by ensuring every parent node is larger than its children. Consider the steps using the array 10, 8, 5, 15, 6:
-
Visualize the Array as a Complete Binary Tree: Convert the array elements into tree nodes, maintaining the structure of a complete binary tree.
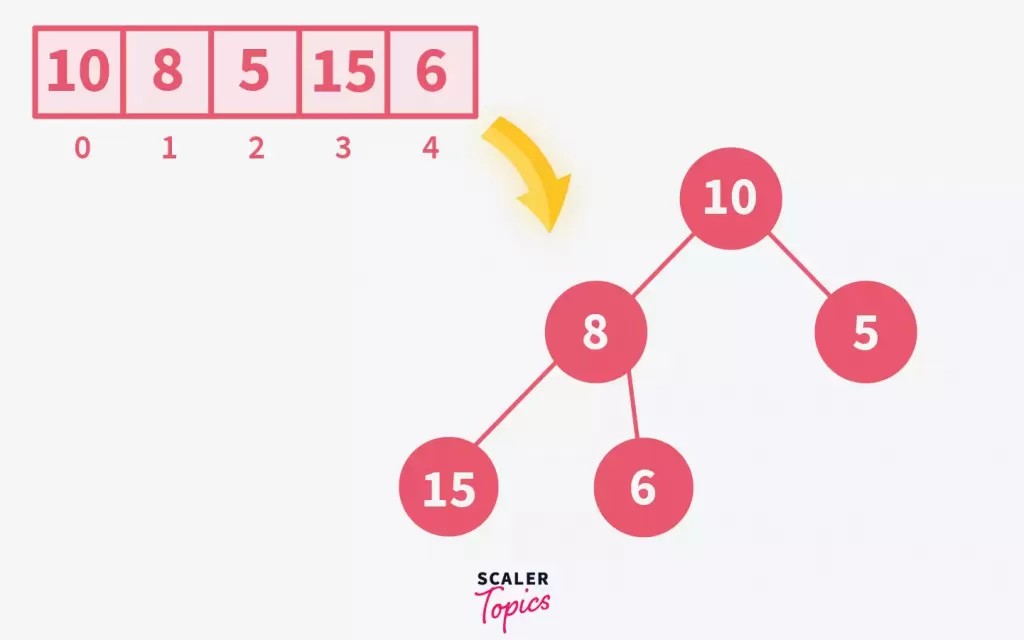
This tree isn't a max-heap yet since node 8 is smaller than its child 15.
-
Heapify the Tree: Compare parent nodes with their children, swapping the parent with the larger child if the parent is smaller. Repeat this until every node follows the max-heap property.
Start with node 8, comparing it with children 15 and 6. Swap 8 with the larger child, 15.
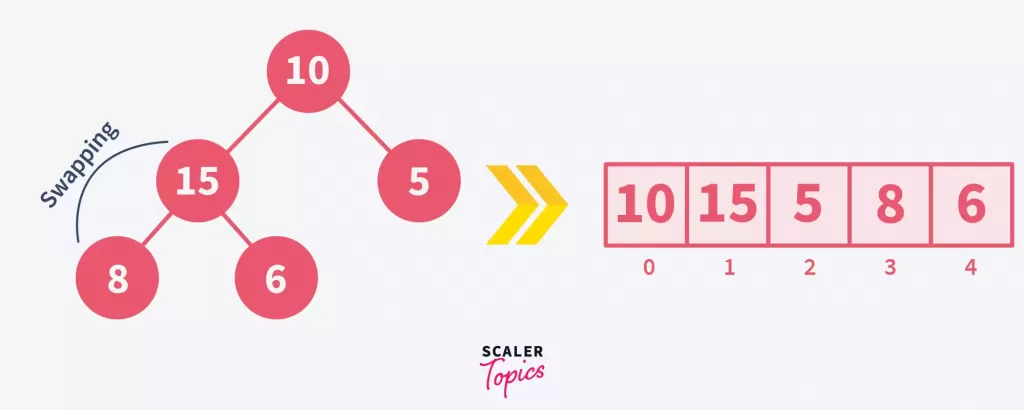
Continue heapifying up the tree. Since 15 (now a parent) is larger than 10, swap them to maintain the max-heap property.
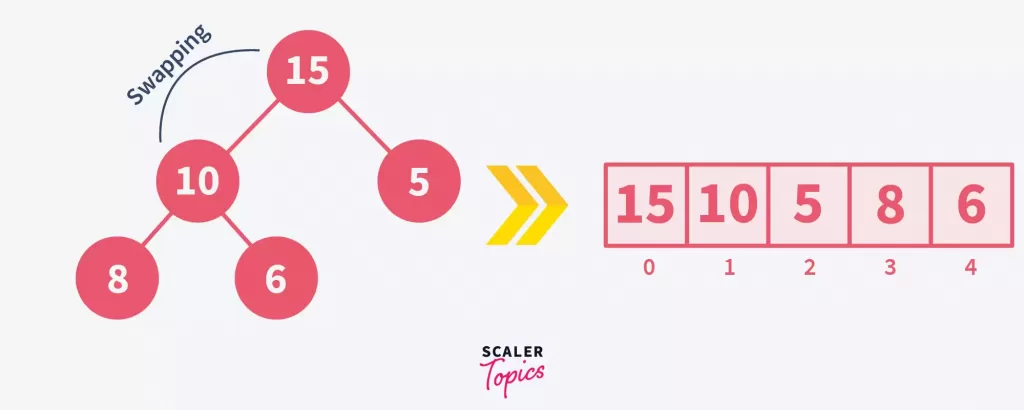
Heapification works bottom-up, ensuring all children are heapified before their parents. This recursive approach, starting from the lowest sub-trees, optimizes comparisons and adheres to a time complexity of O(logn) per node, due to the tree's height determining the maximum swap operations.
Insertion in Heap
To insert elements into a heap and build a max-heap from the array 10, 8, 5, 15, 6, follow these optimized steps:
-
Start with the First Element: Insert 10 as the root. This forms the beginning of your heap.

-
Insert the Second Element: Add 8. Since 10 > 8, no swap is needed. The heap property is maintained.

-
Continue Adding Elements: Insert 5 next, keeping the tree structure.
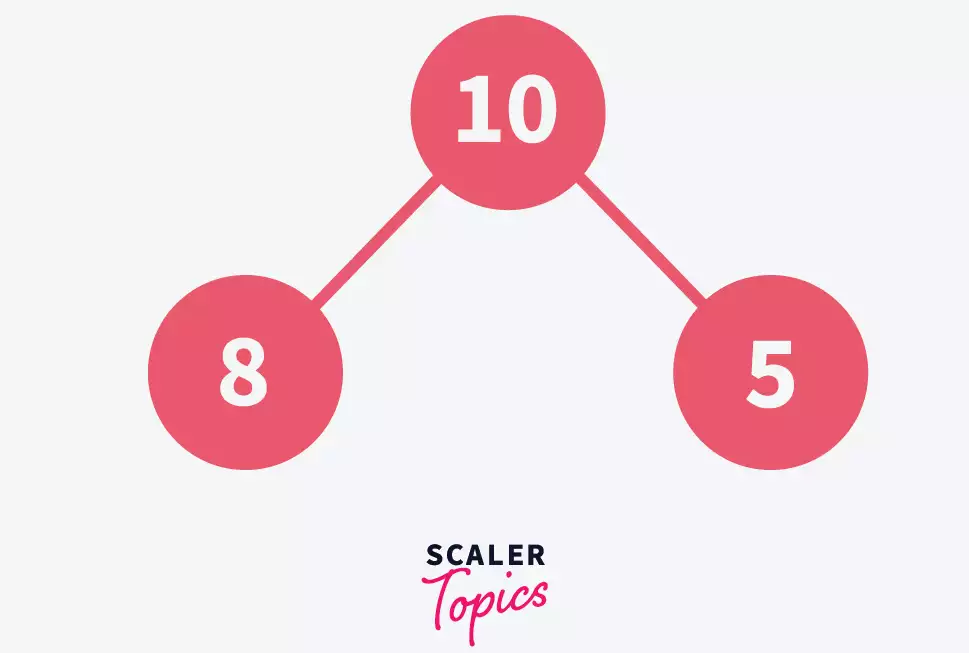
-
Insert 15 and Adjust: Adding 15 requires adjustments. Swap 15 with 8, then 15 with 10 to maintain the max-heap property, demonstrating the "bubbling up" process where elements find their correct position.
- After first swap:

- After second swap:
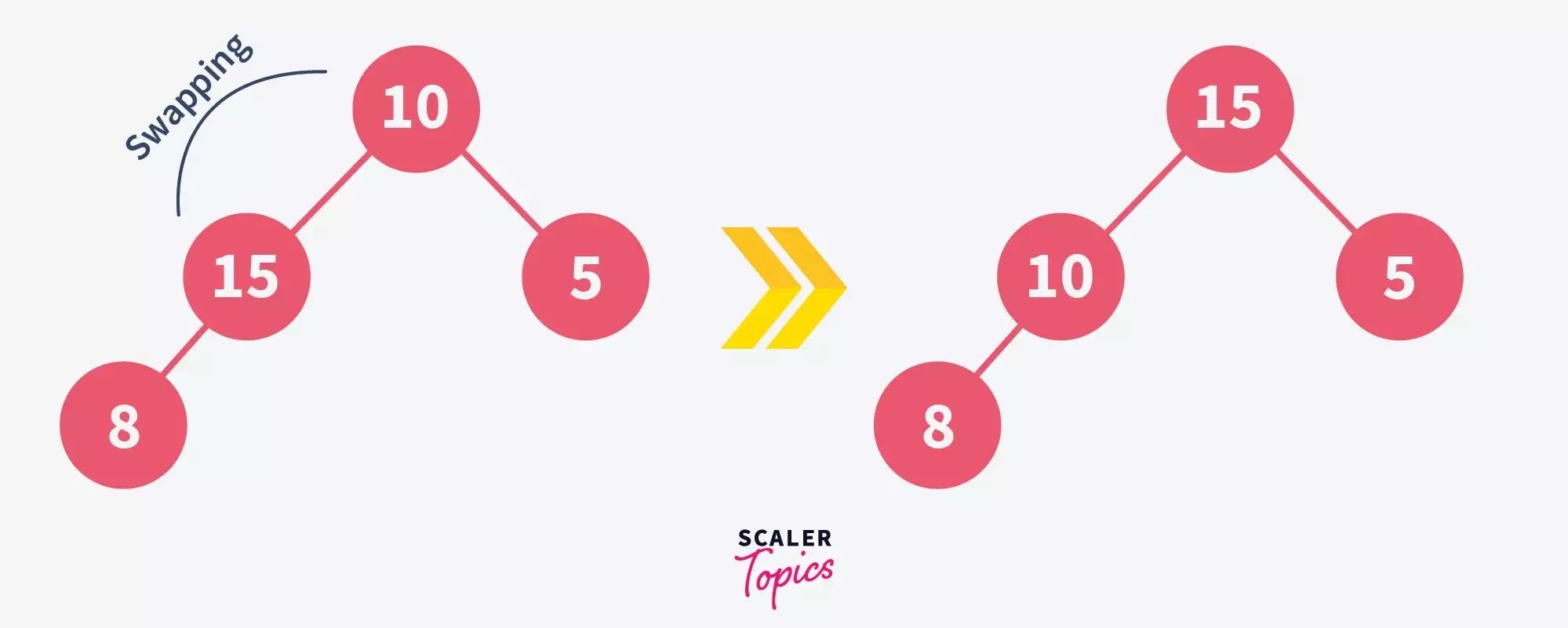
- After first swap:
-
Add the Final Element: Place 6 in the heap, comparing it with its parent to ensure the heap's integrity.
This insertion process involves comparing each new element with its parent and swapping if necessary, ensuring the max-heap condition is always met. The "bubbling up" ensures elements are positioned correctly, maintaining the heap structure. While comparisons depend on the tree's height, leading to a potential O(nlogn) complexity, optimizing with heapify can reduce this by reordering the heap in a bottom-up manner after all elements are added, improving efficiency.
Deletion from Heap
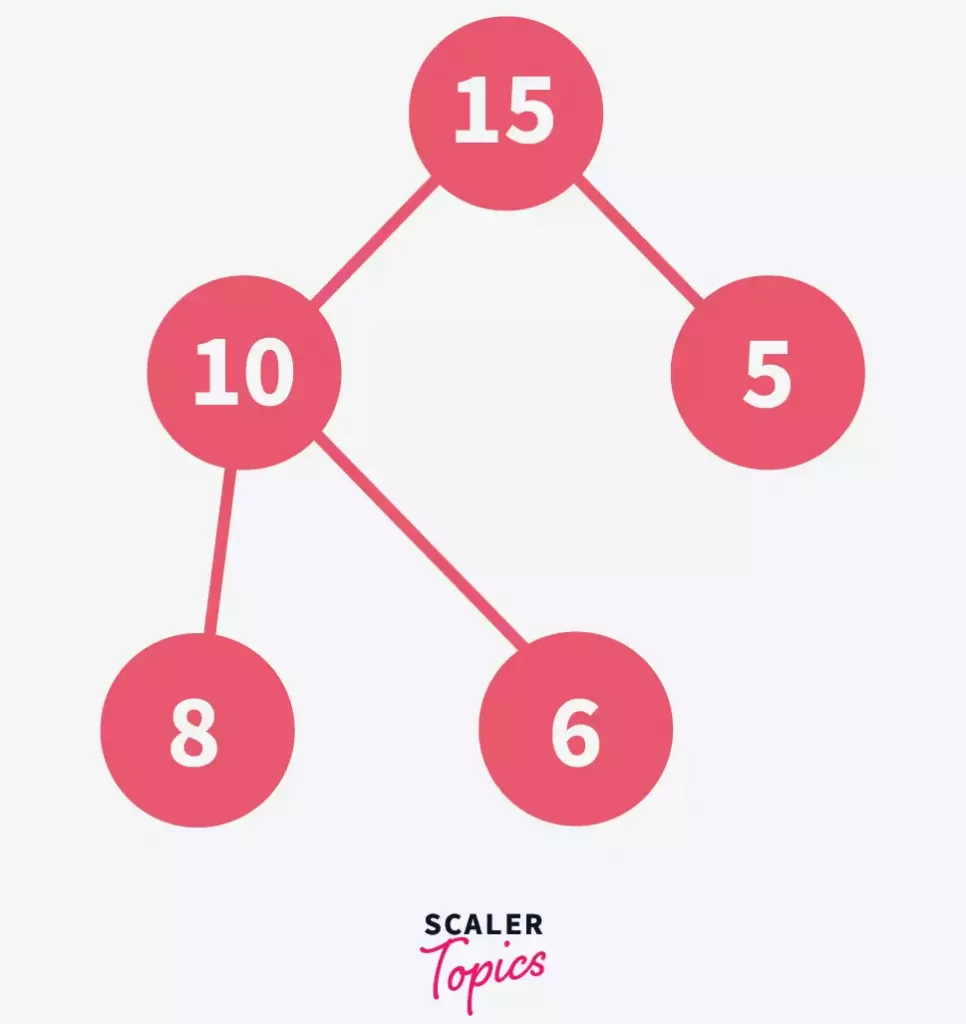
Let us consider the following max-heap that we created in the last step-

To delete the elements from a heap, we follow the under-given steps –
-
Search for the element to be deleted and swap it with the last element in the heap, let’s say we want to delete 10-
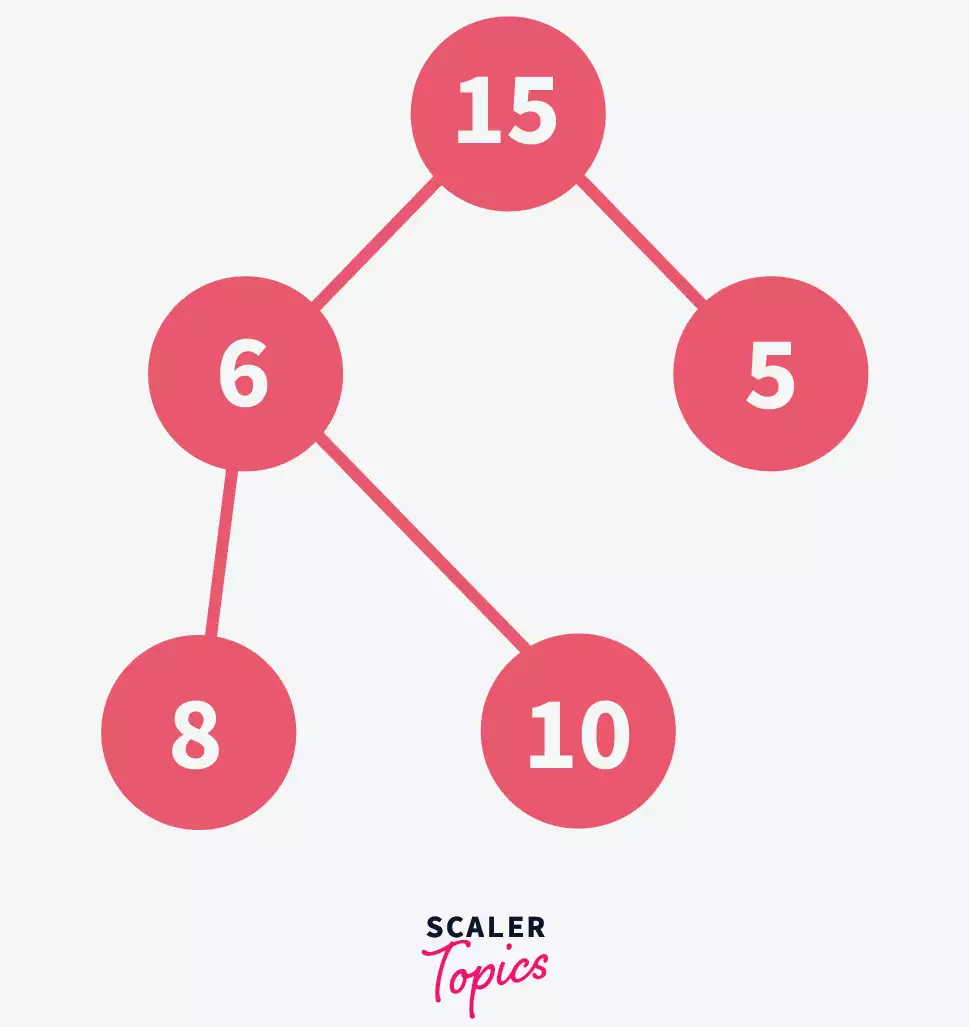
Here, we have swapped the position of 10 with the last element that is 6
-
Remove the element from the tree –
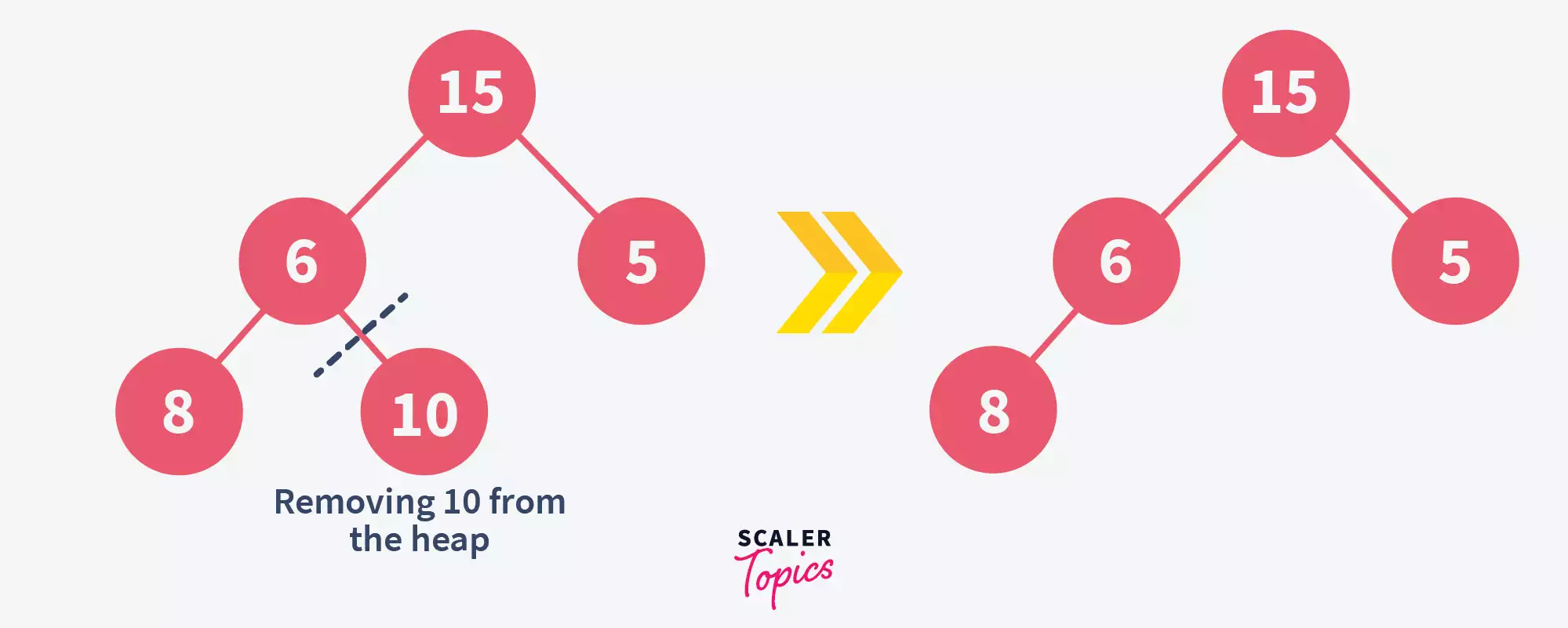
But now, the remaining heap is not a max-heap anymore. So, as the next step, we should heapify it once again.
-
Heapify the tree again-
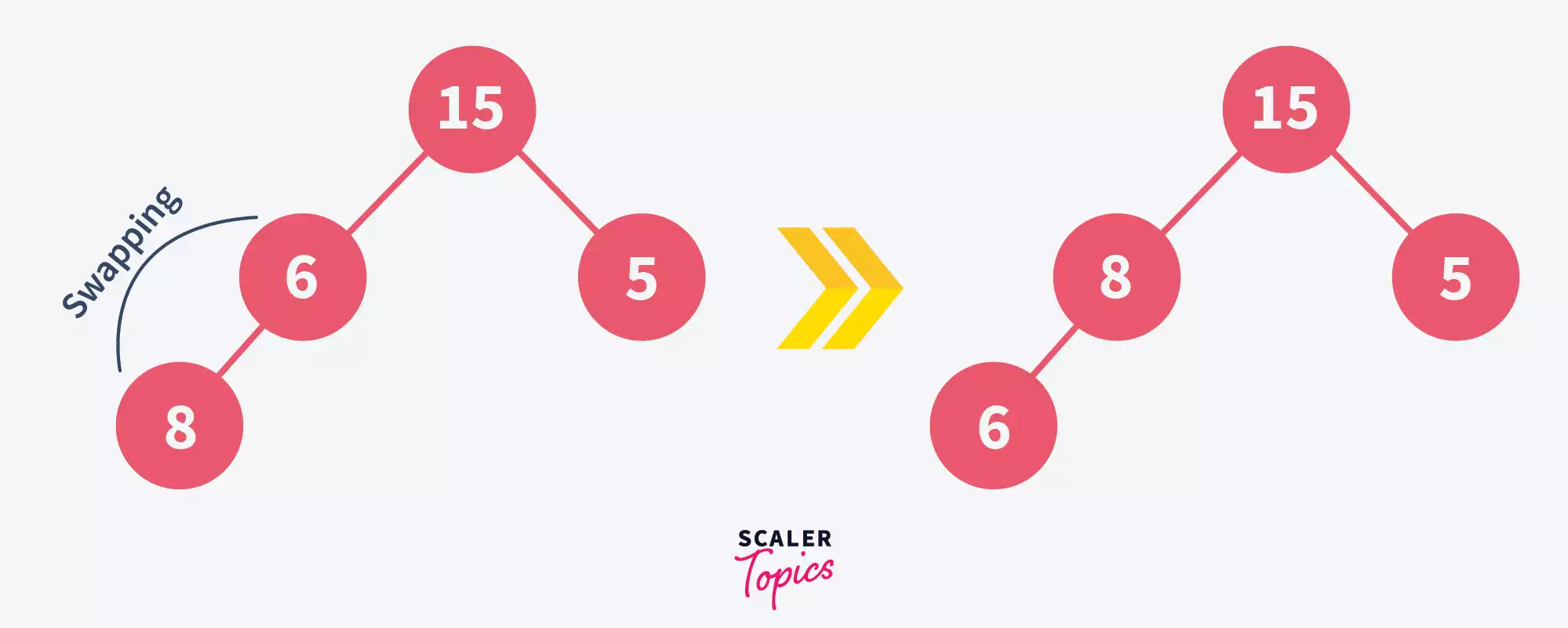
Here, we have once again heapified the given tree to form a max-heap.
Thus, we have successfully removed 10 from the heap.
Peek
The Peek operation in heap data structures retrieves the topmost value— the maximum in a Max Heap or the minimum in a Min Heap—without modifying the heap. This is done by accessing the root node's value, typically stored at the beginning of the underlying array or the top of the tree structure representing the heap.
Implementation of Heap
1. C
2. C++
3. Python
Unlock the Power of Efficient Coding! Join Scaler Academy's DSA Course Today and Transform Your Problem-Solving Abilities.
Conclusion
- Heap in data structure efficiently organize data in Min-Heaps and Max-Heaps, optimizing access to the highest or lowest elements.
- Inserting elements into a heap involves comparisons and potential swaps to keep the structure intact, following a "bubbling up" method.
- Deletion involves swapping the targeted element with the last, removing it, and then re-heapifying to maintain order.
- The Peek operation grants immediate access to the heap's top element without disturbing the overall structure, crucial for quick data retrieval.
