Line Sweep Algorithm

Overview
The line sweep algorithm is based on the idea of using a vertical imaginary line that moves in the rightward direction upon the occurrences of certain events defined by the current problem at hand. The line sweep algorithm is used to solve problems such as closest pair, line segment intersections, the union of rectangles, convex hull, Manhattan minimum spanning tree, and more.
What is Sweep Line Technique?
Before moving on to the sweep line algorithm, let's understand the "sweep line" first. A sweeping line is essentially a vertical line that is "swept" across the plane rightwards. You can visualize it as an imaginary vertical line on a piece of graph paper. It is called the sweep line because we sweep it in the right direction based on the occurrence of certain events. You'll get a clearer understanding further in the article.
In this article, we will talk about three other terms - Euclidian distance and Manhattan distance Let's quickly go through these terms for an easier understanding of this article.
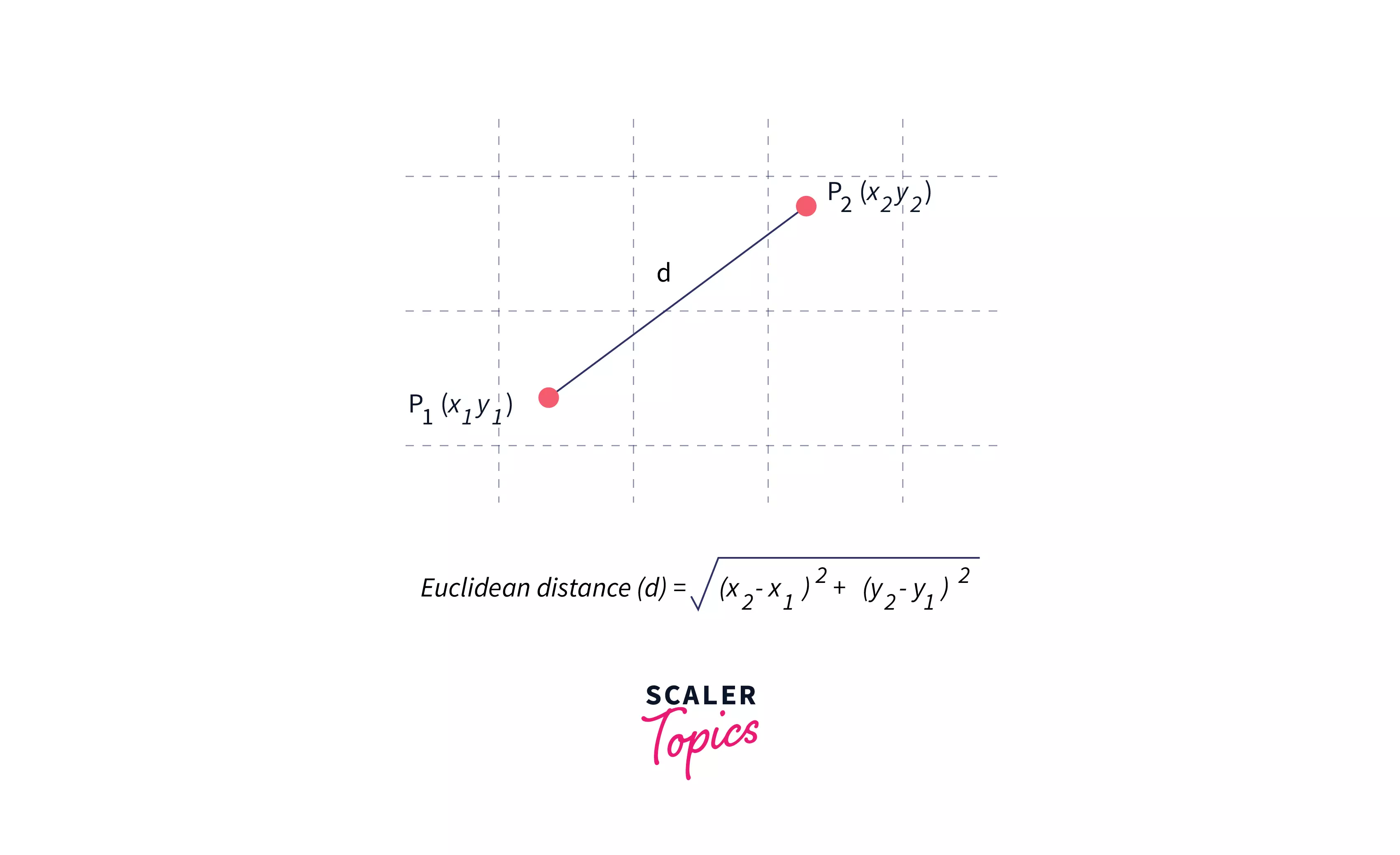
The Euclidian distance is simply the distance between two points when calculated by making use of the Pythagoras theorem. It is given by the square root of (x1 - x2)2 + (y1 - y2)2.
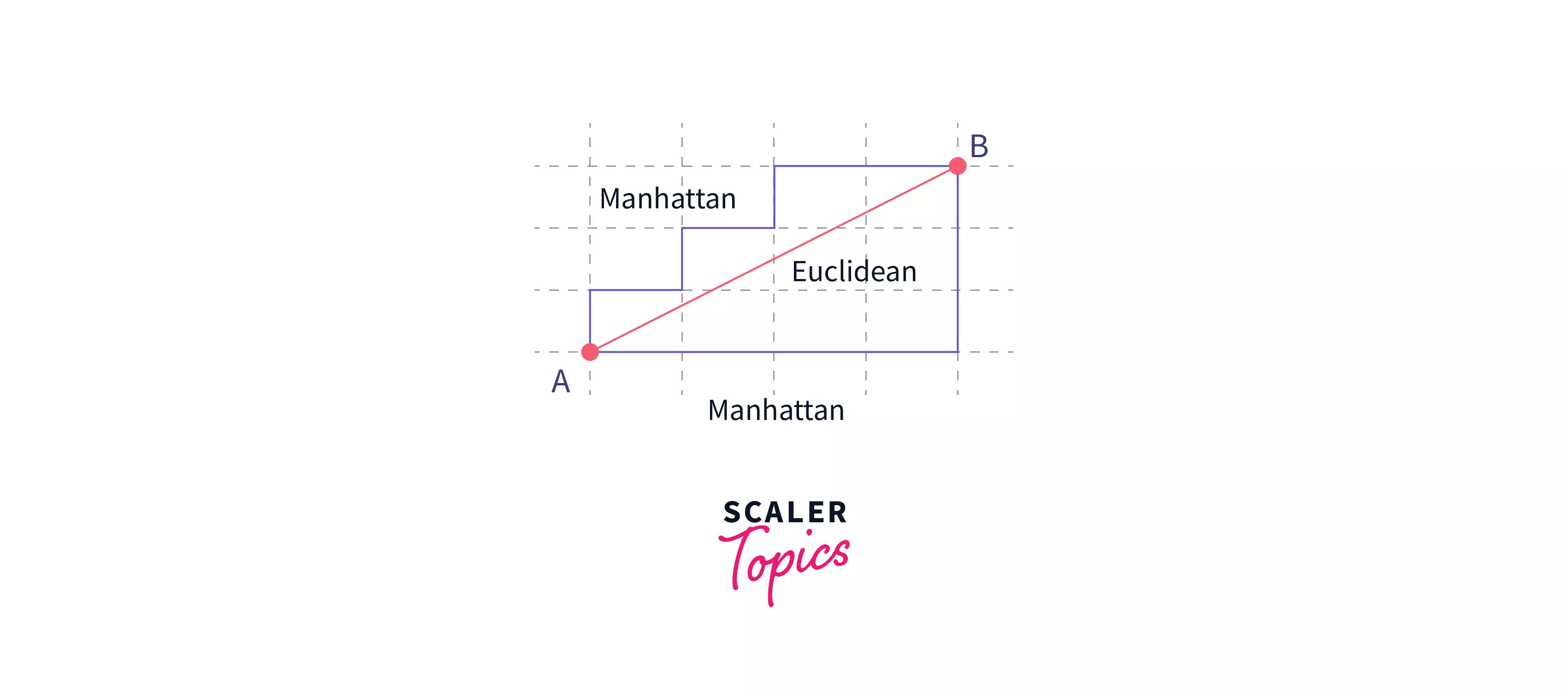
Manhattan distance is the distance that is travelled when you're either moving only vertically or only horizontally. It is given by - |x1 - x2| + |y1 - y2|.
Coming back to the sweep line, all the algorithms that make use of the sweep line concept are called line sweep algorithms or plane sweep algorithms. As we read before this line is swept on the plane when certain events occur, to discretize the sweep and these events will be based on the current problem at hand.
These will be discussed further in the article below. Other than the events based on the problem, we must also maintain a data structure for problems based on this technique, and in c++ we make use of the set.
Let's now look at certain problems that use the line sweep algorithm.
Closest Pair
The first problem is the closest pair problem. The problem statement states that:
You are given a set of points, and you must find the pair of points that are closest to each other.
Of course, you can solve this problem by the brute force solution which involves considering all the pairs of points but the time complexity of this solution would be O(N<sup>2</sup>) as you would make use of 2 for loops to iterate over all the points, finding the distance. Using the line sweep algorithm, you can reduce this time complexity to O(NlogN).
Let's see how we will solve this problem using the line sweep algorithm. Say you have all the points processed 1 to N - 1 that are ordered by X since we want our line to move in the X direction toward the right and the shortest distance that you have found between 2 points till now is h. Now for the Nth point we would have to find points whose distance from the Nth point is either less than, or equal to 'h' to find the closest pair.
We are aware that we can go only till distance 'h' from the point xN to find such a point, and in the vertical direction as well, we can go 'h' distance upwards and downwards. This gives us a particular set of points that we will consider to find the closest pair.
The set of points whose x coordinates lie in between [xN - h, xN] and y coordinates lie between [yN - h, yN + h]. All the points that have x coordinates that are less than xN - h must be deleted since the distance between xN and that point would be greater than h. Once we are done with these processing steps, we will add the Nth point to the set.
Once we have all our points in the set, we would calculate the distances and find the closest pair.
Let's take a look at the example using this algorithm.
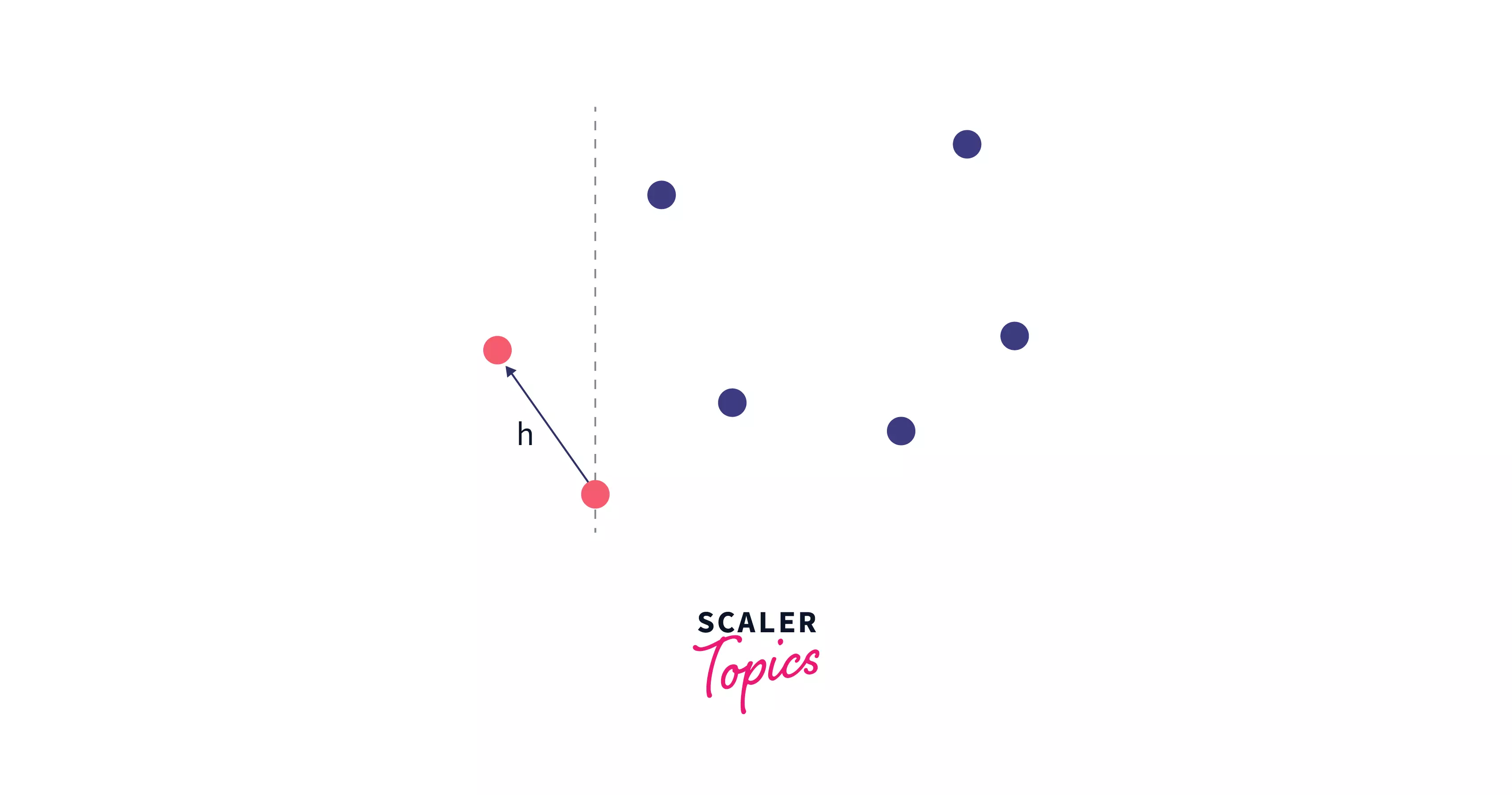
Here, we have our vertical sweep line and the first shortest distance between the first 2 points on the place - h. We will update this value of h if the new distance between two points is less than h since we want to find the minimum value of h which will define the closest pair of points.
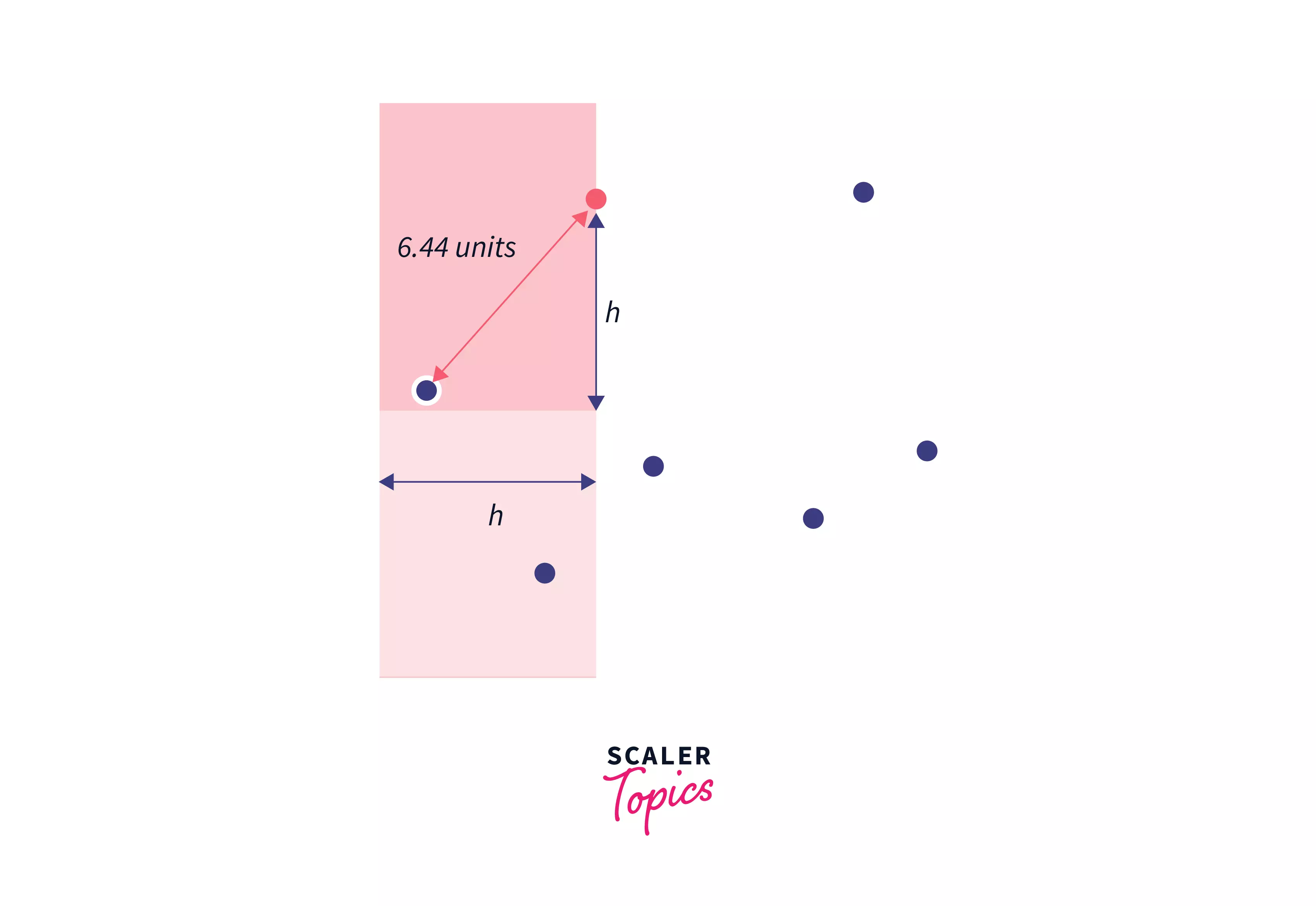
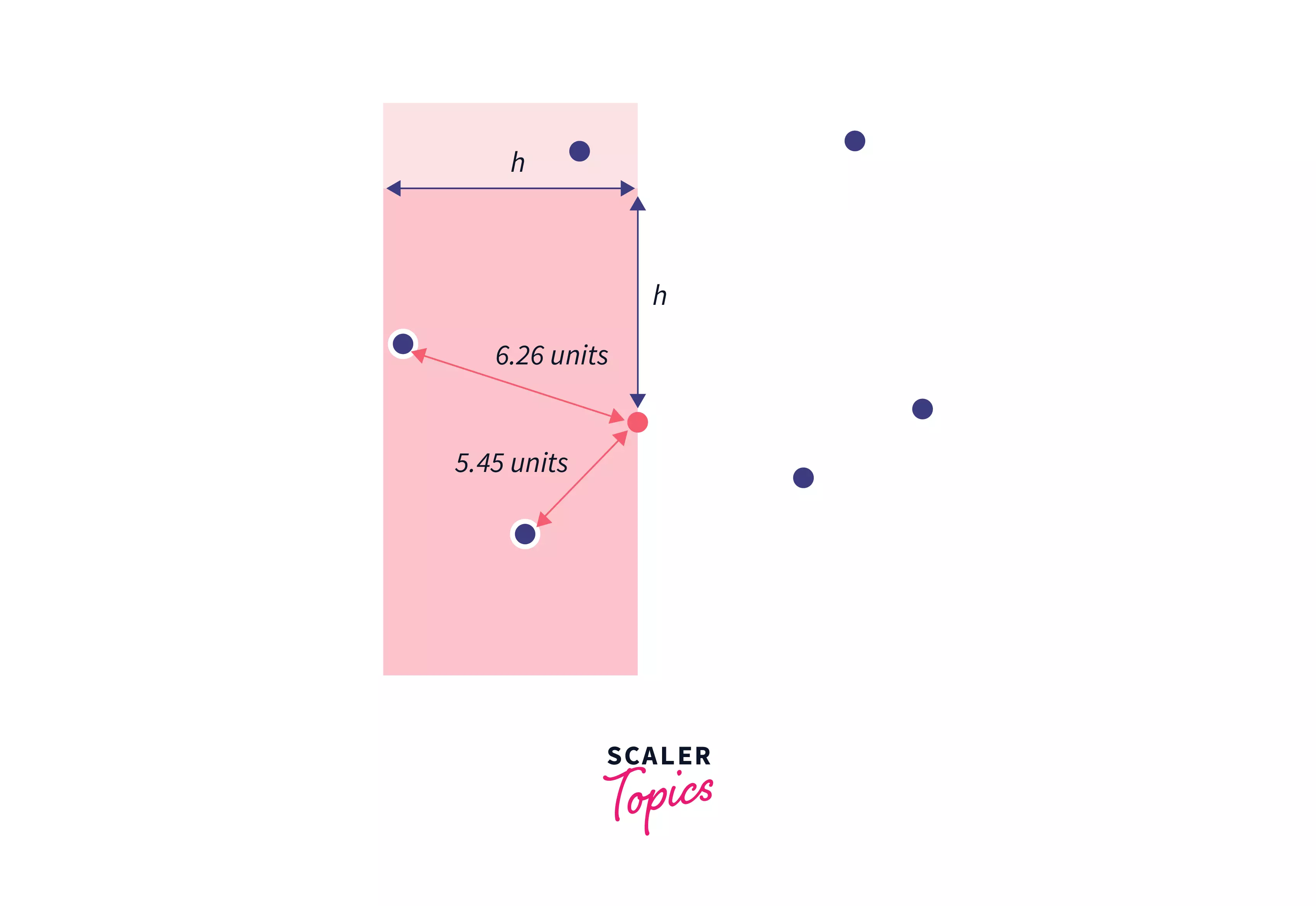
In these images, the red shaded region is the set that has points that fall under the coordinates as we discussed before. All the points which lie on the left region of this red area are deleted from the set. As we find lower values of h our line is swept towards the right in the plane.
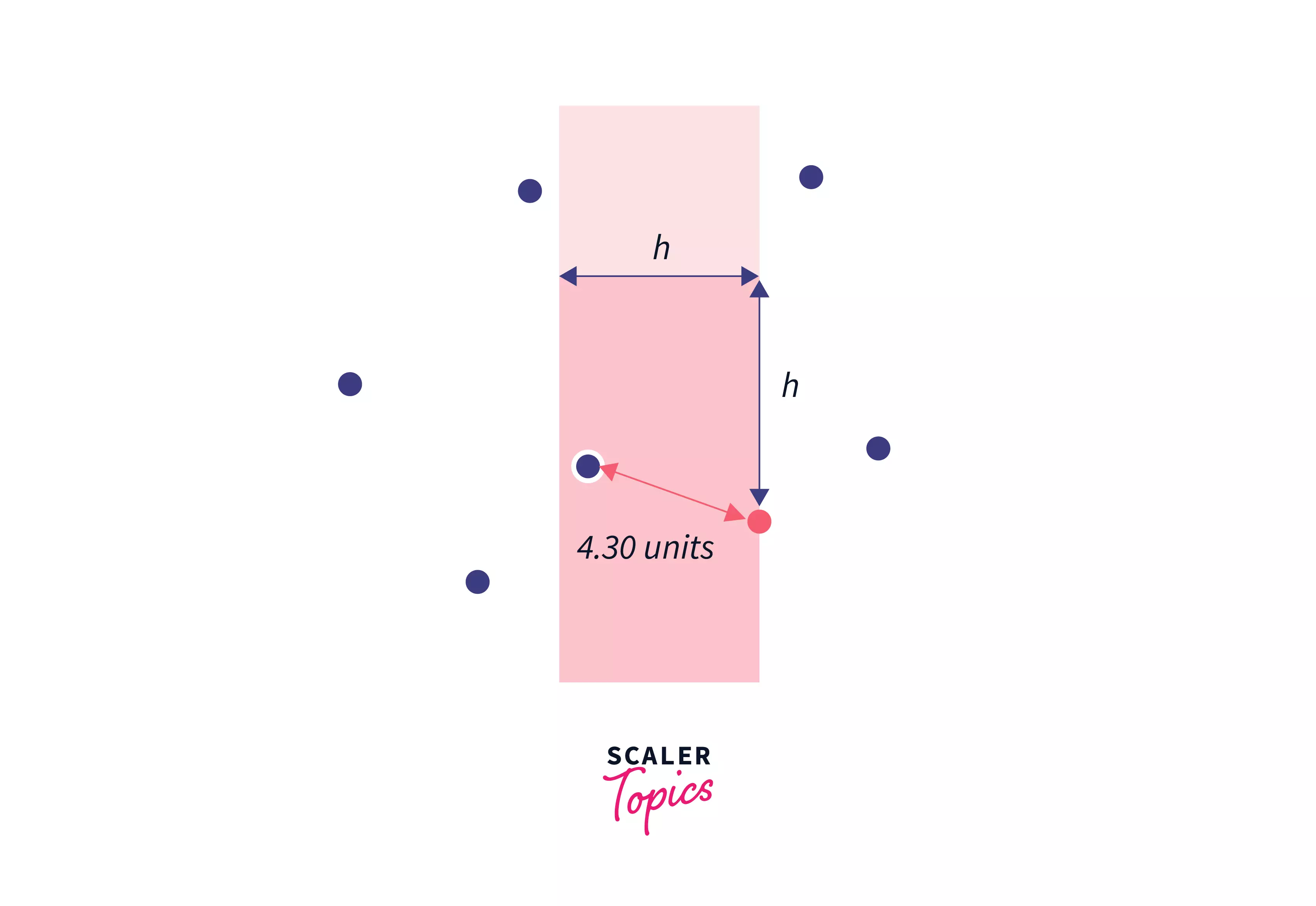
Let's discuss the algorithm:
- Initially, we must sort all the points based on the x coordinates since our line will be swept along the x-axis, i.e. in the rightward direction.
- After this, the first point from the points array will be inserted into the set.
- We will loop over each point in the set, we will remove all the points to the left of the current point whose x coordinate has a distance more than h from xN. The time complexity for this loop will be O(N) since we have N elements in our set. The deletion of points that have a distance greater than h from xN will have a time complexity of O(logN) making the overall time complexity of the loop - O(NlogN).
- We next need to iterate over all the points that lie in the set of points whose x coordinates lie in between [xN - h, xN] and y coordinates lie between [yN - h, yN + h]. O(logN) time is required to find the lower bound where 'h' is the minimum distance between 2 points found so far.
- For each point we will insert it into the set and this will take O(logN) time.
Hence, we have found the closest pair in O(N*logN) time. Using the algorithm above, write code in your preferred language.
Line Segment Intersections
Moving on to our next problem that can be solved using the line sweep algorithm, we have the line segment intersection problem. The task is to find all the intersections of horizontal and vertical lines.
Now, a few obvious observations about line segments. Horizontal lines will not have a single X coordinate, hence while approaching the solution, sorting by X coordinate is not a good idea. Instead, we now have an idea of the event at which the line must be swept - the X coordinate at which something happens. This "something" could be - a vertical line, the start of a horizontal line, or the end of it. With the movement of the sweep line to the right, we will maintain a set of all the horizontal lines that were cut by the sweep line which would be sorted by their Y value. Take a look at this figure:
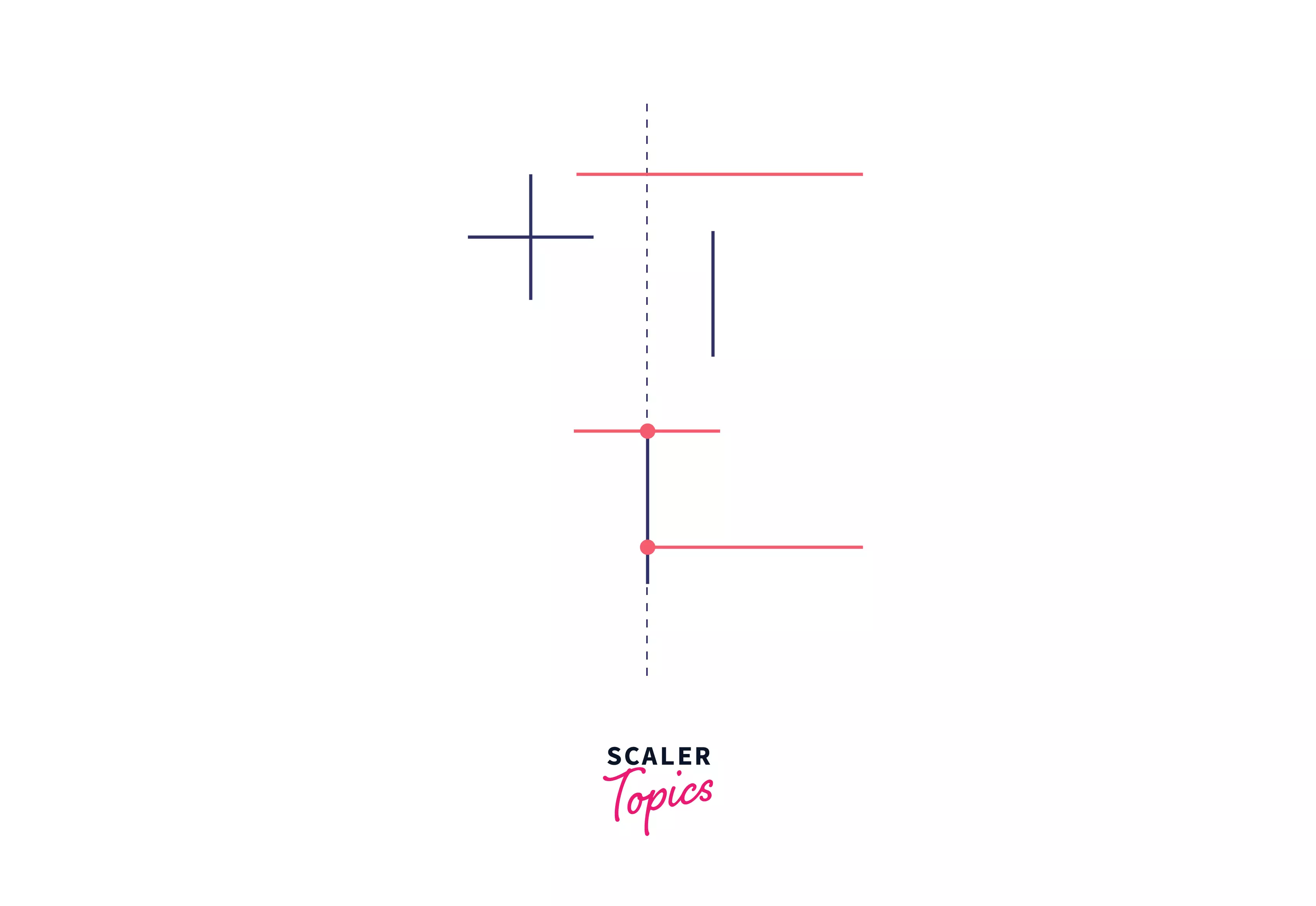
The red lines in the figure are all those lines that were cut by the sweep line, sorted by the Y value. Now, since we are working with lines, and to find out the intersections of the lines, we must know where they start and end at. So, to handle the start of a horizontal line or the end of it, we would just need to add (if a line starts) or remove (if a line ends) an element (the point of start or end of a line) from the set that we are maintaining.
The addition and deletion of an element from the set would cost us O(log N) time. Upon hitting a vertical line, if we perform a range search (over the vertical line) i.e. look for other horizontal lines that cut the current vertical line, we can immediately find out the horizontal line that it cuts or intersects with.
So here's how this works:
- Our sweep line initially starts from the leftmost end, and that is when we add the lines to the set (if horizontal).
- When our sweep line moves towards the right we simply remove the horizontal lines that fall to the left of it.
- Upon encountering a vertical line, we perform a range search on the line with the lines in the set to find the interactions.
- This process is repeated.
If only the intersections are required, we can work with this algorithm that gives us a time complexity of O(NlogN + I) for the I number of intersections.
If we take a more general case, the lines might not be only horizontal or vertical. Here, it would not make sense if we had our events pre-sorted, like in the case when the lines were only horizontal or vertical. We would have to make use of a priority queue and upon encountering intersection events between lines we would add or remove them dynamically to the queue.
So that way, at any point in time, our queue would not only contain the start and endpoints of the line segments, but also the intersection points of the adjacent elements that are present in the active set (priority queue).
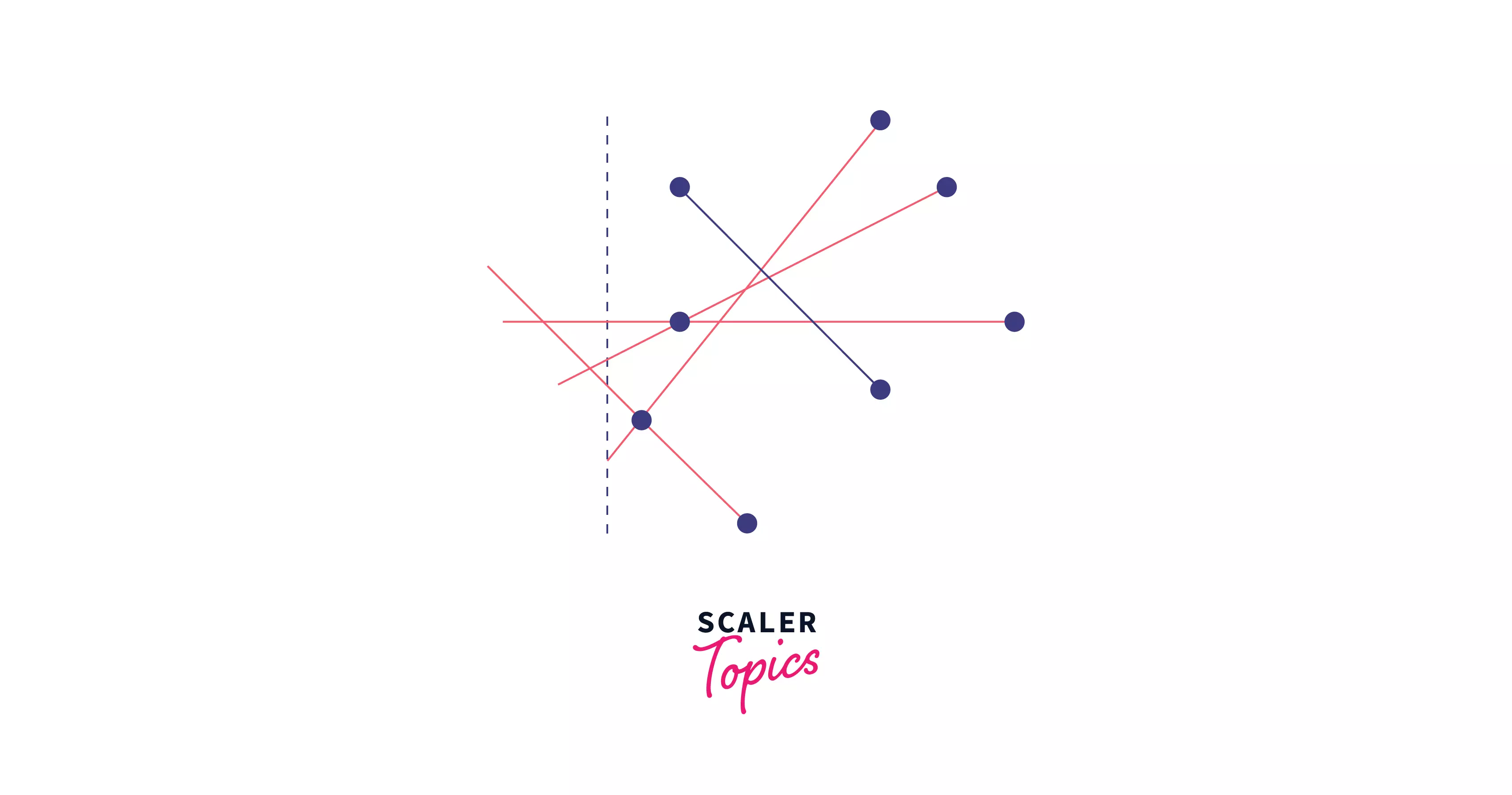
Here, all the red lines are a part of the active set since they are in contact with our sweep line and the black lines are not.
Union Of Rectangles
Coming to the next problem that can be solved using the line sweep algorithm is the union of rectangles. The problem statement is:
You are given a set of N axis-aligned rectangles, i.e. the edges of rectangles are parallel to either the X-axis or the Y-axis. You are required to find the area of the union of all these rectangles.
A rectangle would be represented by two points - the lower-left point and the upper right point.
So what would be our events?
Just to revise, events are those circumstances when our sweep line moves towards the right.
Of course, our events would be when a rectangle starts or ends, i.e. vertical edges. Upon encountering the left edge, we perform some actions and upon encountering the right edge we perform other actions. As we know, our left edge would be represented by the lower-left point and the right edge would be represented by the upper right point.
We can start by sorting the events by their x coordinates. Hence, upon encountering a left edge of a rectangle we can insert that rectangle into our active set. When we encounter the right edge of a rectangle, i.e. our sweep line has "swept" over the rectangle, we will delete it from the active set. At any point in time, the only rectangles that intersect with the sweep line will be present in the active set.
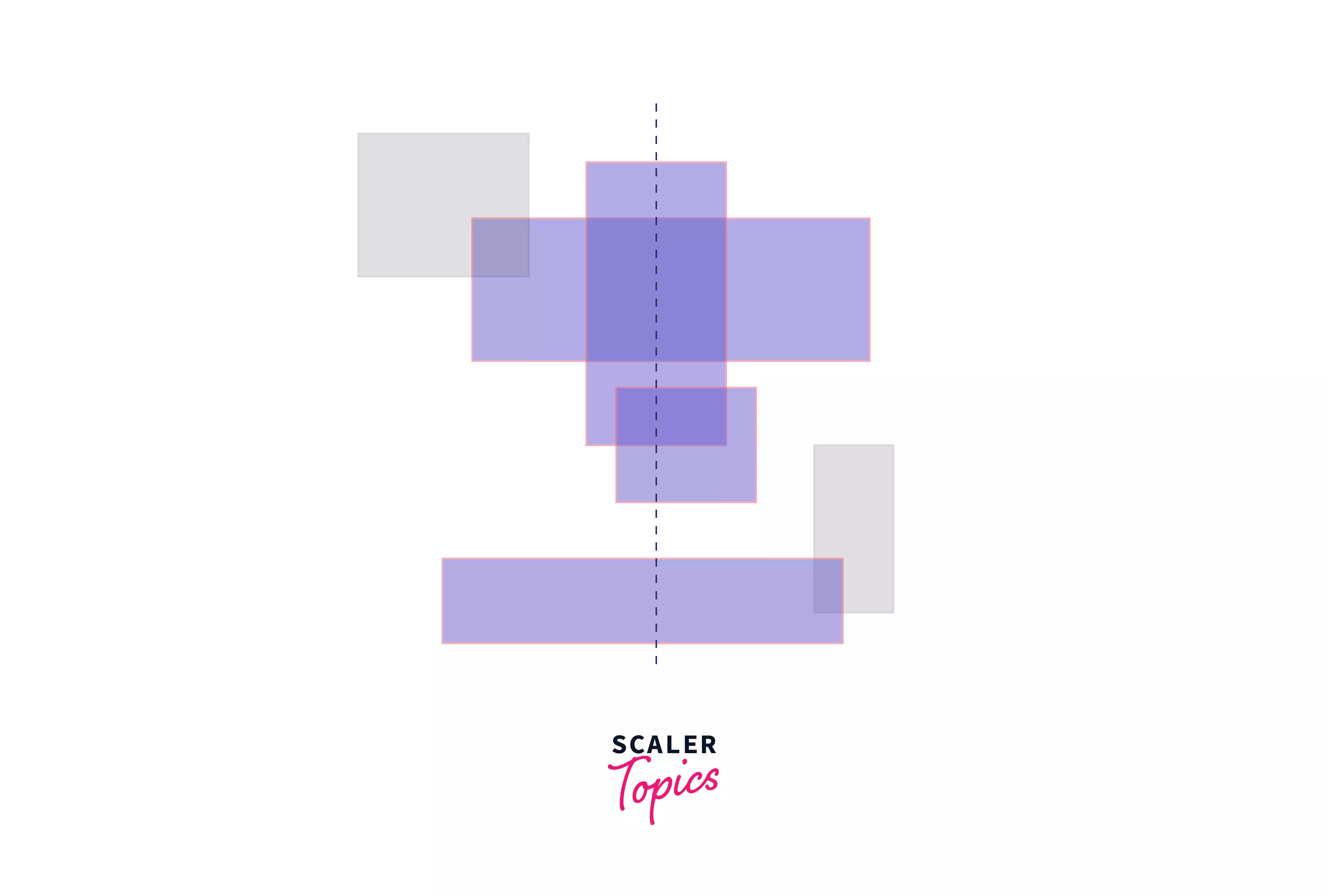
Again, as you can see, the rectangles with a red outline will be a part of the active set, while the rectangles with the black outline will not be a part of the active set since the sweep line does not intersect them.
So, we are aware of the rectangles that are cut by our sweep line, but to be able to calculate the area we must also be aware of the length of the sweep line that is cut, i.e. the length of the solid blue segments that can be seen in the image. When we calculate the length of the blue segments we can simply multiply this with the horizontal distance between the events (left and right points).
This can be achieved, but with a slight change, instead of having our sweep line vertical, we have a line swept horizontally from the bottom towards the upper part of the plane. Now, the events at which we sweep our line would change as well.
The events would be the horizontal edges of the active rectangles (an active rectangle would be a rectangle cut by the vertical sweep line). Upon encountering the bottom edge of an active rectangle, we would increment a counter (this counter variable would maintain the count of rectangles that are overlapping currently) and we decrement this counter when we come across the top horizontal edge of the active rectangle.
When the counter changes its value to zero from some non-zero value we would have found the length of the area that is cut on the vertical sweep line (the solid blue line segment as discussed earlier) and that is how we add the area to our final answer.
Here's how it works:
- For all the events of our vertical sweep line, we are required to find the length of the "cut" of that sweeping line.
- To find this length, we create a horizontal sweep line, that moves in a bottom-up manner. We can make use of a boolean array as a data structure as we would first have sorted the rectangles based on our vertical sweep, and the second time in order of the horizontal sweep.
Here's how the algorithm runs:
1:
 2:
2:
 3:
3:
 4:
4:
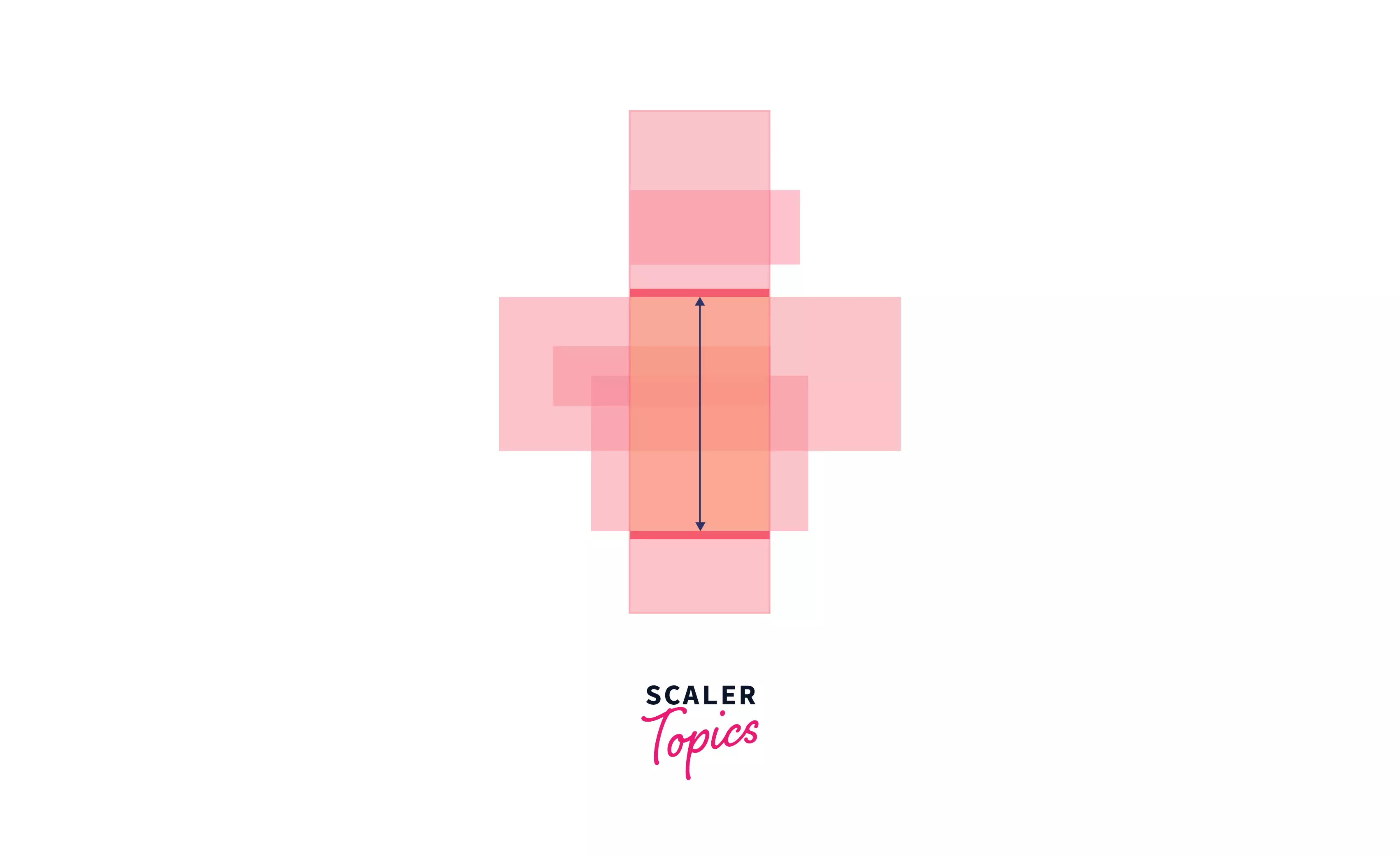 5:
5:
 6:
6:
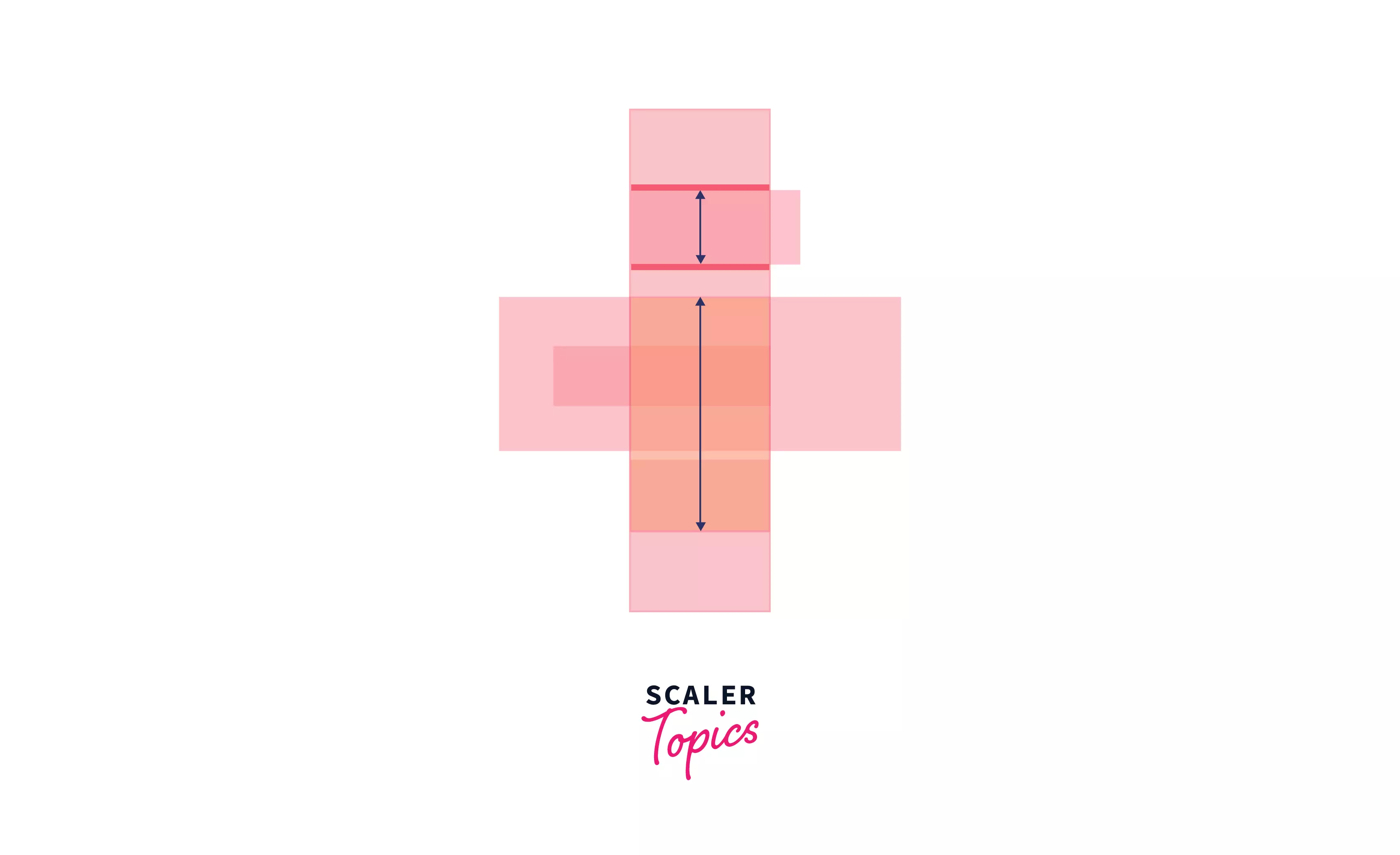 7:
7:
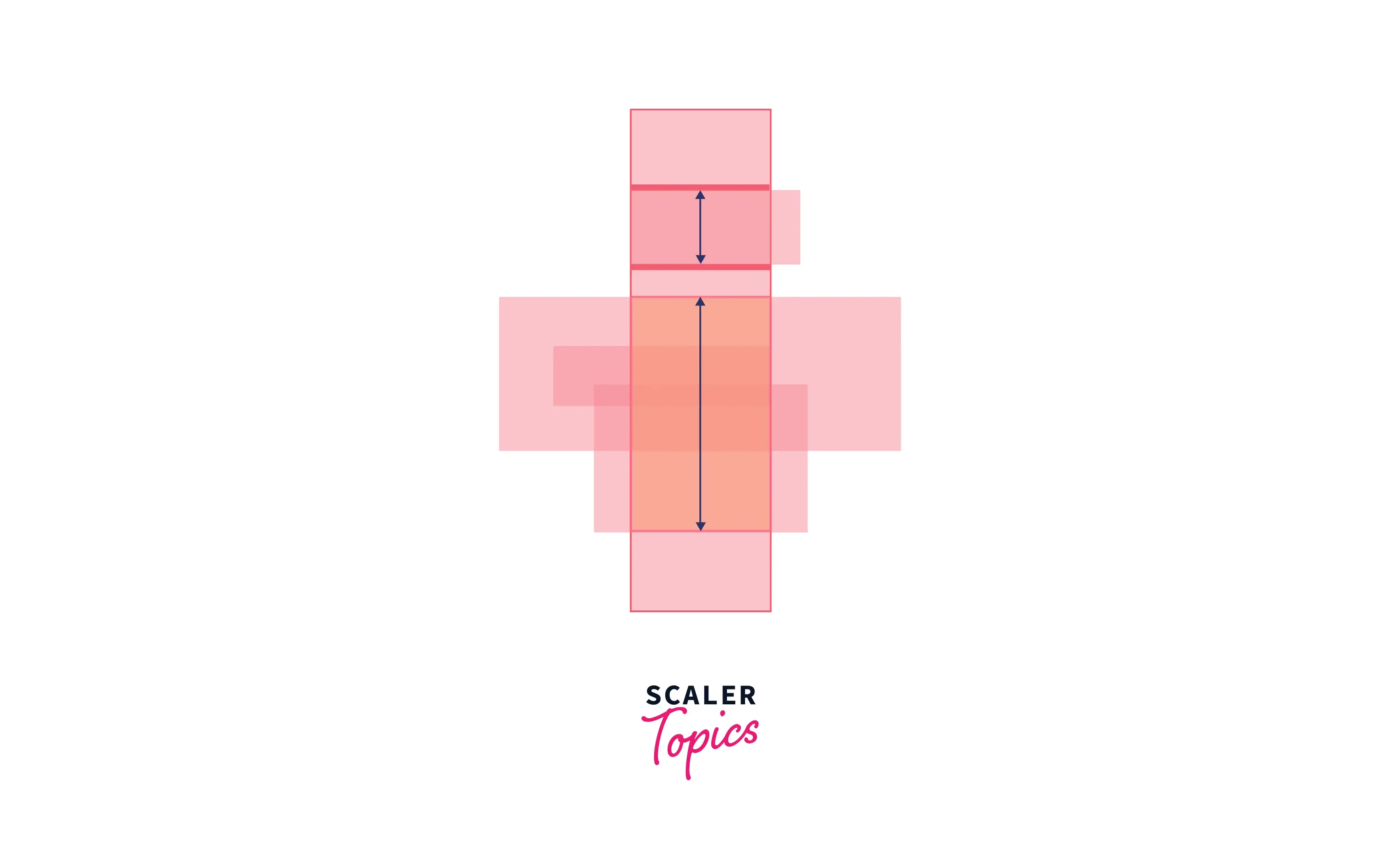
These images portray the horizontal sweep from the bottom up. This procedure is carried on for all events of the vertical sweep line. Hence in this algorithm, we are making use of 2 sweep lines.
Convex Hull
By now, surely you have understood the sweep line technique. Let's move on to another problem -
You are given a set of points S, and your task is to find the convex hull i.e. the smallest polygon that covers all the points in set S.
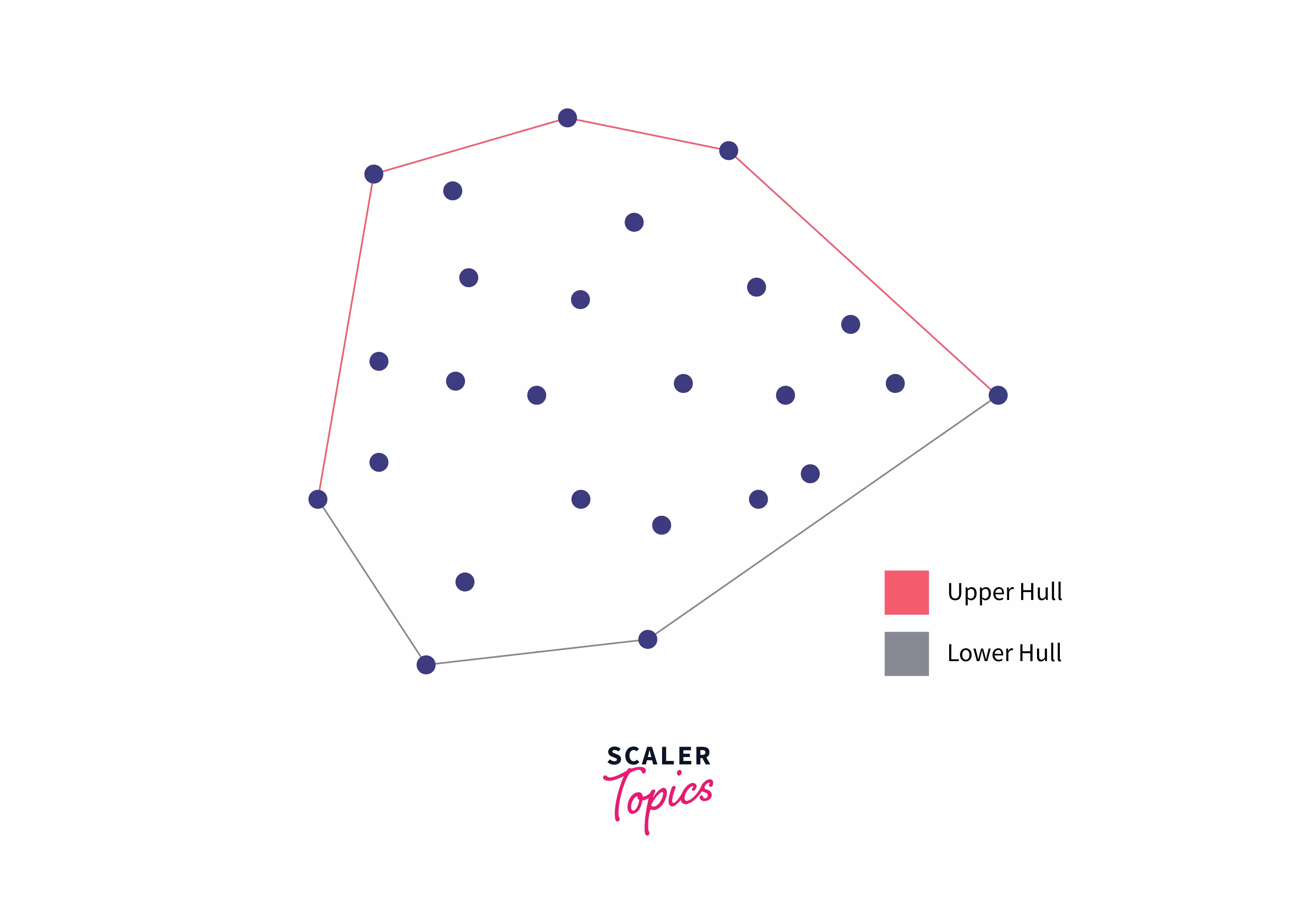
Here in the image, you can see that we have a set of points and the polygon, created by the red and grey connections between dots is the smallest convex (outward) polygon that covers all the other points of the set S.
We have two algorithms to solve this problem --- the algorithm - Graham scan which requires us to sort by angle, and Andrew's algorithm.
We're going to discuss the Andrew algorithm, which works by splitting the convex hull, into 2 parts - the lower and the upper hull as you can also see in the diagram above. These two hulls usually meet at the ends however, if by any chance there is more than one point that has a minimal or the maximal X coordinate then those are joined with the help of a vertical line segment.
Let's talk about first building the upper hull. For this, we will have to start with the minimum X coordinate and break any ties that might exist by taking the point with the larger Y coordinate. Next, points are added in the order of increasing the X coordinate, while always taking the largest Y coordinate value if multiple points have the same X value. With this procedure, it might also happen that the hull becomes concave (inwards) instead of convex.
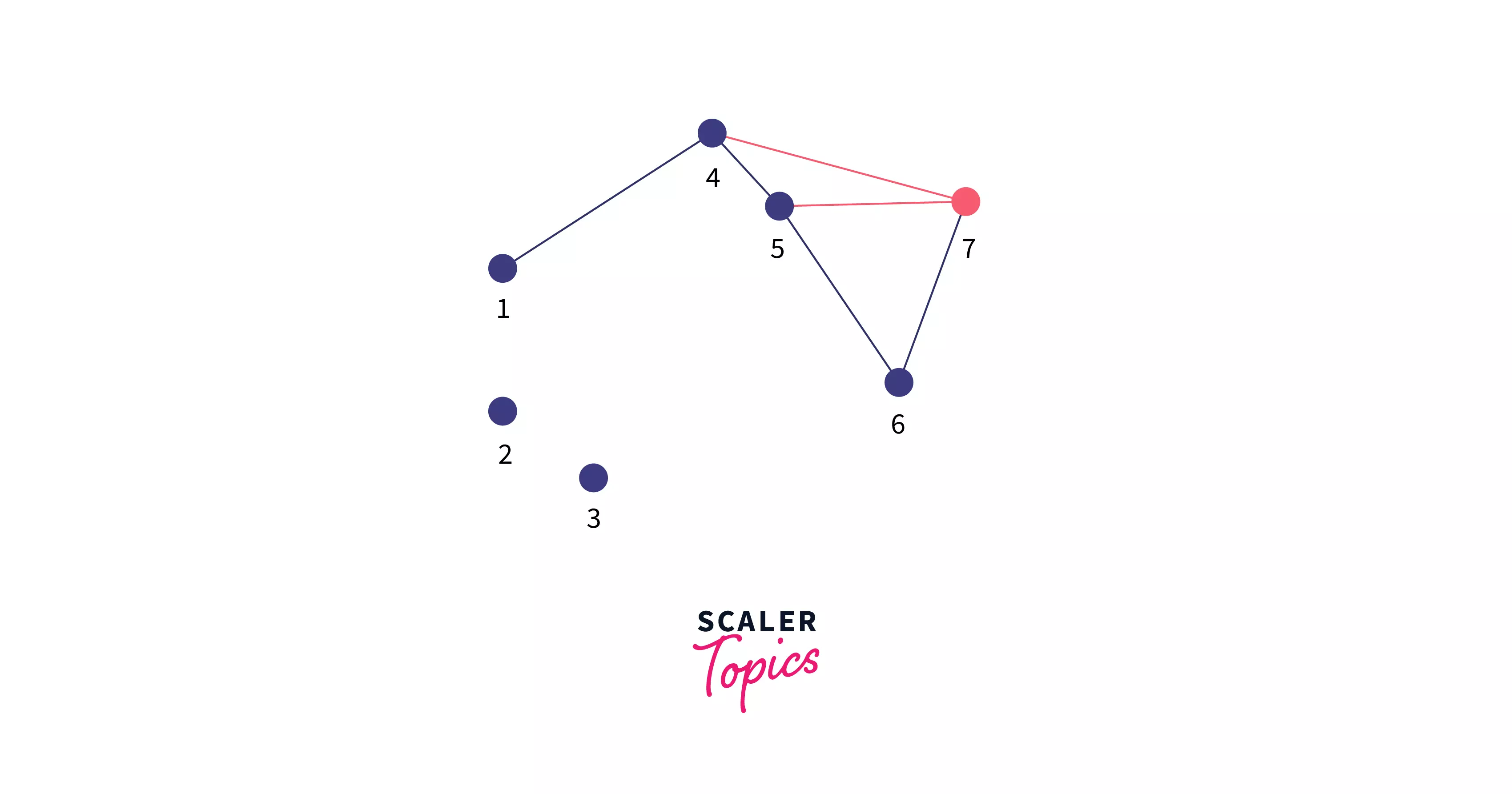
For example, in this set of points, using the procedure given above, we would select points in this order: 1 -> 4 -> 5 -> 6 -> 7, thus making our hull concave (black lines), however, we want a convex hull (red lines).
After we have added point 7 to the hull, to confirm that the hull formed is convex, we check if the last triangle (using the last 3 points) is convex. In this case, we can see that using the points 5, 6, and 7, the triangle formed is not convex, and hence we would delete the second last point i.e. 6. We repeat this process till the last 3 points form a convex triangle. Upon the removal of 6, you can see that the last 3 points - 4, 5, 7 also do not give us a convex triangle, and we remove the second last point i.e. 5. The remaining points are now 1, 4, and 7 and this gives us a convex triangle.
The same procedure is followed to create the lower hull, wherein we take points in increasing order of X and decreasing order of Y and removing the concave triangles till the last 3 points form a convex triangle.
We would then remove the last point in each list of points of the upper and lower hulls since it would be the same and then concatenate the lists to find the convex hull.
The complexity of this algorithm is again O(NlogN) due to sorting, which is the same as other algorithms we discussed that made use of the line sweep algorithm.
Manhattan Minimum Spanning Tree (MST)
Coming to the final algorithm that uses the line sweep technique. In this problem, we're going to combine the line sweep algorithm with the divide and conquer algorithm. This problem is finding the minimum spanning tree of a set of points, and the distance between any two points is the Manhattan distance. You can read more about the minimum spanning tree on Google.
Let's break this problem into simpler problems. We have standard algorithms that work on graphs such as Prim's algorithm which finds the MST in O((E + N)log N) for a total of E edges. And so here's how we're going to solve it, for every point P, we will consider only its nearest neighbors in the 8 octants of the plane. Take a look at the figure below to understand better.
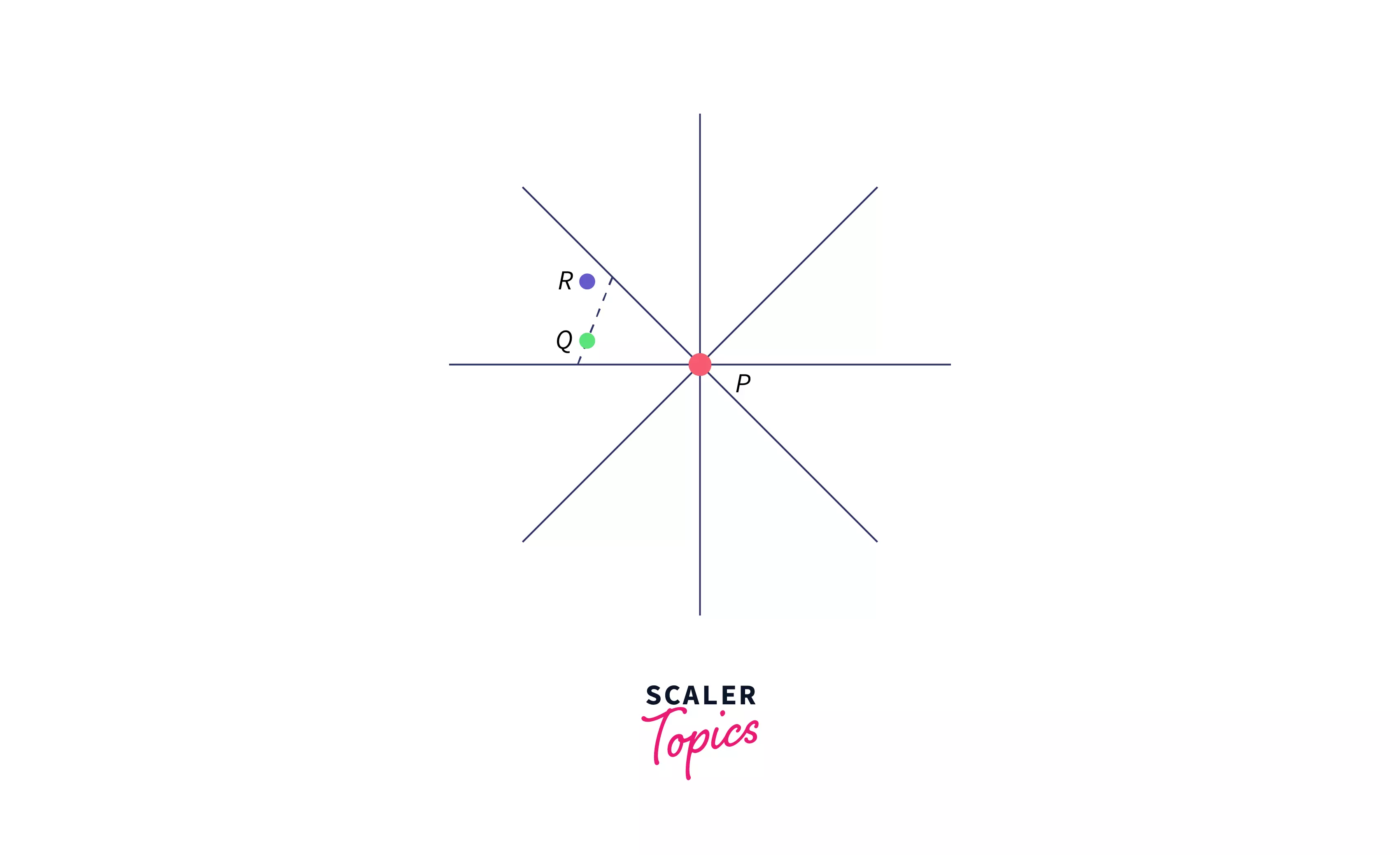
We have a point P and its 8 octants are marked with lines. In the west-north-west octant, we have the points Q and R with Q being the closest to P. The dashed line indicates all the points that would lie on that line would have the same Manhattan distance as Q from P. R is some other point in that octant. Let's say that PR is an edge in our spanning tree, then it can be removed and replaced, by either QR or PQ to generate a better-spanning tree since this shape of our octant gives us the guarantee that the two values |QR| and |PR| are equal. Hence we would not need to consider the edge PR while creating our minimum spanning tree.
So now our problem has been reduced to finding the nearest neighbor of P in each octant. For this example, we will only consider the octant shown in the figure, as all the other octants would be handled the same way. To find the nearest neighbor in this octant is the same as finding the point (x, y) that has the largest value of (x - y), that is subject to an upper bound on (x + y), and it's lower bound would be on y. This is the form in which we can work on this problem.
Before we move ahead, imagine for a while, that there is no lower bound on y. If this was the case, we could have solved this problem in a slightly easy manner. Here's where the sweep line would come into play: We would sweep the line through all the points in the increasing order of (x + y), with Q being the point that has the largest value of (x - y).
Now, another technique comes into play - the divide and conquer. We will create 2 halves and create a partition using the help of a horizontal line and then recursively solve the problem for each half. For the upper half of point P, we know that Q is the closest point to P. For the bottom half, we must ignore the upper half and find the closest point. However we can also take these points together, here's how: sweep through all the points in increasing value of (x + y) while still keeping a track of the point that is the best (the best point has the largest value of (x - y). So for every point in the bottom partition, we check whether this "best" point is better than the current neighbor.
So far, the assumptions were that all these points can easily be partitioned on the Y-axis and can also be swept over in the increasing value of x + y. This category of problems that make use of divide and conquer as well as the line sweep technique, have a similar structure to the sorting algorithm - merge sort.
Conclusion
- The line sweep algorithm is a technique that uses the idea of making use of a vertical imaginary line. This line moves in the rightward direction upon the occurrences of certain events that are defined by the current problem at hand.
- Some of the problems that can be solved using the line sweep algorithm are:
- Closest Pair:
- You are given a set of points, and you must find the pair of points that are closest to each other.
- Line Segment Intersections:
- The task is to find all the intersections of horizontal and vertical lines.
- Union of Rectangles:
- You are given a set of N axis-aligned rectangles, i.e. the edges of rectangles are parallel to either the X-axis or the Y-axis. You are required to find the area of the union of all these rectangles.
- Convex Hull:
- You are given a set of points S, and your task is to find the convex hull i.e. the smallest polygon that covers all the points in set S.
- Manhattan Minimum Spanning Tree:
- Find the minimum spanning tree of a set of points, and the distance between any two points is the Manhattan distance.
- Closest Pair:
- All of these algorithms use(an) imaginary line(s) that are swept across the plane to process the points and find the solution to the problem.
