Manacher's Algorithm

Brute Force Approach

The brute force / naive approach is slower than Manacher's algorithm, but it is a good stepping stone for understanding the problem and Manacher's algorithm. The Brute force approach is to check each substring of the given string whether the substring is a palindrome or not.

To implement the brute force approach, first, we will use a nested loop to get each substring, and then nest another loop to check whether that substring is a palindrome or not.

Implementation in C++ 17

Implementation in Python 3

Implementation in Java 8

The output is the same for all of these (the implementation is the same, the difference is only of the programming languages).

Output

In the above examples, we are using the brute force approach to find the longest palindromic substring in the given string.
The printSubstring() function is used for printing a substring, longestPalSubstring() is used to print the longest palindromic substring.

Time Complexity:

$O(N^{3})$

In the brute force approach, three nested loops are used to find the longest palindromic substring, so the time complexity will be $O(N^{3})$.

Space Complexity

$O(1)$

No extra space is needed in this approach, so the space complexity will be $O(1)$.

Manacher’s algorithm

Manacher's algorithm is used to find the longest palindromic substring in any given string. This algorithm is faster than the brute force approach, as it exploits the idea of a palindrome happening inside another palindrome.

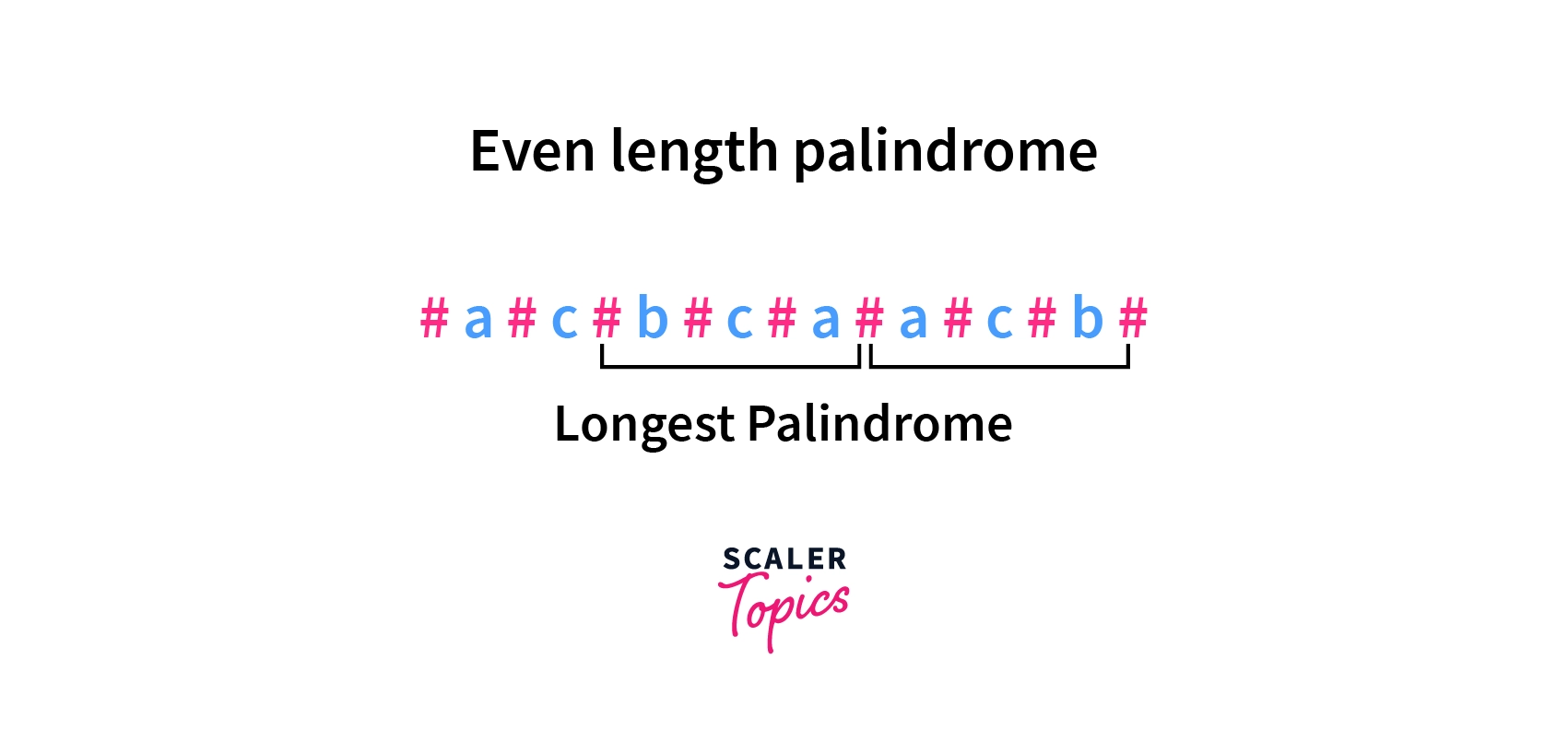
Manacher's algorithm is designed to find the palindromic substrings with odd lengths only. To use it for even lengths also, we tweak the input string by inserting the character "#" at the beginning and each alternate position after that (changing "abcaac" to "#a#b#c#a#a#c#").

In the case of an odd length palindrome, the middle character will be a character of the original string, surrounded by "#". In the case of an even length palindrome, the middle character will be a "#" character. Now we will learn each of its steps for a deeper understanding, which will help us in its implementation.

Steps of the Manacher's Algorithm

Steps of the Manacher's algorithm are as follows:

1. Create an array or a list ($sChars$) of length $strLen$ which is $2 * n + 3$ ($n$ being the length of the given string), to modify the given string.
2. Assign the first and last element of $sChars$ to be "@" and "$", respectively.
3. Fill the blank spaces in $sChars$ by characters of the given string and "#" alternatively.
4. Declare variables
   • Implicating maximum detected length of palindrome substring $maxLen = 0$
   • Position from where to start searching $start = 0$
   • Highest position of the extreme right character of all detected palindromes $maxRight = 0$
   • Center of the detected palindrome $center = 0$.
5. Create an array or a list $p$ to record the width of each palindrome about their center, center being the corresponding characters in $sChars$.
6. Create a for loop iterating from $1$ to $strLen - 1$, with $i$ incrementing in each iteration.
7. In each iteration, check if $i < maxRight$, if yes, then assign minimum of $maxRight - i$ and $p[2 * center - i]$ to $p[i]$.
8. Nest a while loop inside the for loop, to count with width along the center, condition being, $sChars[i + p[i] + 1]$ is equal to $sChars[i - p[i] - 1]$, if yes, increment $p[i]$ by 1.
9. To update center, check if $i + p[i]$ is greater than $maxRight$, if yes, assign $center$ to be $1$, and $maxRight$ to be $i + p[i]$.
10. For updating the Maximum length detected, check if $p[i]$ is greater than $maxLen$, if yes, then assign $start$ to be $(i - p[i] - 1) / 2$, and $maxLen$ to be $p[i]$.
11. Come out of the for loop, and print the substring in the given string, starting from $start$ and ending at $start + maxLen - 1$.

Implementation of Manacher's Algorithm

Now we will implement Manacher's algorithm in C++17, Java 8, and Python 3

Things to Note:

• $strLen$ is the length of the modified (after inserting extra characters) list/array.
• $sChars$ is the modified (after inserting extra characters) list/array.
• $maxLen$ is the length of the longest palindrome detected.
• $start$ is the position from which we have to search for a palindrome.
• $maxRight$ is the position of the rightmost character of a palindrome.
• $center$ is the center of a palindrome
• $p$ is the list/array of the width of palindromes about their center, center being the corresponding characters in $sChars$.

Implementation in C++ 17

Implementation in Python 3

Implementation in Java 8

The output is the same for all of these (the implementation is the same, the difference is only of the programming languages).

Output

In the above examples, we are using the Manacher’s algorithm to find the longest palindromic substring in the given string.
The printSubstring() function is used for printing a substring, longestPalSubstring() is used to print the longest palindromic substring.

Complexity Analysis of Manacher’s Algorithm

Analysing the Time and Spatial complexity of Manacher's algorithm ($N$ here is the number of characters inside the given string):

Time Complexity:

$O(N)$

At the first glance, it may seem that the algorithm has a $O(N^2)$ time complexity due to nested loops, but that's not the case, a more careful analysis shows that the algorithm is linear and amortized.

Each successful comparison results in $maxRight$ moving one step forward, and it never reduces, therefore, the inner while loop gets executed at most $n$ times. Hence, the time complexity of Manacher's algorithm will be $O(N).$

Space Complexity:

$O(N)$

We need $O(n)$ space to create and form $p$ (palindrome width).

Boost Your Tech Profile! Join Our DSA Courses for Advanced Algorithmic Mastery. Enroll Now to Stand Out in the Coding Landscape!