September 26, 2024

Primality Test

The Primality test is an algorithm for determining whether a given positive integer is a prime number or not.There are many methods to check whether a number is prime or not, like, the School Method, Trial Division Method, Fermat Primality test, and Miller-Rabin Primality test.

Scope of the Article

In this article we will discuss different primality tests in data structures.
All the primality tests are explained using steps and pseudocode in this article.
The complexity analysis of each method will also be discussed in this article.
The programs are implemented in C++, Java, and Python in this article.

Takeaways

Algorithm for determining whether a given positive integer is a prime number or not :

School method
Trial Division Method
Fermat Primality Test
Miller-Rabin Primality Test

What is Primality Test?

The Primality test is an algorithm for determining whether a given positive integer is a prime number or not.

The primality of a number can also be checked by determining whether it is a composite number or not, because if the number is not a composite number nor 1, then it must be a prime number.

Example

Source Code – C++17

// Determining whether a number is a prime or not

# include<iostream>
using namespace std;

// Function for Primality test
bool isPrime(int n){

    // Corner Case
    if (n<=1)
        return false;

    // Checking from 2 to n-1
    for (int i=2; i<n; i++)
        if (n % i == 0)
            return false;

    return true;
}

// Driver code
int main(){
    int x = 3;
    isPrime(x) ? cout<<x<<" is a prime number.\n": cout<<x<<" is not a prime number.\n";

    int y = 12;
    isPrime(y) ? cout<<y<<" is a prime number.\n": cout<<y<<" is not a prime number.\n";
}

Source Code – Java (1.8)

// Determining whether a number is a prime or not

class PrimeCheck{

    // Function for Primality test
    static boolean isPrime(int n){

        // Corner Case
        if (n<=1)
            return false;

        // Checking from 2 to n-1
        for (int i=2; i<n; i++)
            if (n % i == 0)
                return false;

        return true;
    }

    // Driver code
    public static void main(String args[]){
        int x = 3;
        System.out.println(isPrime(x) ? (x + " is a prime number."): (x + " is not a prime number."));

        int y = 12;
        System.out.println(isPrime(y) ? (y + " is a prime number."): (y + " is not a prime number.")); 
    }
}

Source Code – Python 3

# Determining whether a number is a prime or not

# Function for Primality test
def isPrime(n):

    # Corner case
    if n <= 1: 
        return False

    # Checking from 2 to n-1
    for i in range(2, n):
        if n % i == 0:
            return False

    return True

# Driver code
x = 3
print(x, "is a prime number.") if isPrime(x) else print(x, "is not a prime number.")

y = 12
print(y, "is a prime number.") if isPrime(y) else print(y, "is not a prime number.")

The output is the same for all of the implementations as they peform the same thing, the only difference being the programming language.

Output

3 is a prime number.
12 is not a prime number.

In the above examples, we are checking whether the given number is a prime number or not, to do so, we are iterating from $2$ to $n - 1$ to check if these numbers divide the given number. If they do, then the given number is not a prime number, else it is a prime number.

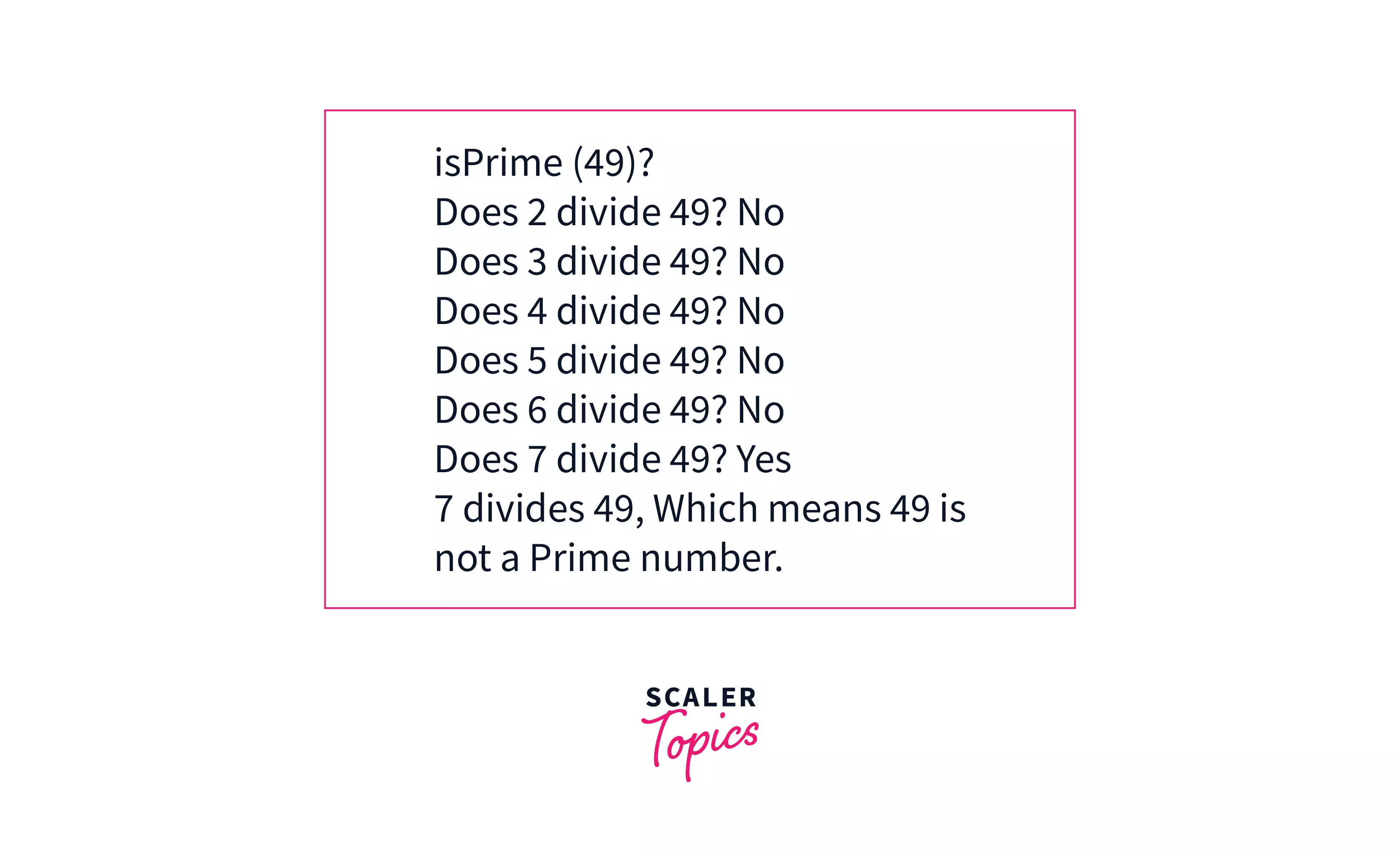
School method

The school method is a simple solution that comes first to everyone’s mind for primality check as it is the simplest of all.

In the School Method algorithm, we iterate through all the numbers from $2$ to $n - 1$ (the number to be checked is $n$ ) and check if they divide the number $n$ .

Complexity Analysis

Time Complexity: $O (N)$

The time complexity of the School Method primality check is $O (N)$ as we iterate $N - 2$ times.

Space Complexity: $O (1)$

The space complexity here is constant.

The algorithm in the example above is School Method only.

Optimized School Method

In the School Method, we can do some optimizations like:

Instead of checking till $n$ , we will check till $\sqrt{n}$ because a factor of $n$ larger than $\sqrt{n}$ must be a multiple of a number smaller than $\sqrt{n}$ that has been already checked and should not be checked again.
We will first check the divisibility of $n$ by $2$ and $3$ , then check its divisibility by numbers of the form $6 k - 1$ and $6 k + 1$ starting at $k = 1$ . We do so because any integer greater than $4$ can be expressed in the form of $6 k - 1$ , $6 k$ , $6 k + 1$ , $6 k + 2$ , $6 k + 3$ , and $6 k + 4$ (for $k > 0$ ), but integers of the form $6 k$ , $6 k + 2$ , $6 k + 3$ , and $6 k + 4$ will be divisible by $2$ or $3$ .

Let’s have a look at its implementation in the section below.

Implementation of the Optimized School Method

Source Code – C++17

// Determining whether a number is a prime or not

# include<iostream>
# include<math.h>
using namespace std;

// Function for Primality test
bool isPrime(int n){

    // Corner Cases
    if (n<=3)
        return n>1;
    else if (n%2==0 || n%3==0)
        return false;

    // Checking through numbers of the form 6k-1 and 6k+1 (k>0)
    for (int i=5; i<sqrt(n); i+=6)
        if ((n % i == 0) || (n%(i+2)==0))
            return false;

    return true;
}

// Driver code
int main(){
    int x = 3;
    isPrime(x) ? cout<<x<<" is a prime number.\n": cout<<x<<" is not a prime number.\n";

    int y = 12;
    isPrime(y) ? cout<<y<<" is a prime number.\n": cout<<y<<" is not a prime number.\n";
}

Source Code – Java (1.8)

// Determining whether a number is a prime or not
import java.lang.Math;

class PrimeCheck{

    // Function for Primality test
    static boolean isPrime(int n){

        // Corner Cases
        if (n<=3)
            return n>1;
        else if (n%2==0 || n%3==0)
            return false;

        // Checking through numbers of the form 6k-1 and 6k+1 (k>0)
        for (int i=5; i<Math.sqrt(n); i+=6)
            if ((n % i == 0) || (n % (i+2) == 0))
                return false;

        return true;
    }

    // Driver code
    public static void main(String args[]){
        int x = 3;
        System.out.println(isPrime(x) ? (x + " is a prime number."): (x + " is not a prime number."));

        int y = 12;
        System.out.println(isPrime(y) ? (y + " is a prime number."): (y + " is not a prime number.")); 
    }
}

Source Code – Python 3

# Determining whether a number is a prime or not
import math

# Function for Primality test
def isPrime(n):

    # Corner cases
    if n <= 3: 
        return n>1
    elif n % 2 == 0 or n % 3 == 0:
        return False

    # Checking through numbers of the form 6k-1 and 6k+1 (k>0)
    for i in range(5, int(math.sqrt(n)), 6):
        if n % i == 0 or n % (i + 2) == 0:
            return False

    return True

# Driver code
x = 3
print(x, "is a prime number.") if isPrime(x) else print(x, "is not a prime number.")

y = 12
print(y, "is a prime number.") if isPrime(y) else print(y, "is not a prime number.")

The output is the same for all of the implementations as they peform the same thing, the only difference being the programming language.

Output

3 is a prime number.
12 is not a prime number.

In the above examples, we are checking whether the given number is a prime number or not, to do so, we are first checking its divisibility by $2$ and $3$ , then checking its divisibility by numbers of the form $6 k - 1$ and $6 k + 1$ . If the given number is divisible by any number then it is not a prime number, else it is.

Complexity Analysis

Time complexity: $O (\sqrt{N})$

The asymptotic time complexity of the Optimized School Method primality check is $O (\sqrt{N})$ because we iterate $\sqrt{N} / 6$ ( $i + = 6$ in the for loop) times in this algorithm.

Space Complexity: $O (1)$

The space complexity here is constant.

Trial Division Method

The Trial Division Method is a primality check algorithm in which we accept some integer $n$ , check if any number from 2 to $\sqrt{n}$ divides the given integer, if a divisor is found then $n$ is a composite number, otherwise, it is a prime number. It is very similar to the school method.

Complexity Analysis

Time complexity: $O (\sqrt{N})$

The time complexity of The Trial Division primality check is $O (\sqrt{N})$ as we iterate $\sqrt{N} - 1$ times.

Space Complexity: $O (1)$

The space complexity here is constant.

Fermat Primality Test

The Fermat Primality test is a probabilistic method to determine whether the given integer is a probable prime number or not.

It is based on Fermat's Little Theorem that states if $p$ is a prime number and $a$ is not divisible by $p$ , then $a^{p - 1} \equiv 1 (m o d p)$ , i.e $a^{p - 1} = k * p + 1$ (where $k$ is an integer constant).

If we want to test $p$ for a prime number, then we will pick some random integers $a$ that are not divisible by $p$ and see whether the congruency holds or not. If the congruency doesn’t hold for a value of $a$ , then it will be a proof that $p$ is a composite number, but if the congruency holds for more than one values of $a$ , then $p$ is a probable prime number.

Algorithm Steps

Repeat the following $k$ times (higher value of $k$ indicates higher probability of correct results):
- Handle corner cases for $p < 3$ ( $p$ is the number to be tested).
- Pick a random number $a$ in the range $1 < a < p$ .
- If $a^{p - 1} ≢ 1 (m o d p)$ , then return $F a l s e$ .
Return $T r u e$ , $p$ is probably a prime number.

Example

Let us assume, we have to check whether $n = 221$ is a prime number or not. We will randomly pick a number $a$ in the range $1 < a < 221$ . Then we will check whether the congruency holds or not.

For $a = 38$ ,

$38^{221 - 1} \equiv 1 (m o d 221)$ , as $a^{p - 1} \equiv 1 (m o d p)$
$=> 38^{220} \equiv 1 (m o d 221)$ ,

Now there can be two cases, $221$ is a prime number, or $38$ is a Fermat liar. To proceed, let’s take $a = 24$ .

but, $24^{220} ≢ 1 (m o d 221)$ , as $24^{220} \equiv 81 (m o d 221)$ .

This proves that $221$ is a composite number and $38$ is Fermat liar, $24$ being the Fermat witness for the compositeness of $221$ .

Complexity Analysis

`Time Complexity`: $O (K * l o g (N))$

Here, $K$ is the number of iterations, and $N$ is the number to be tested for primality. $l o g (N)$ is the time complexity for computing $a^{p - 1}$ and the algorithm is repeated $K$ times. So the time complexity is $O (K * l o g (N))$ .

`Space Complexity`: $O (1)$

There is no need for extra space, so the space complexity is constant.

The Fermat’s little theorem is used for one more Primality test, called the Miller-Rabin Primality Test.

Miller-Rabin Primality Test

The Miller-Rabin Primality Test is also a probabilistic method to determine whether the given integer is a prime number or not, similar to the Fermat Primality Test. It is also based on the Fermat’s Little Theorem (discussed in the above section).

This test was discovered by Gary Lee Miller in 1976, later modified by Michael Oser Rabin in 1980.

The result of this test will be whether the given number is a composite number or a probable prime number. The probable prime numbers in the Miller-Rabin Primality Test are called strong probable numbers, as they have a higher chance of being a prime number than in the Fermat's Primality Test.

A number $n$ is said to be strong probable prime number to base $a$ if one of these congruence relations (equivalence relations in modulo arithmetics, $A \equiv B (m o d C)$ means $A$ is congruent to $B$ modulo $C$ ) holds:

$a^{d} \equiv 1 (m o d n)$
$a^{2^{r} * d} \equiv - 1 (m o d n)$

Algorithm Steps

$n$ is the number to be tested.

$k$ indicates the accuracy of the test.

$d$ is an odd number such that $n - 1$ can be written in the form of $d * 2^{r}$ (Since $n$ is odd, $n - 1$ must be even and $r > 0$ ).

$i s P r i m e (i n t n, i n t k)$

Handle base cases for $n < 3$ .
if $n$ is even, return $F a l s e$ .
Find an odd number $d$ .
Loop the following $k$ times:
- Check if $m i l l e r T e s t (n, d) == f a l s e$ , if yes, return $F a l s e$ .
Return $T r u e$ .

$m i l l e r R a b i n T e s t (i n t n, i n t d)$

Pick a random number $a$ in the range $2 \leq a \leq n - 2$ .
Compute $x = p o w (a, d)$ .
Return $T r u e$ if $x == 1 o r x == n - 1$ .
Loop the following till $d == n - 1$ .
- $x = (x * x) % n$ .
- Return $F a l s e$ if $x == 1$ .
- Return $T r u e$ if $x == n - 1$ .

Implementation of the `Miller-Rabin Primality Test`

Source Code – C++17

// Determining whether a number is a prime or not

# include<iostream>
# include<math.h>
using namespace std;

// Function for modular exponentiation. It returns (x^y) % p
int pow(int x, unsigned int y, int p){
    int res = 1;

    // Update x if it is more than or equal to p
    x = x % p; 

    while (y > 0)
    {
        // If y is odd, multiply x with result
        if (y & 1)
            res = (res*x) % p;

        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}

// This function is called for all k trials.
bool millerRabinTest(int d, int n){

    // Pick a random number in [2,n-2]
    // n > 4, because of the corner cases
    int a = 2 + rand() % (n - 4);

    // Computing a^d % n
    int x = pow(a, d, n);

    if (x == 1  || x == n-1)
       return true;

    // Keep squaring x till:
    // (i)  (x^2) % n is not 1
    // (ii) (x^2) % n is not n-1
    while (d != n-1){
        x = (x * x) % n;
        d *= 2;

        if (x == 1)      return false;
        if (x == n-1)    return true;
    }

    // Return composite
    return false;
}

// Function for Primality test
bool isPrime(int n, int k){

    // Corner Cases
    if (n<=3)
        return n>1;
    else if (n==4)
        return false;

    // Finding r such that n = 2^d * r + 1, (r > 0)
    int d = n - 1;
    while (d % 2 == 0)
        d /= 2;

    // Iterating k times
    for (int i = 0; i < k; i++)
         if (!millerRabinTest(d, n))
              return false;

    return true;
}

// Driver code
int main(){
    int k = 10;

    int x = 3;
    isPrime(x, k) ? cout<<x<<" is probably a prime number.\n": cout<<x<<" is a composite number.\n";

    int y = 12;
    isPrime(y, k) ? cout<<y<<" is probably a prime number.\n": cout<<y<<" is a composite number.\n";

    int z = 541;
    isPrime(z, k) ? cout<<z<<" is probably a prime number.\n": cout<<z<<" is a composite number.\n";

}

Source Code – Java (1.8)

// Determining whether a number is a prime or not
import java.math.*;

class PrimeCheck{

    // Function for modular exponentiation. It returns (x^y) % p
    static int power(int x, int y, int p) {

        int res = 1;

        // Update x if it is more than or equal to p
        x = x % p;

        while (y > 0) {
            // If y is odd, multiply x with result
            if ((y & 1) == 1)
                res = (res * x) % p;

            // y must be even now
            y = y >> 1; // y = y/2
            x = (x * x) % p;
        }
        return res;
    }

    // This function is called for all k trials.
    static boolean millerRabinTest(int d, int n) {

        // Pick a random number in [2,n-2]
        // n > 4, because of the corner cases
        int a = 2 + (int)(Math.random() % (n - 4));

        // Computing a^d % n
        int x = power(a, d, n);

        if (x == 1 || x == n - 1)
            return true;

        // Keep squaring x till:
        // (i) (x^2) % n is not 1
        // (ii) (x^2) % n is not n-1
        while (d != n - 1) {
            x = (x * x) % n;
            d *= 2;

            if (x == 1)
                return false;
            if (x == n - 1)
                return true;
        }

        // Return composite
        return false;
    }

    // Function for Primality test (returns True if the given number is probably prime and False if it is a composite.)
    static boolean isPrime(int n, int k){

        // Corner Cases
        if (n<=3)
            return n>1;
        else if (n==4)
            return false;

        // Finding r such that n = 2^d * r + 1, (r > 0)
        int d = n - 1;

        while (d % 2 == 0)
            d /= 2;

        // Iterating k times
        for (int i = 0; i < k; i++)
            if (!millerRabinTest(d, n))
                return false;

        return true;
    }

    // Driver code
    public static void main(String args[]){
        int k = 10;

        int x = 3;
        System.out.println(isPrime(x, k) ? (x + " is probably a prime number."): (x + " is a composite number."));

        int y = 12;
        System.out.println(isPrime(y, k) ? (y + " is probably a prime number."): (y + " is a composite number.")); 

        int z = 541;
        System.out.println(isPrime(z, k) ? (z + " is probably a prime number."): (z + " is a composite number."));
    }
}

Source Code – Python 3

# Determining whether a number is a prime or not
import random

# This function is called for all k trials.
def millerRabinTest(d, n):

    # Pick a random number in [2,n-2]
    # n > 4, because of the corner cases
    a = 2 + random.randint(1, n - 4);

    # Compute a^d % n
    x = a**d%n

    if (x == 1 or x == n - 1):
        return True;

    # Keep squaring x till:
    # (i)  (x^2) % n is not 1
    # (ii) (x^2) % n is not n-1
    while (d != n - 1):
        x = (x * x) % n;
        d *= 2;

        if (x == 1):
            return False;
        if (x == n - 1):
            return True;

    # Return composite
    return False;

# Function for Primality test (returns True if the given number is probably prime and False if it is a composite.)
def isPrime(n, k):

    # Corner cases
    if n <= 3: 
        return n>1
    elif n==4:
        return False

    # Finding r such that n = 2^d * r + 1, (r > 0)
    d = n - 1;
    while d % 2 == 0:
        d //= 2;

    # Iterating k times
    for i in range(k):
        if (millerRabinTest(d, n) == False):
            return False;

    return True;


# Driver code
k = 10

x = 3
print(x, "is probably a prime number.") if isPrime(x, k) else print(x, "is a composite number.")

y = 12
print(y, "is probably a prime number.") if isPrime(y, k) else print(y, "is a composite number.")

z = 541
print(z, "is probably a prime number.") if isPrime(z, k) else print(z, "is a composite number.")

The output is the same for all of the implementations as they peform the same thing, the only difference being the programming language.

Output

3 is probably a prime number.
12 is a composite number.
541 is probably a prime number.

In the above examples, we are checking whether the given number is a probable prime number or a composite number, to do so, we are using the Miller-Rabin Primality Test. If the function returns $T r u e$ , then the given number is a probable prime number, otherwise, it is a composite number.

The Miller-Rabin Test, being an extension of the Fermat’s Primality Test, is more accurate than Fermat’s Primality Test, thus, it is preferred over that.

Complexity Analysis

Time Complexity: $O (K * l o g^{3} (N)$

The time complexity of the Miller-Rabin Primality Test is $O (K * l o g^{3} (N)$ , where $N$ is the number to be checked for primality, and $K$ is the number of iterations performed for accuracy as per the requirement.

Space Complexity: $O (1)$

There is no need for extra space, so the space complexity is constant.

Conclusion

Primality tests are used to determine whether a given number is a prime or not.
The School method is a naive algorithm of $O (N)$ time complexity.
The Optimized School method and the Trial Division algorithm have a time complexity of $O (\sqrt{n})$ .
The Fermat's Primality test and Miller-Rabin Primality test return whether a number is composite or a probable prime, and are based on Fermat’s Little Theorem.
The time complexity of the Fermat's Primality Theorem is $O (K * l o g (N))$ .
The time complexity of the Miller-Rabin Primality Test is $O (K * l o g^{3} (N)$ .

Author

Ayush Kumar

View all posts

Primality Test

Scope of the Article

Takeaways

What is Primality Test?

Example

School method

Complexity Analysis

Time Complexity: $O (N)$

Space Complexity: $O (1)$

Optimized School Method

Implementation of the Optimized School Method

Complexity Analysis

Time complexity: $O (\sqrt{N})$

Space Complexity: $O (1)$

Trial Division Method

Complexity Analysis

Time complexity: $O (\sqrt{N})$

Space Complexity: $O (1)$

Fermat Primality Test

Algorithm Steps

Example

Complexity Analysis

`Time Complexity`: $O (K * l o g (N))$

`Space Complexity`: $O (1)$

Miller-Rabin Primality Test

Algorithm Steps

Implementation of the `Miller-Rabin Primality Test`

Complexity Analysis

Time Complexity: $O (K * l o g^{3} (N)$

Space Complexity: $O (1)$

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Primality Test

Scope of the Article

Takeaways

What is Primality Test?

Example

School method

Complexity Analysis

Time Complexity: O(N)

Space Complexity: O(1)

Optimized School Method

Implementation of the Optimized School Method

Complexity Analysis

Time complexity: O(N)

Space Complexity: O(1)

Trial Division Method

Complexity Analysis

Time complexity: O(N)

Space Complexity: O(1)

Fermat Primality Test

Algorithm Steps

Example

Complexity Analysis

Time Complexity: O(K∗log(N))

Space Complexity: O(1)

Miller-Rabin Primality Test

Algorithm Steps

Implementation of the Miller-Rabin Primality Test

Complexity Analysis

Time Complexity: O(K∗log3(N)

Space Complexity: O(1)

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Featured articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Time Complexity: $O (N)$

Space Complexity: $O (1)$

Time complexity: $O (\sqrt{N})$

Space Complexity: $O (1)$

Time complexity: $O (\sqrt{N})$

Space Complexity: $O (1)$

`Time Complexity`: $O (K * l o g (N))$

`Space Complexity`: $O (1)$

Implementation of the `Miller-Rabin Primality Test`

Time Complexity: $O (K * l o g^{3} (N)$

Space Complexity: $O (1)$