Segment Tree with Lazy Propagation

Abstract
A Segment Tree is an efficient and flexible data structure that is used to solve range queries while handling updates at the same time. The lazy Propagation technique is used in a segment tree to solve range queries in O(log n) time complexity. In lazy propagation, we make copy nodes for each node in the Segment Tree and use these copy nodes to store the updates. Lazy Propagation is a technique where we postpone the updates for the future and use them only when these updates are required.
Introduction
As discussed above a segment tree is a highly versatile and efficient data structure used to solve problems involving range queries and is flexible enough to handle update queries over a range as well as point update queries in O(log n) time complexity. We would recommend everyone to refer to the article Segment Tree, as a prerequisite to this article where we discussed how we can use a Segment Tree to handle point updates. In this post, we will see how we can use a Segment Tree to handle range update queries.
Let's consider that you have an array as follows, array= [2,5,4,3]. Now you need to solve range minimum queries or the minimum in a given range for the given array while handling range updates at the same time. Now if we need to modify only a single element in the array we can do it using a simple Segment Tree. However, if we need to update an entire range in the update query. Say, we need to increase every element of the array in the range [1,3] (1 based indexing) by 5. Then we will not be able to use a simple Segment tree to solve the above problem efficiently. We will see why in the latter part of this article.
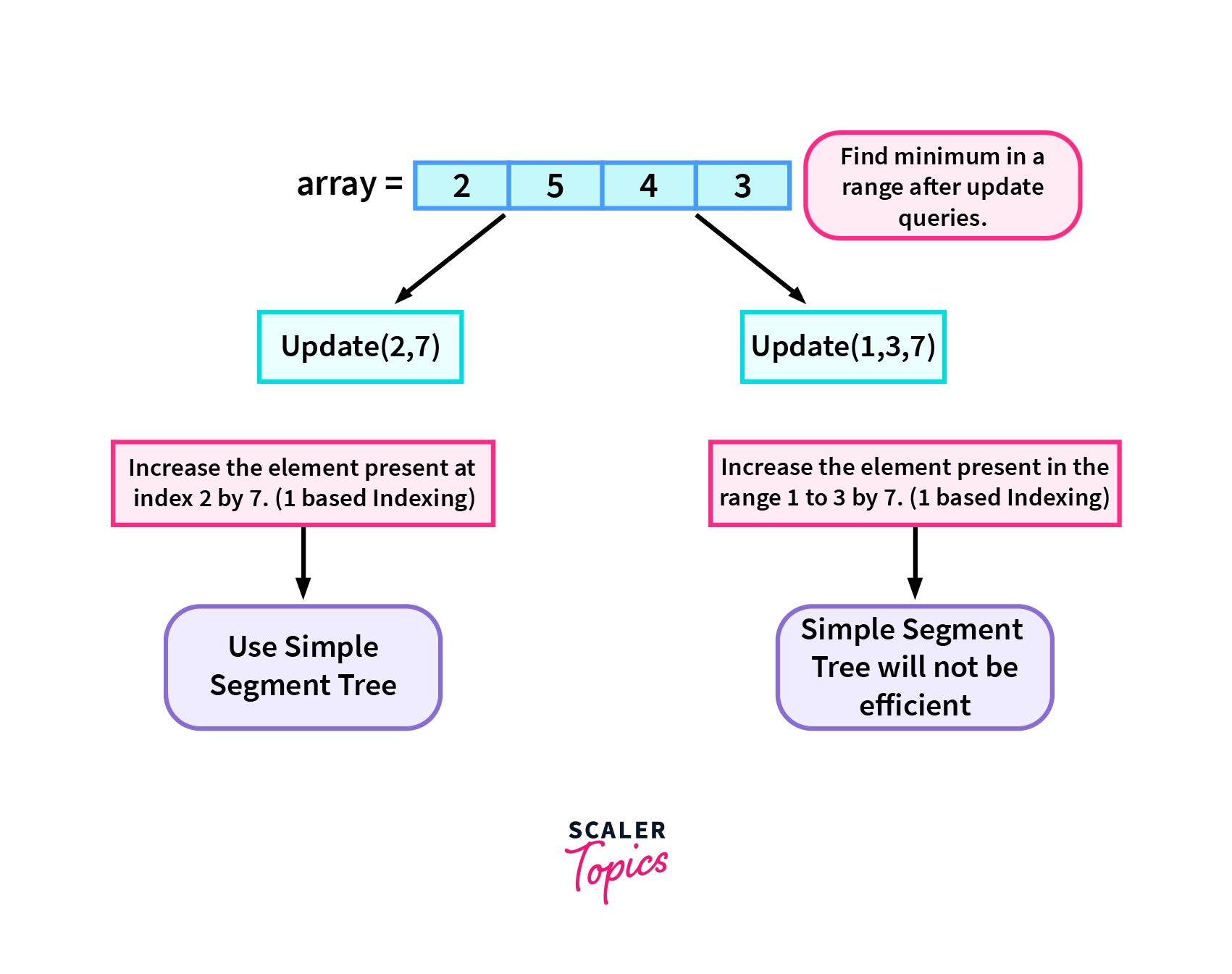
Another way to solve the above problem can be to traverse the given range in the array and update each element for every update query. Then find the minimum for the given range by again traversing the entire range in the array. This will take a time complexity of O(N) as we are traversing the array for each update query. However, if there are Q such queries the time-complexity will be O(Q*N).
Can we solve the above problem in a better complexity?
Yes, we can! We use the lazy propagation technique to solve the range update queries in O(log N) time complexity. Let us first discuss the structure of a segment tree and then understand the lazy propagation technique in a segment tree.
Structure of a Segment Tree.
A segment tree is a binary tree in which every node is associated with a certain range. The interval associated with the child nodes is approximately half the size of the interval associated with the parent node.
We can visualize the structure of the segment tree as follows-
- Every node is associated with some intervals of the parent array. Parent Array refers to the array from which the segment tree is built.
- The root of a segment tree represents the entire array. i.e [0,n-1] (0 based indexing).
- Every leaf node is associated with a single element which is an element of the array.
- The intervals associated with any two child nodes of a given node are disjoint.
- The union of two child intervals gives us the interval associated with the parent node.
- If we consider the root node to be indexed at 0. The left and right children of a node will be given by 2*parent_id+1 and 2*parent_id+2. We can also consider the root node to be indexed at 1. Then the index of the left and right children of a node will be 2*parent_id and 2*parent_id+1. Here parent_id is the index of the parent node.
Below is a visual representation of a segment tree used for minimum range queries.
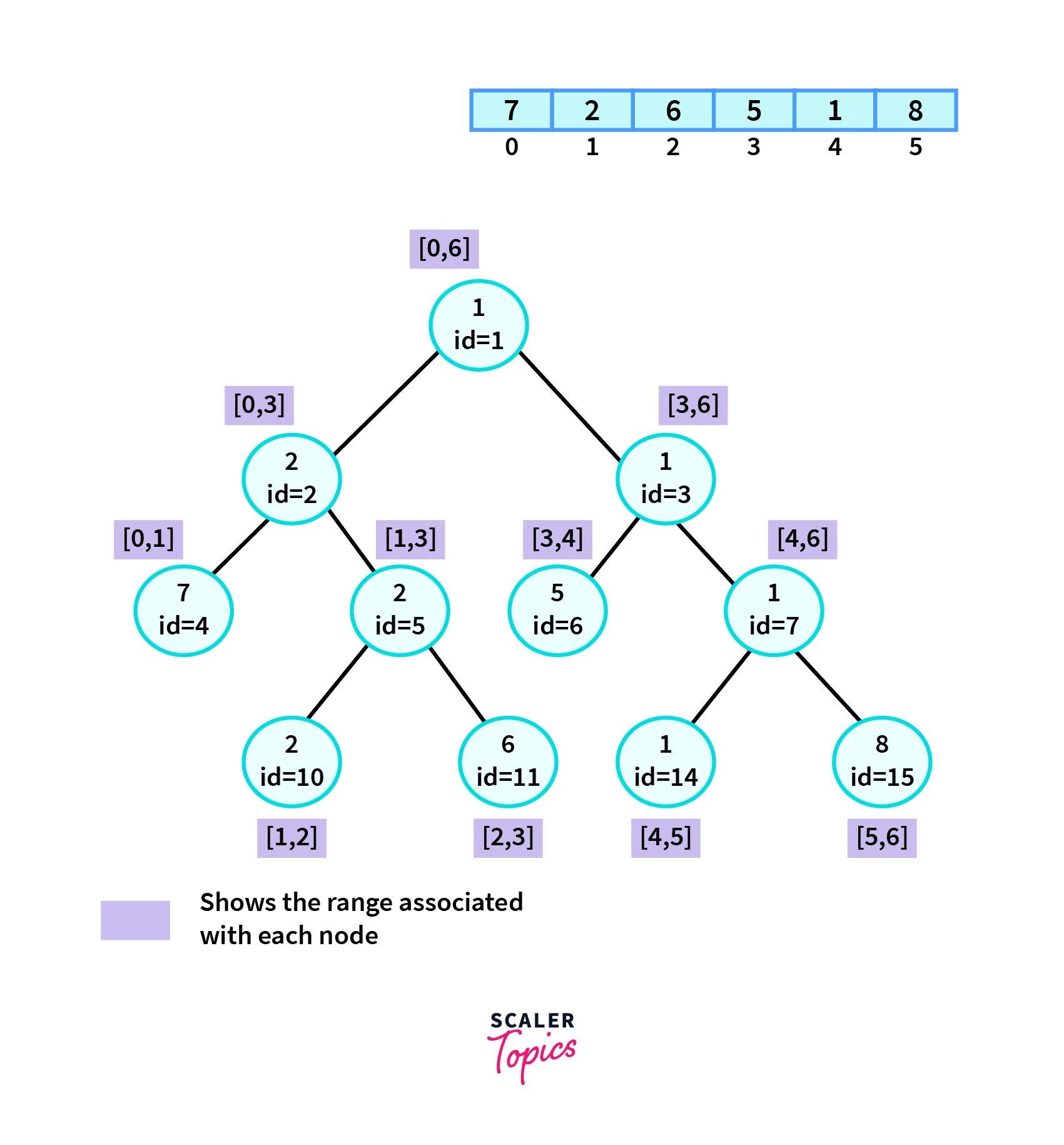
In the Segment Tree shown above, we should note that we have used 1 based indexing for the root node. Each node's associated range is taken as left range inclusive and right range exclusive. That is Range [Left_Range, Right_Range) means [Left_Range, Right_Range-1]. The leaf nodes of the tree represent the array element from which the tree is made. Whenever the number of elements in the array is not a power of 2 some underlying subintervals may not be completely filled.
Why a simple segment tree can't be used for handling Range Updates efficiently?
Let us recall how a segment tree for point update works!
- To update a single element in a segment tree we need to move to the leaf node corresponding to that element in the original array.
- After updating that particular element in the parent array and in the segment tree we backtrack.
- While backtracking we updated all the values associated with that node in the segment tree.
However, in range updates, we need to update multiple elements at a time. So this means that we need to move to the leaf node associated with each element to be updated in the range. Let's suppose that the range to be updated consists of all the elements present in the array. Thus updating all the elements one by one would take a time complexity of O(N * log N). This is because one updating query for a point update using the Segment Tree takes O(log N) time. Handling N such elements in a single query would make the time complexity O(N * log N ) for a range update. This time complexity is even less efficient than the brute force approach discussed above which takes O(N) time complexity for an updating query.
Thus simply using a segment tree will not help us to solve range updates efficiently. Let's see how can we handle range updates in a more efficient manner.
Solving Range Updates with Lazy Propagation Technique
The conditions of No Overlap, Partial Overlap and Complete Overlap will be the same as those discussed for a Simple Segment Tree.
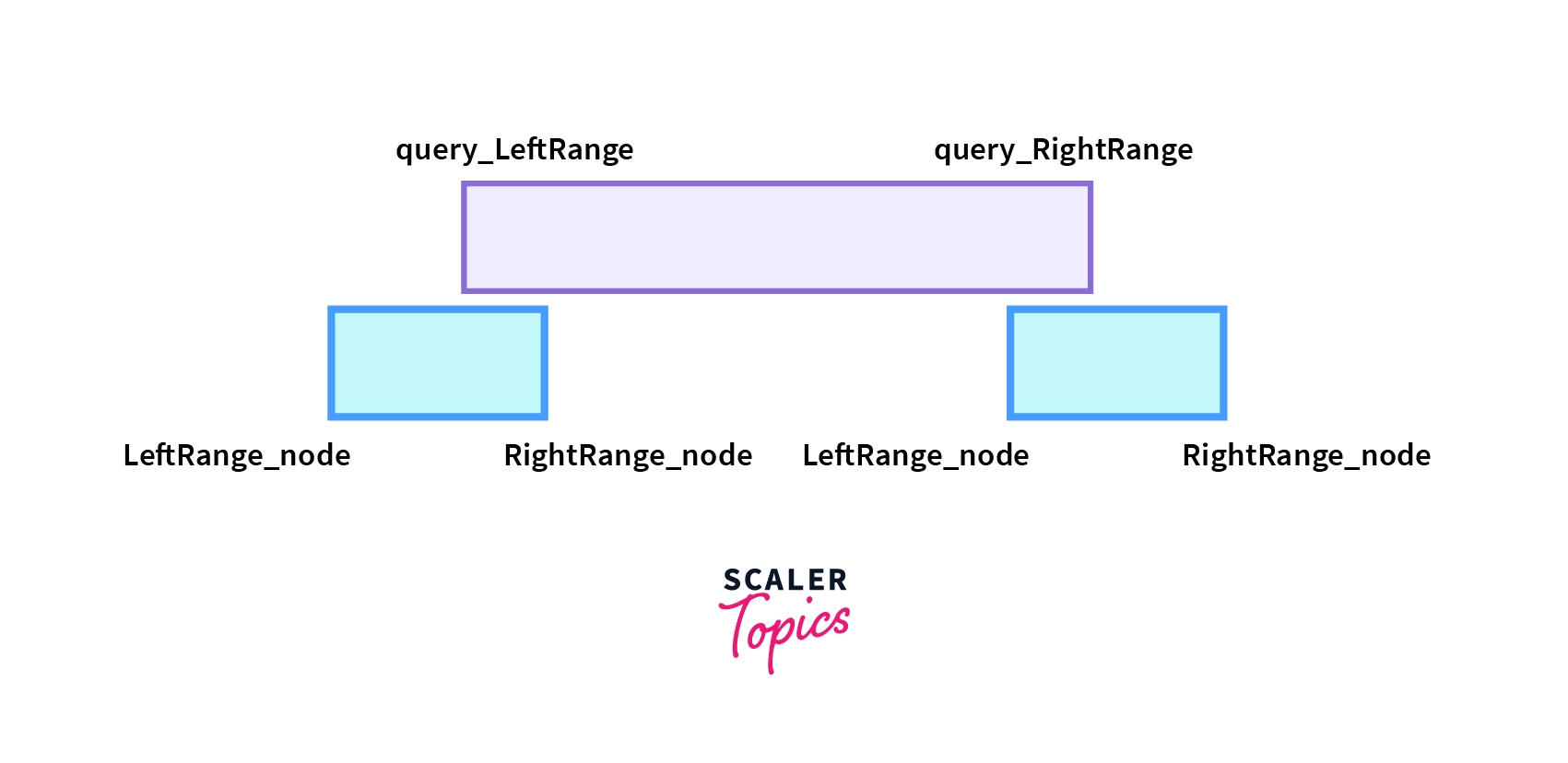
- No Overlap: The range associated with node falls completely outside the range asked in the query. i.e RightRange_node <= query_LeftRange or LeftRange_node >= query_RightRange.
Note that we are taking equal to as we are taking the ranges as right range exclusive and left range inclusive manner.
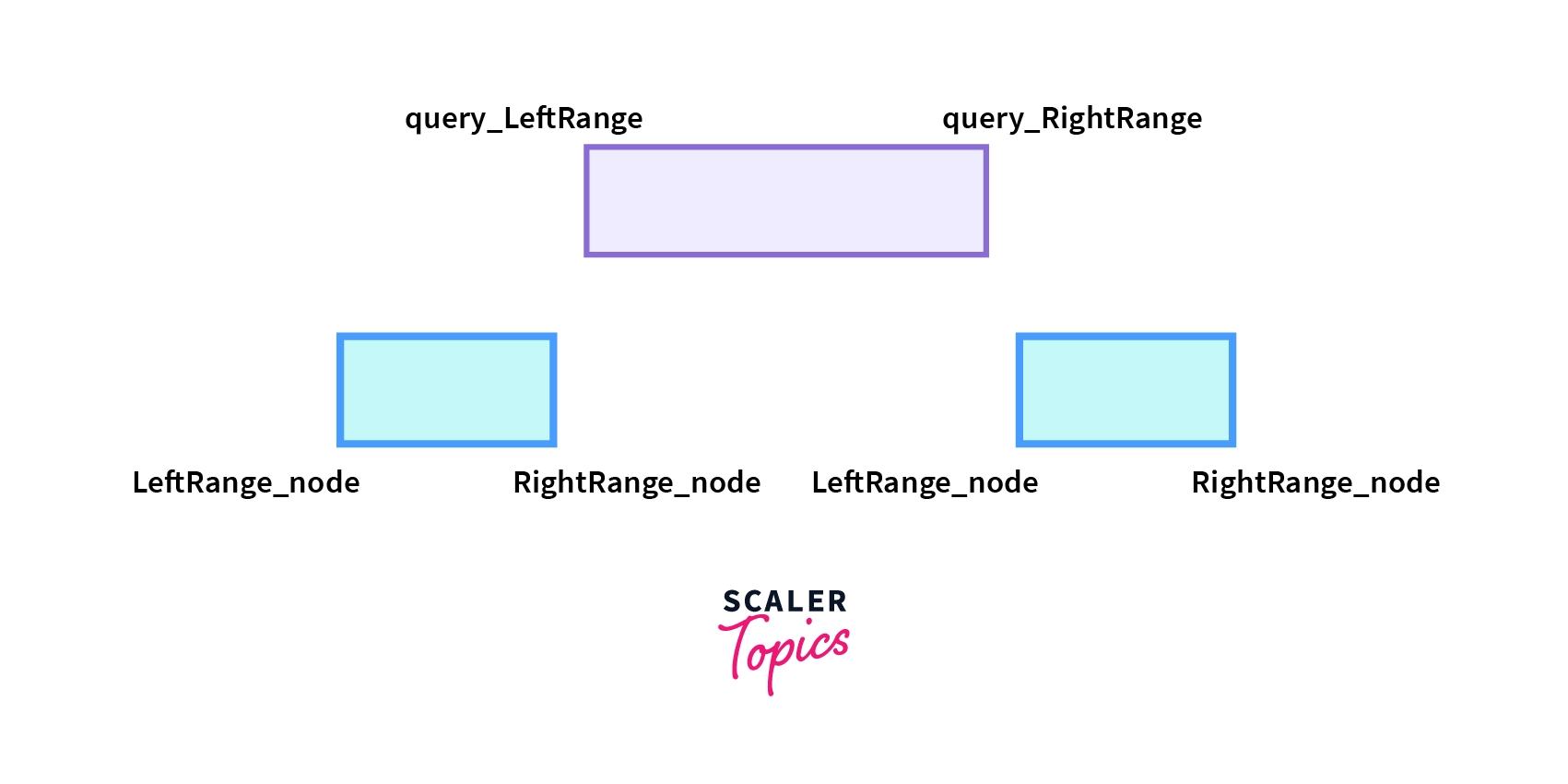
- Complete Overlap: - The range associated with node falls completely inside the range asked in the query. i.e LeftRange_node >= query_LeftRange and RightRange_node <= query_RightRange.
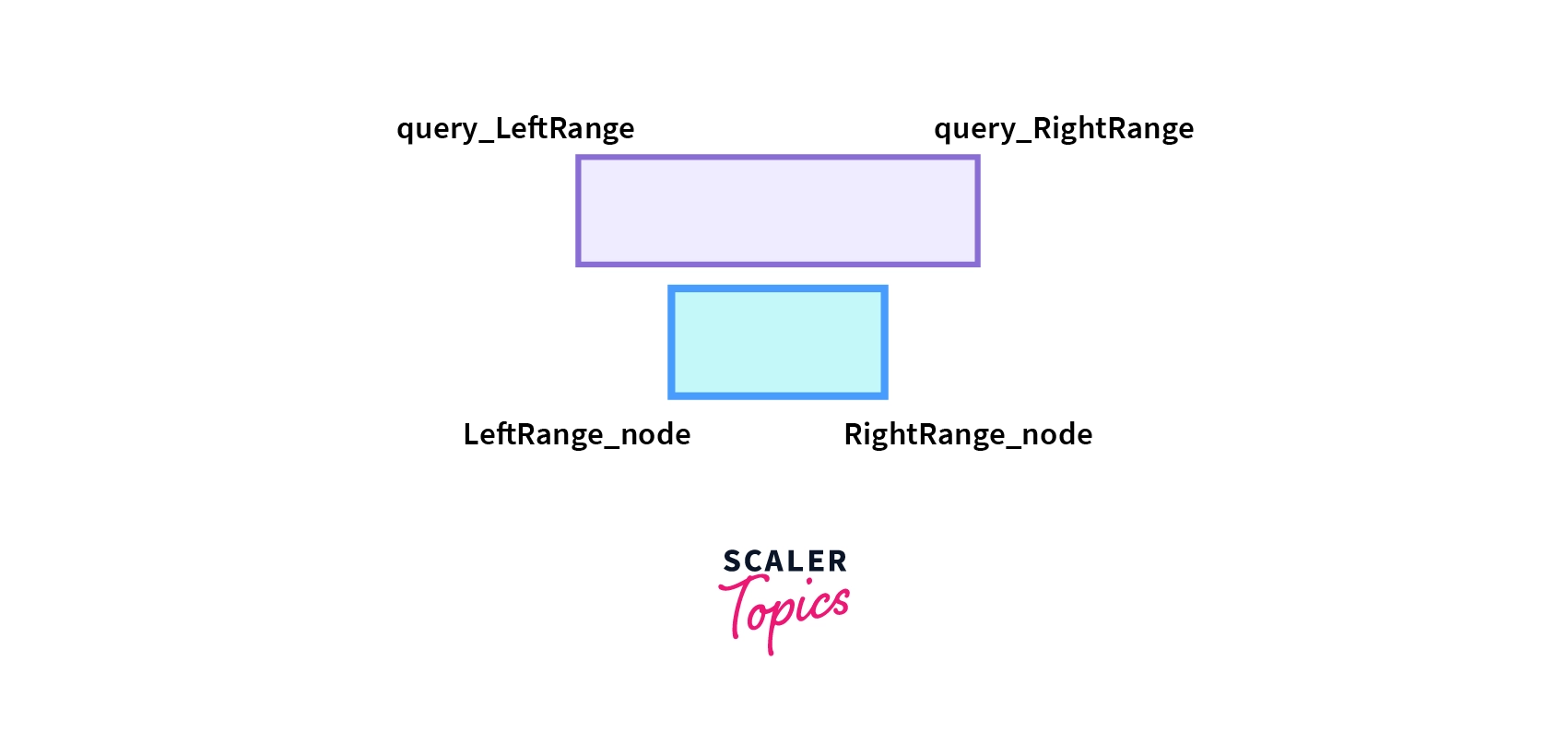
- Partial Overlap: - The range associated with the node falls partially inside and partially outside the range asked in the query. If both the above condition fails it will be a case of partial overlap.
Let us look at the approach used to solve Range Updates using Lazy Propagation. Consider the array as, array=[3,7,6,4]. Let us build a minimum segment tree for this array. Refer to the segment tree shown below.
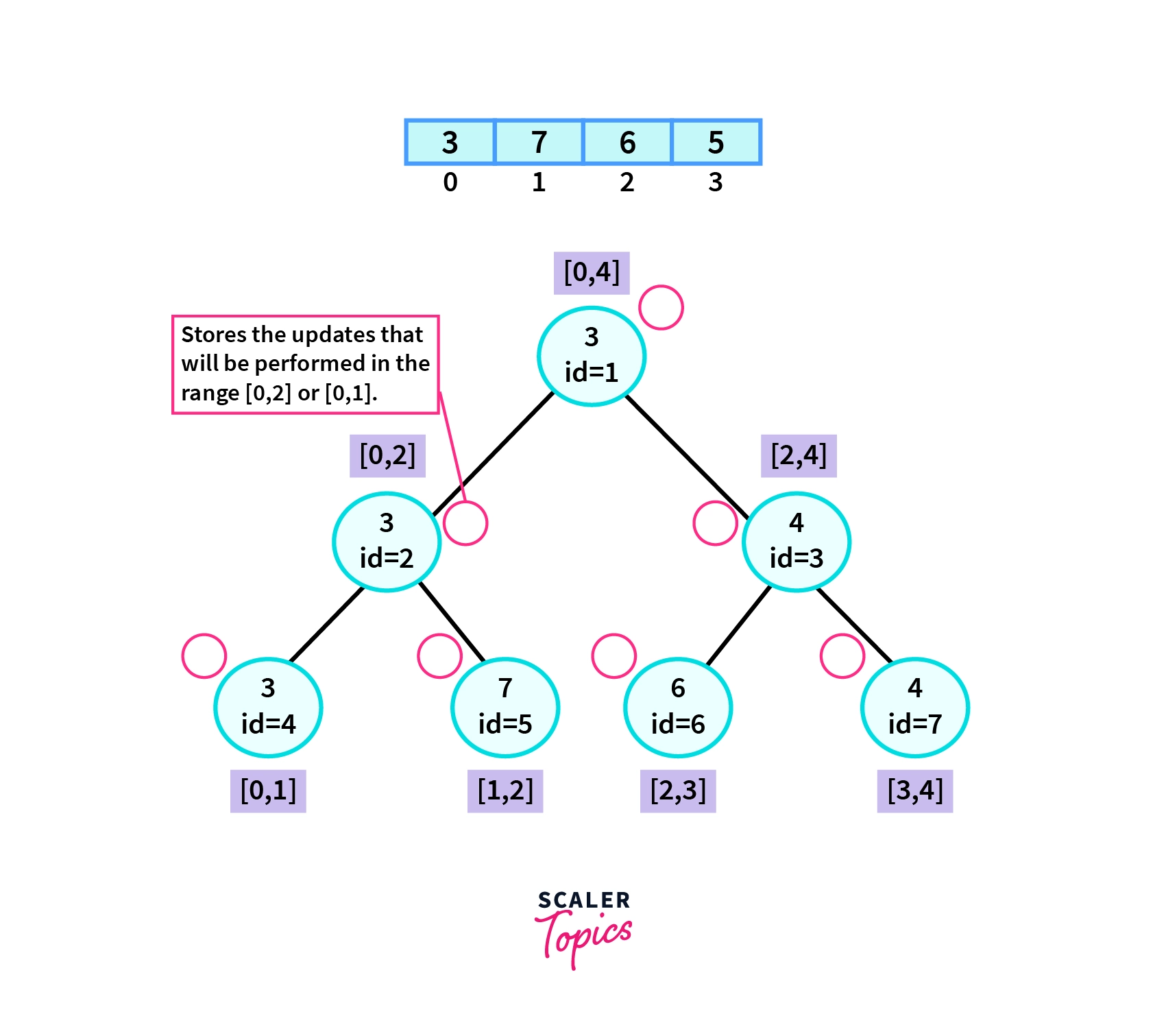
To use Lazy Propagation in a segment tree we make copies of each node. The copy nodes are represented by red circles beside every node in the segment tree. The range and the id associated with the copy nodes are the same as that of the nodes in the Segment Tree. These copy nodes will store the information about the updates that we need to perform in a given range. We will use these copy nodes to suspend the updates for the future and use them whenever they are required in the query. This is what lazy actually means. We suspend the updates for the future by being lazy at the present. We use an additional vector or an array to store the copy nodes. Let’s name this vector as LazyPropagationVector. Now let’s understand how we can apply Range Updates using Lazy Propagation.
Implementing Range Update function
Let's define a function LazySegmentTreeRangeUpdate(updateValue, LeftRange,RightRange), which means that we need to increase every element present in the range [LeftRange, RightRange-1] by updateValue. Note that in this function we are taking left range inclusive and right range exclusive.
Now let us implement the function LazySegmentTreeRangeUpdate(5, 0, 2). That is we need to increase every element present in the range 0 to 1 by value 5 (0 based indexing). Refer to the diagram shown below.
LazySegmentTreeRangeUpdate(5, 0, 2)
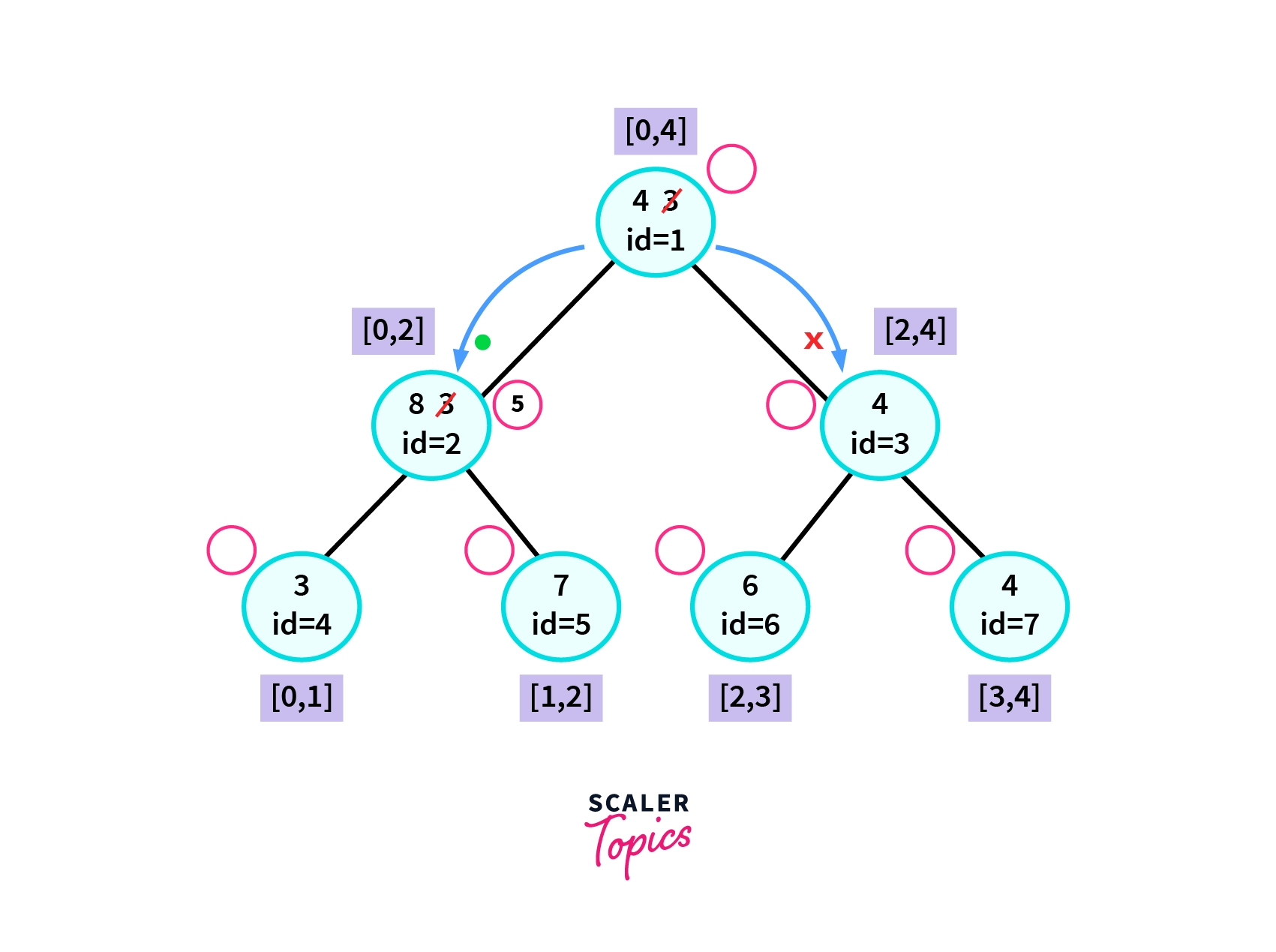
- The blue arrows show the direction of the dfs traversal.
- The cross represents the condition of no overlap from where we return in our dfs call.
- The green dot represents the condition of complete overlap.
We return from our dfs call in the case of complete overlap and no overlap of intervals.
- We start our dfs traversal from the root of the segment tree, i.e node with id equal to 1.
- From the root node, say we move to its left that is the node with id=2.
- Since we get a condition of total overlap we increase that node of the segment tree by 5.
- Here we use the distributive property of minimum function over addition. That is we can write minimum(3+5,7+5) as minimum(3,7)+5.
- We also update the copy node associated with that node of the segment tree. By doing this we are preventing the need of moving to every leaf node associated in the range to be updated. As storing 5 in the copy node associated with the node of id=2 will also mean that we need to add 5 in the range [0,1].
- While backtracking in our dfs call we update the non-leaf nodes with the minimum of both left and the right child to get the updated segment tree. We update the node with id=1 with the minimum of its left and right child.
- In the future, if we need the value of the node associated with the range [1,2), i.e element at index 1 of the parent array. We would first need to increase that value by 5 and then return the value.
LazySegmentTreeRangeUpdate(6, 0, 1)
Let's implement the function LazySegmentTreeRangeUpdate(6, 0, 1) in the segment tree obtained after the above operation. LazySegmentTreeRangeUpdate(6, 0, 1) means that we need to increase the element present in the range [0,0] or the element present at the 0th index of the array by 6 (0 based indexing). Refer to the diagram shown below.
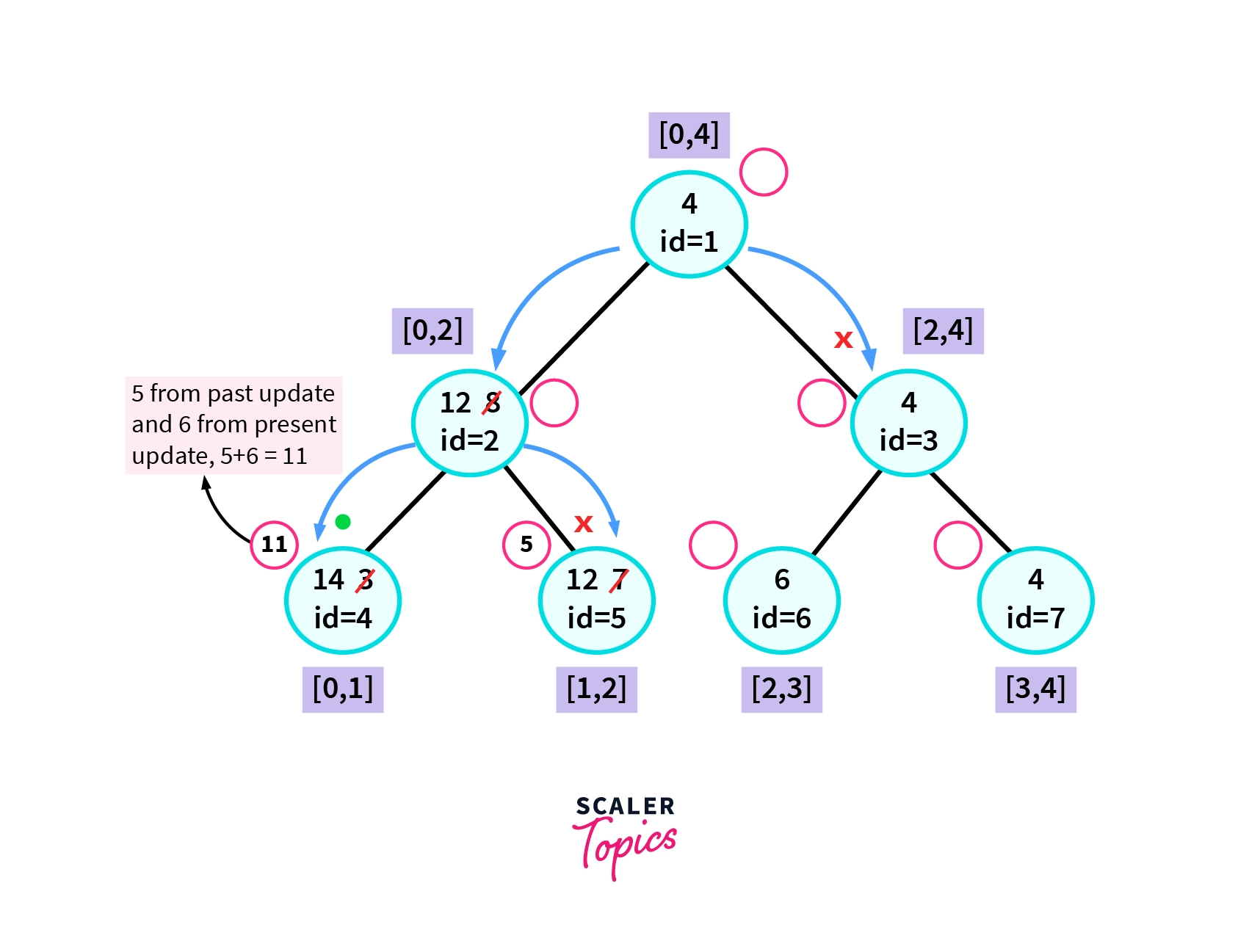
- We start the dfs call from the root of our segment tree. Say we move to its right, i.e node with id=3. We get a condition of no overlap. So we stop the dfs call and return.
- Then we move to its left child, i.e the node with id=2. Here we get a condition of partial overlap. Therefore we should move to its left and right child.
- However, before moving further in the dfs call we can see that an update is pending from the past. We can see this from the value present in the copy node associated with the node of id=2.
- Since the copy node is not empty we need to apply these updates to both the children nodes before moving any further in the dfs call. That is we need to increase the nodes with id=4 and id=5 by the value present in the copy node, i.e 5, and also update the copy nodes associated with them.
- After updating the nodes the value present at the node with id=4 becomes 3+5=8, and the value present in the node with id=5 becomes 7+5=12. Both the copy nodes associated with them will store the value 5.
- After updating the value of the nodes and the copy nodes we move to the left and right child of the node with id=2. When moving right we get a condition of no overlap in the node with id=4 shown by a cross in the diagram. So we return.
- Then we move to the left where we get a condition of total overlap. So we increase that node of the segment tree by 6 and also update the value of the copy node. That is the value present in the node with id=4 becomes (3+5)+6=14 and the value present in the copy node becomes 5+6=11.
- Note that the value present in the copy nodes of the leaf nodes will never be used. This is because we propagate the value present in the copy nodes only when we move to the child nodes. However, since leaf nodes don't contain child nodes its value will never be used.
Pseudocode for LazySegmentTreeRangeUpdate(updateValue,LeftRange,RightRange)
Let us understand the algorithm we will use to solve range updates with the help of its pseudocode. Note that entire implementation of the algorithm is discussed below in this article.
Solving Minimum Range Queries with Lazy Propagation
Solving range minimum queries for a segment tree with lazy propagation is the same as that of a simple segment tree. However, when moving to the child nodes of a particular node we need to make sure that past updates are not pending for the child nodes. We can do this by checking the value present in the copy nodes. If they are not empty we propagate its value to the child nodes and then solve the query. Let us look at an example for a better understanding.
Range Minimum Query using Segment Tree
Let's define a function LazySegmentTreeRangeMinimum(LeftRange,RightRange) as the minimum in the range from LeftRange to RightRange-1 ,i.e [LeftRange,RightRange-1] in the parent array (0 based indexing). Let's consider the segment tree shown below.
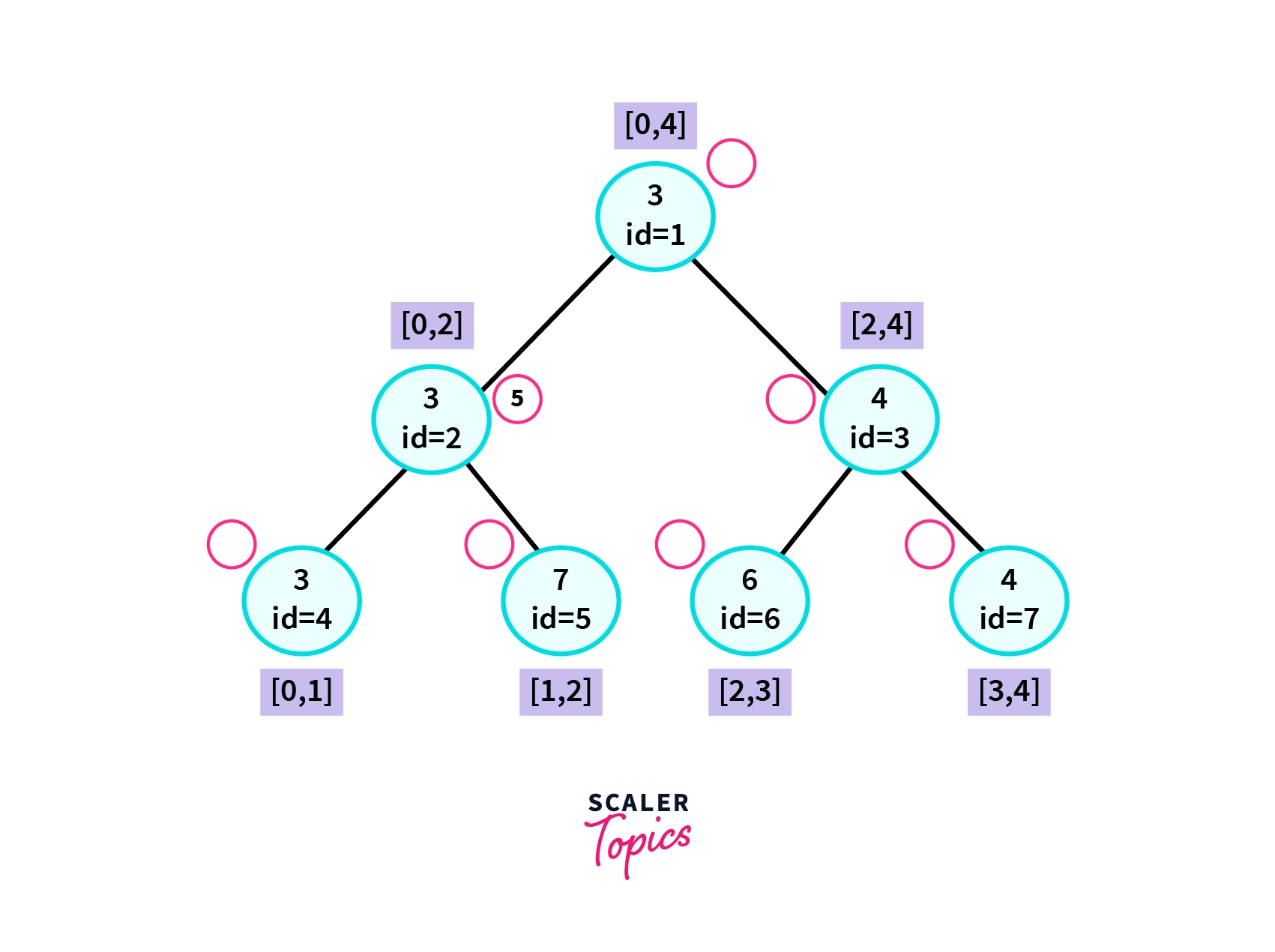
It is the same segment tree obtained after the operation LazySegmentTreeRangeUpdate(5, 0, 2) on the original segment tree. Now lets implement LazySegmentTreeRangeMinimum(0,2) on the given segment tree. That is finding the minimum in the range [0,2) after all the elements in the range [0,2) were increased by 5.
LazySegmentTreeRangeMinimum(0,2)
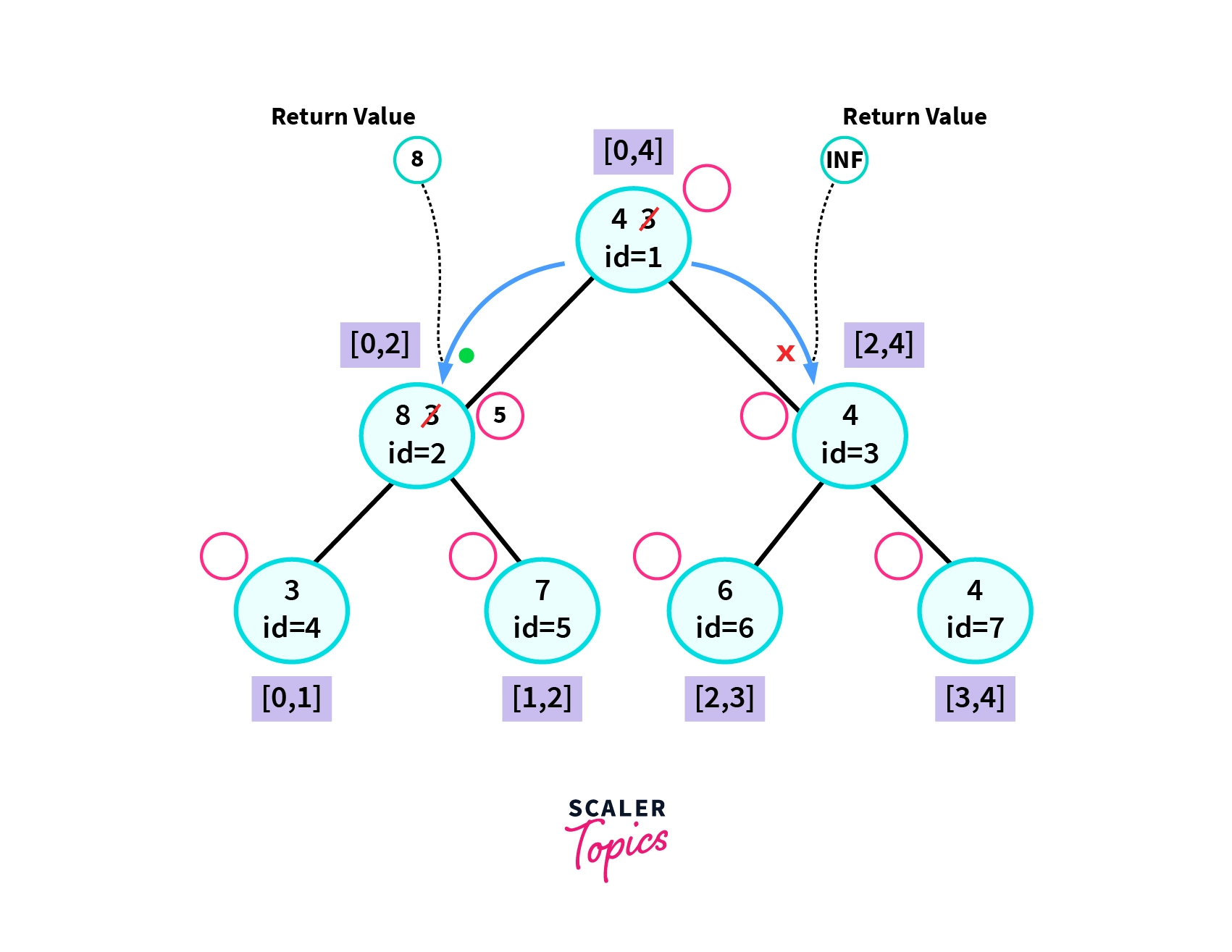
In the segment tree shown above, dotted lines represented the value returned from the dfs call. We will start our dfs call from the root node. Since the copy node associated with the root node is empty we can move towards its child nodes. Say we move towards the left child, that is the node with id=2. Here we get a condition of total overlap so we return the value present in the segment tree, i.e 8.
Next, we move towards the right child, that is the node with id=3. Here we get a condition of no overlap. So we return a value such that it will never affect our desired result. In the case of the minimum function, we return Infinty represented by INF in the diagram shown above.
Finally, we compute the minimum of 8 and INFINITY and return the result. That is minimum(8, INFINITY) = 8. So we return 8 as our answer which is the correct result.
We can see that the lazy propagation approach can be used to solve the minimum range queries in a much efficient way without affecting the correct result. It is efficient than the brute force approach as we are not updating every leaf node in the range update queries, but we are suspending the updates for the future by storing the updates in the copy nodes.
Pseudocode for LazySegmentTreeRangeMinimum(LeftRange,RightRange)
Below, we have shown the pseudocode for LazySegmentTreeRangeMinimum(LeftRange,RightRange) function. Note that we will discuss the entire implementation of the algorithm after this section.
Implementation of Range Minimum Query in Segment Tree using Lazy Propagation
Let us see how we can solve range minimum queries with range updates efficiently using lazy propagation.
- At first we build our minimum range segment tree. The build function is the same as that used for a simple segment tree with point updates. We will use buildSegmentTree function to build the minimum range segment tree. Whenever we get a node with RightRange-LeftRange=1 we get a leaf node. In such a case we update that node with its corresponding value in the parent array, i.e element indicated by LeftRange.
- Whenever the query string is RangeUpdate we will use the LazySegmentTreeRangeMinimum function to update the range query_LeftRange to query_RightRange-1 with updateValue.
- Whenever the query string is RangeMinimum we will use the LazySegmentTreeRangeMinimum function to return the minimum in the range of query_LeftRange to query_RightRange-1.
- Note that we will have to use long long data type for larger inputs and also update the value of infinity with a larger value.
C++ Implementation-
Complexity Analysis in a Segment Tree
Space Complexity
What is the maximum number of nodes that can be associated with a Segment Tree?
Let's think a maximum of how many nodes will be required in a Segment Tree. The root node will consist of two children nodes let’s name this as layer 1. The two nodes of layer 1 will again have their own children nodes. Thus total nodes in layer 2 will be 4 nodes. This will go on until we reach the leaf nodes which will represent the array elements. So in the worst case, the number of nodes in the segment tree can be represented as the sum of
So we have proven that the maximum number of nodes in a segment tree will never exceed 4*n. Where n is the number of elements of the parent array. Since we are using two vectors SegmentTree and LazyPropagation to store the nodes of the tree and the updates. Thus the Space complexity in the array representation of a Segment Tree is O(n).
Time Complexity
Build Query -
A Segment tree can contain a maximum of 4*n+1 nodes (1 based indexing). As we visit every node once while building the Segment Tree. Hence the time complexity of the build function is O(n).
Range Minimum Query -
The time complexity for a range minimum query is also the same as that in a simple segment tree. If propagating the past updates takes O(1) time-complexity, i.e addition in this case. A Range Minimum Query will take O(log n) time complexity.
Range Update Query -
We are not updating every leaf node present in the range query but updating only one node associated with the entire range. We can come across log n such nodes. And if the operation we are doing takes O(1) time, i.e addition in this case. A Range Update Query will take a O(log n) time complexity.
Conclusion
- Lazy Propagation Technique can be used to solve Range Update Queries in O(log n) time complexity.
- The same logic can be used for other associative and distributive functions as well.
- This includes addition over a range and finding minimum, range multiplication and sum of a range, range addition and sum of a range, range bitwise OR and bitwise AND of a range and many such queries.
- A segment tree is a very flexible data structure and allows different modifications and extensions to solve a variety of functions in an efficient way.
