Shortest Path in Directed Acyclic Graph

In graph theory, identifying the shortest path from a single vertex to all others is essential. The Bellman-Ford algorithm accomplishes this in O(V×E) time. However, for Directed Acyclic Graphs (DAGs), topological sorting offers a more efficient approach.

Before delving deeper, let's understand what a Directed Acyclic Graph (DAG) is. Essentially, it's a directed graph free of cycles, as illustrated in the upcoming image.

This article will delve into how to find the shortest paths in a weighted DAG. Understanding DAGs, which are directed graphs without cycles, is crucial for grasping complex network structures in computer science.

Intuition

For general weighted graphs, we can use the Bellman Ford algorithm to find single source shortest paths in $O(V\times E)$ time. But here we have been given a special property of the graph that it is a Directed Acyclic Graph so we will utilize this property to perform our task in an efficient way. The idea is to use Topological Sorting.

Once we have the topological order of the given DAG, we will process the vertices in the same order. Here, processing a vertex means, updating distances of its adjacent vertices using the distance of the current vertex from start.

Algorithm

Topological Sort

1. Create a Stack (say st) which will be used to store the topological ordering.
2. Create a boolean array (say visited), it will be used to mark the vertices which have been visited.
3. For each unvisited vertex (say node) from 0 to V-1 call a recursive helper function which will do the following:
   • Mark node as visited.
   • For each adjacent vertex of node call the recursive function.
   • Push node in st.

Shortest Path

1. Find topological ordering of the given graph
2. Create an array (say dist) of size V, and initialize all its entries with a very large number (say INF).
3. Traverse over all the vertices in topological order and for each vertex u, check the following conditon for all the adjancent vetex v of u If ( dist[v] > dist[u] + weightOfEdge(u$\rightarrow$v)) then dist[v] =dist[u] + weightOfEdge(u$\rightarrow$v)

Example

Consider the below given Directed acyclic graph and let's say we need to find the shortest distance of all vertices from vertex 0.

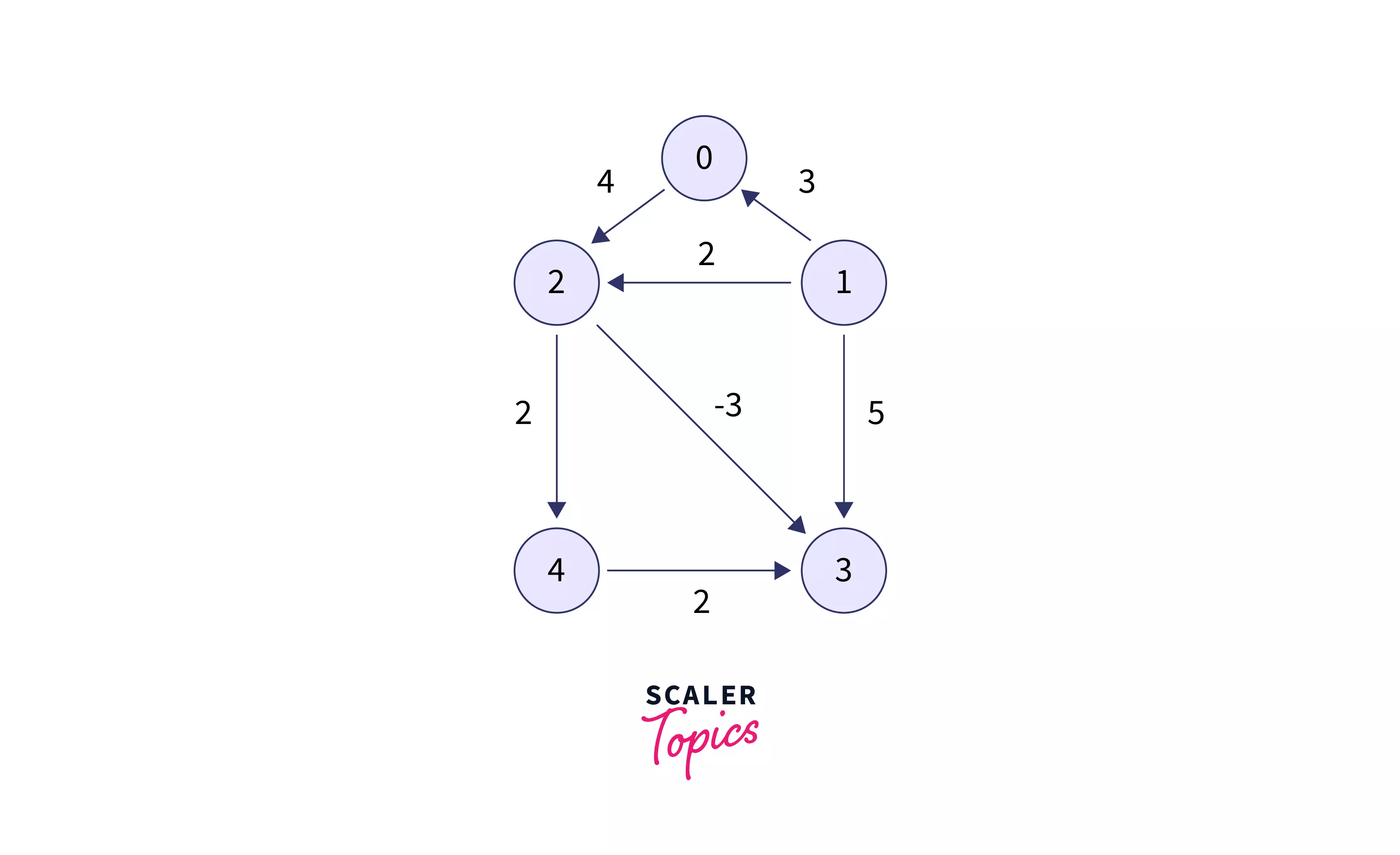
As per the algorithm discussed in the previous section, we will first find the topological sorting of this graph. topo = [1, 0, 2, 4, 3]

If you are finding any difficulty in finding the topological order please have a look at Topological Sort.

Now we will create an array dist of size V (here V=5) all entries of which will be initialized with INF. Then assign dist[start]=0. dist = [0, INF, INF, INF, INF]

The next step is to traverse vertices in topological order.

1. topo[0]=1 The adjacent vertices of 1 are 0, 2, and 3. So we will check the following:
   • If dist[0] > dist[1] + weightOfEdge(1 $\rightarrow$ 0), putting their values will give 0 > INF + 3, which evaluates to false.
   • If dist[2] > dist[1] + wightOfEdge(1 $\rightarrow$ 2), putting their values will give INF > INF + 2, which evaluates to false.
   • If dist[3] > dist[1] + wightOfEdge(1$\rightarrow$ 3), putting ther values will give INF > INF + 5, which evaluates to false. After these steps dist array will look like dist = [0, INF, INF, INF, INF]
2. topo[1]=0 The adjacent vertex of 0 is 2. So we will check the following:
   • If dist[2] > dist[0] + weightOfEdge(0 $\rightarrow$ 2) putting their values will give INF > 0 + 4, which evaluates to true hence we will assign 4 to dist[2]. After this step dist array will look like dist = [0, INF, 4, INF, INF]
3. topo[2]=2 The adjacent vertices of 2 are 3 and 4. So we will check the following:
   • If dist[3] > dist[2] + weightOfEdge(2 $\rightarrow$ 3), putting their values will give INF > 4 + (-3), which evaluates to true hence we will assign 1 to dist[3].
   • If dist[4] > dist[2] + weightOfEdge(2 $\rightarrow$ 4), putting their values will give INF > 4 + 2, which evaluates to true hence we will assign 6 to dist[4]. After these steps dist array will look like dist = [0, INF, 4, 1, 6]
4. topo[3]=4 The adjacent vertex of 4 is 3. So we will check the following:
   • If dist[3] > dist[4] + weightOfEdge(4 $\rightarrow$ 3) putting their values will give 1 > 6 + 2, which evaluates to false.
5. topo[4]=3 There are no adjancet vertices to 3 hence we will not do anything.

Finally the dist array will be dist=[0, INF, 4, 1 ,6].

Implementation

As discussed in the algorithm section we will be having two functions i.e. ShortestPath and TopologicalSort.

• ShortestPath -

It will take src as an argument that represents the start/source vertex. We will declare an integer array dist of size V all of its entries will be initialized with a very large number and dist[src] will be 0.

Then we will iterate over all vertices to find the topological ordering by calling the TopologicalSort function, which will store the order in a stack (say st).

Now we will iterate while st is not empty and each time we will pop an element from st (say u), then we will check if dist[u]!=INF which means if u is reachable from src. If the conditio is found true then we iterate for all adjacent vertices of u and check -

$\text{dist[u's Adjacent]}>(\text{dist[u]}+\text{Weight of Edge }(\text{u}\rightarrow\text{u's Adjacent}))$

If the condition is found true, then we will assign RHS to LHS.

At last, we will print the dist array, where dist[i] denotes the shortest distance of i from src.

• TopologicalSort - It is just like standard implementation of topological sorting, which takes three arguments Viz. v, visited array and Stack st.

Firstly we mark v as visited, then we will traverse all adjacent nodes of v, call the same TopologicalSort recursively if an adjacent node is not visited. At last, we will push v into Stack st.

Pseudocode

C/C++ Implementation

Java Implementation

Python Implementation

Complexity Analysis

• Time Complexity - For a graph $G=(V,E)$ time taken to find the topological ordering is $O(V+E)$. After that, for every vertex $V_i$ we run a loop to its adjacent vertices. So time taken in this step is also $O(V + E)$. Hence the overall time complexity is $O(V+E)$.

• Space Complexity - We are using a visited array of size $V$ and Stack which will be of size $V$, so the overall space complexity is $O(V)$.