Sparse Matrix

Overview
Sparse matrices are very useful entities in computer science, they appear in the fields of computer graphics, recommender systems, machine learning, information retrieval, maps and graph-based applications, social networks to count a few.
So sparse matrices are very useful in computer science as they appear so frequently, Hence, we will be addressing questions like what are sparse matrices, how they can be represented in various forms along with their implementations, and some other use cases.
Takeaways
Sparse matrices can be useful for computing large-scale applications that dense matrices cannot handle.
Definition
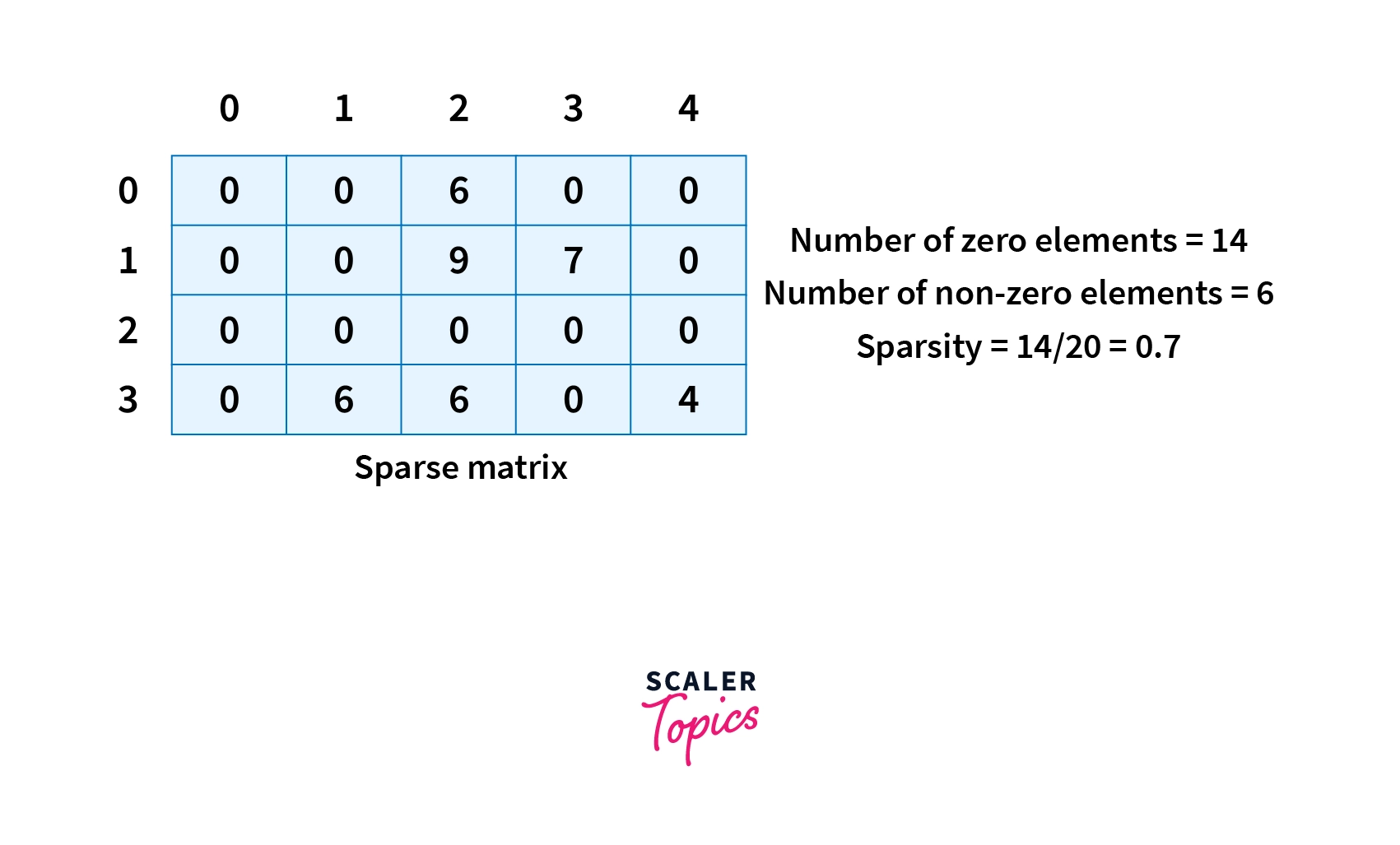
A matrix is defined as a 2-dimensional array having N rows and M columns where the order of this matrix is MxN (number of rows x number of columns).
A sparse matrix is defined as the matrix of order MxN which has the number of zero values strictly greater than the number of non-zero values, distinct from those matrices which contain more non-zero values than zero values, they are called dense matrices.
Sparsity:
The sparsity of a matrix is similar to the density of zero elements in the sparse matrix and is defined as the number of zero elements divided by the total elements of the matrix, calculated as:
sparsity = number of zero elements / number of total elements
The sparsity of a sparse matrix is always greater than 0.5.
The various domains of sparse matrices are, data preparation techniques like One-hot encoding , CountVectorizing, TfidfVectorizing ,sub-fields of machine learning like natural language processing and also for the optimized computation of lowest common ancestor problem in graphs.
Why do we need to use Sparse Matrix?
Highlights:
- 2-d Matrix representation uses excessive storage.
- As a consequence of excessive elements, it also takes excessive traversal time.
Storage:
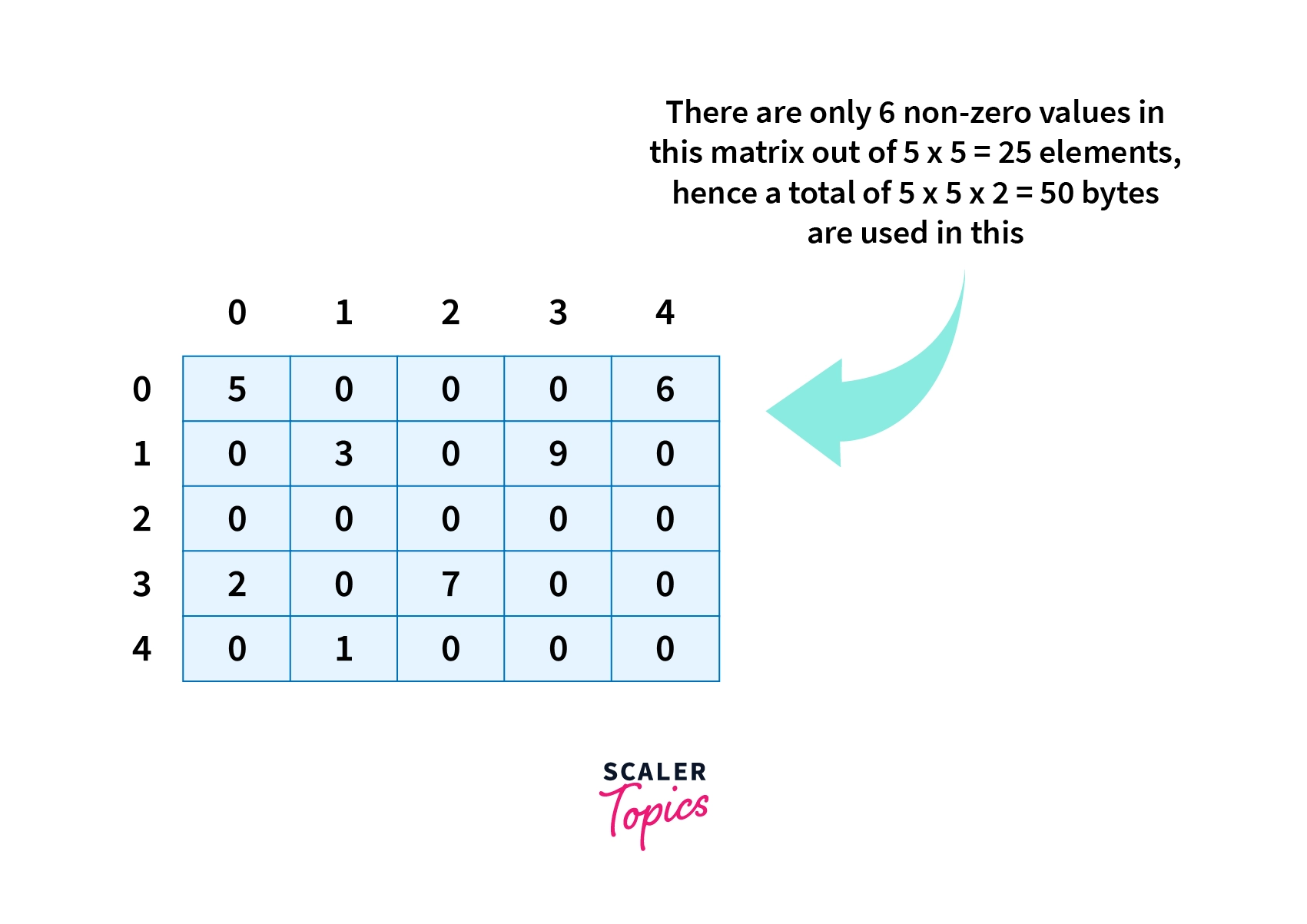
Since the sparse matrices are frequently occurring entities in many fields of computer science, they must be stored in some data structure, they are typically and most naively stored in the 2-dimensional array where each entry is represented by a[i][j], i represents the row number (numbered from top to bottom) and j represents the column number (numbered from left to right). But for an MxN matrix, the amount of memory it requires is proportional to MxN.
Assume a matrix of dimensions 100 x 100 containing integer values only and it has 10 non-zero values rest are all zeroes, then it will take 100 x 100 x 2 = 20000 bytes of memory to store these values.
Also, Zeros inside the matrices are of no use in the matrices, so a huge memory and processing are wasted on the zero values.
Processing time:
In the 2-d array representation of sparse matrix, In order to access the non-zero values, one needs to scan through all MxN values, hence it results in irrelevant scanning of zero elements because the positions of the non-zero elements are not specified.
Assuming the same matrix as in the previous example, traversing all 100 x 100 = 10000 elements requires scanning all of the 10000 elements making it to O(MxN) complexity.
In order to avoid the above problems and unnecessary computation, one needs to avoid the unnecessary scanning of the zero elements which appear in the 2-d array representation.
Therefore, one needs to design those type of data structures that only allows the storage of non-zero values.
Sparse Matrix Representations
Highlights:
- Triplet representation requires only "useful" elements.
- Similar idea is used for implementing linked list representation i.e. "useful" elements.
- Understanding the meaning of compressed forms of sparse matrices.
- Implementing two of those forms in the C++ programming language.
Keeping in mind the problems that appear in the 2-d array representation of the sparse matrix, the next obvious thought arrives is to simply avoid the storage of zero elements and store the non-zero elements.
Now, the follow-up question is "what information do we need to identify (access in O(1)) a non-zero element in a matrix?", and the answer is the row number i , the column number j.
Now, this derives the thinking to build a data structure that just stores this information about the non-zero values as follows:
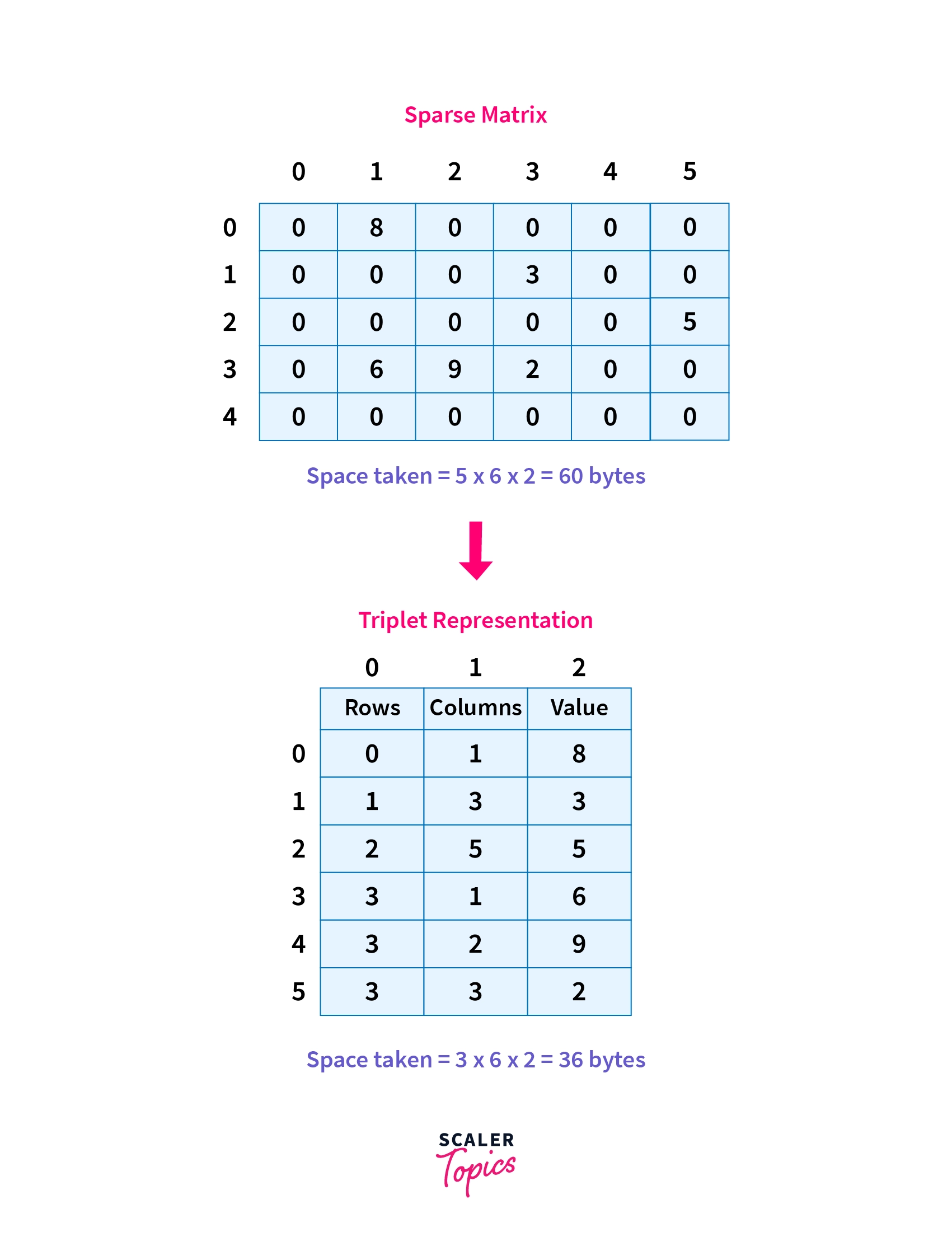
a)Triplet Representation(Array Representation)
Imagine a data structure that can store all information about non-zero elements namely row number i, column number j, and the value itself.
The most naive thought is a 2-d matrix having rows equal to the number of non-zero elements and three columns for storing the element and its position coordinates as shown below.
b)Linked List Representation
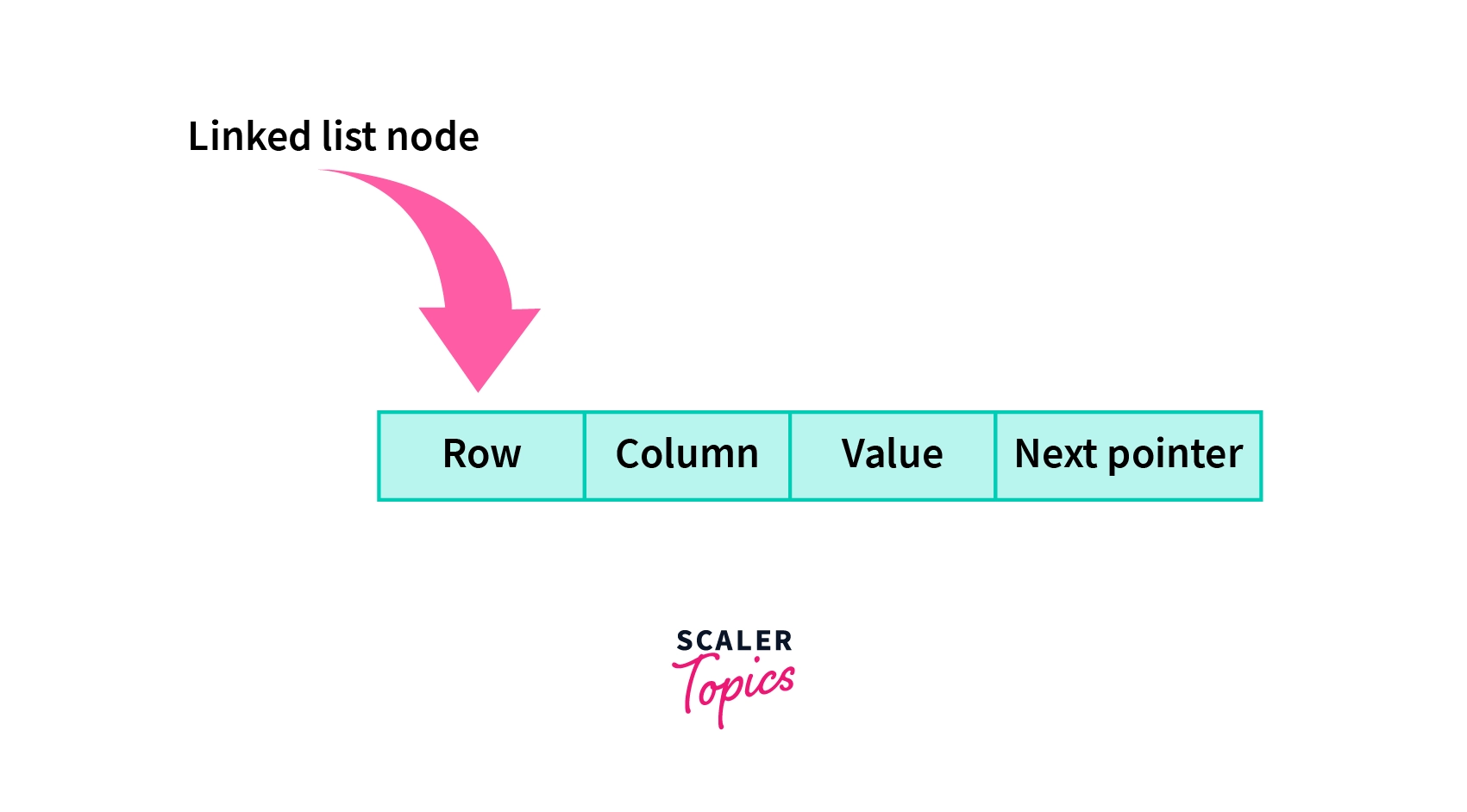
Imagine a linear data structure that can store all information about all non-zero elements namely row number i, column number j, and the value itself.
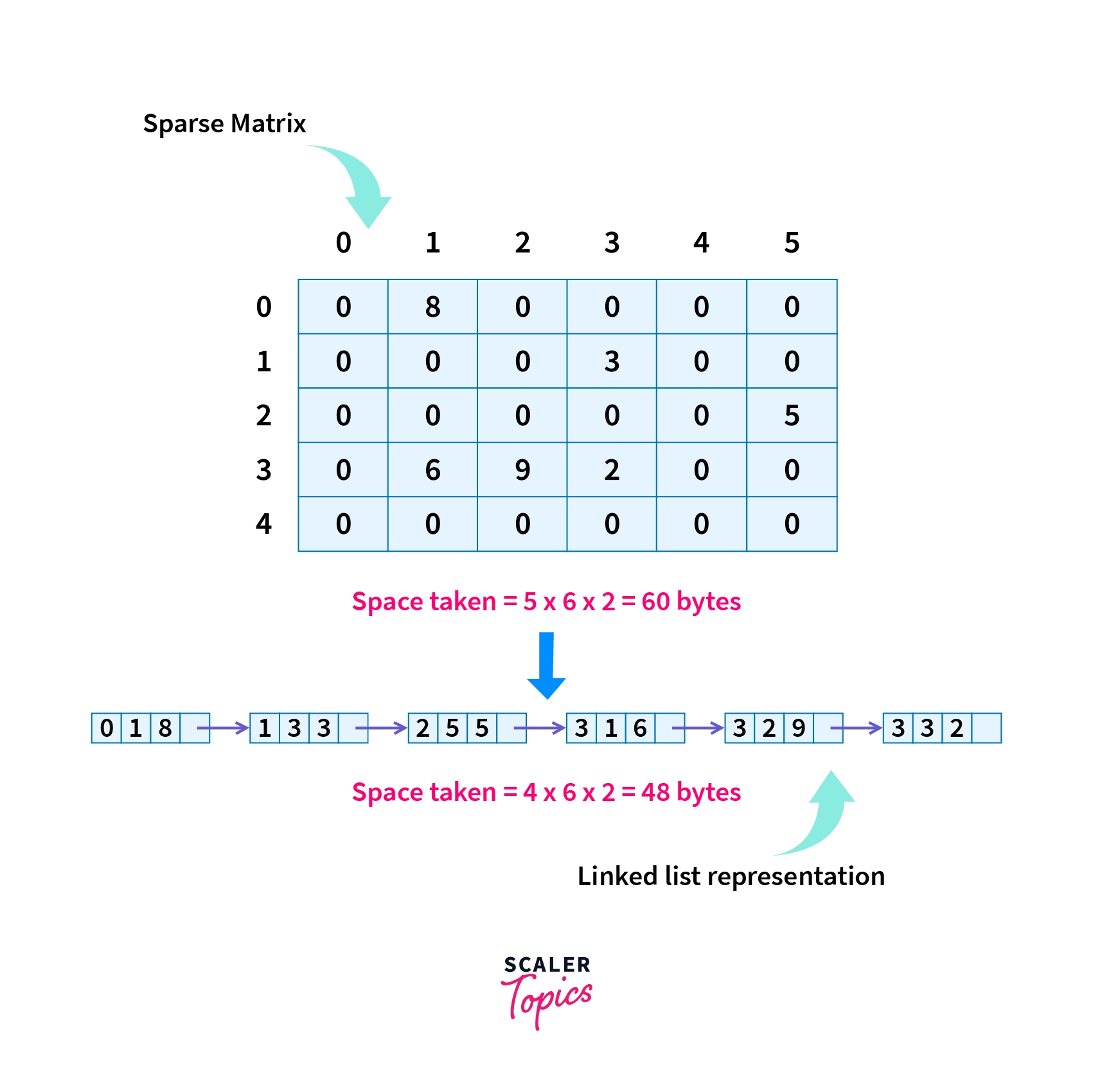
Besides array, a linked list can also be a good choice for storing the sparse matrix in a compressed form where each node of the linked list has exactly four entries containing row number, column number, the value of the non-zero element along with the pointer of the next node i.e. (i, j, value, next-pointer) as shown below.
The corresponding transformation from 2-d matrix to linked list representation is as follows:
Note:
Although there are many other representations of the Sparse matrix-like Dictionary of keys (DOK), List of lists (LOL), etc. we will be looking at the two of them only.
Array Representation (Triplet Representation) of Sparse Matrix
Highlights:
- Triplet definition in detail.
- Transformation from 2-d matrix representation to Triplet(Array) representation.
- Implementation of Triplet(Array) represntation in C++ programming language.
As we have seen the array representation or triplet representation is just another 2-d matrix similar to the original sparse matrix but with the number of columns limited to three each representing row, column and value of the element and number of rows equal to the number of elements, Hence, we have a N x 3 matrix where N represents the number of non-zero elements in the sparse matrix. As given in the last example we transformed a 5 x 6 matrix into a 6 x 3 matrix.
We can think of each non-zero element as a triplet i.e. an integer array of size 3 where the first element is the row number of the non-zero element, the second element is the column number and the third element is the value, and all non-zero elements can be represented as a stack of such triplets over each other hence making a N x 3 elements where N represents the number of non-zero elements.
Let's define the terminologies for each triplet:
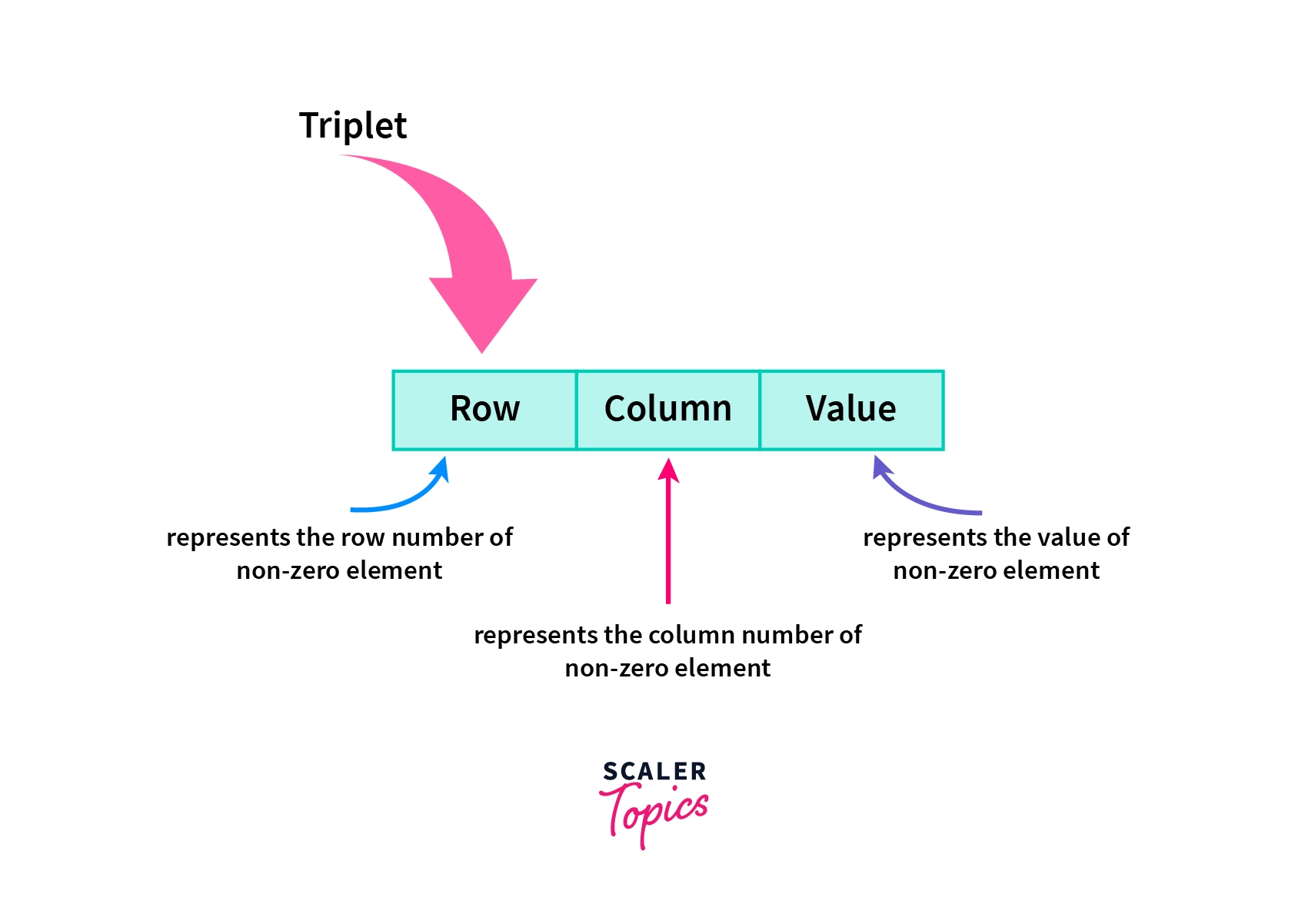
a) Row:
It is defined as the row number of the non-zero element counted from top to bottom when it is present in the 2-d array representation.
b) Column:
It is defined as the column number of the element counted from left to right when it is present in the 2-d array representation.
c) Value:
It is defined as the value of the non-zero element present at the (row, column) cell of the 2-d array representation.
Transformation of Sparse Matrix to Triplet Representation
Triplet(Array) implementation of sparse matrix
Triplet implementation is similar to the original sparse matrix i.e. it is also a matrix but of order 3xP where P represents the number of non-zero elements in the original matrix and 3 columns where the first column represents the row number, the second column represents the column number corresponding to the original sparse matrix which is of the order say M x N.
-
The number of non-zero elements i.e. P in the sparse matrix is calculated by traversing the original matrix in O(MxN).
-
Thus, the idea is to declare a 3 x P matrix, let's call it tripletMatrix[3][P], then traverse the original sparse matrix and for some ith non-zero element of the sparse matrix, tripletMatrix[0][i] is its row number , tripletMatrix[1][i] is its column number ,tripletMatrix[2][i] is its value considering 0-based indexing.
Let's see the C++ implementation of the tripletMatrix.
-
We are filling the tripletMatrix while traversing the original sparse matrix in O(MxN).
-
Initialize a variable k to zero which keeps track of the non-zero element count hence 0 <= k < P and while traversing the original matrix whenever a non-zero element is encountered then asssign it to the tripleMatrix as (tripletMatrix[0][k] = row number, tripletMatrix[1][k] = column number, tripletMatrix[2][k] = value) represents the kth non-zero element in the sparse matrix and increment k by 1.
-
Finally, display the tripletMatrix.
Linked list Representation of the Sparse Matrix
Highlights:
- Linked list node for each non-zero element.
- Transformation from 2-d matrix representation to Linked list representation.
- Implementation of linked list representation in C++ programming language.
This representation is another linear representation of the sparse matrix besides triplet representation in which each non-zero element of the sparse matrix is represented by a linked list node where the information about the non-zero element of sparse matrix namely row number i counted from left to right in the sparse matrix, column number j counted from top to down in the sparse matrix, the value of the element and the pointer to the next non-zero element i.e. next node of linked list is stored in the linked list node.
Thus, the sparse matrix is transformed into a linked list where each node contains a non-zero element.
Let's define the terminologies for the linked list node:
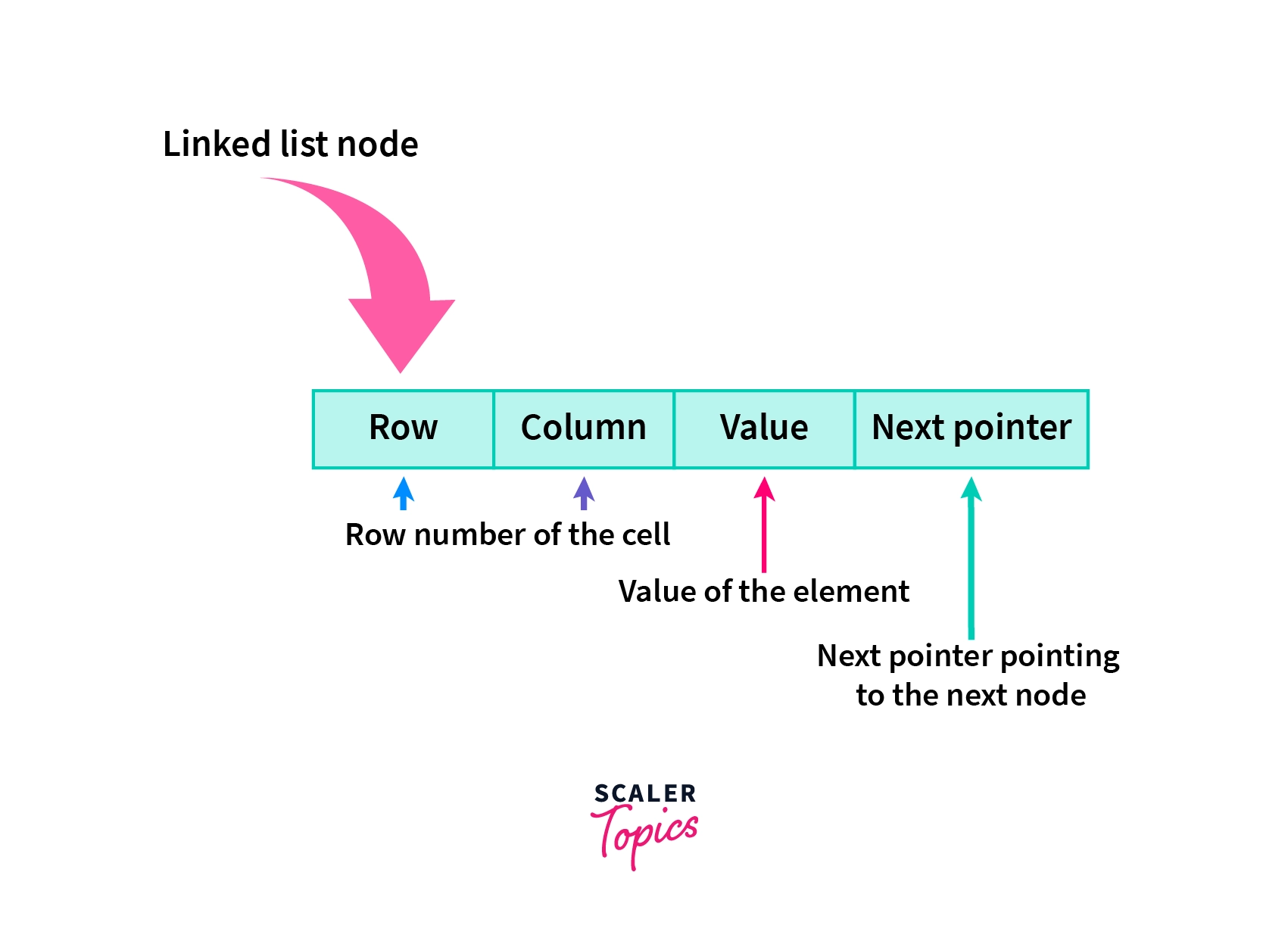
a) Row:
It is defined as the row number of the non-zero element counted from top to bottom when it is present in the 2-d array representation.
b) Column:
It is defined as the column number of the element counted from left to right when it is present in the 2-d array representation.
c) Value:
It is defined as the value of the non-zero element present at the (row, column) cell of the 2-d array representation.
d) Next pointer:
It is defined as the address of the next node in the linked list storing the next non-zero value.
Transformation of Sparse Matrix to Linked List Representation
Linked list Implementation of Sparse Matrix
Linked list implementation is also another compressed representation of the sparse matrix where each non-zero element is represented by each node of the linked list containing row number, column number, the value of the element, next pointer.
-
The number of non-zero elements i.e. P in the sparse matrix is calculated by traversing the original matrix in O(MxN).
-
Thus, the idea is to create a class of Node that stores the row, column, value, and a pointer of type Node which points to the next node.
-
Thus, using this class objects i.e. nodes of the linked list are created and each node is filled with the non-zero element of sparse matrix, and nodes are linked by the next pointer.
Let's see the C++ implementation of the Linked List implementation of Sparse Matrix.
- We are generating the linked list while traversing the original sparse matrix in O(MxN).
- While traversing, when a non-zero element is encountered then, a new node object is created using the Node class and the row number, column number, value of element are assigned to it then already created linked list is traversed up to the last node and this node is attached at the end, hence, this node is the new last node of the linked list which points to none.
Lowest Common Ancestor using Sparse Matrix and Dynamic Programming
Highlights:
- Sparse matrix is also called a sparse table.
- It is used to calculate the lowest common ancestor of two nodes a and b of an n-ary tree i.e. LCA(a,b) in time complexity.
- This technique is quite useful in programming contests, also called binary lifting/jumping.
The Lowest Common Ancestor (LCA) problem is a classical problem of finding the lowest common ancestor node in a general n-ary tree where LCA of two nodes say a and b is the lowest parent which is common to both nodes as shown in the figure below:
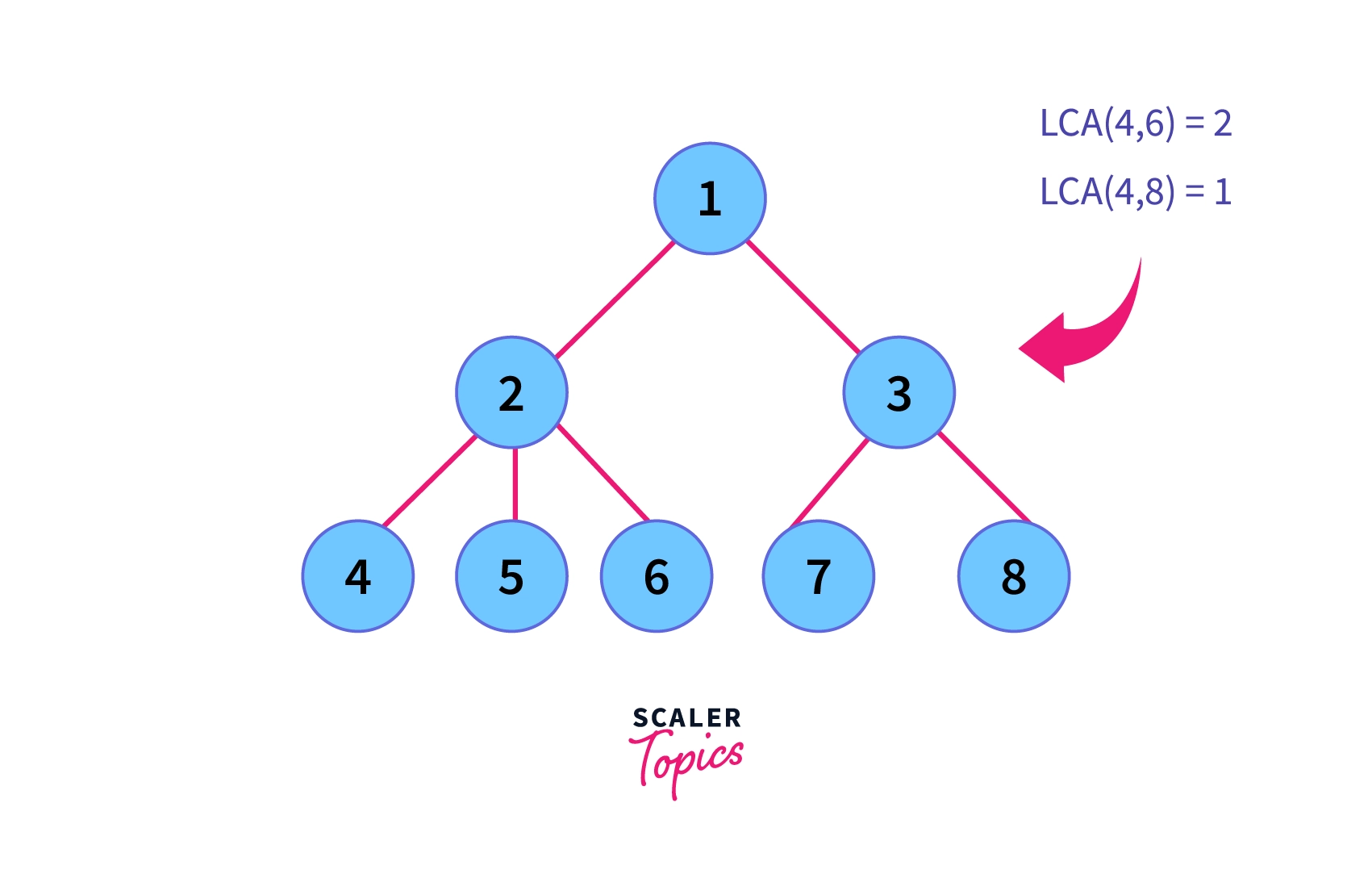
In the above figure, it is clear about the LCA and the next question is that how sparse matrix or sparse table can be used to evaluate it, the idea is to make jumps of powers of two that's called binary jumping/lifting where a sparse matrix is precomputed using depth-first traversal say sparseMatrix[N][l] such that N is the number of nodes in the tree and l is equal to ceil(logN) where the log is to the base 2, in other words, l is the number of intervals in which N can be split as powers of 2.
For example, ceil(log(7)) is 3 because 7 can be broken as i.e., hence, one can make the jumps of these lengths.
The corresponding reccurence for the precomputation of the sparse matrix is sparseMatrix[i][j] = sparseMatrix[sparseMatrix[i][j-1]][j-1] for node i it will compute the parent of i , which has time complexity and for the LCA query say LCA(a,b) for nodes a and b, it will obviously take O(ceil(logN)) because we need to make binary jumps i.e. jumps in which N is splitted.
Conclusion
- We conclude that the sparse matrices which frequently occur in many fields of computer science are mainly represented in more compressed forms.
- Some of those compressed forms are Triplet representation, dictionary of keys (DOK), List of lists (LOL), and Linked list representation.
- These forms are used in order to reduce the space and processing time.
Ready to Build Strong Foundations? Enroll Now in Our Data Structures and Algorithms Course for Coding Excellence!
