Z Algorithm

Overview
Z algorithm is an algorithm for searching a given pattern in a string. It is an efficient algorithm as it has linear time complexity. It has a time complexity of O(m+n), where m is the length of the string and n is the length of the pattern to be searched.
Introduction to Z Algorithm
Ever wondered how to match a pattern in a given string, that too efficiently. For example, if you need to match a DNA sequence with a DNA pattern. DNA sequences have an average length of about 150 billion. Using a brute force string matching algorithm in such a case would lead to very high processing times as it has a quadratic time complexity, making it impractical to be used.
Well, the solution to this problem could be the Z algorithm as it is an efficient string matching algorithm. Read along to know more.
Z algorithm is a pattern searching algorithm. It means that it is used to search for occurrences of a given pattern in a string. It is an efficient algorithm as it has linear time complexity.
What is Z algorithm?
For applying Z algorithm, we require a string and a pattern that is to be searched.
As stated in the previous sections, Z algorithm is an algorithm used for finding occurrences of a pattern in a string. Now let's see how it works.
Z algorithm works by maintaining an auxiliary array called the Z array. This Z array stores the length of the longest substring, starting from the current index, that also it's prefix. This means that each index stores the number of characters, matching the starting characters, starting from this index. This implies that if Z array has a value k for any index, it means that k characters after this index match the first k characters of the string. This is the fundamental part of Z algorithm.
For using Z algorithm, we first concatenate the search pattern and the string to be searched together, adding another character in between, which is not present in any of the strings. Then we generate the Z array for this newly created string.
Then we scan the Z array and at each index where its value is equal to the length of the pattern to be searched, we say that the pattern has been found.
newString=pattern+'$'+string
where $ can be any character not present in either the string or the pattern.
Analysis of Z Algorithm
It's now time to analyse why and how the above-mentioned technique works. Let us first understand the use of the Z array. The Z array, at each index, stores the length of the longest substring starting from it, matching the prefix(starting characters) of the string. Now when we concatenate the pattern to our original string with an additional character, basically we are matching the prefix of the newly created string that is, our pattern, with the rest of the string, that is, our string to be searched.
As we have added an additional character not present in any of our strings, we are sure that a string longer than our pattern will never be found.
Let us understand it with the help of the below example.

As we can see in the example, we have concatenated the pattern and the string with an additional character in between, not present in either of the strings. Now when we generate the Z array, we are basically searching for the first 4 characters of our string, which is also our pattern. As we have added an additional character, the largest pattern that we can find will be the pattern we need to search for. Now, let's analyse the Z array.
The first value of the Z array is explicitly set to zero. As we can see in the array at index 1, as 'a' matches with the character at index 0('a'), the value is set to 1. Then as none of the values are matching, they are set to zero. Now let's see the value at index 10. It is set to 4, as 4 characters starting from this index, match the prefix of the string(starting 4 characters).
Now, to find the occurrence of the pattern, we scan the Z array and we can say that the pattern is found wherever the Z value is equal to the length of the pattern. This is how Z algorithm works.
Working of Z Algorithm
Now let us understand the working of Z algorithm.
First let us understand why Z algorithm uses a window. Z algorithm speeds up its execution by using previous values from the Z array, and these values are used according to the current window. We check that is it possible to have a string greater than the current length inside the current window, and if it is not possible, we skip the calculation for the remaining values inside the window.
This speeds up the algorithm to a great extent as many elements are skipped. If this technique is not used, the algorithm would perform computations for all the elements, and thus get reduced to a quadratic [O()] algorithm, equivalent to naive pattern searching.
Now let us understand how Z algorithm uses a window to speed up its execution. Z algorithm maintains a window between two variables, left and right. While creating the Z array, work is done only inside this window and the window keeps updating. Now while we are inside the window, we find the current elements position inside the window, let it be k.
Then we check the number of elements after k in the window, and if it is greater than the value in the Z array at the kth index, the Z value at the current index becomes equal to the Z value at the kth index.
This is how the window in Z algorithm is used to speed up execution. The window basically uses the already filled values of the Z array.
Algorithm
Z algorithm makes use of the previously scanned part of the string to speed up its execution. We maintain a window [left,right] of matched prefixes and update the window if a mismatch is found.
Steps for maintaining the window are -
- If i > right then there is no prefix substring that starts before i and ends after i, so we reset left and right and compute new [left,right] by comparing str[0..] to str[i..] and get ZArray[i] = (right-left+1).
- If i <= right then let K = i-left, now ZArray[i] >= min(Z[K], right-i+1) because str[i..] matches with str[K..] for atleast right-i+1 characters (they are in [left,right] interval which we know is a prefix substring).
- Now two sub cases arise – a) If ZArray[K] < right-i+1 then there is no prefix substring starting at str[i] (otherwise ZArray[K] would be larger) so ZArray[i] = ZArray[K] and interval [left,right] remains same. b) If ZArray[K] >= right-i+1 then it is possible to extend the [left,right] interval thus we will set left as i and start matching from str[right] onwards and get new right then we will update interval [left,right] and calculate ZArray[i] = (right-left+1).
Dry Run
Lets take a sample String caabxaaab and search for the pattern aab. First thing we will do is to generate a new string by concatenating the old strings. So the new string becomes aab$caabxaaab. Now we will generate the Z array for the this string:
- The value at index zero in the Z array is of no use so it can be left empty, so we start from index 1. Z_Array[1] will be equal to 1 as only one character a matches with the starting character a and b is a mismatch.
- Z_Array[2] will be zero as b is a mismatch with the starting character.
- Z_Array[3] and Z_Array[4] will also be equal to zero as both are mismatches.
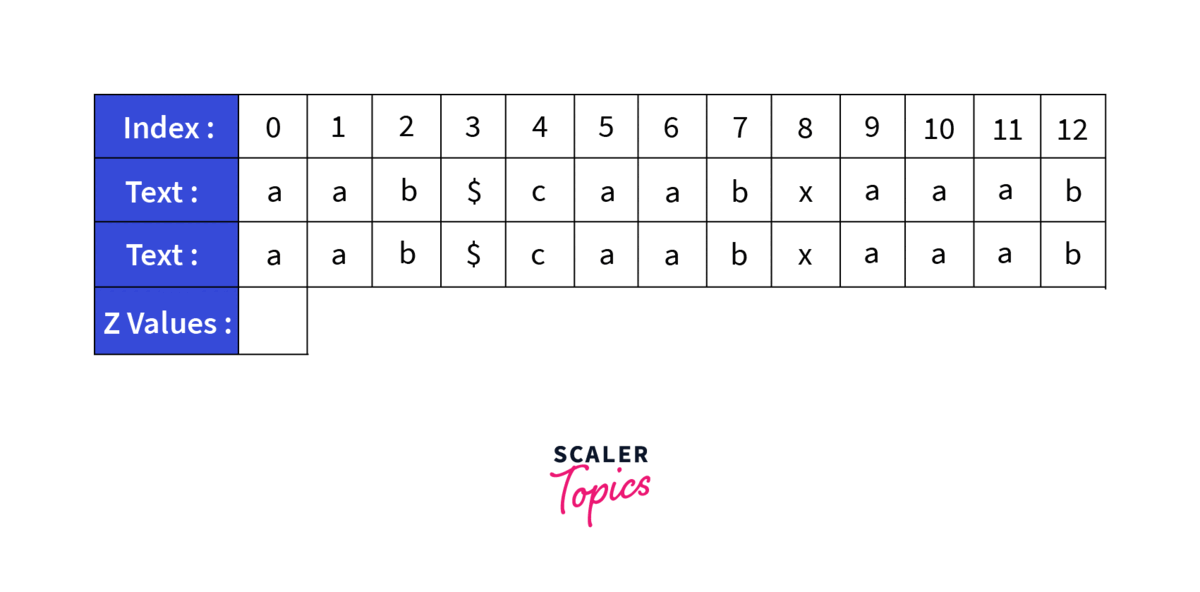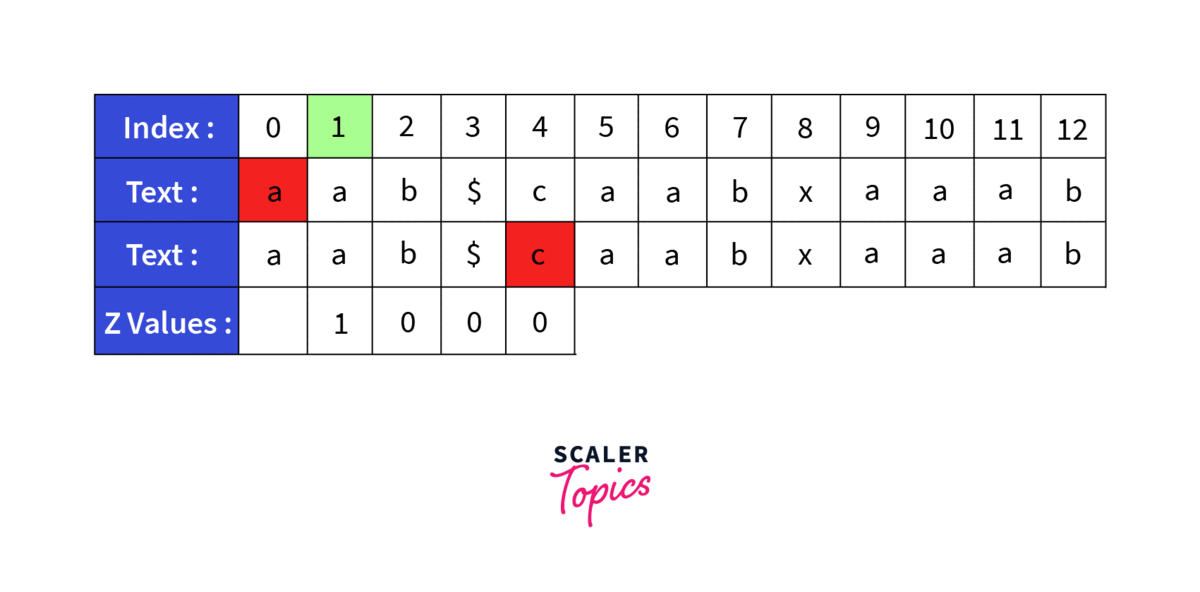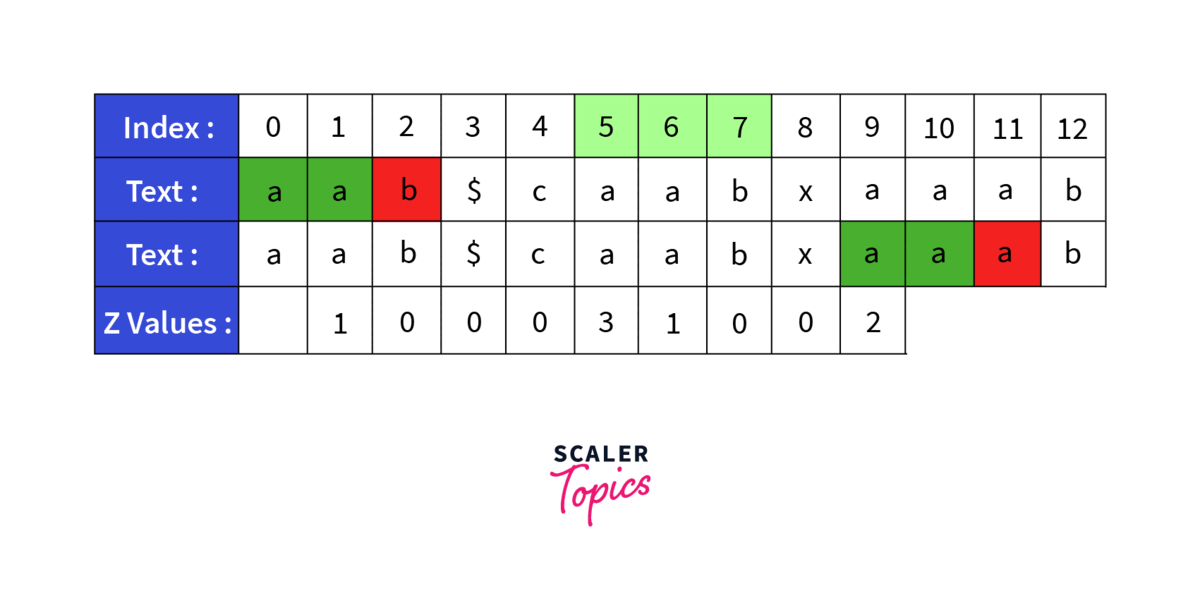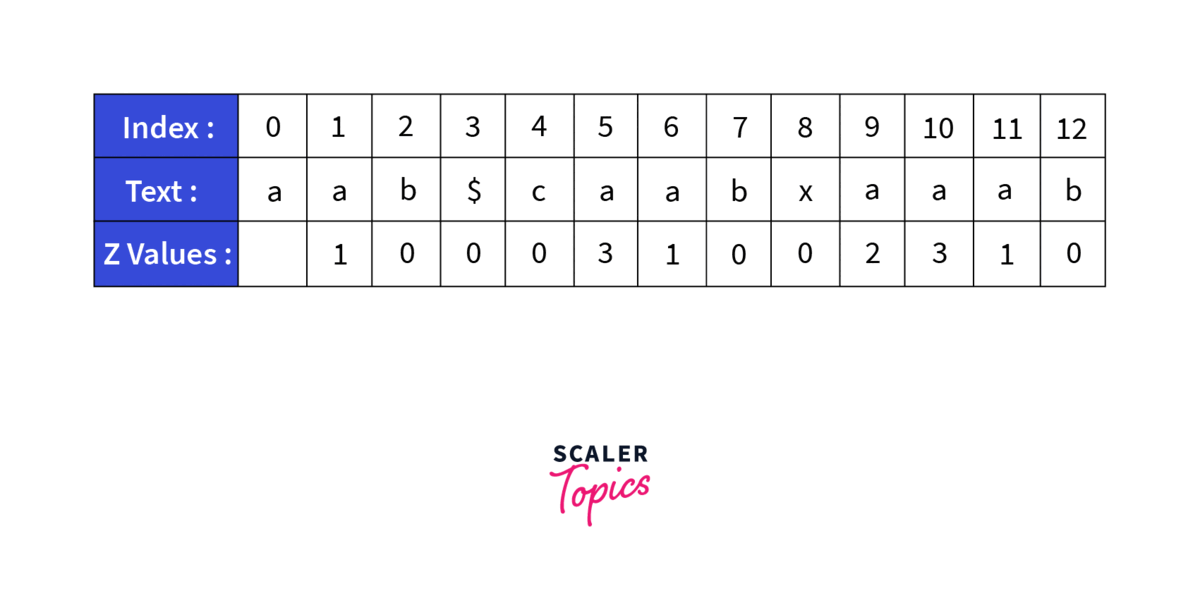
- At Z_Array[5] we find a match, so we compute it explicitly by searching till a mismatch is not found. Z_Array[5] comes out to be 3. So the window becomes [5,7].
- Z_Array[6] is not calculated explicitly as it is inside the window and number of elements after it is greater than Z_Array[1]. So Z_Array[6] becomes equal to Z_Array[1] i.e. 1. Here we have used the previously calculated value.
- Z_Array[7] is also not calculated and previous value of Z_Array[2] is used as value for Z_Array[7].
- Now we come out of the previous window and a new window is created of size 1. Z_Array[8] is computed explicitly and comes out to be 1.
- At Z_Array[9] we find a match, so we compute it explicitly by searching till a mismatch is not found. Z_Array[9] comes out to be 2. So the window becomes [9,11].
- Z_Array[10] is inside the window but the Z value at its position in the window i.e. Z[1] is not less than the number of elements left in the window. So Z_Array[10] is calculated explicitly. It comes out to be 3. The window now becomes [10,12].
- Z_Array[11] is not calculated explicitly as it is inside the window and number of elements after it is greater than Z_Array[1]. So Z_Array[11] becomes equal to Z_Array[1] i.e. 1. Here we have used the previously calculated value.
- Z_Array[12] is also not calculated and previous value of Z_Array[2] is used as value for Z_Array[12].
Final Z array - _ 1 0 0 0 3 1 0 0 2 3 1 0
This is how the Z array is created. We then search for the index with value equal to length of the search pattern and our element is found at that index.
Time Complexity of Z Algorithm
The time complexity of Z algorithm is O(m+n), where n is the length of the string that is searched and m is the length of the pattern that is to be searched for.
It can be calculated as follows: Length of our newly created string is m+n. Traversing the string takes linear time that is = O(m+n)
Whenever a while loop is encountered, lets assume that k number of operations are performed but the next k iterations of the outer loops are skipped as the upper bound is increased by k every time.
So the total time taken for creating Z array remains O(m+n).
Time taken for searching m in the Z array also takes O(m+n) time.
So the total time complexity is:-
- Total time taken for creating Z array remains O(m+n) + Time taken for searching m in the Z array also takes O(m+n) time
=O(m+n)+O(m+n)
=O(m+n)
Implementation of Z Algorithm
-
Z algorithm in C/C++
Output
Explanation Of C++ code
The main function consists of our string and the pattern. Then the find is called with string and pattern as parameters. Now lets see what happens inside find function.
First thing the find function does is to create the string concat by concatenating pattern with string with an additional character $ in between. Now we pass this string concat to the create_Zarr function to create the Z array for this string. Now lets see how the Z array is created.
In the createZarr function, the first thing we do is create two variables called left and right to maintain the search window for creating the array.
Left and right are both initialized to zero. Now we start traversing the string and filling the Z array. The first value of the Z array is never used and can be left unassigned. Now we check if our current pointer i.
If it is greater than right that means we are currently out of the window, so we calculate the Z value at this index using the naive string matching that is by matching each character one by one until a mismatch is found. This value becomes our Z value for the current index.
Now if our current index is currently inside the window i.e., less than right, we calculate k which specifies our current index's position inside the window. If the Z value at kth index is less than right-i+1 i.e., the number of elements inside the window after k, the Z value at the current index becomes equal to the Z value at the kth index and the window will remain the same.
If the Z value at the kth index is greater than or equal to right-i+1, the current window can be extended. So we will set left=i and start matching the string again as done before. After matching the string, our Z value for the current index Z[i] will become equal to right-left.
This is how the Z array will be created for the concat string. Now to find the occurrence of pattern in string we search the Z array for a value equal to the length of pattern and if it is found at index i we can output that the pattern is found at index i-pattern_length-1(removing the extra length added to original string to create Z array).
This is how Z algorithm works to find all occurrences of a pattern in a string.
2. Z algorithm in JAVA
Output
3. Z Algorithm in Python
Output
Examples of Z Algorithm
Z algorithm can be used to find any pattern in a string.
Let's look at some examples.
1. DNA sequence
Z algorithm can be used to find a DNA pattern in a DNA sequence. This application is important as DNA sequences are very large strings and thus an efficient algorithm is required for them.
In this example, we search a DNA sequence of length 100 for the pattern atgc.
Input
Code
Output
2. Word Search
Z Algorithm can also be used to find occurrences of a word in a sentence. In this example, we have found the occurrences of the word the in the sentence.
Input
String=the occurrence of the in this sentence can be found using the Z algo Pattern=the
Code
Output
Applications of Z Algorithm
- Z Algorithm has an important application in finding DNA patterns in a DNA sequence. It is used in this case because Z algorithm works in linear time and as DNA sequences are very large, Z algorithm works efficiently.
- Z algorithm can also be used to find all occurrences of a word in a sentence.
- Z algorithm can be used anywhere to find a pattern in a string.
Z Algortihm vs Others
String matching algorithms comparable to Z algorithm are Rabin-Karp algorithm, KMP algorithm, naive string matching.
Naive String searching algorithm matches the patterns checking it at each and every index whereas Rabin Karp follows a similar approach but it uses a hash function to match the pattern.
KMP algorithm follows a similar approach to Z algorithm but it uses an auxiliary array that stores the longest length of the proper prefix of the pattern that is also a suffix of the pattern.
Time Complexities of String Searching Algorithms
| No. | Algorithm | Best Case | Average Case | Worst Case |
|---|---|---|---|---|
| 1 | Naive String Searching | O(n) | O((n-m+1)*m) | O(n*m) |
| 2 | Rabin Karp | O(n+m) | O(n+m) | O(n*m) |
| 3 | KMP | O(n+m) | O(n+m) | O(n+m) |
| 4 | Z Algorithm | O(n+m) | O(n+m) | O(n+m) |
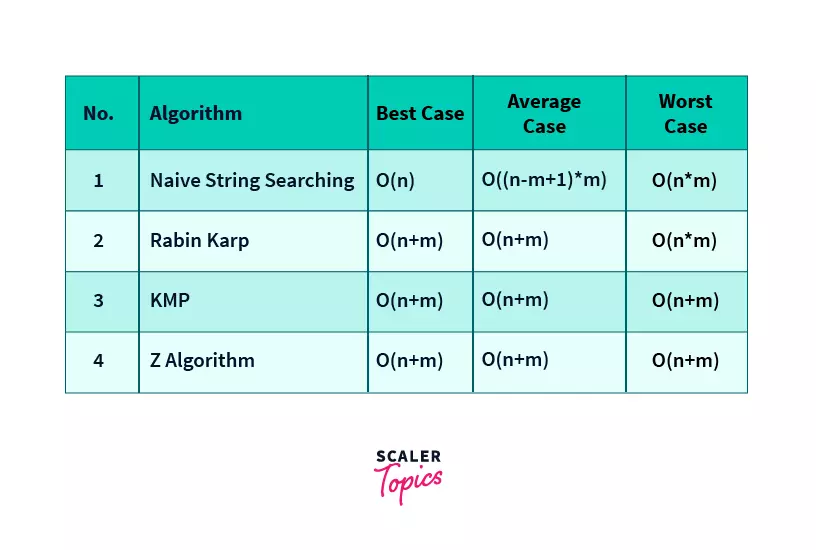
Here n is the length of the String in which the pattern is to be searched and m is the length of the pattern that is to be searched.
In the above tables, we can see that naive string matching and Rabin Karp algorithms have very high time complexities and thus their use should be avoided for big inputs.
KMP algorithm and Z algorithm have similar time complexities and can be used interchangeably but the use of Z algorithm should be preferred as it is easier to code and understand and even debugging the Z array is easier than debugging the auxiliary array in KMP.
Conclusion
- In this article, first, we have seen the basic working of Z algorithm.
- After that we came to an example to better understand the working of Z algorithm.
- Then we have also studied how to write code for Z algorithm with the help of the pseudocode/algorithm.
- That is followed by a time complexity analysis of Z algorithm.
- After that we have also implemented Z algorithm in C++ with explanation and have also implemented Z algorithm in JAVA and Python.
- Finally discussed applications and examples of Z algorithm and also compared Z algorithm to algorithms similar to it.
