Diagonal Traversal of Binary Tree

Problem Statement

Given a binary tree $A$ containing $n$ nodes, consider diagonals (lines with a slope of $-1$ ) passing between the nodes and print all the diagonal elements in the binary tree belonging to the same line.

Note: The diagonals with a slope of $-45\text{ degree}$ angle, will be like a $\backslash$ .

This question has been asked in interviews with Amazon and DE Shaw.

To understand this question better, look at the examples in the below sections.

Example 1

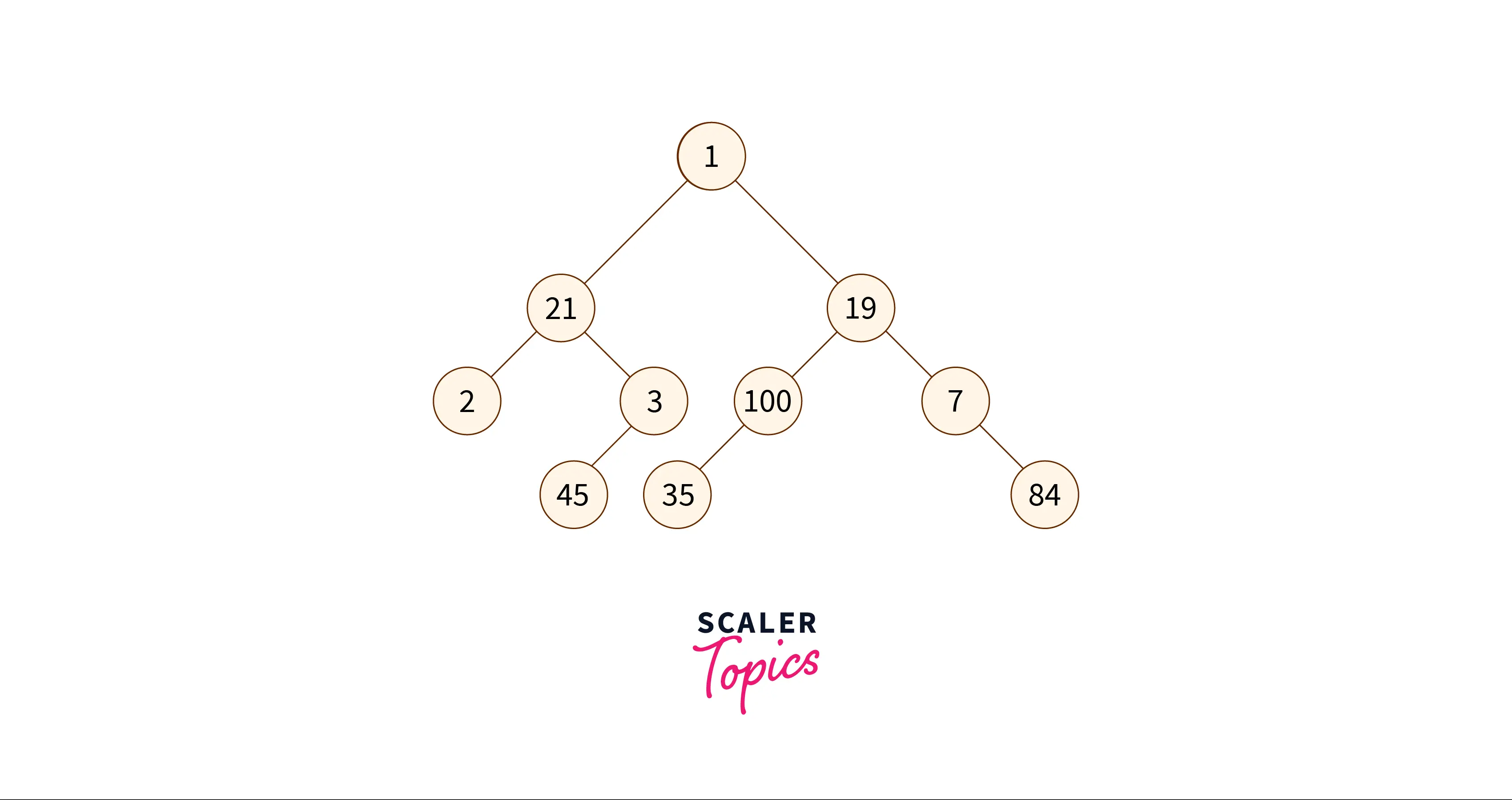
Input

Output

Explanation

The diagonal traversal of the given tree is:

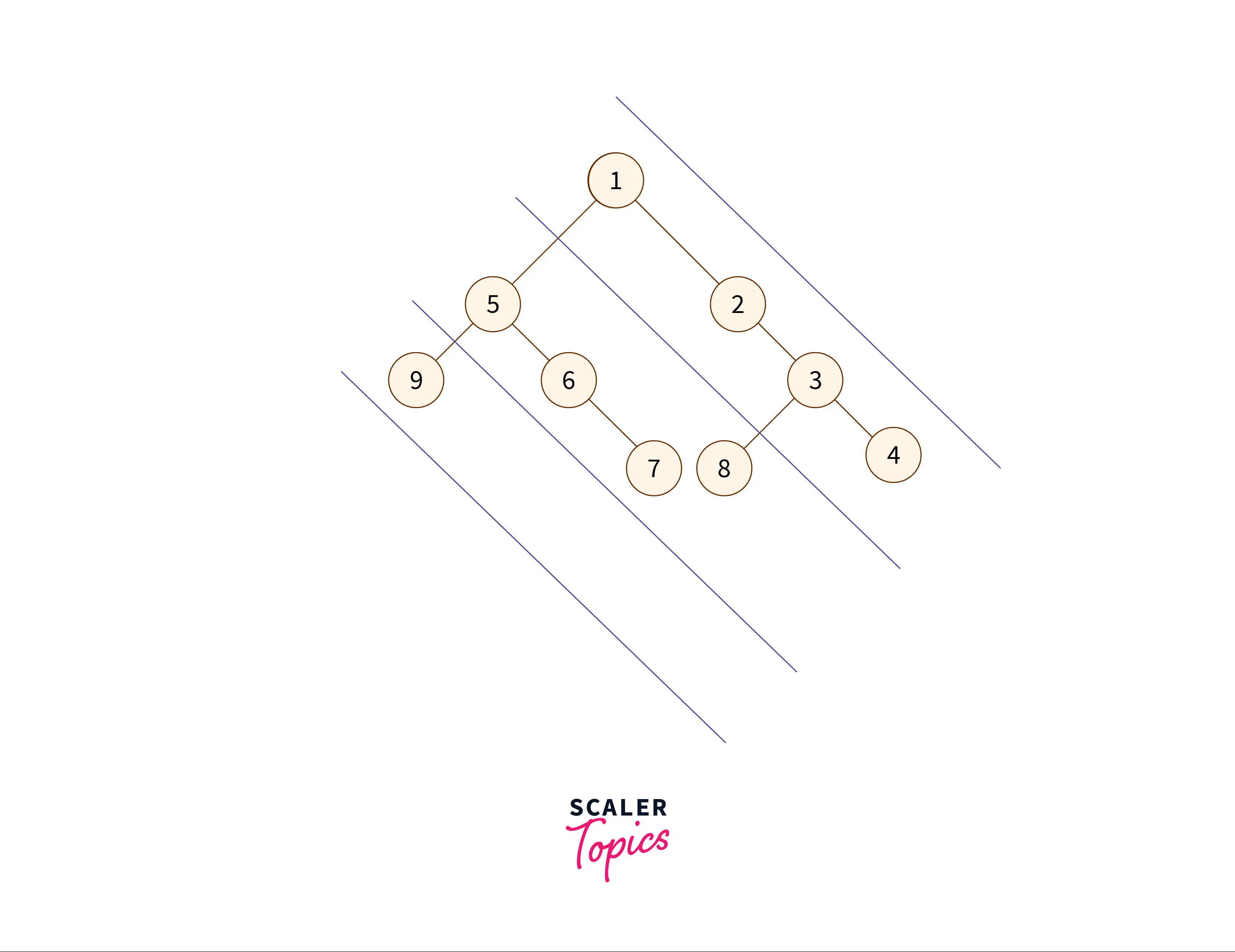
diagonal-element-of-first-binary-tree

As we can see in the above image, the red lines are the diagonals of the binary tree, and the nodes between them are diagonal nodes. Printing them in the diagonal fashion will result in this order: $1, 2, 3, 4, 5, 6, 7, 8, 9$ .

Example 2

Input

Output

Explanation

The diagonal traversal of the given tree is:

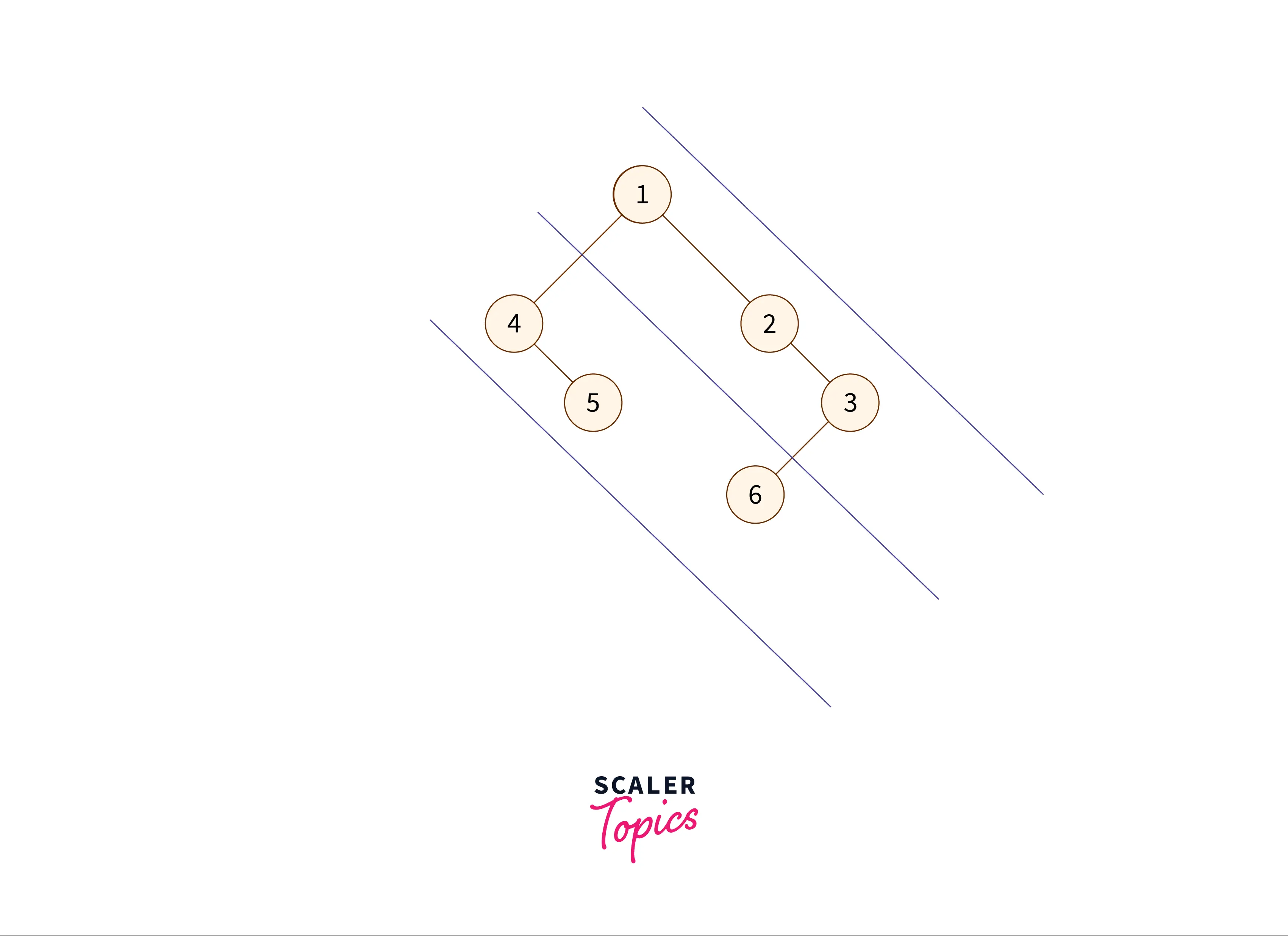
diagonal-element-of-second-binary-tree

Constraints

$0 \leq n \leq 10 ^ 5$

The number of nodes in the binary tree should be less than $10 ^ 5$ .

Algorithm 1 - Recursive Approach (Hashing)

In this recursive approach, we will use hashing. The idea is to create an empty hashtable diagonalPrint, where each key in the map represents a diagonal in the binary tree (numbering from 0), and its value is a list that contains all the nodes present in the diagonal in sequential order. We will then perform preorder traversal on the tree to update the map. For each node, recur for its left subtree by increasing the diagonal d by one and recur for the right subtree with the same diagonal d.

Steps of the Algorithm

Steps inside the diagonalTraversal() function:

Initialize an array list ans. (To store the answer, i.e., the diagonal elements of the binary tree)
Initialize a hashtable diagonalPrint. (To store the diagonal no. as key and the list of elements in that diagonal as a value)
Calling the diagonalTraversalUtil() function by passing $root$ of the binary tree, 0 (first diagonal no.), and diagonalPrint hashtable. (diagonalTraversalUtil() is a recursive function used to get the diagonal elements of the binary tree)
Copy the values inside the array list of the hashtable to the ans array list.
Return the array list ans. (Returning the array list ans which contains all the diagonal elements of the given binary tree in sequence)

Steps inside the diagonalTraversalUtil() function:

Check if the $node$ is NULL, if yes, return. (Base case)
Insert the diagonal's elements into the $dth$ list of the hashmap. (Adding the elements of the same diagonal)
Recursively call the function diagonalTraversalUtil() by passing $node \longrightarrow left, d + 1$ , and the hashtable diagonalPrint. (To move to another diagonal by incrementing $d$ by $1$ )
Recursively call the function diagonalTraversalUtil() by passing $node \longrightarrow right, d$ , and the hashtable diagonalPrint. (To move to another element of the same diagonal)

Implementation (in C++ 20, Java SE 18, and Python 3)

Implementing the recursive approach to print the diagonal elements of a given binary tree in C++, Java, and Python.

C++ 20 Implementation

Java SE 18 Implementation

Python 3 Implementation

Output

Explanation

In this algorithm, we are passing the root of the binary tree to the diagonalTraversal() function, which calls the recursive function diagonalTraversalUtil(). The $diagonalTraversalUtil()$ function adds the diagonal elements into the hashmap in which key is the no. of the diagonal and the value is the list of elements in that diagonal.

The diagonal traversal of the given tree is:

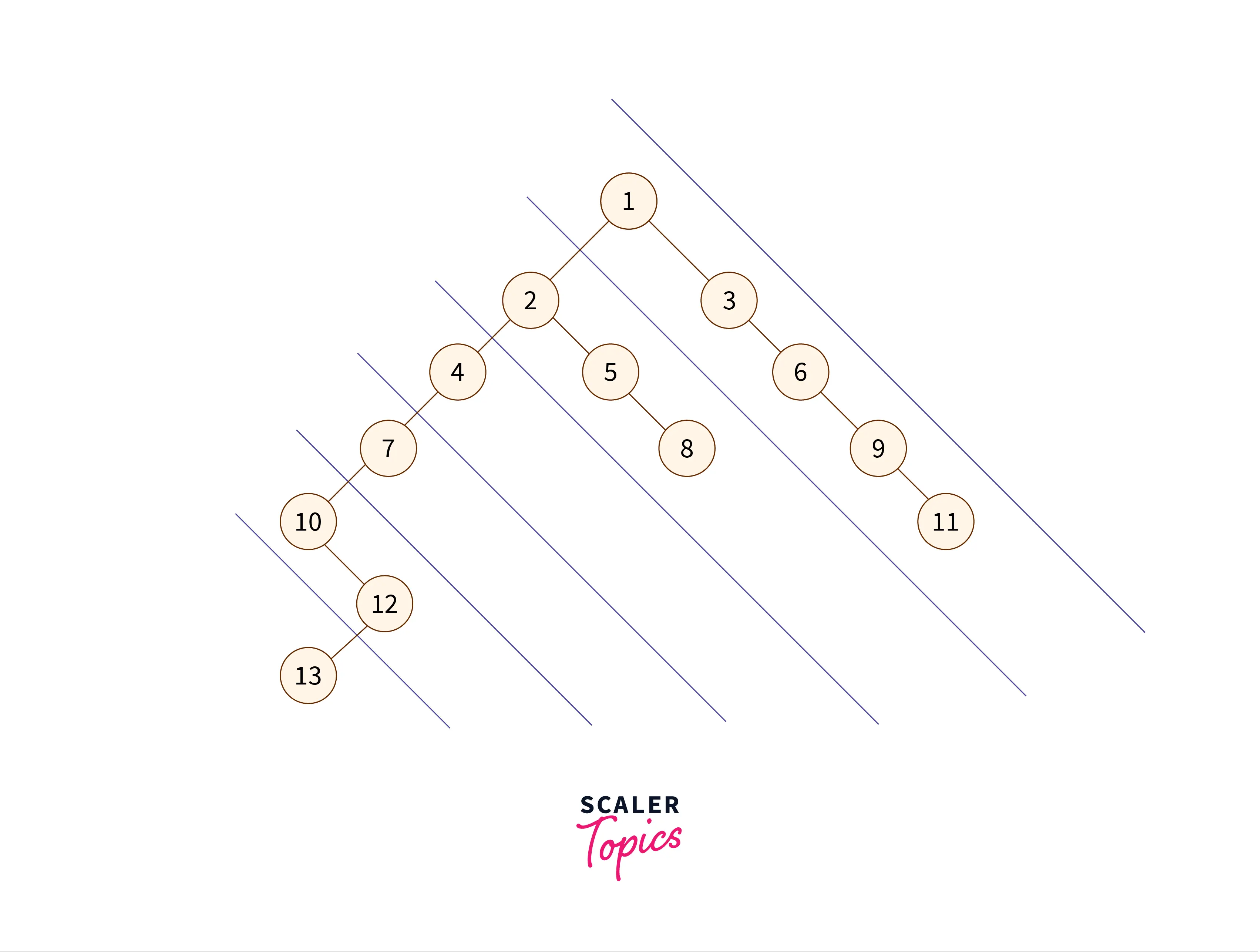
diagonal-traversal-of-first-input

Complexity Analysis

Time Complexity: O(n) We are visiting each node in the binary tree once, so the time complexity of this algorithm will be $O (n)$ .

Space Complexity: O(n) A hashmap is used to store the no. of diagonals and elements in diagonals using a list, therefore, the total space taken by the hashmap will be $O (n)$ . Therefore, the space complexity of the algorithm will be O(n).

Algorithm 2 - Iterative Approach (Using Queue)

In this iterative approach, we will use a Queue data structure. The idea is similar to level order traversal (Breadth first traversal), but instead of storing nodes of a level, we enqueue nodes (add nodes at the back of the queue) in a diagonal and visit them later.

Steps of the Algorithm

Initialize an array list $ans$ . (To store the answer, i.e., the diagonal elements of the binary tree)
Initialize a queue $q$ . (To store the $left$ nodes of the binary tree)
Check if the $root$ is NULL, if yes, return $ans$ . (Edge case)
Enqueue $root$ into the queue $q$ . (The $root$ is the part of the first diagonal line)
Run a while loop till $q$ gets empty. (If $q$ gets empty, we have reached the end of the given binary tree)
Inside the while loop, initialize a TreeNode object $temp$ and assign it to the front of the queue, and then pop the front element of the queue $q$ . (To move to the other diagonal)
Run a nested while loop till $temp$ becomes $NULL$ . (If $temp$ is NULL, we have reached the end of the present diagonal line)
Inside the nested while loop, check if $temp \longrightarrow left$ exists, if yes, enqueue it inside the queue $q$ . Then add the element $temp \longrightarrow data$ inside the array list $ans$ and then assign $temp$ to be $temp \longrightarrow right$ . (To store the left node in the queue $q$ , add the data element inside the $ans$ array, and then move to the right node)
Return the array list $ans$ . (Returning the array list $ans$ which contains all the diagonal elements of the given binary tree in sequence)

Implementation (in C++ 20, Java SE 18, and Python 3)

Implementing the iterative approach to print the diagonal elements of a given binary tree in C++, Java, and Python.

C++ 20 Implementation

Java SE 18 Implementation

Python 3 Implementation

Output

The output for all these implementations will be the same as the algorithm and the binary tree used are the same.

Explanation

In this algorithm, we are passing the root of the binary tree to the $diagonalTraversal()$ function, which uses the iterative method with the help of a queue to get the diagonal elements of the given binary tree. The queue is used to store the left nodes of the binary tree (as left nodes create a new diagonal) so that we can visit them later and carry on with adding the elements of the right node (elements of the same diagonal) to the answer array/list $ans$ .

The diagonal traversal of the given tree is:

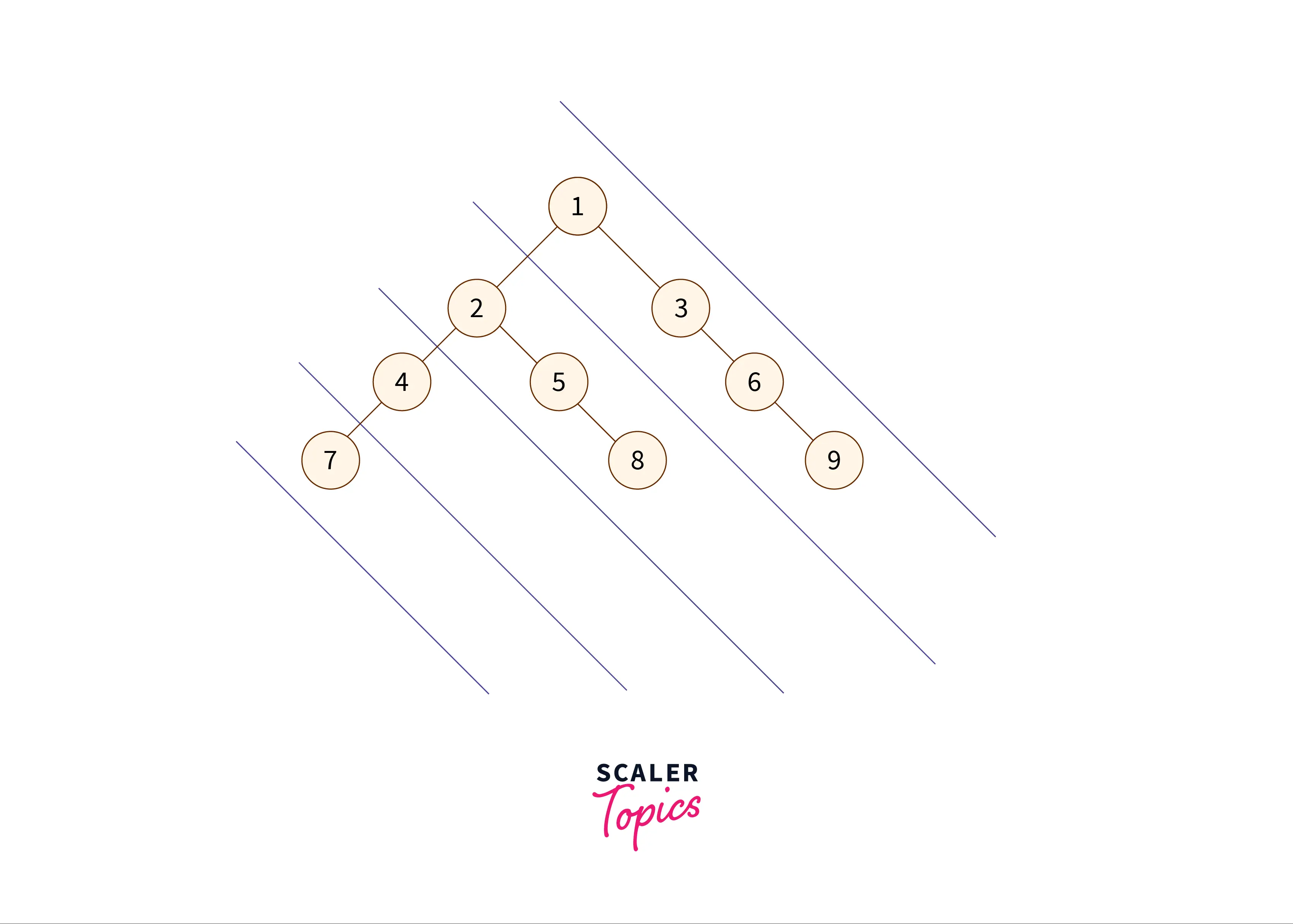
diagonal-traversal-of-second-input

Complexity Analysis

Time Complexity: O(n)
It may look like the time complexity for this algorithm will be $O (n ^ 2)$ as there is a nested while loop inside another one, but we are visiting all the nodes at maximum twice (adding and removing them from the queue) so the time complexity will be $O (n)$ .

Space Complexity: O(n)
The space complexity will be the number of diagonals of left nodes in the binary tree as we are using a queue to store them, but in the worst case, assuming there are only left nodes in the binary tree, the space of the queue will be $n$ . Therefore, the space complexity of this algorithm will be $O (n)$ .

Conclusion

The problem statement is to print the elements between each diagonal (consider lines of slope $-1$ ) passing between the nodes of the binary tree.
We can solve this problem using the recursive approach with the help of a hashtable.
The time and space complexity of the recursive approach is $O (n)$ .
We can also solve this problem using the iterative approach with the help of a queue data structure.
The time and space complexity of the iterative approach is $O (n)$ .

FAQ

Q.What is a Hashtable?

A. A Hashtable is a data structure that stores elements in key-value pairs where keys are used for accessing the values.
They are generally unordered and are called HashMap in Java, unordered_map in C++, and dictionary in Python. An ordered Hashtable is called a map in C++ and OrderedDict in Python.

To learn more about Hashing and Hashtables, click here.

Q.What is a Queue Data Structure?

A. A Queue is a linear data structure that follows the FIFO (First In First Out) order. The deletion of an element is done from the front of the queue and the insertion of an element is done at the back of the queue. A real example of a queue data structure is a queue of people to buy movie tickets, people will join back the queue from the back and leave the queue from the front.

To learn more about the Queue data structure, click here.

Q.What is Recursion?

A. Recursion is a process in which a function calls itself directly or indirectly. The function that calls itself is called a recursive function. Recursion is used for many problems like Tree traversal (like we just did in this article), Depth-First search of a Graph, Tower of Hanoi, etc.

To learn more about recursion as well as learn about backtracking, click here.

Q.What is a Binary Tree?

A. A Binary Tree is a tree data structure in which each node has at most two children nodes, which are referred to as the left child node and the right child node. An empty tree is also considered a valid Binary Tree.

To learn more about Binary Trees, click here.

Q.What are Different Possible Traversals for Binary Trees?

A. The different possible ways of traversal of a Binary Tree are: Depth First Traversal (In-order, Pre-order, and Post-order), Breadth First Traversal, and Diagonal Traversal (Positive and Negative Slope).

Let us understand this using an example:

representation-of-binary-tree

Pre-order Traversal: $1, 21, 2, 3, 45, 19, 100, 35, 7, 84$ In-order Traversal: $2, 21, 45, 3, 1, 35, 100, 19, 7, 84$ Post-order Traversal: $2, 45, 3, 21, 35, 100, 84, 7, 19, 1$ Bread First Traversal: $1, 21, 19, 2, 3, 100, 7, 45, 35, 84$ Positive Slope Diagonal Traversal: $1, 19, 7, 84, 21, 3, 100, 2, 45, 35$ Negative Slope Diagonal Traversal: $1, 21, 2, 19, 100, 35, 3, 45, 7, 84$

To learn more about traversal of Binary Tree, click here.

Q.What if the Slope of the Diagonals were 1 and not -1?

A. If the slope of the diagonal was 1 instead of -1, the diagonals on the binary tree will look like this,

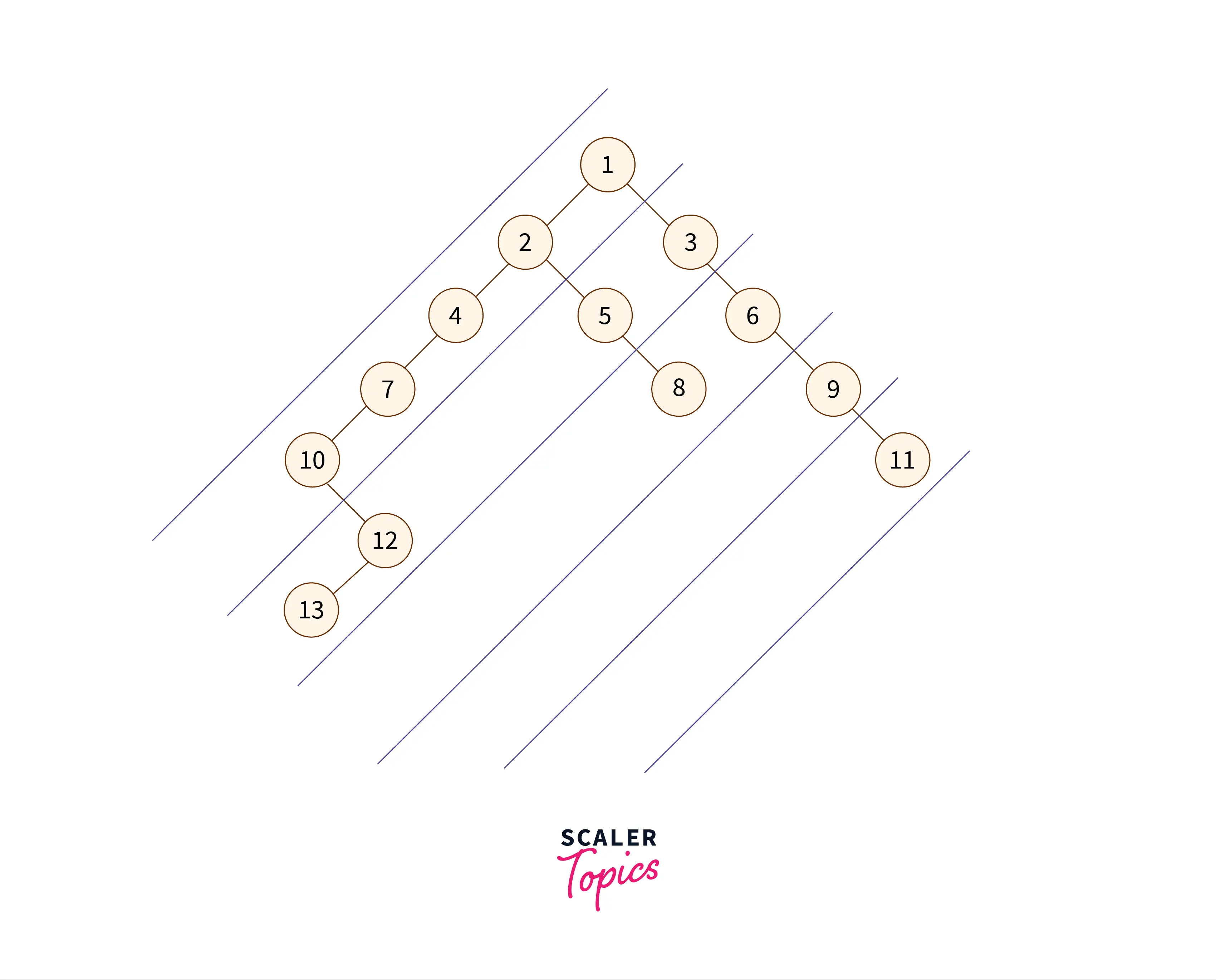
slope-of-diagonal-is-minus1

In the above image, the negative slope diagonal traversal of the binary tree above will be $1, 2, 4, 7, 10, 3, 5, 12, 13, 6, 8, 9, 11$ .

To change the given code in this article for diagonal of slope $1$ , just replace the $left$ node with the $right$ node and vice-versa.