Min Stack Problem

The Min Stack problem is designing a stack data structure such that, along with the good old stack operations push(), pop(), peek(), isEmpty(), etc., there should be one additional method called getMin() that returns a minimum element present in the stack. All these stack methods should be performed in constant time, i.e., O(1) time complexity. This question was asked in interviews with companies like Amazon, Adobe, LinkedIn, Paytm, etc.
We can create a single variable to store the minimum value, but the problem with that approach is that if the minimum element is popped, then we will have to traverse the stack to get the new minimum element. This will make the pop operation's time complexity . Let us look at the approaches that facilitate all the operations with time complexity.
Problem Statement
Design and implement a special stack data structure that supports normal stack operations, namely, push, pop, top, isEmpty, size, and the special operation getMin. All the operations must be performed at a constant time complexity of .
- void push(int x):
Inserts element x to the stack. - int pop():
Removes the element at the top and returns it. - int top():
Returns the element at the top of the stack. - bool isEmpty():
Returns true if the size of the Stack is 0, else returns false. - getMin():
Returns the minimum element currently present in the stack. It may or may not be at the top.
Note:
In some cases, we are required to use only the standard stack given in language implementation. We are not supposed to use any other data structure, like an array or linked list, for special stack implementation.
Example
Example - 1
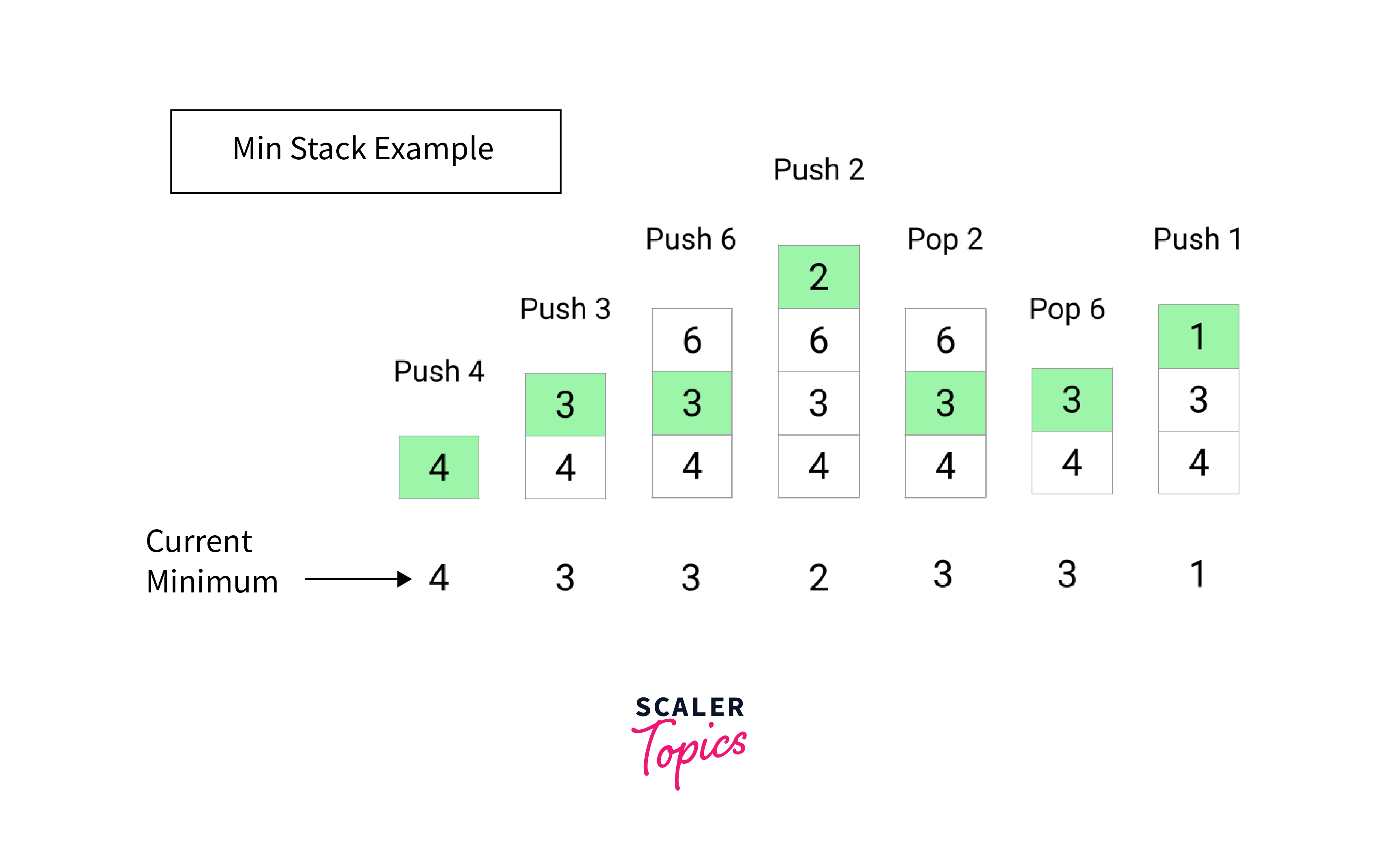
Example - 2
| push 3 | push 5 | push 2 | push 1 | getMin() | pop | pop | getMIn |
|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||
| 2 | 2 | 2 | 2 | ||||
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| MIN - 3 | MIN - 3 | MIN - 2 | MIN - 1 | MIN - 1 | MIN - 2 | MIN - 3 | MIN - 3 |
Approach - 1: Using Two Stacks
We will use two stacks, the minStack and the mainStack. The idea is simple, if the current element is less than the top element of minStack push the current element to the minStack.
Each time a user retrieves a min element, we can compare it to the top element in both the stacks and return the minimum. If an element is popped from the mainStack then we will check if the same element is at the top of the minStack if so we will have to pop from there as well.
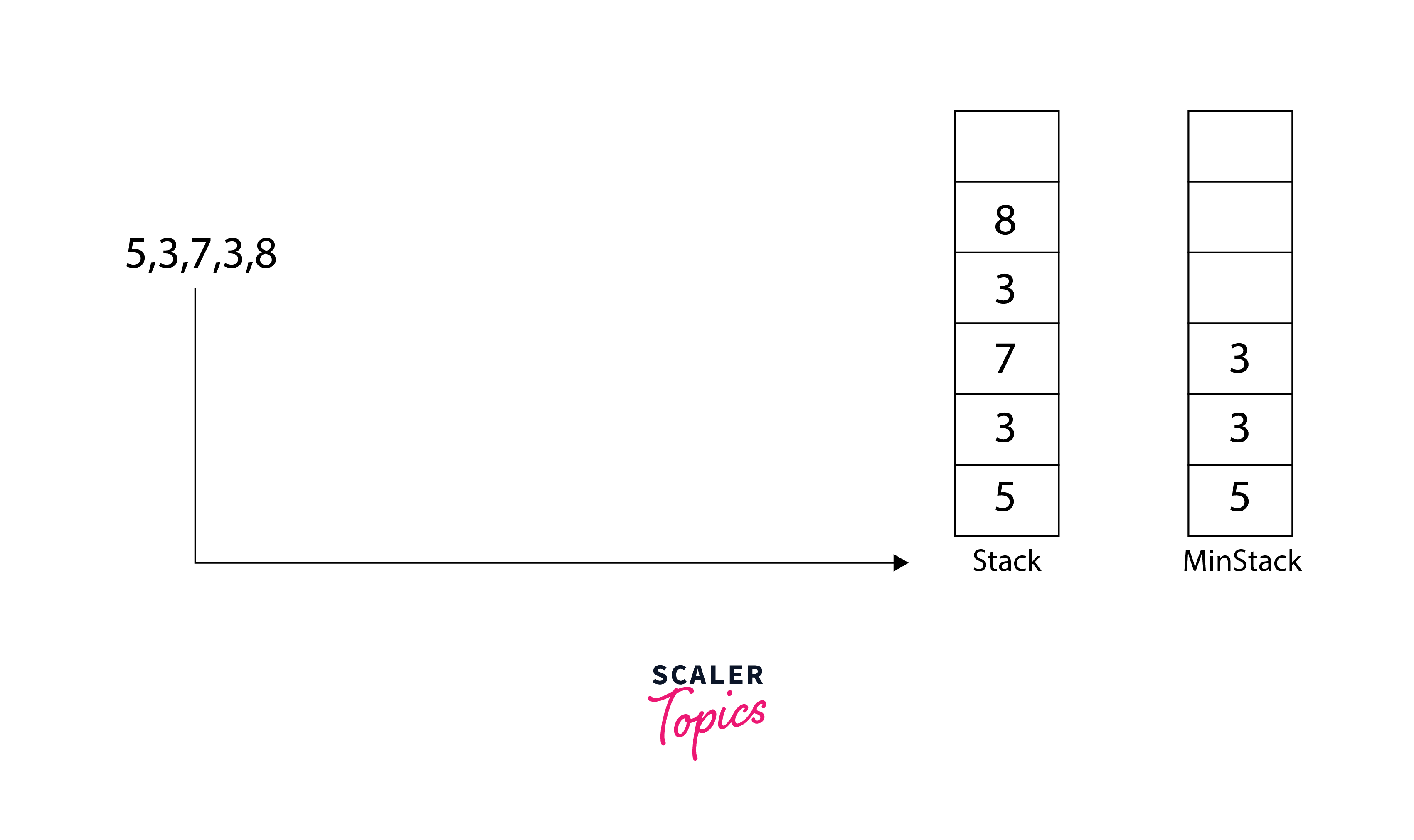
Illustration
- push():
- Simply, push to the mainStack.
- Check if the minStack is empty, if so push the current element. Else, check if minStack.top() <= current push current element in the stack.
- pop():
- Pop the value from the mainStack. Check if popedCurrent == minStack.top() pop the value from the minStack() as well.
- getMin():
- Get the minimum from the top of minStack.top().
Implementation
C:
CPP:
JAVA:
PYTHON:
Output:
Complexity Analysis
All the operations are performed in constant time complexity as we are not using any sorting or searching techniques. An additional space is occupied by the minStack.
- Time Complexity:
- Space Complexity: where is the number of elements in the mainStack.
This approach ensures that the minimum element is efficiently tracked and can be retrieved in constant time without the need to search the entire stack. This approach satisfies the problem requirements, the only catch is it uses an extra stack.
Approach - 2: Using One Stack
We can do the same operation without using any additional space. This can be achieved with the help of some additional mathematical calculations.
We will use only an extra int variable called minVal to store the current minimum value.
- stackTopValue: is the value currently stored in the stack at the top.
- newMinValue: After the push or pop operations, the change in the minValue.
- oldMinValue: minValue before the operation. With the help of oldMinValue, we will be calculating stackTopValue and newMinValue.
Now, for the very first element when the stack is empty, we initialize the minVal with the current value and push the element to the stack.
If the minVal is already less than the current value, we simply push the current value to the stack as popping this value will not affect minVal.
Complexity arises when the value lesser than minVal is pushed to the stack. In this case, if we update the minVal with the new value, then popping this will require stack traversal for the calculation of the minVal.
In this approach, the following formula is used:
newMinValue is the current element, oldMinValue is the previous element, and the value to be pushed to the stack is the stackTopVlaue.
We know that oldMinValue <= newMinValue and therefore, stackTopValue <= newMinValue:
So, if the minValue changes, we will push a number that is less than or equal to the newMinValue and then change the value of minVal with the current element. This will indicate that the new minimum was introduced at this point and calculation must be performed to derive the original value as well as oldMinValue if top() or pop() operations are performed.
Multiplying the minValue with 2 ensures that for negative numbers as well we will get a smaller value for stackTopValue. Say, for example oldMinValue = -1 and newMinValue = -2, stackTopValue = -4 - (-1) = -3.
For the top() operation we will check if the stackTopValue <= minValue. In this case, we know that a newMinValue was introduced and is stored in minVal. So we will simply return minVal. Otherwise, we can return the top() as it is as math transformation was not performed.
When the pop() operation is performed if the minVal < stackTopValue, no change was made and thus we can remove the value and return it. Otherwise, we will have to calculate the oldMinValue. This can be calculated by reversing the previously used formula:
We will return the minVal's value in pop operation.
Illustration
- push():
- If the stack is empty, push the current element to the stack. Update the minVal with the current value.
- Else if the current >= minVal, push the current to the stack.
- Else
- push 2 * current - minVal to the stack.
- pop():
- If the mainStack.top() < minValue then update minVal = 2 * mainStack.top() - minVal and return previously store minVal.
- Else pop the element from the stack and return it.
- top():
- If mainStack.top() < minValue, return minValue.
- else return the mainStack.top().
- getMin():
- return minValue.
Let's dry-run the one-stack solution with mathematical transformation:
Initial Stack: Empty
Operation: push(3)
- Transformation: As it's the first element, directly push 3.
- Stack: [3]
- Minimum Value: 3
Operation: push(5)
- Transformation: 5 > 3, so directly push 5.
- Stack: [3, 5]
- Minimum Value: 3
Operation: push(2)
- Transformation: 2 < 3, so push 2 * 2 - 3 = 1.
- Stack: [3, 5, 1]
- Minimum Value: 2 (represented internally by 1)
Operation: push(1)
- Transformation: 1 < 2, so push 2 * 1 - 2 = 0.
- Stack: [3, 5, 1, 0]
- Minimum Value: 1 (represented internally by 0)
Operation: getMin()
- Returns the current minimum value (represented internally): 0, which translates to 1.
Operation: pop()
- Pops the top element (0).
- As 0 represents the minimum value, the actual minimum is 2.
- Decrement current minimum by multiplying the popped value with 2: 2 * 0 - 2 = -2.
- Update the minimum value: 2 -> -2 (represented internally).
- Stack: [3, 5, 1]
- Minimum Value: 2 (represented internally by -2)
Operation: getMin()
- Returns the current minimum value (represented internally): -2, which translates to 2.
Implementation
C:
CPP:
JAVA:
PYTHON:
Output:
Complexity Analysis
This is the most optimal approach. It performs all the operations in time complexity. With mathematical calculations performed in constant time, we can also reduce space complexity to constant.
- Time Complexity:
- Space Complexity:
Approach - 3: Using Linked List Implementation of the Stack
In this approach, we can either use a LinkedList or a Stack. This is the simplest approach, rather than storing a single element, we will store the minimum and current both in the Stack. This can be done by using an int array of fixed size 2 or a std::pair in CPP.
Illustration
- push():
- Check if the current <= mainStack.top()[1] or the stack is empty, push a new int array such that, arr[0] = arr[1] = current.
- Else store the mainStack.top()[1] in the variable temp and insert new int[]{current, temp} in the stack.
- pop():
- Pop the top element from the Stack or LinkedList return the main value and discard the minValue.
- getMin():
- Get the minimum from the top of mainStack.top()[1].
Implementation
C
CPP
JAVA
PYTHON
Output:
Complexity Analysis
This simple method performs all the operations in time complexity. It only uses an additional space by storing minValue for each element pushed to the Stack thus being the least efficient method of all.
- Time Complexity:
- Space Complexity:
Conclusion
- Min Stack requires implementation of a special stack that performs push, pop, and top, operations and a special function getMin() in time complexity.
- The first approach uses two stacks to store the minimum values. If the current value is less than the top of the stack we push this value to the minsTack.
- The second approach uses mathematical transformation. This reduces space complexity to . This is the most optimal approach.
- The LinkedList approach encourages us to store the minValue with each value inserted. This is very simple but helpful logic if space complexity is not an issue. Learn more on data structure
