Constraint Satisfaction in NLP

Introduction

Consider a Sudoku puzzle in which some numbers are initially entered into some squares. You must complete the vacant squares with numbers ranging from 1 to 9 so that no row, column, or block has the same number twice. This is a fundamental constraint satisfaction problem. You must solve an issue while keeping certain limits in mind. The remaining squares to be filled are referred to as variables, and the range of values $(1-9)$ that can fill them is referred to as a domain. Variables are assigned domain values.

Constraints are the conditions that determine how a variable chooses its domain.

The approaches employed in constraint satisfaction are determined by the type of constraints evaluated. Constraints on a finite domain are frequently employed to the point that constraint satisfaction problems are typically identified with problems based on constraints on a limited domain. Such issues are typically resolved by search, specifically through backtracking or local search. Other approaches employed on such issues include constraint propagation; however, most of them still need to be completed in that they may solve or prove the problem unsatisfiable, but not always.

Let's define it formally.

What is the Constraint Satisfaction Problem?

A constraint satisfaction problem (CSP) must be solved within certain limitations or criteria, commonly known as constraints. It is made up of the following components:

• The solution is stored in a finite set of variables $(V = V1, V2, V3,....., Vn)$.
• The domain is a set of discrete values from which the solution is chosen $(D = D1, D2, D3,....., Dn)$.
• A limited number of restrictions or constraints $(C = C1, C2, C3,......, Cn)$.

How to Solve Constraint Satisfaction in NLP?

The requirements to solve a constraint satisfaction problem are:

• a state space
• a notion of the solution.

A state, in a state space, is defined by assigning values to some, or all of the variables such as - X₁ = v₁, X₂ = v₂ and so on.

In a constraint satisfaction problem, an assignment of values to a variable can be done in three ways:

• Consistent or Legal Assignment:
  An assignment that does not violate any constraint or rule is called a Consistent or legal assignment.
• Complete Assignment:
  An assignment where every variable is assigned with a value, and the solution to the CSP remains consistent is known as a Complete assignment.
• Partial Assignment:
  This assignment assigns values to some of the variables only.

To solve constraint satisfaction problems, our first thought is to "search" for the right solution or the right inputs that satisfy the constraints as well as help us reach the solution. Hence, to solve constraint satisfaction problems, we can make use of different search algorithms, such as the following.

Before we get to the algorithms for search in constraint satisfaction problems, why are these problems not just like classical search problems? There are two main differences.

First, a constraint satisfaction problem does not care what order the variables are placed in. When completing a Sudoku puzzle, for instance, it is irrelevant whether we initially set $S[1,9]$ or $S[9,1]$. On the other hand, the order does matter when attempting to find the quickest route between two places on a map. Before going from B to C, we must first get from point A to point B. Therefore, a constraint satisfaction problem solution is a set of assignments that we can make in any order, as opposed to a solution to a classical search issue, which is an ordered sequence of activities.

The second difference is that, from the perspective of the algorithms, the solutions in classical search are atomic. They evaluate solutions using the goal test and cost function, but they don't look inside them. The algorithms used to solve constraint satisfaction problems, on the other hand, are aware of each variable that contributes to the solution and set them one at a time.

Now, moving on to two of the searches that can be used to solve a constraint satisfaction problem.

Generate and Test Algorithm

Have you ever heard about brute force hacking attacks? The same idea applies here. This method enables you to create a full assignment for each variable, determine whether that assignment is a solution, and determine whether each constraint has been met. If so, this approach has succeeded; if not, start over. There is a lot of pointless effort, thus this is not the ideal approach. Instead, let's come up with a more clever solution.

Backtracking Search

Backtracking search is a form of depth-first search which chooses values for one variable at a time and then backtracks when a variable has no legal values (values within constraints) left to assign and has not reached the solution. These algorithms repeatedly choose an unassigned variable and try all values in the domain of that variable to find the correct solution. If an inconsistency is detected while finding the solution, then these algorithms return a failure causing the algorithm to "backtrack" to try another value.

Backtracking searches keep only a single representation of a state and alter those representations instead of creating new ones.

Local Search

Local searches for constraint satisfaction problems, uses a complete state formulation. Here, the initial state assigns a value to every variable, and the search changes the value of one variable at a time. While choosing a new value of variables, local search selects the value that results in the minimum number of conflicts with other variables.

Types of Domains in the Constraint Satisfaction Problems

The variables in constraint satisfaction problems employ the following two types of domains:

Discrete Domain:
A discrete domain is an infinite domain with only one state for several variables. For example, each variable can have an endless number of start states.

Finite Domain:
A Finite domain has continuous states that describe one domain for one specific variable. It's also known as a continuous domain.

Until now, we have been looking at constraint satisfaction problems from a very broad perspective or the perspective of artificial intelligence. Natural Language Processing can also be viewed as a constraint satisfaction problem. Let us take a look at the four basic types of constraints in NLP, as well as the constraints concerning variables.

Constraint Types in CSP

In terms of variables, there are fundamentally three sorts of constraints:

• Unary Constraints:
  These are the most basic types of constraints, limiting the value of a single variable.
• Binary Constraints:
  This is the type of constraint that connects two variables. A value x2 will have a value that falls between x1 and x3.
• Global Constraints:
  Global Constraints are the type of constraint that involves an arbitrary number of variables.

When it comes to natural language processing, there are four basic types of constraints which are - syntactic, semantic, discourse, and pragmatic.

• Syntactic Constraints:
  They are derived from the grammar of the language, for example, number agreement or word order
• Semantic Constraints:
  They are derived from the knowledge about entities that can exist in the world, for example, the properties that objects can possess like semantic features or selectional restrictions
• Discourse Constraints:
  These are derived from the structure of coherent discourse, for example, new entities in a sentence must be introduced first.
• Pragmatic Constraints:
  These are derived from the context in general; for example, the meaning of a sentence must be consistent with the social usage and speaker's goals: Can you pass the salt?

To learn more about each of these, you can refer to the independent scaler topics articles present on the topics.

Some particular sorts of solution algorithms are employed to solve the restrictions listed below:

• Linear constraints::
  These are often employed in linear programming, where any variable carrying an integer value exists solely in linear form.

• Non-linear Constraints:
  These are used in non-linear programming where each variable (an integer value) has a non-linear form.

Constraint Propagation

In local state spaces, there is just one option: search for a solution. However, with CSP, we have two options: We can either look for a solution or we can undertake a type of inference known as constraint propagation.

Constraint propagation is a sort of inference that aids in lowering the legal number of variables' values. The concept of constraint propagation is based on local consistency.

Variables are represented as nodes in local consistency, and each binary constraint is handled as an arc in the given issue. The following local consistencies are examined further below:

• Node Consistency::
  A single variable is said to be node consistent if all of the values in its domain satisfy the variables' unary constraints.
• Arc Consistency:
  A variable is arc consistent if all values inside its domain adhere to the variables' binary constraints.
• Path Consistency:
  When all of the binary criteria may be satisfied when evaluating a set of two variables concerning a third variable over another variable. Comparable to arc consistency
• k-Consistency:
  Stronger kinds of propagation are defined by the k-consistency type of consistency. Here, we look at a variable's k-consistency.

CSP Problems

Let’s take a look at some of the problems of constraint satisfaction. Keep in mind that constraint satisfaction problems are those that contain some constraints, limitations, or restrictions while solving the problem.

• Graph Coloring Problem:
  The graph coloring problem statement states that we need to color a graph such that no adjacent sides can have the same color. Here is constraint is that “no two adjacent sides can have the same color”.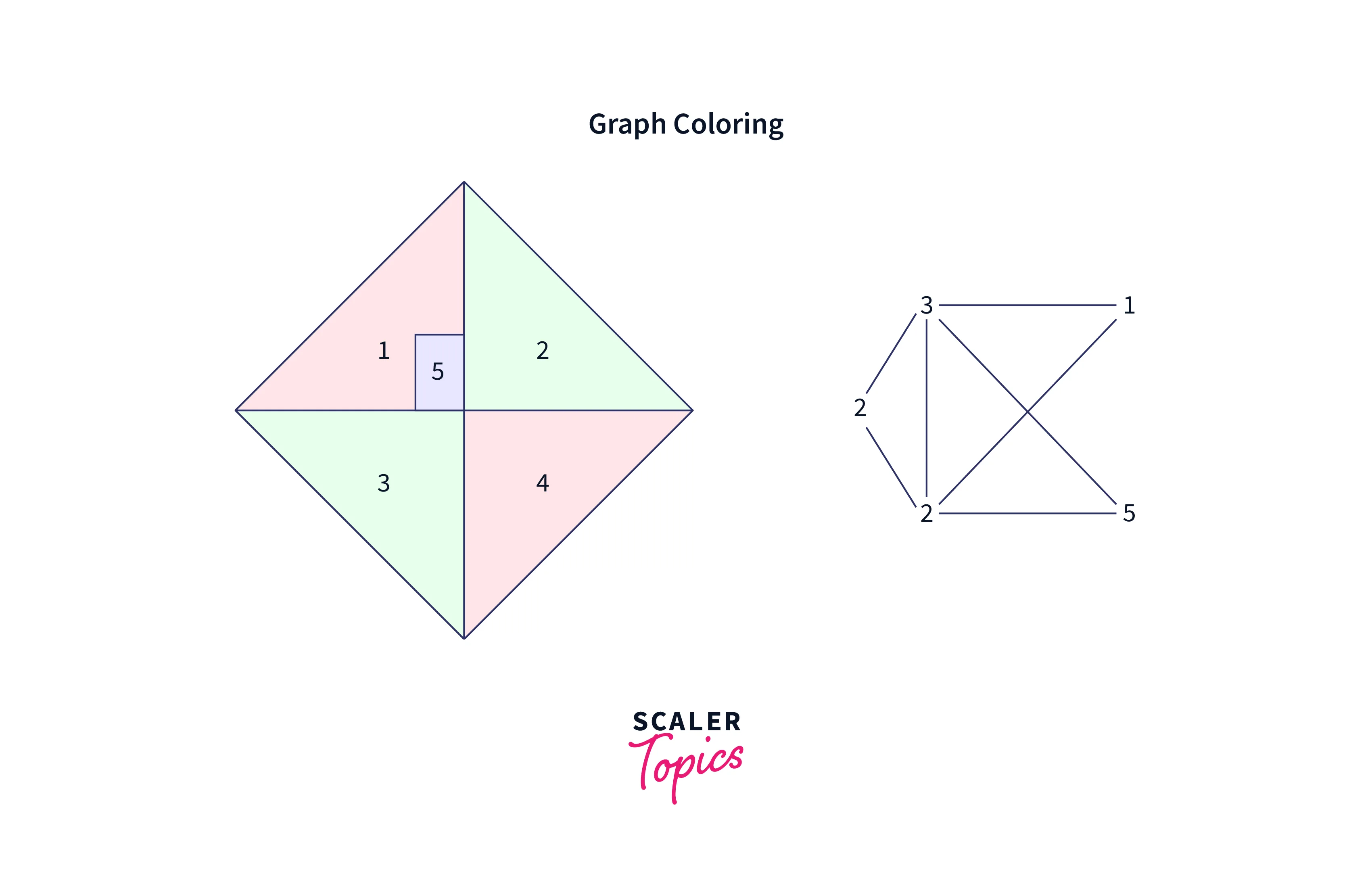

  

• Sudoku:
  As we discussed at the beginning of this article, sudoku is a classic constraint satisfaction problem. The task is to fill a number from $1-9$ in a box without repeating any number in a row or a column.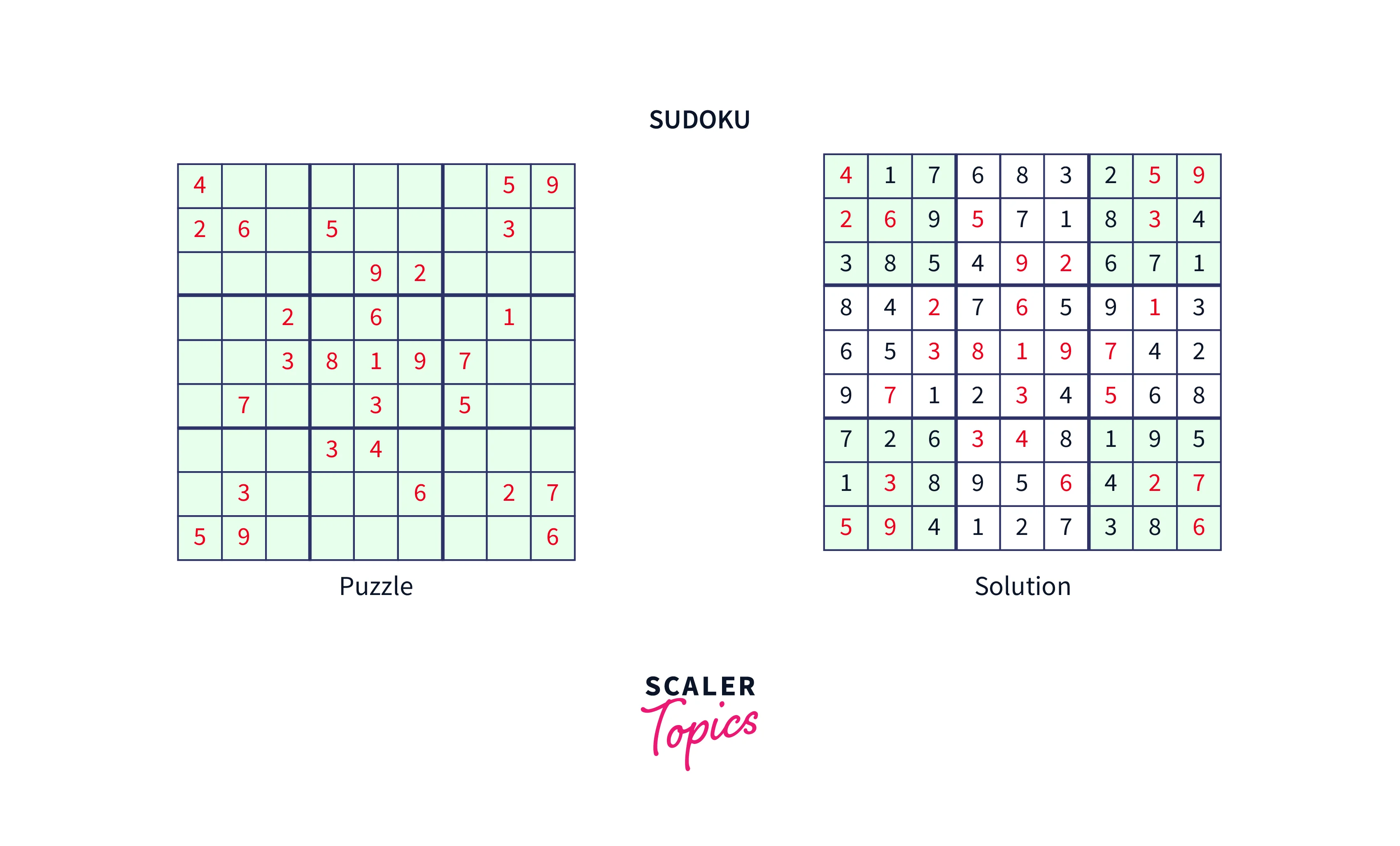

  

• N-Queens Problem:
  In the N-queens problem, the constraint is that on a chess board, no queen should be placed either diagonally, in the same row or column.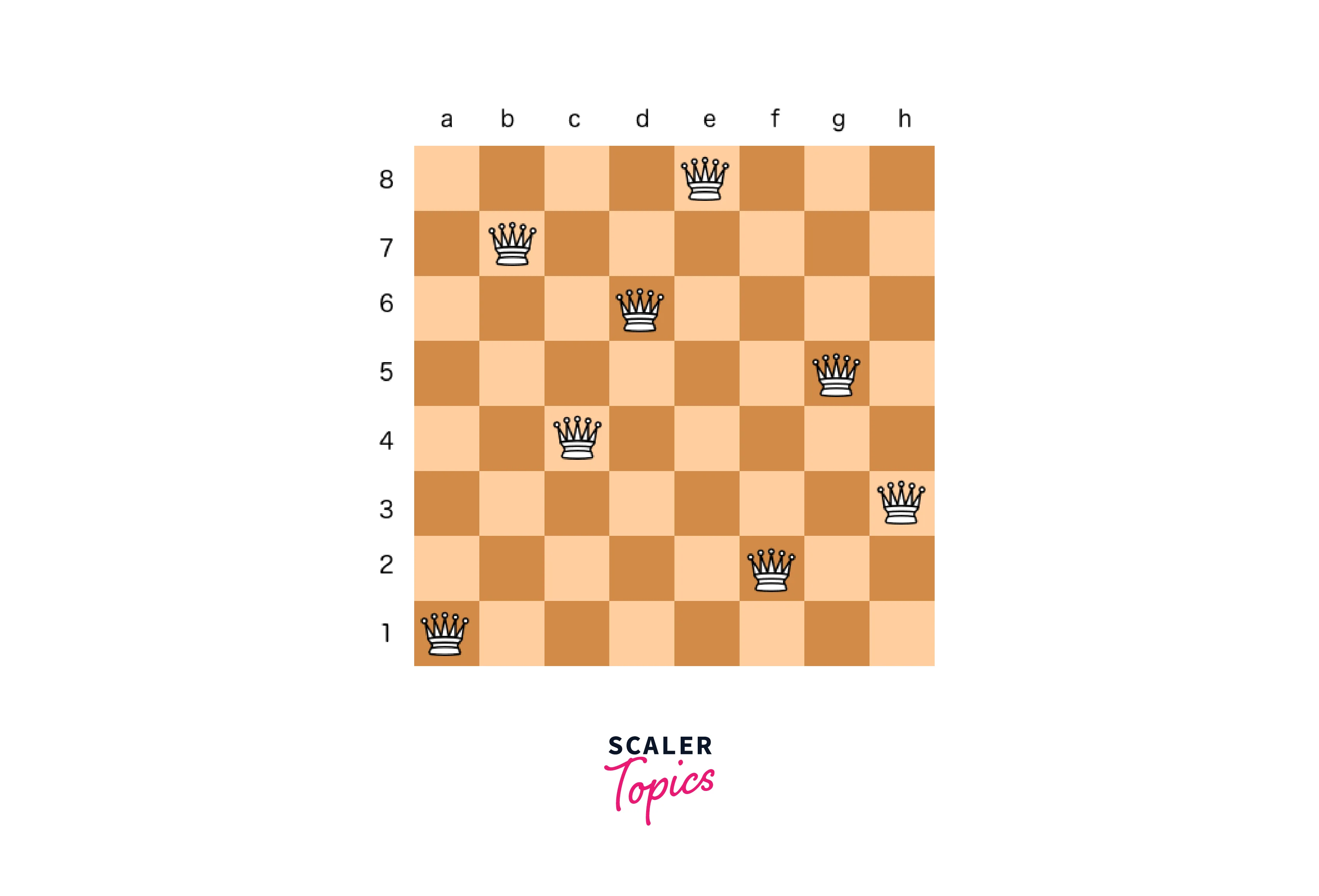

  

• The Crossword Problem:
  Crossword puzzle terms are treated as variables in the CSP with restrictions on them and one another. In other words, a word is a variable that must be a string of a specific length whose letters must match those of the intersecting word whenever it appears in a crossword. A variable x maintains a list of the other variables it intersects with and the points at which it does so, requiring that x's letters match those of the other variables.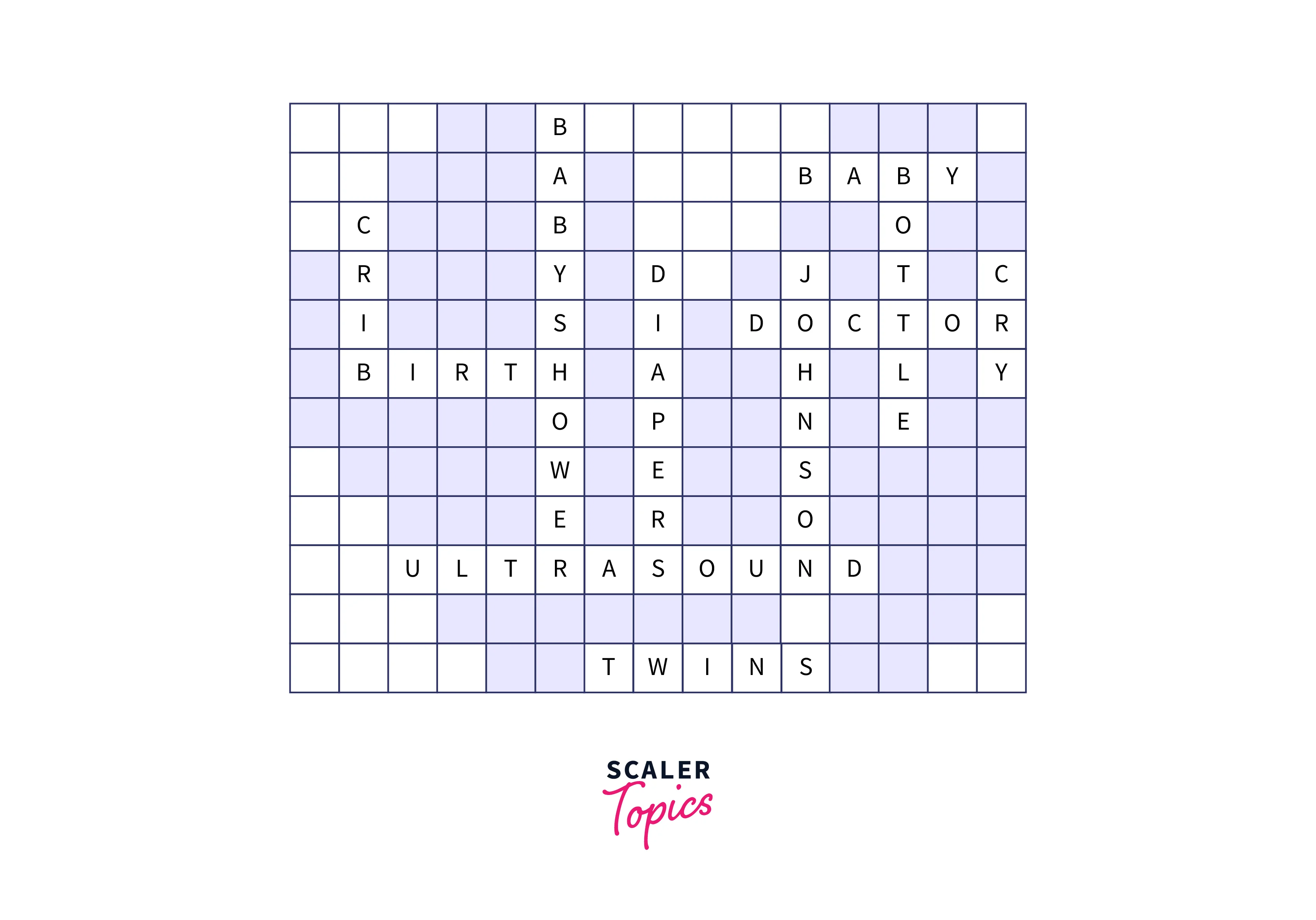

  

• The Latin Square Problem:
  A Latin Square is a $n x n$ grid with exactly one of each unique number in each row and column. We must produce a $n x n$ matrix of numbers from 1 to n that appear "exactly once in each row" and the column gave the input n. They may be shuffled but will contain the same digits.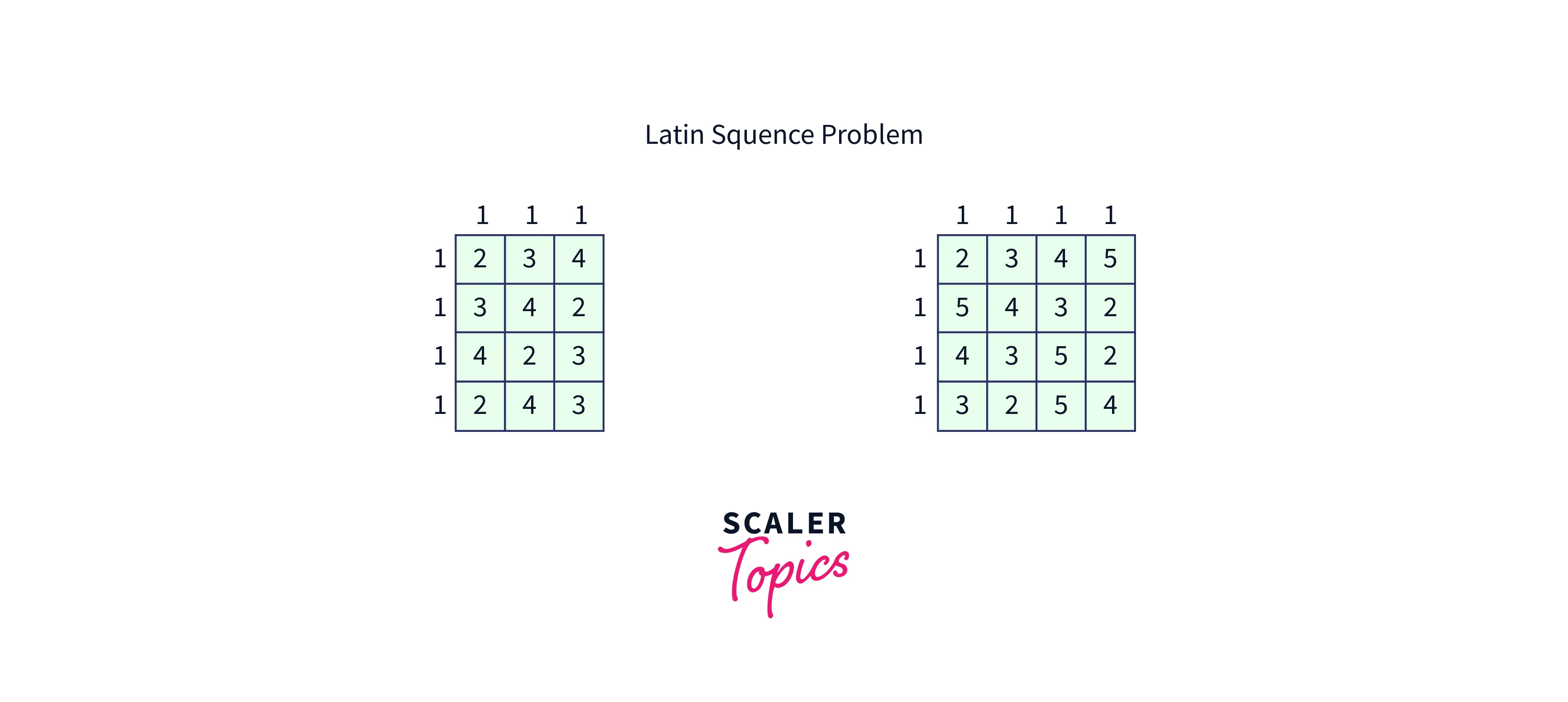

  

• The Cryptarithmetic Problem:
  A type of constraint satisfaction problem known as the cryptarithmetic problem involves replacing digits with unique symbols such as alphabets or other symbols. The digits (0–9) in a cryptarithmetic problem are replaced with potential alphabets or symbols.