Latent Dirichlet Allocation(LDA)

LDA Algorithm

Latent Dirichlet allocation (LDA) is an unsupervised algorithm with the aim of describing a set of observations in the dataset (preferably text) as a mixture of distinct topics or categories.

• The number of topics to be discovered is to be specified by the user to the algorithm.
• The topics are assumed to be shared by all the documents within the text corpus.

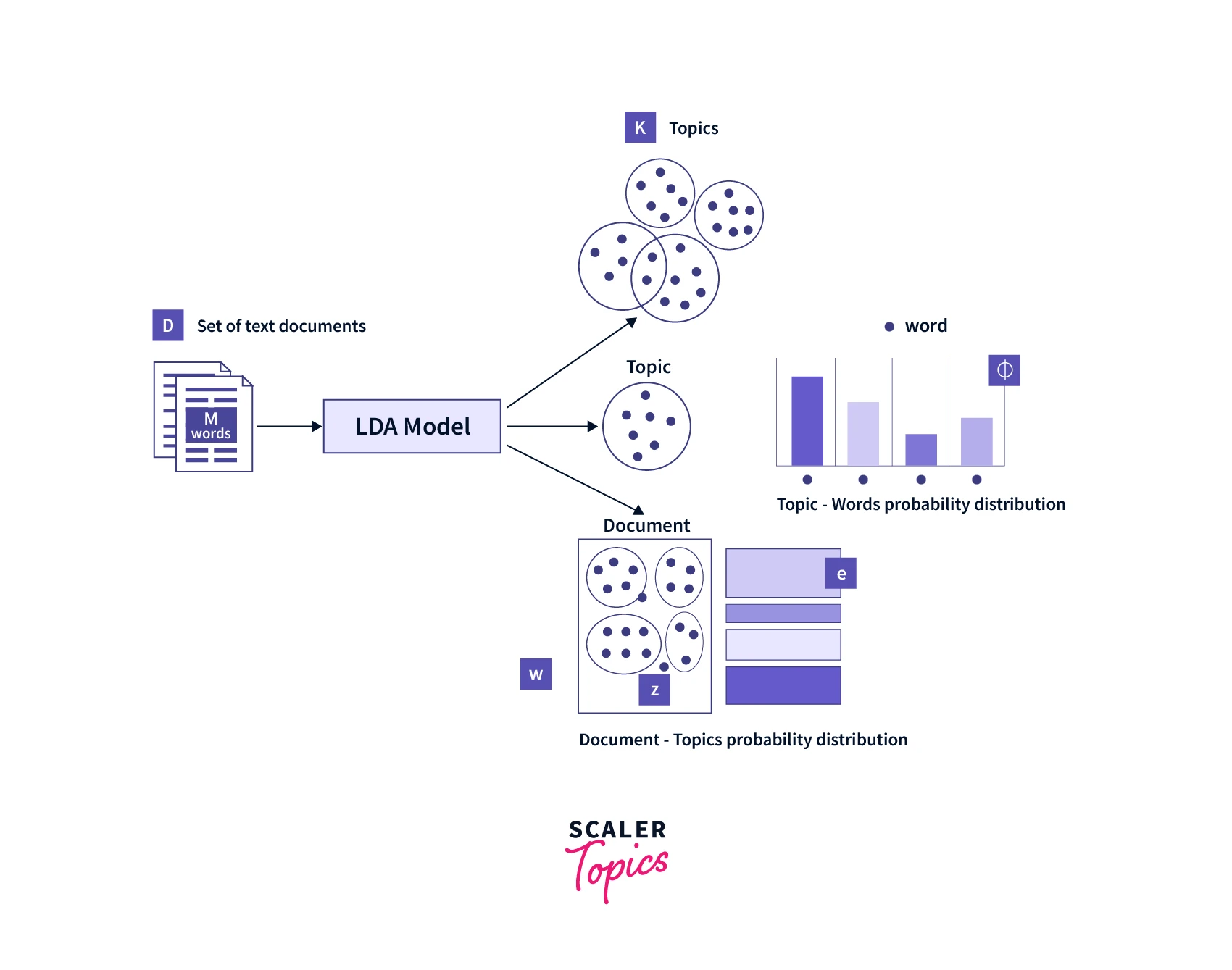
Explanation of different terms in the name of the LDA algorithm:

• The term latent in LDA signifies that documents are represented as random mixtures over some hidden (latent) topics, where each topic is characterized by a distribution over words.
• The term Dirichlet indicates the assumption that the distribution of these assumed topics and also the distribution of words in topics are both Dirichlet distributions.
• Allocation indicates the distribution of topics across the document in Latent Dirichlet Allocation.

Dirichlet Distributions encode the intuition that documents are related to a few topics. The main reason for dirichlet distributions is that it results in better disambiguation of words and a more precise assignment of documents to topics.

Latent Dirichlet Allocation Model

Dataset construction for LDA: Each document is treated as an observation and features for the model are constructed based on the presence of words (as counts or other suitable representations) over the entire text corpus. Each topic is also learned as a probability distribution over the features.

• We need to find the set of topics for each document.
• We also need to find all the words belonging to a particular topic.
• • Words are observed (from the dataset we have), and we need to learn/infer the topic, word distributions, and the hyperparameters for the model.

LDA works iteratively in the following steps:

• The initialization step in the Latent Dirichlet Allocation model is to randomly assign a topic (Z) to each word in each document.
• For each document and word combination, calculate the topic (θ) and word (β) distributions based on α and η:
  • p(topic_t | document_d): (Z_d,n) Words belonging to topic t in the current document excluding the current word
  • p(word_w| topic_t): (W_d,n) Words belong to the topic t for a given document d excluding the current word
• Then the calculated distributions are used to reassign the topics in the next cycle of iteration.
• This is repeated until converges of the algorithm. The training is run for some steps and all the distributions are learned.

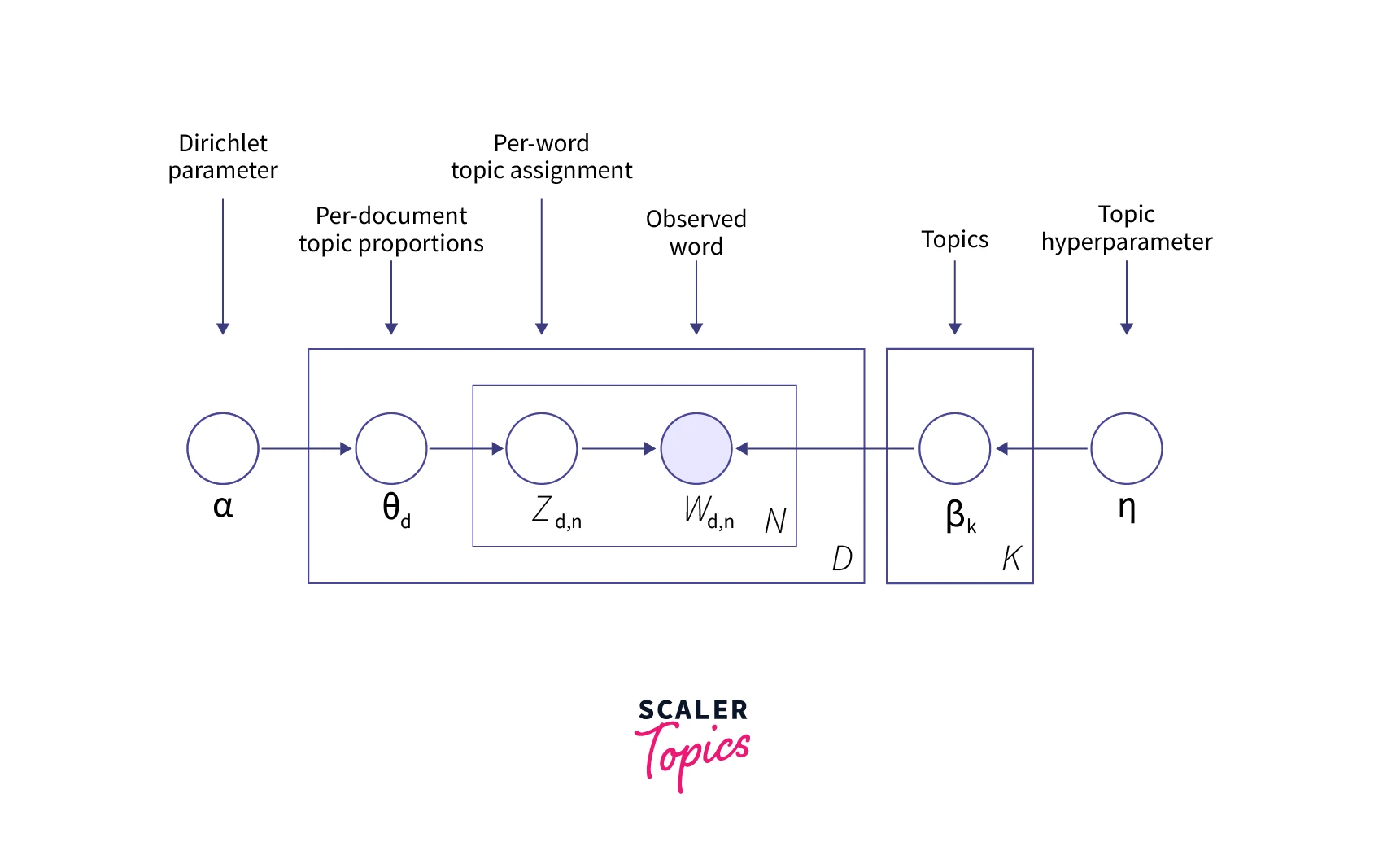
The iterative improvement in the assignment of topics to words is done generally through Gibbs sampling but there are also other approaches.

Finding Representative Words for a Topic

• After running the Latent Dirichlet Allocation model, we will get the scores for all input words (tokens) sent into the model for each topic. We can sort the words by the probability scores to get the order of importance.
• The top x (depends on problem statement and domain, like 10 for the top 10 words) words are chosen from each topic to represent the topic.
• If the corpus is small, we can store all the words for each topic sorted by their score.
• We can also set a threshold based on the score. All the words in a topic having a score above the threshold can be stored as its representative, in order of their scores.

How does Latent Dirichlet Allocation Work?

LDA works in two parts:

• Finding words that belong to a document, which is already seen from the corpus of documents.
• Finding the words that belong to a topic or the probability of words belonging to a topic, that are calculated from the Latent Dirichlet Allocation model.

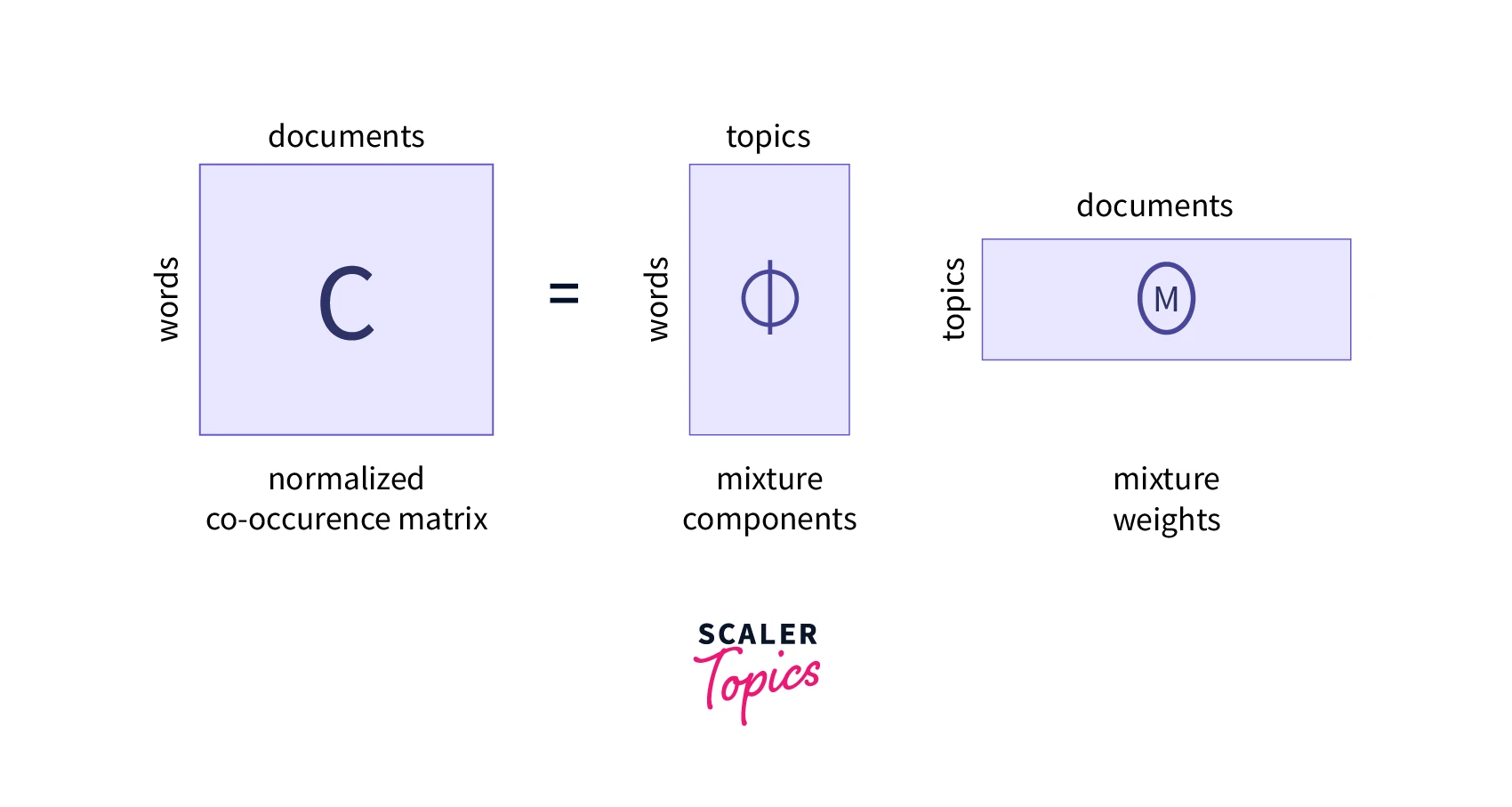
The exact content of two documents with similar topic mixtures may not be the same. We expect that the documents to more frequently use a shared subset of words, than when compared with a document from a different topic mixtures in general.

The above assumption in Latent Dirichlet Allocation to discover these word groups and use them to form topics.

Hyperparameters in Latent Dirichlet Allocation

• α: Document topic prior, is a prior estimate on topic probability, controls the number of topics expected in the document.
  • Low value of α is used to imply that fewer number of topics in the mix is expected and a higher value implies that one would expect the documents to have higher number topics in the mix.
  • Specifies the word distribution (the average frequency that each topic within a given document occurs).
• β: Topic-word prior, controls the distribution of words per topic.
  • Is a collection of k topics where each topic is given a probability distribution over the vocabulary used in a document corpus.
  • The topics will likely have fewer words at lower values of β and at higher values, topics will likely have more words.
• K: The number of topics to be discovered/considered.
• Ideally, we like to see a few topics in each document and few words in each of the topics, hence α and β are typically set below one while running Latent Dirichlet Allocation.

Coherence Score/ Topic Coherence Score

The coherence score is a measure of how interpretable the topics are to humans. It measures how similar words are to each other and a measure of how good a topic model is in generating coherent topics.

There are different metrics and it depends on number of topics and other hyper-parameters in Latent Dirichlet Allocation. We want to increase coherence score as much as possible while picking the model.

We can train different LDA models with different numbers of K values and compute the Coherence Score nd choose the value of K for which the coherence score is highest.

Data Preprocessing for Latent Dirichlet Allocation

Data cleaning is the main step for obtaining good results in the form of useful topic model for the latent dirichlet allocation model

• Tokenizing:

  Since words are the lowest level elements in LDA, we segment each document into all the words, which is called tokenizing to words

• Stop word removal:

  Some unimportant words like if, for, etc. which are ununcessary / meaningless are removed from the above token list.

• Stemming:

  This is to reduce topically similar words to their root. Helps in viewing similar terms as equivalent and improves their importance in the model.

Vectorization: This is done with bag of words implementation into a document term matrix which is the feature input into LDA.

Let us see an example of these steps in python using in-built libraries popularly used for topic modelling.

Some Real-World Novel Applications of LDA

• In recommender systems to find hidden relationships across users and items or for finding top items (aka topics) from the entire topics, like finding similar restaurants based on the menu or finding similar songs based on lyrics
• In the field of evolutionary biology and bio-informatics, LDA models are used to detect the presence of genetic variation in a different group of individuals.
• Latent Dirichlet Allocation is also often used to summarize the contents of large datasets. This is done by manually or automatically labeling the most popular topics produced by unlabeled LDA.
• The main application of LDA is in topic modeling for exploratory analysis and topic discovery.
• LDA is also applied in various fields such as software engineering, political science, medical and linguistic science, etc.