Radix Sort Algorithm in Data Structure (With Code in Python, C++, Java and C)

Radix Sort is a non-comparative algorithm that sorts the data in lexicographical (dictionary) order using Counting Sort as a subroutine. It is ideal for sorting integers digit by digit and strings character by character, it distributes elements into buckets by digit value, sorting repeatedly from least to most significant digit for final order.

Radix Sort Algorithm

In counting sort, we have seen that we can sort an array based on the frequency of elements in the array. But the only difficulty there was if the range of elements is very large then it's not efficient to use counting sort.

So we have come up with the Radix sort where we apply counting sort digit by digit from least-significant digit to most-significant digit.

Radix sort is a stable sorting method that uses counting sort as a subroutine. It is recommended to use radix sort on positive numbers only, however with some modification to standard radix sort algorithm we can also sort an array containing negative elements.

Steps Involved in Radix sort to sort an array in ascending order are --

Find the maximum element of the array, let it be $max$
Find the number of digits in $max$ , let it be $k$ .
For each, $i$ ranging from $1$ To $k$ , apply the counting sort algorithm for the $i^{th}$ least-significant digit of each element. If any element has less than $i$ digits consider $0$ at its place (Because $29$ can also be represented as $029$ ).

radix sort algorithm

Using this method you can also sort numbers that fit in 32/64-bit data types (int, float, double, etc) which was practically not possible with counting sort algorithm.

Note - If you haven't gone through Counting Sort yet, please have an eye on it once as it is a prerequisite for Radix Sort and if you want to sort an array in descending order, then tweak the counting sort function such that it sorts array in reverse order.

Example of Radix Sort Algorithm

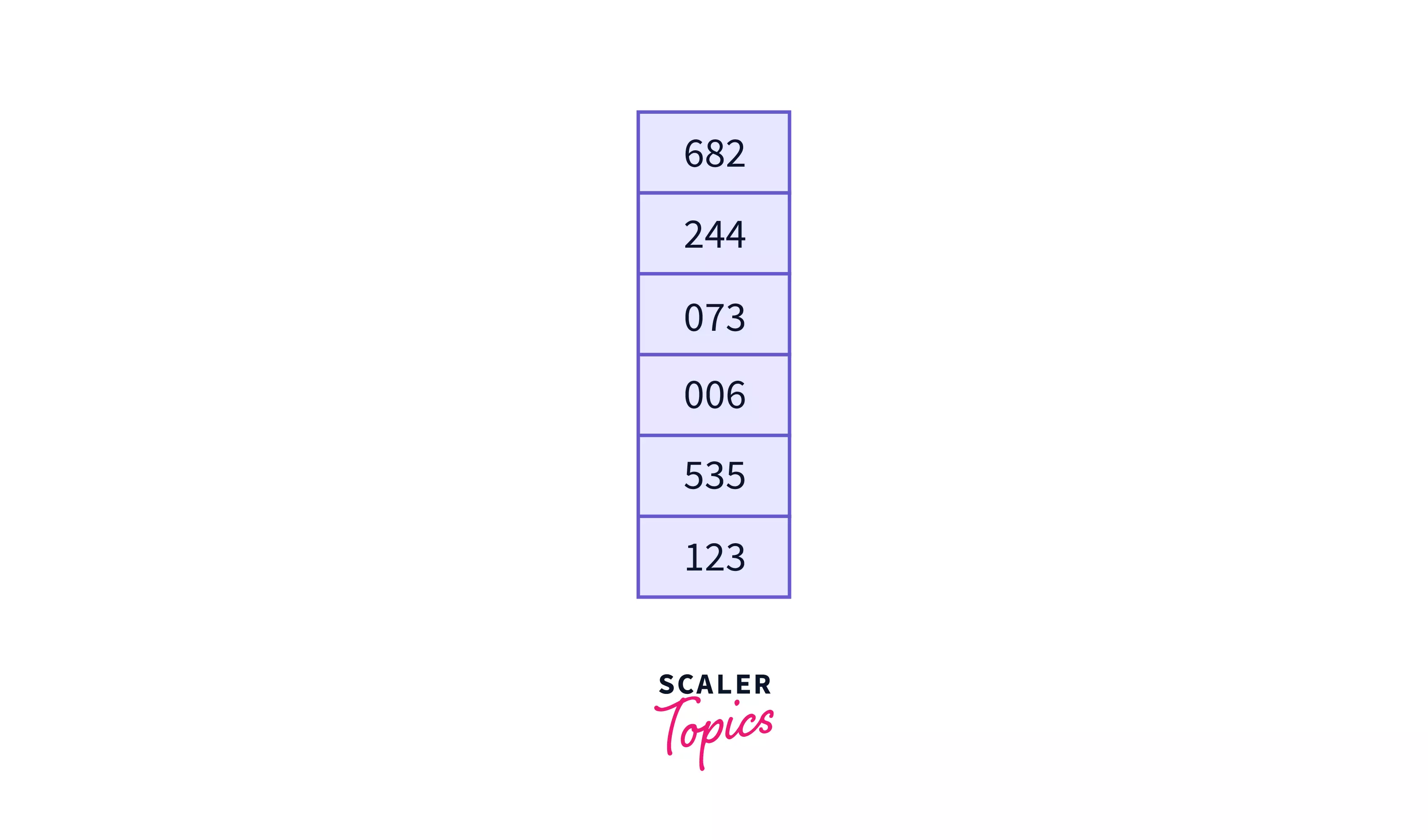
Let's assume we have an array $a=[682, 244, 73, 6, 535, 123]$ - example of radix sort algorithm

Here the maximum element is 682 which is of 3 digits, so we will apply the counting sort on the least significant digit $i.e.$ last digit -
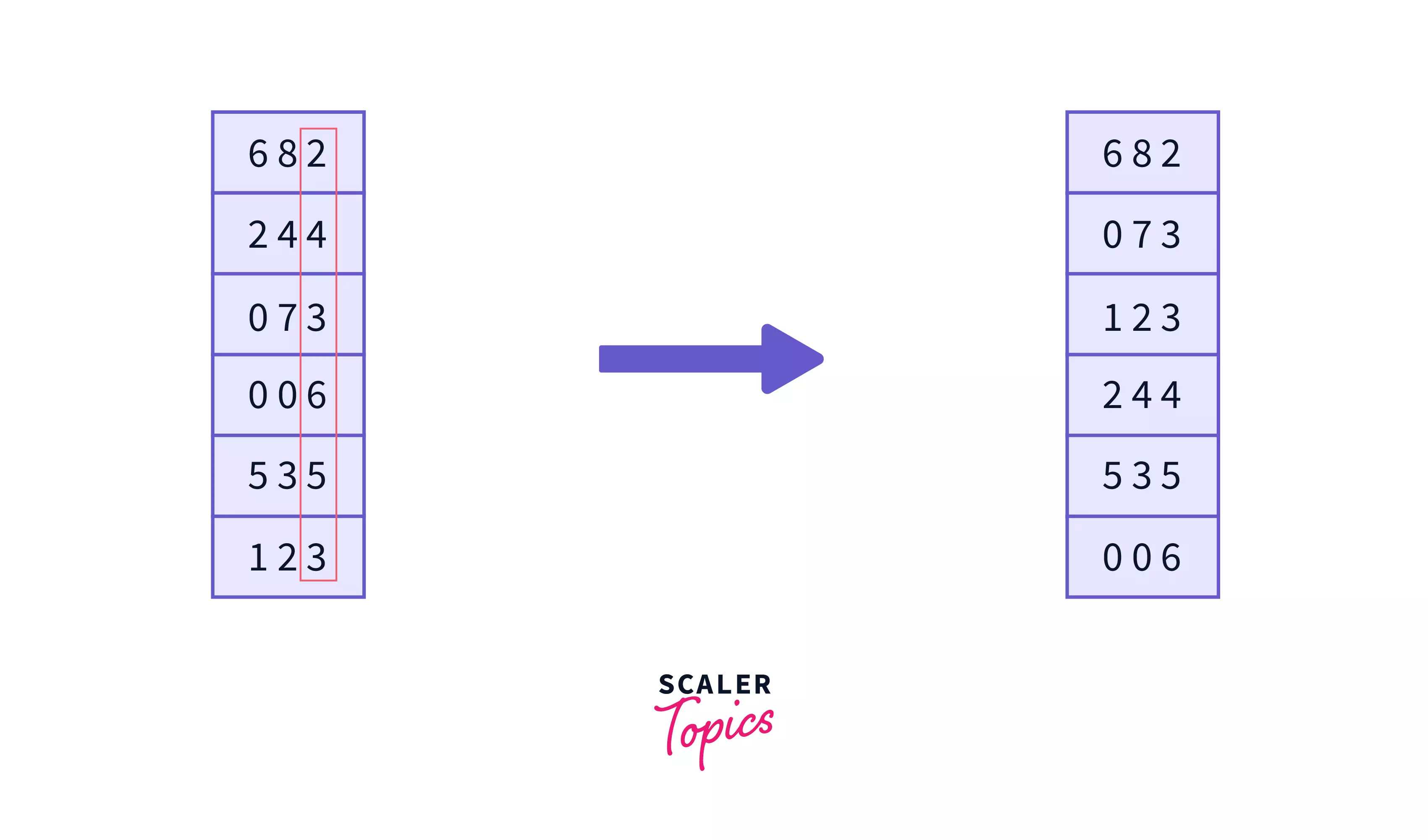
radix sort algorithm example

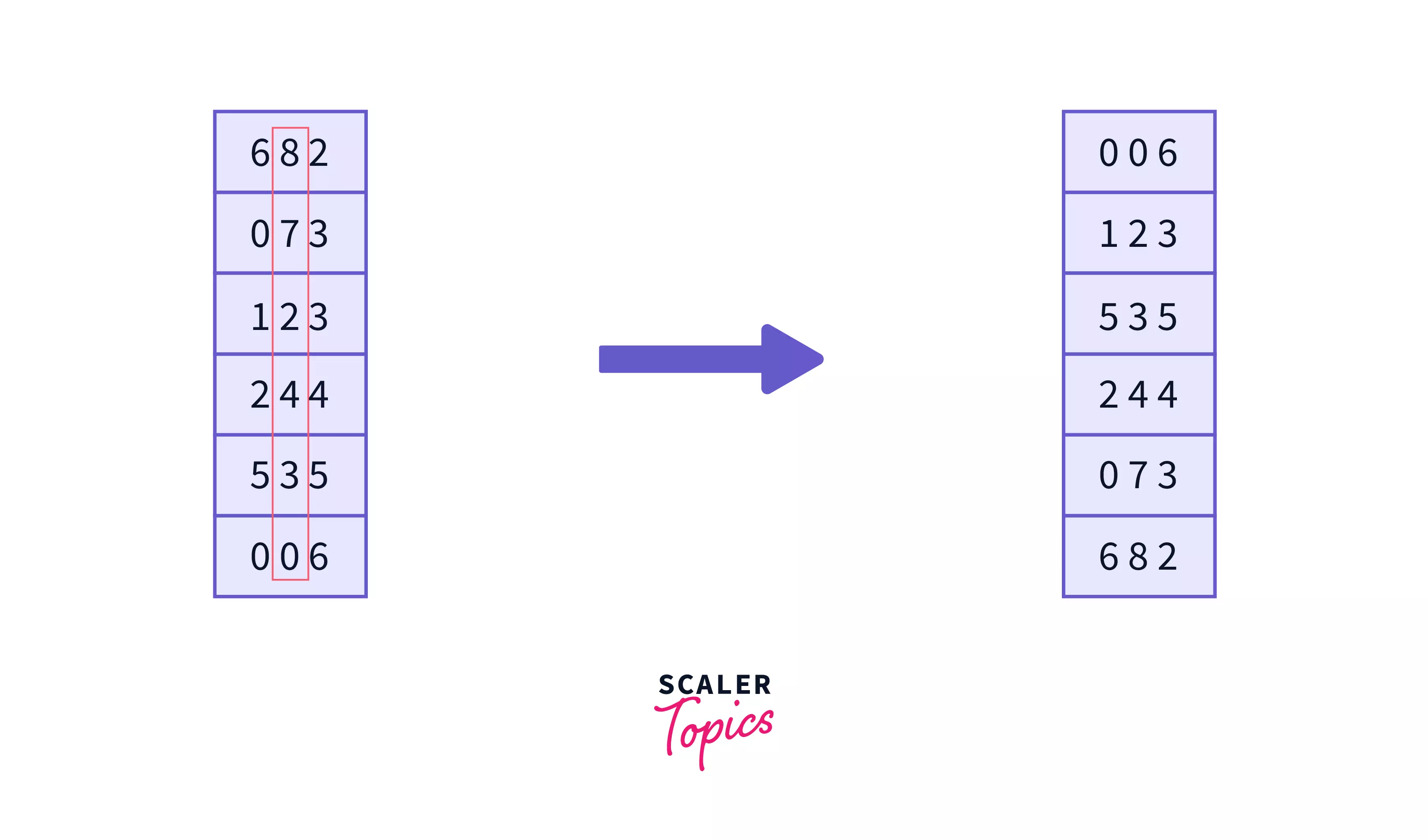
Now we apply counting sort on the second digit of the numbers, after which the numbers will get sorted on the basis of $2^{nd}$ least-significant digits - example radix sort

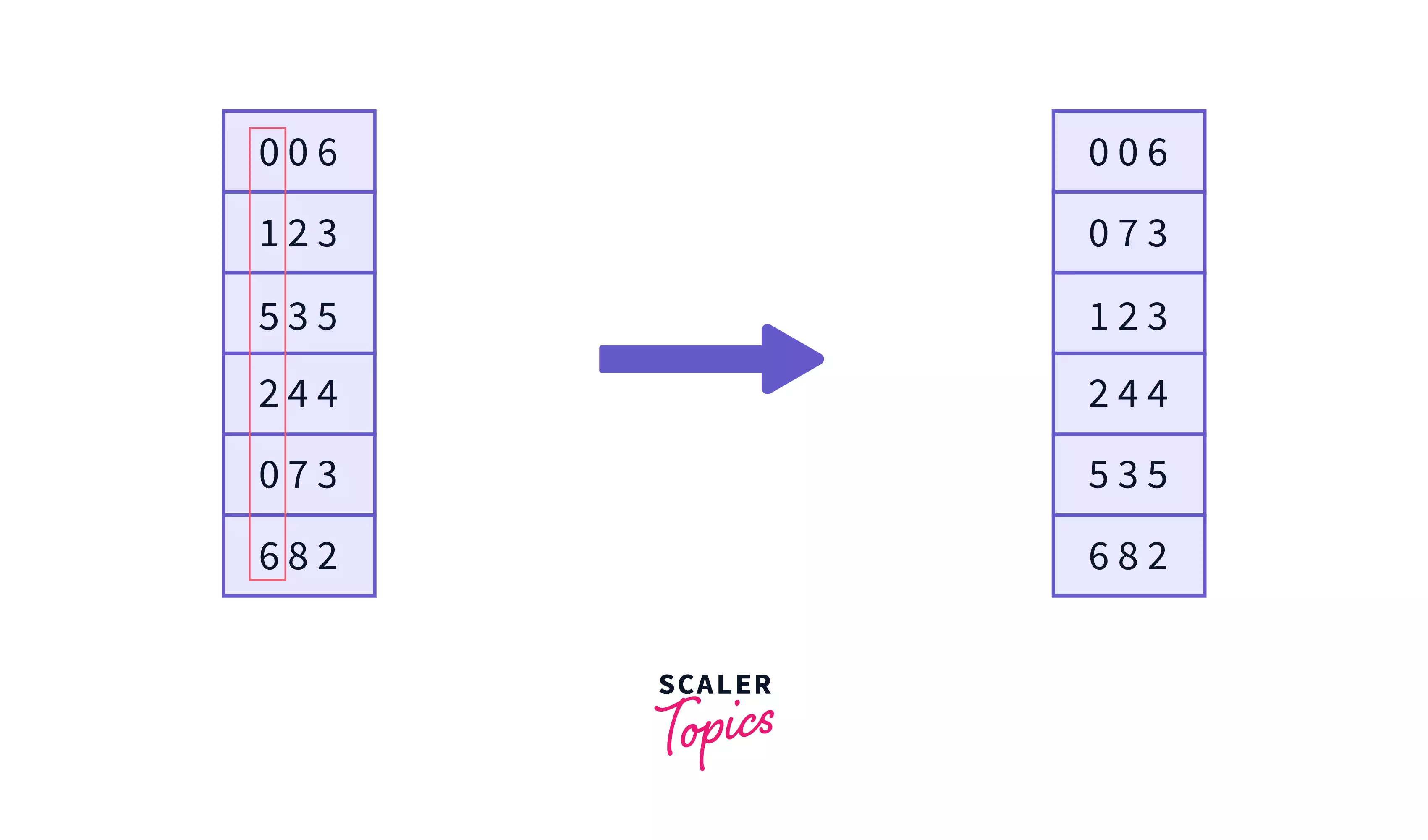
Now it's time to sort the numbers based on the $3^{rd}$ digit from right $i.e.$ the Most-significant digits. - radix sort example

And it's done, now the array is sorted in ascending order.

Pseudocode of the Radix Sort

In pseudocode, we will be having the function RadixSort which is the main function implementing the Radix sort functionality.

Firstly, the maximum element of the array is determined, then countingSort function is called $k$ times where $k$ is the number of digits in the maximum element found in the previous step.

Implementation of Radix Sort

For implementing the radix sort algorithm we will be using two functions -

radixSort - It takes an array (say $a$ ) and its size (say $n$ ) as arguments. Firstly, the maximum element ( $max$ ) present in $a$ is determined, then countingSort is called with a variable div till $max/div>0$ where $div$ is multiplied by $10$ after each iteration.
countingSort - It takes an array ( $a$ ), size ( $n$ ), and $div$ as arguments. Counting sort will sort the array based on the result obtained from $(a[i]/div)\%10$ . Where $(a[i]/div)\%10$ in each iteration corresponds to $k^{th}$ digit of $a[i]$ where $1\leq k\leq x$ .

Here $x$ denotes, the number of digits present in $max$ .

C/C++ Implementation of Radix Sort

Java Implementation of Radix Sort

Python Implementation of Radix Sort

C# Implementation of Radix Sort

Output - $1 \space 2 \space 4 \space 6 \space 9 \space 12 \space 21$

Complexity Analysis of Radix Sort

Radix Sort Time Complexity

Best Case - In the best case $i.e.$ when the array is already sorted, we do not need to apply the algorithm instead we can check if the array is sorted in a single traversal of the array. Hence time complexity is $O(n)$ in the best case.
Worst Case - In the worst case $i.e.$ array is sorted in reverse order, we need to apply the counting Sort (an $O(n)$ process) for $k$ times. Where $k$ is the number of digits present in the largest element present in $a$ .

Hence, the overall time complexity is $O(n\times k)$

Average Case - In the average case $i.e.$ elements of the array are arbitrarily arranged, again we need to apply counting sort on the array for $k$ times. Hence in the average case also, the time complexity is $O(n\times k)$ .

Radix Sort Space Complexity

Since we are using a $temp$ array in the Counting Sort process of size $n$ and a $count$ array of size $10$ the space complexity is $O(n+b)$ .

Where $b$ is the base of elements in the original array, since in the above case we are dealing with decimals (base 10), $b=10$ .

Applications of Radix Sort

It is highly beneficial to run the Radix sort on parallel machines, making the sorting process super-fast.
It is also used in constructing the suffix_array (An array that contains all possible suffixes of a string in sorted order.)

For example, If str="radix" then suffix array will be -

suf[0]="adix"
suf[1]="dix"
suf[2]="ix"
suf[3]="radix"
suf[4]="x"

Code with Confidence! Enroll in Our Online Data Structures Courses and Master Efficient Algorithms.

Conclusion

Radix sort is a non-comparison sorting algorithm that uses the counting sort algorithm in its implementation.
Other than integers, other data types like strings can also be sorted in lexicographical order using Radix sort.
The time complexity of the Radix sort is $O(n\times k)$ where $k$ is the number of digits present in the largest element of the array.

See More

Radix Sort Program in C